习题教学功能之拓展数学认识和题型见识

浙江海盐县三毛小学（314300） 何月丰

例题的主要功能是让学生通过解答问题来学习新的知识或技能。那么，例题能把小学数学中的知识与技能全部涵盖吗？答案是否定的。在小学数学中，例题教学的是最基础、最重要的知识与技能，还有基于例题的知识与技能而衍生出的相关的知识与技能，以及与此相关的一些题型，并没有被编设成例题，而是蕴含在习题中。由此，小学数学习题教学便承载了新的功能。

一、拓展学生对数学的认识

具体讨论习题教学在拓展学生对数学的认识这一功能之前，我们先来看一个案例。

案例1：异分母分数加减法

习题教学记：2019年5月27日，周一。

今天的数学课，我先反馈上一次作业的情况——学生在计算异分母分数加减法过程中出现的书写规范问题；在明确了格式上的规范性之后，再让学生以规范的格式写了两道习题，以加深印象，巩固技能；然后出示+这一异分母分数加减法的算式，要求学生观察后直接说出答案。在略作等待之后，一位学生站起来，犹犹豫豫地说出了。我板书答案后，让他解释是怎么想的。在确认学生的解释正确之后，我进行+的教学。

师：你们怎么越算越快了？（问题提出后，很多学生立刻举起了手）

生1：只要把分母乘一下，就是分母；分母加一下，就是分子。

师：把这个特点再观察、思考一下，为什么可以这样算呢？（学生静静地思考着，慢慢地，有学生举手了）

生2：因为这些分数的分母是互质数，所以分母就是它们的乘积，分子就是交叉相乘，这样加一下就可以了。

这位学生的解释显然是正确的，只是表述含糊不清。于是，我再请一位学生表达自己的想法。最后，我以+为例，结合板书，与学生一起再次理解其中的算理+=+==。

第一步：通分。原来分数的分母互质，分母相乘做分母；原来分数的分子都是1，分母成了通分后分数的分子。

第二步：相加。和的分母相当于原来分数的分母相乘，和的分子相当于原来分数的分母相加。

……

以人教版数学教材为例，在案例1 涉及的五年级“分数加减法”这一教学内容中，教材一共编排了4 道例题，分别是“同分母分数加减法”的例1、“异分母分数加减法”的例1 以及“分数加减混合运算”的例1、例2。这4 道例题都不涉及案例1 中所发现的知识，与此相关的“发现”出现在“异分母分数加减法”教学之后的练习二十四第6题中（见图1）。

图1 人教版数学教材五年级下册练习二十四第6题

类似于上述将某一数学知识蕴含在习题教学中的情况，在小学数学教学中是非常常见的。如学习平行四边形、三角形的面积计算之后，教材会在后续的习题教学中引导学生发现“等底等高”的相关知识。由此可见，习题教学具有拓展学生数学认识的功能。这也正如波利亚所言：“一个重大的发现可以解决一道重大的题目，但是在解答任何一道题目的过程中都会有点滴的发现。”因此，作为一名小学数学教师，要善于理解和挖掘习题的内涵，精心设计习题的教学过程，带领学生在解答习题的过程中去进一步发现，拓展学生的数学认知。

这个时候，我们自然会有这样一个疑问：“为什么这样的数学知识、技能不编排成例题呢？”原因是多方面的，以下两点可以作为对此问题的回答。

第一，突出例题的代表性，控制例题数量。

例题中承载的知识或技能，往往是某一知识或技能的源点。通过这个源点，可以衍生出很多支流。在从源点衍生出的这些支流中，一些基础的、重要的代表性支流中蕴含的知识或技能则可以再次编排成例题。如学习“乘法分配律”之后，应用乘法分配律进行简便计算，一般有7 种典型题型（见表1）。

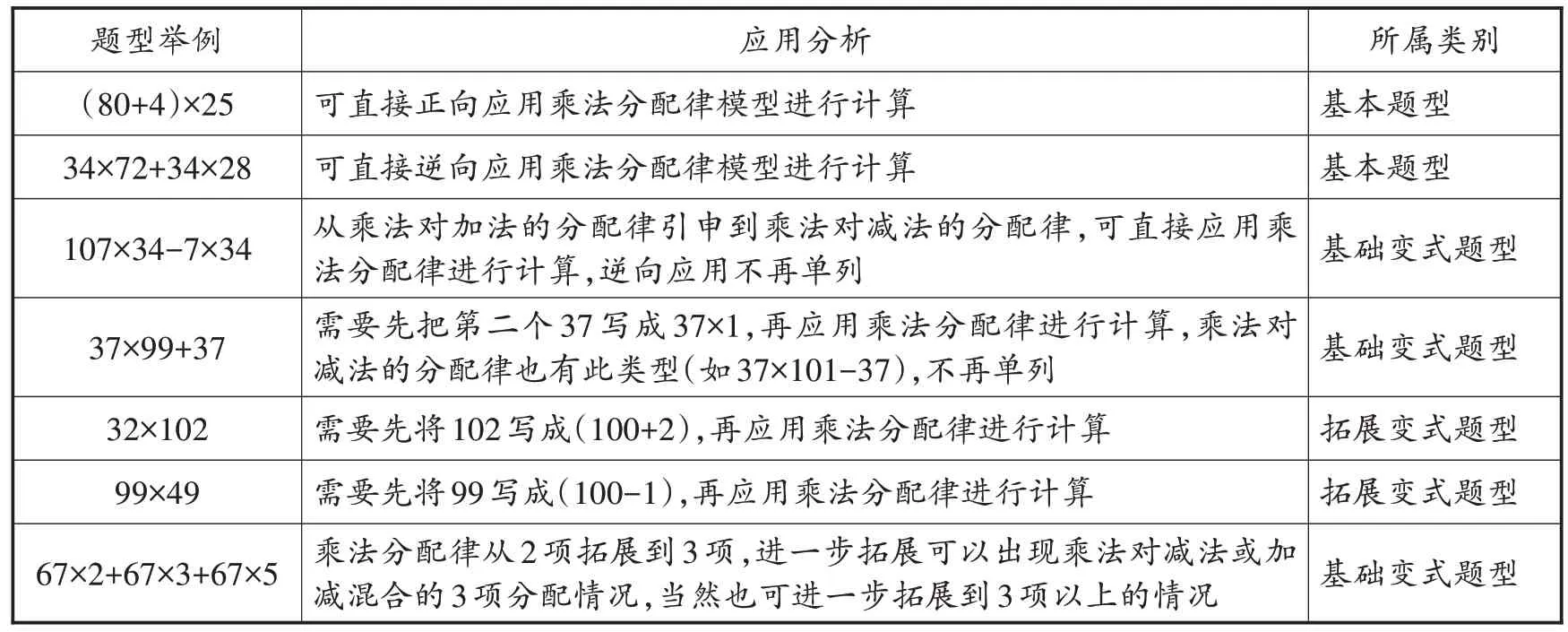
表1 乘法分配律简便计算的典型题型分析表

对小学数学7 个版本的教材进行统计分析后发现，没有一个版本的教材将表1 中的7 种典型题型都编排为例题（见表2）。一方面，通过表2 可以发现，在乘法分配律的7 种典型题型中，例题编排率最高的是“34×72+34×28”型，有6 个版本的教材编排了；例题编排率位于第二的是“（80+4）×25”型，有5 个版本的教材编排了；例题编排率位于第三的是“32×102”型，有3 个版本的教材编排了。可见，这3 种题型是具有代表性的。其中，“34×72+34×28”型和“（80+4）×25”型的代表性体现在其基础性上，即这2 种题型是乘法分配律这个源点衍生出去的主干支流，因此编排为例题的必要性最高；而“32×102”型的代表性体现在其拓展性上，是具有代表性的一种典型题型，所以也有编排为例题的必要性。至于“107×34-7×34”型，虽然蕴含了乘法对减法的分配律这一新知识，具有拓展、完善学生对乘法分配律认识的功能，但因为这一知识只要基于乘法对加法的分配律的意义，就容易从“34×72+34×28”型中实现思维的正向迁移，因此不具有代表性，故7 个版本的数学教材将这种题型均编排在习题中，而不编排为例题。至于“37×99+37”型和“99×49”型，同样只要在习题中将例题知识实现迁移即可。

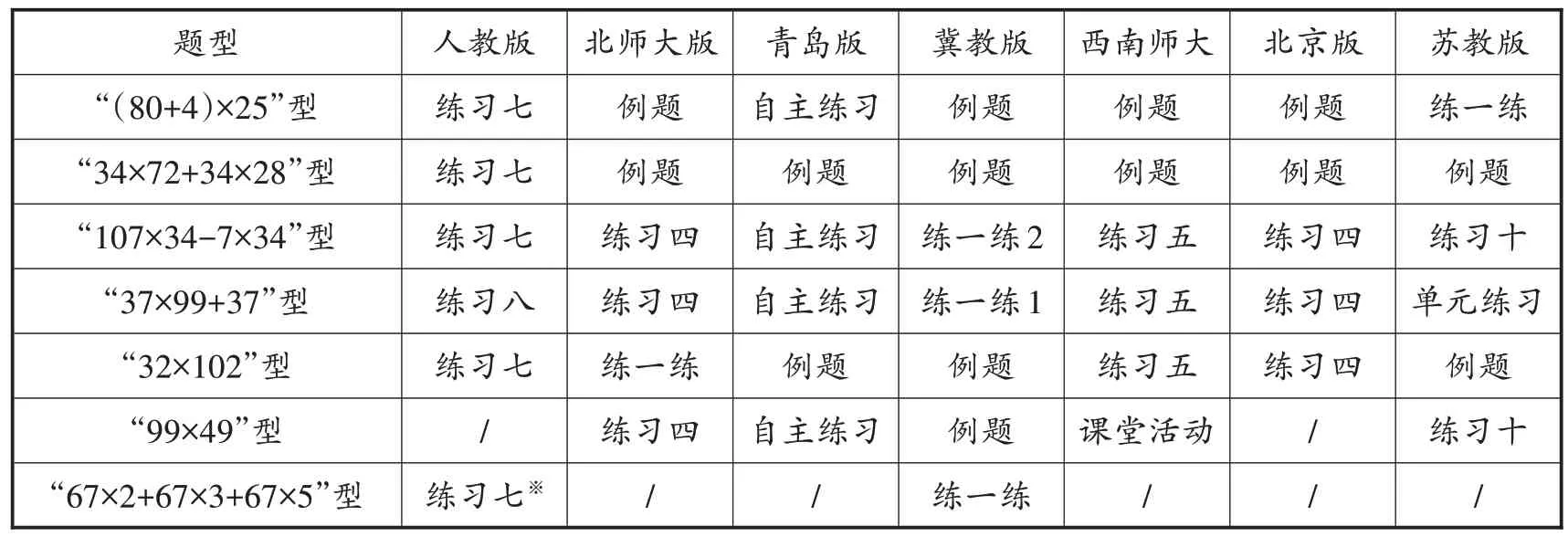
表2 乘法分配律典型题型在各版本数学教材中的编排情况统计表

另一方面，如果把这些支流都编排为例题的话，那么教材上的例题会有很多，数学教材就会很厚，这显然是不合适的。因此，只要将具有代表性的支流编排为例题即可，与此有一定关系的知识或技能，可在习题教学中让学生进行迁移学习，这也是提升学生应用能力、创造性解决问题能力的一个重要途径。

第二，知识点是一种拓展性认识，非“双基”。

2023 年春季，人教社数学1～6 年级下册全新插图版教材正式使用。这套新插图版教材除了插图全部重绘，对部分内容的编排也进行了调整。如四年级下册“小数的意义”单元，在学习了“小数点移动”之后，旧插图版教材中编排了一道解决问题的例题（见图2），并在这道例题之后的练习十一中编排了4 道对应的解决问题习题。而在新插图版教材中，图2 这道解决问题的例题被删除了，同时删除的还有练习十一中4道解决问题的习题。

图2 人教版（旧插图版）数学教材四年级下册“小数点移动”解决问题的例题

这在一定程度上反映出教材在例题与习题编排上的一个要求：数学教材中，编排为例题的知识或技能，一定是“双基”的重要组成部分。但是，出现在习题中的数学知识或技能可以不是“双基”，而是作为一种对例题知识学习之后的拓展性认识。如在上面的例子中，图2 作为例题出现，那么这个知识就是“双基”，是要求所有学生都要掌握的，为此就有专门的习题用于练习巩固。而在案例1 中提到的异分母分数加减法的计算方法，因为出现在习题中，故不要求所有学生都要学会，理由是这种计算方法只是针对异分母分数加减法中的一类特殊题型才适用的简便算法而已，这种计算方法学生会不会与能不能正确计算异分母分数加减法没有关系。因此，这只是作为异分母分数加减法中的一种拓展性知识来认识，不是“双基”。由此可见，类似于案例1 中的拓展性知识，适合出现在习题中，而不适合编排为例题。

二、拓展学生对习题题型的见识

有一定教学经验的小学数学教师在针对某一知识的习题教学中，会在合适的时机针对这一知识安排一些特定的习题题型。甚至有时候会有这样一种感觉，如果在教学这一知识时没有安排这种特定的习题题型，就会觉得这一知识没有教学完整，学生难以理解与掌握这一知识。

案例2：除数是一位数的除法

习题教学记：2020年4月28日，周二。

课件出示习题：□63÷8，如果商末尾有0，那么□里可以填（ ）。

师：怎样才能使商末尾有0？（学生被这个问题难住了，略作等待之后，一位学生犹豫着举手了）

生1：就是最后比除数小。

我理解这位学生的意思，但估计现在只有自己才是他的知音，其他学生肯定是一头雾水。

师：也就是个位除不动，是不是这个意思？（生1点点头）这到底是什么意思呢？我们来试试看。

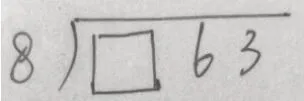
我板书了如上的除法竖式，从最小的数开始，填入1试一试，得到下图。

师：观察一下，看明白了什么？

生2：最后的3比除数小。

此时，我知道有些学生对生1的说法有点理解了。于是，我和学生再一起边看竖式边理解。

师：对呀，将最后个位的数移下来，商不够1，就只能是0了。这样，商的末尾就有0了。

我把竖式写完整，让学生直观地看到商末尾的0。但感觉这样教学，还是不痛不痒，不是滋味，需要继续观察思考。

师：怎样才能使个位上的数移下来还是不够除呢？

很快就有学生举手了，我知道这个时候学生对这道习题开始有点感觉了。于是，我依旧等待，等待更多的学生举手。

生3：前面正好减去，没有余数。

（这是很了不起的一步，但我装作若无其事的样子）

师：说说简单，怎样才能使前面正好减去而没有余数呢？

学生先独立思考，再同桌讨论，最后全班一起交流，最终发现：只要8的乘法口诀中得数个位是6的情况就可以。于是，学生又想到了□中可以填5，这样商是70，末尾有0，并填入2 和6 验证是不行的。

从回答的情况看，学生填入1 和5 的情况比较多，当然两个都填入的极少。不过，明眼人一定已经看到，这道习题还有一个答案——9。为什么学生能想到1和5，却想不到9呢？因为8的乘法口诀中没有得数是96的。

师：看来，这里可以填1，也可以填5。还有不一样的答案吗？（学生表示没有了）我告诉大家，还有一个答案。（等待，等待……终于，一位学生举手了）

生4：9。（学生自己尝试，发现9是正确的）

在完成9 的验证之后，学生进一步讨论：为什么我们都想不到9？

……

案例2 中的习题“□63÷8，如果商末尾有0，那么□里可以填（ ）”，相信教过“除数是一位数的除法”这一知识的教师一定不会陌生，因为这是习题中的一种经典题型。因此，当教学这一知识时，很多教师都会安排这样的特定题型让学生练习。这种题型后续还会出现在很多相关知识的习题中，如“除数是两位数的除法”等。

计算教学的一个很重要目标，就是使学生能够正确、灵活地进行计算。但是，类似案例2 这样的习题不是为了获得一个正确的计算结果，而是为了巩固学生对算理的理解和掌握，因此这种题型也会经常出现在检测题中。这就是说，有时候为了检测学生对某一数学知识是否全面、深入地理解和掌握，经常会有一些与这一目标相匹配的特定题型出现。经过长时间的发展，其中有一些特定题型已经成为经典题型。这种经典题型有时出现在例题中，有时则出现在习题中。

类似于这样的经典题型，在小学数学习题教学中是很常见的。

“小数的意义”中的习题：一个两位小数，保留一位小数后是2.6。这个两位小数最大是（ ），最小是（ ）。

“分数的意义”中的习题：把一根5 米长的绳子平均分成9段，每段长（ ）米，每段占全长的（ ）。

“圆的面积”中的习题：一块草地上有一根木桩，上面用一根4 米长的绳子拴着一只羊。这只羊最多能吃到草的面积是多少平方米？

上面三道习题，都是相对应知识习题中的经典题型，甚至像“小数的意义”和“分数的意义”中的习题，已经成为这些知识习题教学中的易错题型。因此，像这样的经典题型，如果在习题教学时没有让学生见识过，估计没有一位教师心里是踏实的，因为这不仅关系到学生对相对应知识的理解和掌握，还关系学生的检测成绩。

由此可见，小学数学习题教学具有拓展学生对习题题型见识的功能。当然，这种见识不是仅仅见过这样的习题，更是理解和掌握这些习题的解题策略。

在习题教学中拓展学生对习题题型的见识，一方面体现在上述提到的经典习题上；另一方面，体现在习题的变式上（见图3）。

图3 人教版数学教材四年级上册解决问题的习题

这是人教版数学教材四年级上册“除数是两位数的除法”单元“整理与复习”中的一道习题，其特点是首次出现了“买3棵送1棵”这样购物问题中经典的“买几送几”的信息。因此，对于使用人教版数学教材的学生而言，面对这道习题是一种新的题型见识。教学中，通过直观演示、图示表征等方式，学生能较好地理解其中“买3 棵送1 棵”的意思，进而理解这道习题的解答方法。

但是，这道习题的教学到此还远没有结束。请看图4，在与这节课配套的本地《课堂作业本》（浙江教育出版社，浙江省厅教研室组织编写）中连续出现了这道习题的两次变式。

图4 《课堂作业本》中的两道变式题

变式一：增加了一个比较单价的问题。

变式二：将原本告知“总价”的条件变成告知“数量”的条件，问题也随之发生变化。

因此，在教学这道习题时，绝不能仅仅满足于这道习题本身，而要着眼于这道习题可能存在的变式，进一步拓展学生对题型的见识。类似于这样的情况在小学数学习题教学中很常见，我们不妨再来看其他的例子。

一位有经验的教师，会在教学经典习题后，教学变式习题；一位新手教师，则可能不会教学变式习题。因此，不管是从学生对知识、习题的理解和掌握来看，还是从最后的学科检测成绩来看，帮助学生拓展题型见识往往成了新手教师在教学质量上败给有经验教师的重要原因。所以，学生数学学习的疑难点，一般不是表现在数学知识和技能本身，而是表现在运用数学知识和技能解答某一类型的习题上。有没有让学生见识过多样的、特别是经典的习题，对学生的数学学习非常重要。

综上所述，小学数学习题教学具有拓展学生数学认识和习题题型见识的重要功能。