基于规划模型的运输网络最大流问题的分析研究

晏榆洋 张浩 帅培

摘 要：当今，世界经济形成命运共同体，各国各地的贸易往来非常频繁。物流产业作为供应链的重要组成部分，也迎来快速发展。研究运输网络最大流问题成为许多学者关注的焦点。现实生产生活中，某地区有一公司需将货物从配送中心运送至仓库储存，在运输过程中，物流车会遇到若干个路口，因为每段路程的车辆承载量和目前平均通过量各有不同，因此，文章通过建立规划建模求解，得出货物运输效率最大的研究结果，以期在实际物流运输环节中节约大量的成本。

关键词：供应链；网络最大流；线性规划模型；方案研究

中图分类号：F275；U491文献标志码：ADOI：10.13714/j.cnki.1002-3100.2024.08.002

Abstract： Today， the world economy is a community of shared future， and trade between countries and regions is very frequent. As an important part of the supply chain， the logistics industry has also ushered in rapid development. Research on the maximum flow problem of transportation networks has become a problem for many scholars to study. In real life， a company in a certain region needs to transport goods from the distribution center to the warehouse for storage. During the transportation process， the logistics vehicle will encounter several intersections. Because the vehicle capacity and current average throughput of each section of the road are different， this article establishes a planning modeling solution to obtain the research result of maximizing the efficiency of goods transportation， which can save a lot of costs in practical logistics transportation.

Key words： supply chain; network maximum flow; linear programming model; program research

1    问题背景

在日常生活中，许许多多的系统都涉及到流量问题。例如，运输系统中有车辆流量，供水系统中有水流量，控制系统中有信息流量，金融系統中有现金流量等。网络流量是指在指定的时间段内通过道路某一地点或某一车道的实体数量。网络最大流问题是一种组合最优化问题，就是要讨论如何充分利用现有资源，使运输的流量最大，达到最佳的效果。在交通网络系统中，路段或道路可以用边来刻画，流量就是路段的车流量，容量就是路段可承受的最大车流量。网络最大流问题就是求从配送中心可以发多少车辆，同时还要不超过任何一条车辆途经路段的容量限制，而且每个节点的进出流量守恒。学者张丰等[1]研究解决了无环路的网络最大流问题，给出一种运用最小截原理来求解的图上作业法及该算法的理论依据与证明，并通过举例说明该算法的简便性与有效性。该算法能直观地求出最大流和最小截，比使用教材上提到的其他方法节省大量计算时间。郭鑫龙[2]研究如何在这些限制条件下，尽可能地提高对网络的利用率，减小资源消耗，通过对几种最大流算法进行介绍，并分析比较各自性能，以便在特定的应用环境下选用合适的网络最大流算法来解决相应的问题。谢凡荣[3]为了便于建立与网络最大流问题有关的决策支持系统，给出一个求解网络最大流问题的数值算法，证明算法的理论依据，并举例说明算法的应用。该算法能求出网络最大流和最小截，并具有易于编程、收敛性好等优点，大量数值实验表明该算法非常实用有效。张超等[4]给了一个基于Ford-Fulkerson算法求最大流的思路，对有流量需求的分品种容量限制的运输网络构造最大流算法，将有流量需求的转运节点分为转运节点和汇节点，同时构建单源单汇，寻找增流链进行流量调整。同时，通过示例对算法进行验证，计算满足流量需求和分品种容量限制的运输网络的最大流。

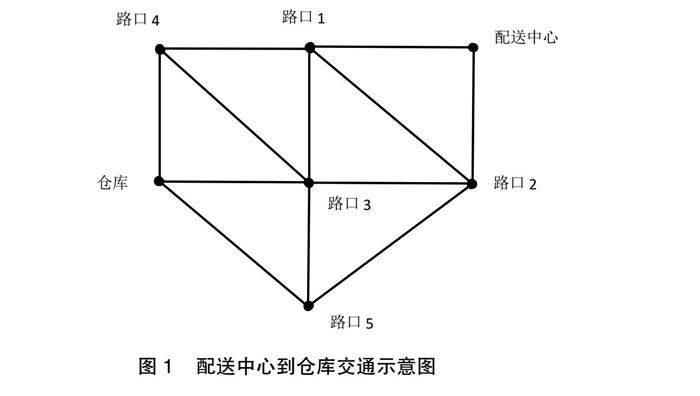
现实生产生活中，某地区有一公司需要将货物从配送中心运送至仓库储存，在运输过程中，物流车会遇到若干个路口，因为每段路程的车辆承载量和目前平均通过量各有不同，因此，本文通过建立规划建模求解，得出货物运输效率最大的研究方法就显得非常有意义[3]。当前，在某市东部区域有一公司的配送中心，将派出运输车把货物送到本市西部区域仓库储存，其交通线路图如图1所示。

根据该市交通运输部门统计，配送中心到仓库各交通路口的最大允许车流量和日平均车流量如表1所示，括号里第一个数字代表该公路最大允许的车流量（路段容量），第二个数字表示当下的车流量。

2    问题分析

根据上述实际问题分析，不妨将该问题转化为数学问题处理。该运输问题的处理和解决属于优化模型中的线性规划模型，目标显然是运输网络流入量或流出量最大。在运输过程中，不妨把这7个地理位置看成是7个网络流节点，配送中心看成是起点，仓库看成是运输的终点。同时，满足4个约束条件。一是每个路段通行的最大流量不大于路段容量，那么12条路段就可以得到12个约束条件。二是满足流量守恒约束条件，每个路口流入的车流量等于该路口流出的车流量。即路口1流入的车流量等于该路口流出的车流量，路口2流入的车流量等于该路口流出的车流量，路口3流入的车流量等于该路口流出的车流量，路口4流入的车流量等于该路口流出的车流量，路口5流入的车流量等于该路口流出的车流量。三是整个网络流入量的和与流出量的和相等。四是每个路段上的流量一定是非负的[4]。然后利用Lingo软件解除最优解，得到运输问题的处理和解决最优方案。

3    模型的建立与求解

3.1    模型建立准备

将配送中心、仓库、路口1、路口2、路口3、路口4、路口5用数学符号表示，如表2所示。

不妨将配送中心到仓库交通线路和配送中心到仓库各交通路口的最大允许的车流量及日平均车流量用运输网络图表示，如图2所示。其中，括号里第一个数字代表该公路最大允许的车流量（路段容量），第二个数字表示当下的车流量，箭头表示车辆运行的方向。

3.2    模型建立

为使网络流入量和或流出量和最大，综合考虑路段最大流量约束、每段路流量守恒约束以及整个网络流量约束，建立如下规划模型。

3.2.1    目标函数的确定

设fij（i=1，2，3，4，5，6，7；j=1，2，3，4，5，6，7）表示各路段边的最大流量为决策变量。建立线性规划模型，选择流入量和的最大化为问题目标，则目标函数为：

max z=f12+f13。

式中：max z表示网络流入量和或流出量和最大，f12表示配送中心到路口1的最大流量，f13表示配送中心到路口2的最大流量。

3.2.2    每个路段要求的最大流量不大于路段容量，12个路段有12个约束条件

f12≤13      f36≤5

f13≤9        f45≤13

f24≤6        f46≤4

f25≤5        f47≤4

f32≤4        f57≤9

f34≤5        f67≤10

3.2.3    每段路流量守恒约束

f12+f23=f24+f25

f13=f32+f34+f36

f24+f34=f45+f46+f47

f25+f45=f57

f36+f46=f67

3.2.4    整个网络流入量的和要与流出量的和相等，也是遵循流量守恒定律

f57+f47+f67=f12+f13

3.2.5    每个路段上的流量非负约束

fij≥0，i=1，2，3，4，5，6，7；j=1，2，3，4，5，6，7

综上所述，运输网络最大流的模型如下。

max z=f12+f13

f12+f13=f24+f25

f13=f32+f34+f36

f24+f34=f45+f46+f47

f25+f45=f57

f36+f46=f67

f57+f47+f67=f12+f13

f12≤13      f36≤5

f13≤9        f45≤13

f24≤6        f46≤4

f25≤5        f47≤4

f32≤4        f57≤9

f34≤5        f67≤10

3.3    模型的求解

對于上述规划模型，可以使用Lingo软件编程求解。解得z=20，即网络最大流为20，也就是说如果该区域流入量大于20，网络可能发生拥堵，只要小于20，就能保证不堵车。另外，解得f12=11，f13=9，f24=6，f25=5，f34=4，f36=5，f45=2，f46=4，f47=4，f57=7，f67=9。即配送中心到路口1的最大流量为11，路口1到路口2的最大流量为9，路口1到路口3的最大流量为6，路口1到路口4的最大流量为5，路口2到路口3的最大流量为4，路口2到路口5的最大流量为5，路口3到路口4的最大流量为2，路口3到路口5的最大流量为4，路口3到路口6的最大流量为4，路口4到路口6的最大流量为7，路口5到仓库的最大流量为9。由于整体网络中的流量守恒和相互约束等因素，各路段求出的流量尽管都小于或者等于路段容量，但是已经是该路段的最大流量[5]。

4    结果分析与推广

本文建立的模型与实际紧密联合，结合实际建立规划建模求解，其模型的结果与实际相符，这使模型贴近实际，通用性、推广性较强；模型原理简单明了，容易理解与运用；模型的建立根据实际问题要求，得到的模型可信度较高[6]。当然，该线性规划模型还可以有其他很多解法，比如可以用EXCEL来解，先构建模型框架，将目标函数和约束条件依次放入EXCEL中，然后运用规划求解工具求解，选择求解方法为“单纯线性规划”，即可求解到结果。比较几种方法，建立规划模型不失为一种较为理想的解决问题的方法。

参考文献：

[1] 张丰，罗罕勋．一类网络最大流问题的简便算法[J]．中国科技信息，2009（7）：265-266.

[2] 郭鑫龙．几类求解最大流问题算法在运输问题中的应用[J]．电子制作，2015（18）：50.

[3] 谢凡荣．求解网络最大流问题的一个算法[J]．运筹与管理，2004（4）：37-40.

[4] 张超，胡振威．有流量需求和分品种容量限制的运输网络最大流算法[J]．交通运输工程与信息学报，2017，15（3）：121-127.

[5] 韩中庚．数学建模实用教程[M]．北京：高等教育出版社，2012．

[6] 孙君，钟茂林，杨叶勇，等．供应链数据分析[M]．北京：清华大学出版社，2021.