基于三元深度融合的行为驱动成绩预警模型

庄俊玺，王 琪，赖英旭，刘 静，靳晓宁

北京工业大学信息学部，北京 100124

教育是国之大计，高等教育作为教育的重要组成部分，其发展状况从侧面反映了国家科学技术的发展水平。高等教育的普及化给高校教学管理工作带来了新的挑战，如何在高等教育受众增加的同时实现内涵式发展是我国高等教育发展面临的重大课题。在这种情况下，期末成绩作为衡量高等教育教学质量的直观标准，如何精准地预测其变化已成为迫切需求。

成绩预测预警的主要目的是发现存在学业危机和具有潜力的学生，以便教师及时采取干预措施帮助其提升学业。现有的成绩预测方法大多采用数据挖掘的技术，如分类、聚类、回归、关联规则[1]。Gao 等[2]基于学生编程过程中的行为模式，使用差分序列挖掘的方法来预测学生最终的课程表现。Song 等[3]针对学生的在线点击日志、历史成绩和人口统计信息设计了一种基于顺序参与检测机制的模型来捕获学生的顺序参与特征同时探索周期性特征进而预测学生的学习成绩。Haryani等[4]使用分类和聚类技术处理学生满意度调查和校园设施调查得到的反馈数据，以帮助大学分配资源、制定政策进而提高教育质量。郭鹏等[5]使用改进的K-means算法和引入兴趣度量的Apriori算法对学生的成绩记录进行挖掘以发现课程之间的关联规则和相互影响。张明焱等[6]结合长短期记忆网络（long short-term memory，LSTM）自动编码特征和注意力机制提出一种风险学生早期预警模型，它可以有效地识别出风险学生并得到最早干预时间点。

除了以上针对人口统计特征、心理因素、在线学习数据等信息的成绩预测研究，基于学生一卡通消费数据、门禁数据这类在校行为数据的研究也有很多。Liang等[7]基于极限梯度提升算法（extreme gradient boosting，XGBoost）和改进的粒子群优化算法（particle swarm optimization，PSO）相结合的模型来解决学生成绩的多分类问题进而预测学生的学习成绩，不过该方法缺少对日常行为数据的关注；Yao 等[8]基于校园智能卡在信息中心生成的数字记录构建校园社交网络，并使用一种新的标签传播算法来预测学生的表现，但该方法基于学生消费、进出图书馆等行为来构建社交网络，缺少对日常行为本身的关注；Xu 等[9]根据学生的出勤率、在图书馆的平均时间、玩游戏的平均时间和参加的社团数量等信息使用K近邻（K-nearset neighbors，KNN）算法来预测学生是否能顺利完成学业，实验过程中使用的数据特征单一；Chen 等[10]针对人口统计特征、历史表现数据和一卡通数据提出一种基于多头注意力机制和分层渐进LSTM行为特征提取模型来预测学生的成绩变化，预测过程中对行为数据的利用不充分；Chen等[11]根据学生的消费记录、考勤结果、课程成绩、图书借阅等行为信息使用组合梯度提升树算法（gradient boosting decision tree，GBDT）、人工神经网络（artificial neural network，ANN）和K-means 算法的预测模型来预测学生的学习成绩和生活规律，在提取学生日常行为数据时粒度较粗。

针对以上研究存在的对日常行为数据关注较少、对行为数据的利用不充分、使用的数据特征单一、数据粒度粗等问题，本文提出一种基于三元深度融合的行为驱动成绩预警方法，该方法重点关注学生的细粒度日常行为数据，并从规律性、活跃性、勤奋性三方面入手来提取行为数据，然后使用支持向量机递归特征消除算法（support vector machines recursive feature elimination，SVM-RFE）做特征选择操作，最后搭建了一个三元深度融合成绩预警模型来完成对学生的分类进而进行成绩预警。实验结果表明，本方法提出的模型有较好的分类预测效果，可以有效地帮助高校教师和辅导员进行教学干预。

1 相关工作

1.1 群体行为

社会学家对群体行为的研究由来已久。LeBon[12]认为群体行为是由成员自发形成的，它会随着时间的推移强化或消失，主要受群体环境的影响，群体中的个人容易模仿群体中其他人的行为和态度。Park 等[13]认为，“群体行为是在公共和集体冲动的影响下发生的个人行为，它是社会互动的结果”。波普诺[14]认为，群体行为是那些在相对自发的、无组织和不稳定的情况下人们因为某种普遍的影响和鼓舞相互作用而发生的行为。由此可见群体行为是自发形成的，它是群体中各参与者相互影响的结果。国内关于群体行为的研究经常与政治和群体性事件相联系，本文则从高校不同学生群体间的行为模式入手来研究群体行为。高校学生在日常生活中多以群体形式存在，班级同学经常一起上课，朋友经常一起吃饭运动，社团成员经常一起举办活动，这使得他们往往具有群体共同目标和价值追求，因此他们在校期间的成绩很容易受到所处群体的影响。Yang 等[15]发现学生间存在较强的同伴效应，作息规律的学生倾向于交校园行为有规律的朋友，一个勤奋的学生，他的朋友也很勤奋。Tsai等[16]发现学生在以小组为单位搜寻信息完成任务时尤其会考虑组内成员的想法和意见，他们往往会放弃同伴不需要的信息。Cheng等[17]发现学生在线学习过程中组内互动可以更好地发展他们的创造力、批判性思维和解决问题的能力。Liu[18]发现给学生推荐学习资料时，考虑群体学习行为比不考虑群体学习行为的推荐结果有更高的准确率，学生的满意度也更高。

由此可见，高校学生群体间的行为具有较高的相似性，在进行研究时考虑群体行为的情况下效果更好，所以本文基于群体成员相似的行为模式和学生行为的规律性、过程性、周期性等特点从群体行为的角度出发来选择特征。另外，群体行为不是群体的产物，而是由将特定行为带入群体的一些人集合形成的，是相似个体行为集合的产物，因此，本文不仅分析了学生的群体行为，还考虑了学生个体的表现。

1.2 特征选择

特征选择可以从原始特征中剔除不相关的或冗余的特征以优化数据集，它不仅能加速模型训练的过程，还能在一定程度上提高模型分类的精度。根据算法与模型的结合方式可以将特征选择算法分为三类，分别是过滤式特征选择算法、包装式特征选择算法、嵌入式特征选择算法。考虑到过滤式特征选择方法因选择特征过程与模型独立所以选出的特征在模型中表现不如包装式特征选择算法，而包装式特征选择算法计算量大，影响系统效率，本文选用嵌入式特征选择算法完成这一操作。常用的嵌入式特征选择算法有SVM-RFE 算法、最小绝对值选择与收缩算子（least absolute selection and shrinkage operator，Lasso）回归和岭（ridge regression，Ridge）回归。考虑到Ridge回归不能使特征的权重系数为0 所以不适用于减少特征数量的场景，Lasso 回归在特征相关性较强时结果不稳定，而SVM-RFE 算法既能递归地减少特征数量又不会受特征间相关性影响，本文使用SVM-RFE算法来选择特征。

SVM-RFE算法是支持向量机（support vector machine，SVM）算法与递归特征消除（recursive feature elimination，RFE）相结合组成的。其中，SVM是一种应用于分类、回归问题的有监督学习算法，它使用一条到最近点边界、有宽度的线条来区分各种类型，选择边界最大的那条线是模型最优解，边界上的点是拟合的关键点，被称为支持向量。递归特征消除是一个基于贪婪算法的特征选择框架，可以嵌入到不同的分类器中使用。SVM-RFE算法是RFE 框架嵌入到SVM 分类器中的应用，它在特征选择的过程中以SVM的权重向量系数作为特征排序准则，每一步都迭代移除权重系数最低的特征，再用剩余的特征继续训练，直到选出所需数量的特征子集。

2 模型描述与实现

2.1 问题定义与特征工程

给定单个学生的特征集合M,M由学生的群体行为特征和个体行为特征组成，即M={m1,m2,m3},mi={xr1,xr2,…,xrn},其中m1是学生群体消费行为、进出图书馆行为、进出宿舍行为中的规律型行为数据，m2、m3分别是学生个体消费行为中的活跃型行为数据和个体进出图书馆行为中的勤奋型行为数据，xri表示某一时间各特征的值，n是周期总数。对于该学生，他的成绩加权排名为s，根据排名可将学生划分等级y，本文的目的是使用给定的学生特征集合M来预测学生的等级y以完成对学生分类进而进行成绩预警。

受大五人格模型启发，本文重点关注五大人格中的责任程度，提取群体行为中的规律性特征。原始的消费数据包含学号、消费类型、消费地点、消费时间、消费金额等字段，在提取规律型行为时，本文从消费类型、消费地点、消费时间这三个字段入手进行分析。

对消费类型的记录总数和消费地点情况统计可以发现，有消费地点的消费类型有五种，这五种消费类型的记录总数如表1所示，考虑到除“POS消费”外其他类型的记录数较少，实验过程仅使用“POS 消费”的数据。在此基础上对各消费地点的记录总数统计可得到表2的结果，所以在提取规律型行为时，消费数据中仅考虑记录总数最多的五个地点。

表1 各消费类别的记录总数Table 1 Total number of records for each consumption category

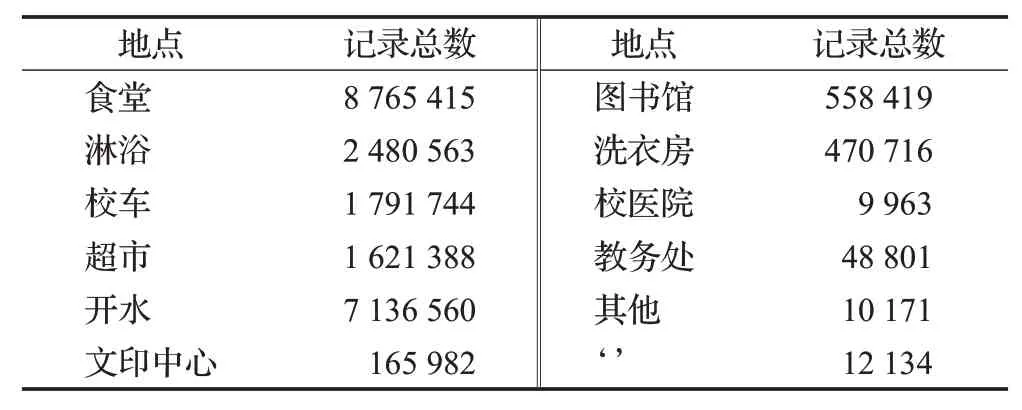
表2 各消费地点的记录总数Table 2 Total number of records for each consumption location

然后对学生在这五个地点的消费时间进行分析，实验过程中以一个小时为单位进行时间切片，可以得到图1所示的结果。

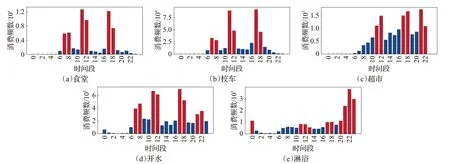
图1 五个地点各个时间段的消费频数Fig.1 Consumption frequency of each time period in five locations

校园生活中学生正常作息情况下的消费时段大致相同，由图1可看出学生各个地点的消费时间呈明显的聚集状态，红色的时间段即消费频数高的时间段，本文根据学生在消费频数较多的时段是否有刷卡行为来提取学生行为的规律性。为了更好地记录学生的早出晚归情况，在提取超市这一地点的规律型行为时，添加了6：00 至9：00 这一时间段来记录学生的早出情况，在提取校车这一地点的规律型行为时，添加了20：00至24：00这一时间段来记录学生的晚归情况，提取食堂的规律型行为时同样考虑了吃早饭较早和吃晚饭较晚这两个时间段，最终得到各地点的时段数如表3所示。

表3 各个地点的时段总数Table 3 Total number of time slots for each location

学生早上抵达图书馆的时间、晚上离开图书馆的时间以及早上离开宿舍的时间往往能反映学生学习的勤奋程度，因此在提取规律型行为时考虑了到图书馆较早、离开图书馆较晚、离开宿舍较早这三类学生群体。对图书馆门禁数据和宿舍门禁数据中学生在各个时间段的刷卡频数统计可以得到图2所示的结果。

图2 门禁数据的时段分布情况Fig.2 Time period distribution of access control data

由图2（a）可以看出，学生早上进出图书馆行为在8：00 至9：00 这个时间段达到极大值，晚上进出图书馆行为在21：00 至22：00 这个时间段达到极大值，所以本文将上午九点之前到达图书馆的学生划为到图书馆较早的学生群体，晚上九点之后离开图书馆的学生划为离开图书馆较晚的学生群体。由图2（b）可以看出，学生上午离开宿舍的时间在8：00至9：00这个时间段达到极大值，所以本文将上午九点之前离开宿舍的学生划为离开宿舍较早的学生群体。这样就得到了学生规律型行为的24个特征。根据学生所有时间在各个地点各个时间段的刷卡情况可以生成学生的规律型行为数据Fij(1 ≤i≤n,1 ≤j≤24)，其中n为周期总数，j是当前特征对应的下标，在周期为天的情况下，若学生有刷卡行为则对应位置置1，否则为0。在周期为周或月的情况下，对应位置的值为当前周期内的频数和。

个体行为特征是学生日常行为的体现，本文以一个小时为单位进行时间切片对学生的消费数据和图书馆门禁数据进行分析，旨在从消费数据中提取学生的活跃型行为，从图书馆门禁数据中提取学生的勤奋型行为。对消费时间的消费时段进行分析发现，学生在24 个时间段均有消费行为，但1：00至6：00这5 h内的数据量较少。提取活跃型行为时，为充分提取学生行为的全局特征和局部特征，实验过程中使用这24 个时间段内的所有数据，这样就得到了学生活跃型行为的24 个特征。根据学生所有时间的消费情况可以生成学生的活跃型行为数据Vij(1 ≤i≤n,1 ≤j≤24)，其中n是周期总数，j是当天对应时段的下标。

由图2（a）可以看出进出图书馆行为频数较多的时间段有16个，在0：00至7：00、23：00至24：00这8 h内的记录几乎没有，所以在提取勤奋型行为时，为充分提取学生行为的全局特征和局部特征，实验过程中使用除这8 h外的其他16个时间段内的所有数据。这样就得到了学生勤奋型行为的16 个特征。根据学生所有时间的进出图书馆情况可以生成学生的勤奋型行为数据Lij(1 ≤i≤n,1 ≤j≤16)，其中n是周期总数，j是当天对应时段的下标。

考虑到学生寒暑假期间的在校行为数据与其他时期相比较少，会造成张量稀疏、增加模型计算量等问题，在进行特征选择前先将寒暑假期间的数据筛除。以周为单位对消费数据、图书馆门禁数据进行分析可得到图3所示的结果。

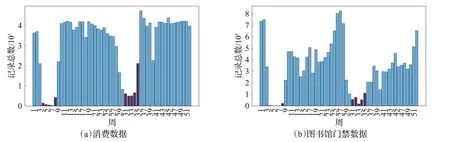
图3 学生数据的周分布情况Fig.3 Weekly distribution of student data

可以看出，学生在一年内的第4周～第8周、第30周～第34周的记录比较少，在进行后续操作前需要先将这10周的记录删除。

本文使用SVM-RFE算法执行特征选择操作，SVMRFE算法在特征选择后将给出所有特征的得分排名，排名越小意味着该特征越重要，除此之外还会给出所有特征对应的support_，support_是由true、flase组成的向量，若特征所在位置对应的值为true 则表示该特征被选中。考虑到将学生的三类行为数据按周期总数展开后分别有n×24、n×24、n×16 个特征，其中n为周期总数，在这种情况下，不同时间不同特征的重要性不一定相同。所以在进行特征选择时，使用support_为true 的所有特征中64 个特征出现的总天数来判断特征的重要性。三类行为数据特征选择的结果如图4所示，筛除出现频次较少的特征后，最终得到的三类行为数据的特征数分别为21、19、14。

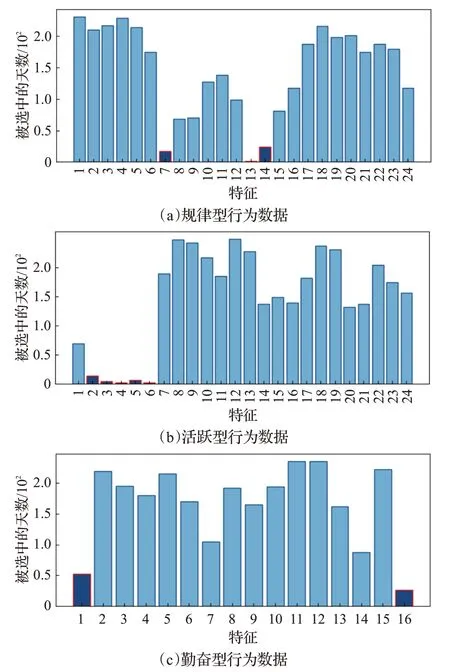
图4 特征选择的结果Fig.4 Results of feature selection

2.2 模型结构

本文基于端到端深度学习的方式建立了三元深度融合成绩预警模型（ternary deep fusion network，TDFN），该模型由四部分组成，分别是规律性特征提取模块、活跃性特征提取模块、勤奋性特征提取模块、三元深度融合成绩预警模块，其总体架构如图5所示。规律性特征提取模块使用LSTM 从规律型行为数据中提取群体行为的规律性特征，活跃性特征提取模块使用CNN 从活跃型行为数据中提取个体行为的活跃性特征，勤奋性特征提取模块使用CNN从勤奋型行为数据中提取个体行为的勤奋性特征，三元深度融合成绩预警模块将得到的规律性向量、活跃性向量和勤奋性向量拼接，然后使用全连接层基于融合后的三类行为实现一个成绩预警模型来对学生分类进而进行成绩预警。

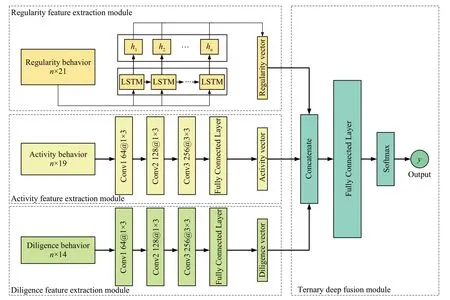
图5 TDFN架构图Fig.5 Architecture of TDFN

2.2.1 基于群体行为的特征提取

首先要提取群体行为特征，学生在校的群体行为因课程和时间影响呈现天然的规律性、过程性、周期性，考虑到群体行为的时序特征和LSTM具有长时记忆、能学习长期依赖关系等特点，本文使用LSTM来构建规律性特征提取模块，该模块包含三层：输入层、LSTM 层、输出层。输入层为学生的规律型行为数据，记为：

其中，n是周期数，表示第i位学生第t天的规律型行为数据，由18个与消费行为相关的特征和3个与进出行为相关的特征组成。

LSTM 层由多个LSTM 单元组成，LSTM 单元的结构如图6所示，它通过输入门、遗忘门、输出门的控制完成特征的存储与更新。用i、f、o、σ、W、b分别表示输入门、遗忘门、输出门、sigmoid函数、权重矩阵、偏置向量，t时刻各个门的处理过程如下：

图6 LSTM单元结构Fig.6 Unit structure of LSTM

遗忘门决定学生在t-1 时刻哪些历史行为特征被遗忘以避免梯度消失和梯度爆炸问题。例如，对学生而言，开学前几天的行为对成绩的影响程度不如期末考试前的行为，学期开始时的部分行为特征就会被遗忘。其计算方式如下：

输入门控制学生当前时刻多少行为特征被保留，即当前时刻的规律型行为中有多少会被保存在细胞状态。例如，学生在期末考试前经常很早到图书馆间接说明了该学生学习较勤奋，他在这段时间到图书馆较早的行为特征就会被保留。其计算方式如下：

在得到新的细胞状态向量值C͂t后可以更新细胞状态，更新过程如下：

输出门控制当前时刻的细胞状态Ct中哪些内容将会被输出，其计算方式如下：

输出层由隐藏层状态组成，它也是学生的规律性向量rv。

2.2.2 基于个体行为的特征提取

CNN 最早应用在计算机视觉领域，近年来其他领域也有它的影子。它一般由卷积层、池化层、全连接层组成，其中卷积层使用不同的卷积核来提取特征，池化层对卷积层提取到的特征筛选，使用最大池化或平均池化来压缩特征实现降维，全连接层连接所有特征并输出。为了充分提取学生个体行为的全局特征和局部特征，本文借助CNN 构建了活跃性特征提取模块和勤奋性特征提取模块来分别提取消费行为中的活跃性特征和进出图书馆行为中的勤奋性特征。以活跃性特征提取模块为例，该模块包含三层：输入层、CNN层、全连接层。输入层为学生的活跃型行为数据，记为X∈Rt×d。

其中，d是周期数，t是时段数，消费数据中t为19。xij表示学生第i天的第j个时间段是否有消费行为，若学生有消费行为，xij为1，反之为0。

CNN层的详细结构如图7所示，它使用多个卷积核h∈Re×k来捕获个体活跃型行为的局部特征，把学生每天在e(e≤t)时间段的刷卡信息连接起来，就形成了一个二维张量记为Vn:n+k-1∈Rt×d，卷积操作的计算方法如下：

图7 卷积层的详细结构Fig.7 Detailed structure of convolutional layers

其中，f为激活函数，h是e×k的卷积核，e(e≤t)、k(k≤d)表示窗口大小，*是卷积操作。为了使模型不依赖于初始化权重同时加快模型收敛速度、防止模型过拟合，在卷积后引入了Batchnorm层来归一化提取到的特征从而在一定程度上突出特征向量间的差异。学生的活跃型行为数据X经过卷积层处理生成了活跃性特征向量fav。

全连接层以学生卷积后得到的活跃性特征向量fav为输入，为避免训练过拟合加入了Dropout 层使节点间的连接随机失活，为提高模型的非线性表达能力加入了ReLU激活函数层，fav经过全连接层生成学生的活跃性向量av，即av=MLP(fav)。

勤奋性特征提取模块和活跃性特征提取模块的特征提取方式相似，它的输入为勤奋型行为数据，输入层中的t为14。值得注意的是，因为两个模块输入数据的尺寸不一致，所以在实验过程中，它们卷积层步长的值并不一致，全连接层参数的大小也不一样。卷积层处理后生成了勤奋性特征向量fdv，全连接层以fdv为输入最终得到了学生的勤奋性向量dv，即dv=MLP(fdv)。

2.2.3 基于三元深度融合的成绩预警

三元深度融合成绩预警模块将规律性特征提取模块、活跃性特征提取模块、勤奋性特征提取模块输出的规律性向量rv、活跃性向量av、勤奋性向量dv以拼接的方式进行融合得到完整的特征向量radv，该过程可形式化表示为：

然后将融合后得到的特征向量radv送入全连接层来预测学生的成绩。本文使用两层全连接网络来完成分类预测任务，隐藏层间加入了ReLU 激活函数层和Dropout层以达到更好的训练效果，然后馈入Softmax层估算学生属于各类别的概率越高表明学生属于当前类别的可能性越大，对于不同类别的学生，老师应给予的帮助不同。该过程可形式化表示为：

模型训练过程中使用交叉熵损失函数，该函数通过最小化损失值来学习所有参数：

其中，N为训练集中学生总数，y(i)是学生i的真实排名等级，若学生排名在学院的前80%则y(i)取0，否则取1。

3 实验与结果分析

3.1 实验数据

3.1.1 数据集

本文使用DataCastle 竞赛中的公开数据集，数据集是学生2013—2014、2014—2015 这两个学年的原始在校行为数据，考虑到两个学年学生行为间存在差异且第二学年学生人数比第一学年多，本文使用第二学年的学生数据展开研究。将第二学年的学生按成绩加权排名分为两类，其中成绩排名在后20%的为正样本，成绩排名在前80%的为负样本，然后将数据集按6∶2∶2的比例划分为训练集、验证集、测试集，它们的样本数如表4所示。

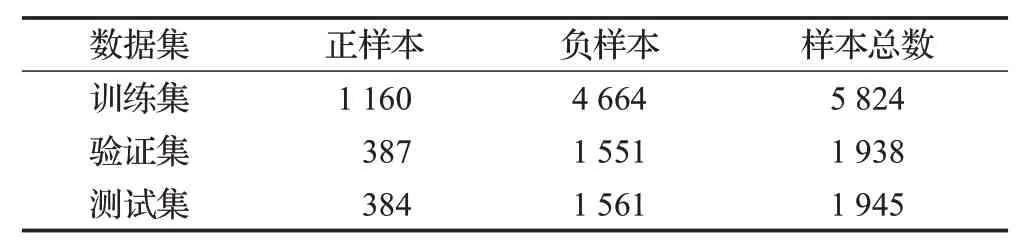
表4 数据集统计结果Table 4 Dataset statistics results

3.1.2 评价指标

考虑到数据集中正负样本不均衡，实验采用Accuracy（准确率）、Weighted_Precision（加权精确率）、Weighted_Recall（加权召回率）、Weighted_F1（加权F1 指数）四个指标对预测结果进行评估，它们的计算过程如下：

其中，TP、TN 分别为分类正确的正样本个数、负样本个数，FP 为真实标签为负但预测标签为正的样本数，FN 为真实标签为正但预测标签为负的样本数。TPi、TNi、FPi、FNi是将第i类标签看作正样本时得到的各类样本数，Precisioni、Recalli、F1-scorei是将第i类标签看作正样本时得到的精确率、召回率、F1指数，wi表示真实标签中第i类标签的占比。考虑到样本不均衡时使用Accuracy评估模型分类能力时效果不佳，实验过程中重点关注后三个评价指标的表现。

3.1.3 实验参数设置

本实验使用PyTorch 框架来搭建模型，并在显存为8 GB、型号为GeForce RTX 3070 的GPU 上加速训练。在实验中，对除寒暑假外的295天数据编码生成三类行为数据，实验参数的设置情况如表5所示。

表5 实验参数的设置情况Table 5 Setting of experimental parameters

3.2 对比模型

为了验证本文提出的三元深度融合成绩预警模型的预测性能优于其他深度学习模型，本文分别选取SPDN模型[19]、GritNet模型[20]和TBCNN[21]模型进行对比实验。

（1）SPDN 模型：该模型将学生的行为序列分为13周，将网页浏览行为、在线学习行为及行为之间的时间差分别编码后输入嵌入层模型转化为稠密变量，然后使用多源融合CNN 模块提取周特征表示向量，接着融合周特征表示向量和静态特征中的分组、聚类模式后送入BiLSTM 层并将输出依次馈入全连接层、Softmax 层以估算学生存在学业风险的概率。本文在对比实验时选择当前数据集，使用42周学生的行为序列，以消费行为替代网页浏览行为，以进出图书馆行为替代在线学习行为，以学院替代静态特征中的分组，去掉静态特征中的聚类模式，同时将消费行为、进出图书馆行为、时间差的嵌入维数设为50，学院的嵌入维数设为18。

（2）GritNet 模型：该模型以周为单位，将学生观看讲座视频、测验回答正确等在线学习行为和对应的时间差分别编码然后输入嵌入层转化为稠密向量接着送入BiLSTM层，在输出前添加注意力层以关注嵌入序列中最相关的部分，最后将注意力层的输出顺序馈送到全连接层和Softmax层完成最终的毕业预测。本文在对比实验时选择当前数据集，使用42周学生的行为序列，融合消费行为和进出图书馆行为替代在线学习行为。

（3）TBCNN模型：该模型以学生一学年的在校行为数据为基础，采用行、列、深度三个维度的卷积和注意力操作来捕捉学生行为的持久性、规律性和时间分布，并将学生成绩预测问题视为top-k排名问题，以保证识别困难学生的准确性。该模型使用的数据集与本文使用的数据集相同，本文在对比实验时将学生成绩预测问题视为分类问题来进行。

3.3 对比实验

将本文提出的TDFN模型与SPDN模型、GritNet模型和TBCNN 模型在相同的公开数据集上进行对比实验，并使用Accuracy、Weighted_Precision、Weighted_Recall、Weighted_F1 等评价指标来评估这三个模型，实验结果如表6所示。

表6 对比实验的结果Table 6 Results of comparative experiments

可以看出，本文提出的模型在加权F1 指数方面可以达到0.854 2，它的各项指标均高于其他模型，和SPDN相比在加权精确率、加权召回率、加权F1指数方面分别提升了0.130 8、0.120 1、0.116 3，和GritNet 相比在加权精确率、加权召回率、加权F1 指数方面分别提升了0.119 1、0.132 5、0.117 2，与TBCNN相比在加权精确率、加权召回率、加权F1 指数方面提升了0.024 3、0.029 8、0.027 7。以上结果体现了本模型在成绩预警时的优越性。

考虑到TBCNN 和TDFN 预测性能相近，本节对其复杂度进一步分析，以FLOPs、参数量为评价指标，可以得到表7所示的结果。

表7 模型的复杂度分析Table 7 Complexity analysis of model

可以看出，本文提出的TDFN模型训练过程中的计算量FLOPs远小于TBCNN模型，能有效地提高模型的效率，但TDFN 模型要训练的参数总数Params 远大于TBCNN模型。

3.4 不同参数值对结果的影响分析

为了观察不同参数值、不同优化算法对模型预测性能的影响，本节将对比分析参数中不同的Batchsize、不同的学习率、LSTM结构中不同的隐藏层维度以及不同优化函数对模型预测精度的影响。其中，不同Batchsize值、不同学习率、LSTM 结构中不同隐藏层数量的实验结果分别如表8～表10所示。

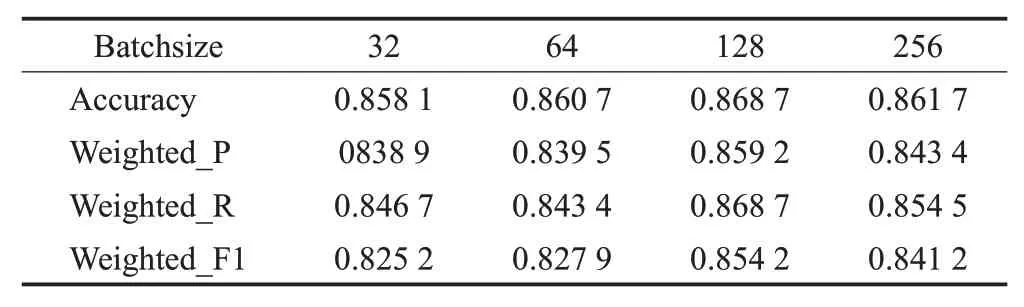
表8 Batchsize对结果的影响分析Table 8 Analysis of impact of batchsize on results

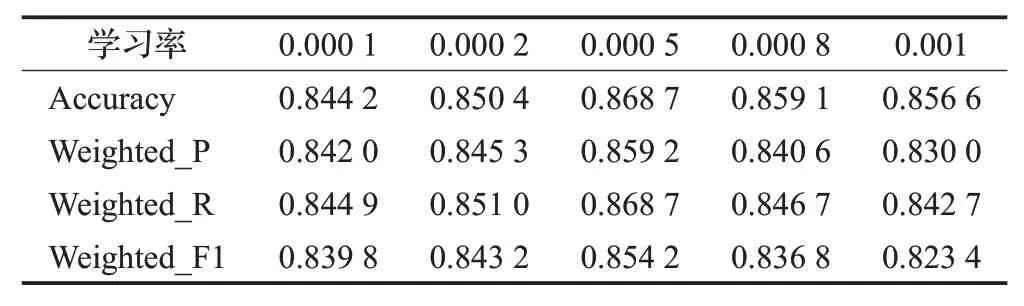
表9 学习率对结果的影响分析Table 9 Analysis of influence of learning rate on results

表10 Hidden_size对结果的影响分析Table 10 Analysis of influence of Hidden_size on result

可以看出，随着Batchsize的增大，学习率的增大，隐藏层数量的增多，模型预测时的加权F1 指数均存在先升后降的趋势，当Batchsize为128、学习率为0.000 5、隐藏层数量为128时模型预测性能最佳。

不同优化函数的结果如表11所示。

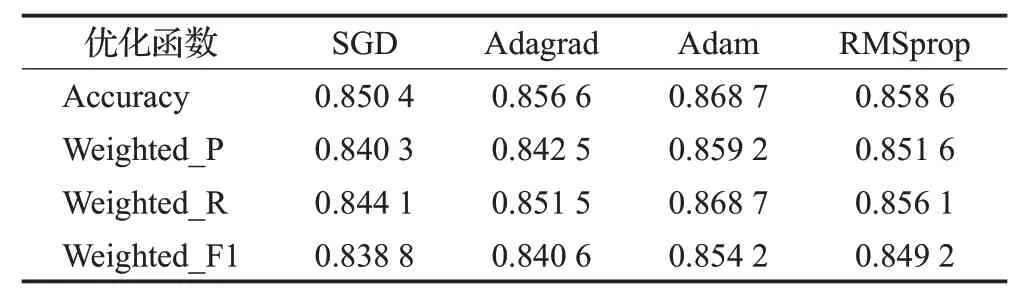
表11 优化函数对结果的影响分析Table 11 Analysis of influence of optimization function on result

可以看出，优化函数对模型预测精度也有影响，使用Adam优化算法时模型预测性能最佳。

3.5 三元特征提取模块的重要性分析

为了验证本文提出的将三类特征分别输入到三个不同特征提取模块的有效性，将TDFN模型与只有规律性特征提取模块的TDFN_L模型、只有活跃性特征提取模块的TDFN_C 模型和融合规律性特征提取模块和活跃性特征提取模块的TDFN_LC模型对比来观察本方法的有效性，其中TDFN_L 模型和TDFN_C 的输入为F、V、L三类行为数据的拼接，即concatenate(F;V;L)，然后将结果分别送入各模块来预测学生成绩；TDFN_LC的输入分别为F、concatenate(V;L)，即规律型行为数据输入到规律性特征提取模块、将活跃型行为数据和勤奋型行为数据拼接后输入到活跃性特征提取模块。实验结果如表12所示。

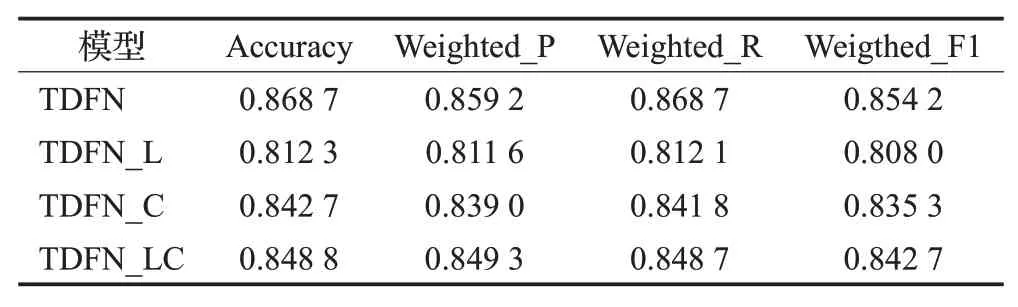
表12 模块的重要性分析Table 12 Analysis of importance of modules

通过对比表6中的各评价指标可以看出，将不同类别的行为数据输入到不同的特征提取模块时模型预测效果最好。即使是活跃型行为数据和勤奋型行为数据，对比TDFN 模型和TDFN_LC 模型的结果发现，使用两个特征提取模块进行预测的加权F1指数会比仅使用一个特征提取模块进行预测的加权F1指数高0.011 5。

以FLOPs 和参数量为评价指标对三个特征提取模型的复杂度进行分析，可以得到表13所示的结果。

表13 模块的复杂度分析Table 13 Complexity analysis of modules

可以看出，活跃性特征提取模块的计算量和参数量均大于其他两个模块，以LSTM为基础构建的规律性特征提取模块的复杂度低于以CNN为基础构建的特征提取模块，活跃性特征模块和勤奋性特征提取模块中全连接层的神经元个数对其复杂度也有影响。

3.6 三类行为的重要性分析

为了进一步确定规律型行为数据、活跃型行为数据、勤奋型行为数据中哪一类行为数据对成绩预测预警的影响更大，针对三类行为数据分别进行了消融实验。具体地，将三类行为数据分别输入到规律性特征提取模块、活跃性特征提取模块、勤奋性特征提取模块作为基准实验，分别删除一类行为数据及其对应的特征提取模块，使用Accuracy、Weighted_Precision、Weighted_Recall、Weighted_F1这四个评价指标来观察这三类行为的重要性。实验结果如表14所示。

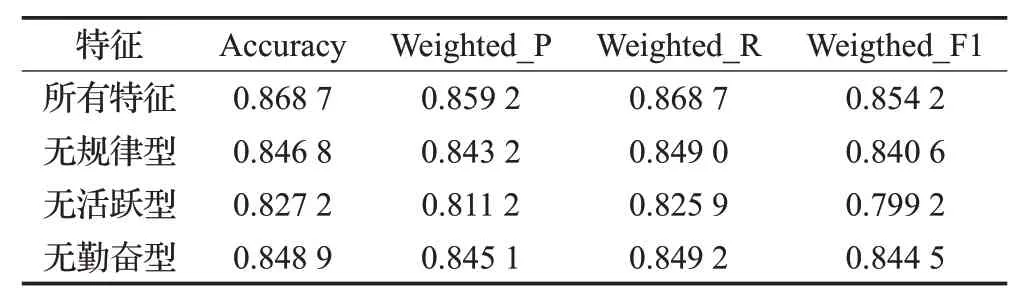
表14 三类行为数据的重要性分析Table 14 Analysis of importance of three types of behavioral data

可以看出，当数据集中没有活跃型行为数据时，模型预测时的加权F1 指数由原来的0.854 2 降低到0.799 2，下降了0.055，和不含规律型行为数据或不含勤奋型行为数据时的加权F1 指数相比也下降了0.041 4、0.045 3，这说明活跃型行为数据能更好地表现学生行为之间的差异，相较于其他两类特征，它在模型进行成绩预测预警时的作用更大。

活跃型行为数据和规律型行为数据中的绝大部分数据来自同一个原始数据且以上分析发现活跃型行为数据对模型预测性能的影响更大，这表明提取原始数据的全局信息和局部信息有利于提高模型预测精度，教育工作者可以通过敦促学生养成良好生活习惯的方式间接影响其全局信息和局部信息，从而影响学生期末时的成绩，在进一步提高模型分类预测能力时可以考虑对活跃型行为数据中的特征做进一步筛选使其更具代表性。

对三类行为数据中0、1 值占比统计可以得到表15所示的结果，可以看出，规律型行为数据、活跃型行为数据、勤奋型行为数据中的1 值占比分别是14.08%、15.85%、3.84%。

表15 三类数据的0、1值占比Table 15 Proportion of 0 and 1 values of three types of data 单位：%

和规律型行为数据中的1值占比相比，勤奋型行为数据中1 值占比低10.24 个百分点，但两者对模型预测精度的影响程度相似，这一方面表明去图书馆这类典型的学习行为对期末成绩的影响更大，教育工作者可以安排适量的自习保证学生的学习时间从而影响他们的期末成绩，另一方面证明了图书馆门禁数据在模型预测过程中的有效性，进一步提高模型预测能力时可以考虑从图书馆门禁数据中挖掘更多的信息。

总之，高校学生的学习生活习惯与最终的期末成绩密切相关，高校自由环境下不具备自我规划和自我约束能力的学生很容易出现上课期间看视频打游戏睡觉、选择课程时投机取巧避重就轻等现象，对于此类学生，教育工作者可以在因材施教的基础上对其行为进行约束，比如增加课堂互动、安排自习等。

4 结束语

本文针对当前高校在成绩预测预警方面的不足，基于高校学生的群体行为和个体行为提出了一个三元深度融合成绩预警模型，它将群体行为和个体行为分别输入到不同的特征提取模块，然后将提取到的规律性向量、活跃性向量、勤奋性向量融合，最后基于融合后的特征向量使用全连接层来完成对学生的分类以达到给不同类别学生提供不同学习建议的目的。本文在公开数据集上验证了模型的有效性，实验结果表明该模型和其他模型相比有更好的分类预测效果，也验证了三元特征提取模块的重要性，即将规律型行为数据、活跃型行为数据和勤奋型行为数据分别输入到不同的特征提取模块时模型的预测效果更好。除此之外实验也证明了活跃型行为对学生成绩影响较大，未来工作中可以对这一类行为做进一步的研究。