应用霍普金森压杆试验分析柠条动态力学特性1)

李春东 张家宁 曹丽英 张晓礼

(内蒙古科技大学,包头,014010)

柠条(CaraganakorshinskiiKom.)是豆科锦鸡儿属的通称,作为一种典型的沙生灌木,因其耐寒、耐旱、根系发达等特点,在我国土地荒漠化严重的西北地区被广泛种植。柠条除具有防风固沙能力外[1],还因其自身富含粗蛋白、粗脂肪等营养物质可用作饲用、药用或生物质燃料[2-4]。随着龄期的增长,柠条会出现枯死以及木质化现象,降低甚至丧失其价值。因此,为延长柠条的生命周期,获得较高的经济效益,需要对其进行定期平茬。但现有平茬机在平茬过程中存在茬口质量低、功率消耗大等问题,不仅严重制约了作业效率还直接降低了柠条的复茬效果[5]。为了提高茬口质量,众多学者通过准静态力学试验来研究灌木的力学特性[6-9],根据获得的力学参数进行锯切仿真以及试验,试图得到良好的切割工艺参数[10-11],但此方法不能准确的反应平茬时柠条在高应变率动态载荷的受力情况。

霍普金森压杆试验可用于测定木材的动态力学特性,获得被测材料的应力-应变曲线。刘建辉等[12]研究发现,云南松顺纹在受压时的破坏程度、抗压强度、吸能能力都随应变率的增大而增大;许威[13]使用霍普金森压杆装置对桦木的轴向、弦向、径向三个方向进行不同应变率加载试验,发现桦木的屈服强度、韧性模量、解离程度都与应变率有关;段泽明等[14]通过霍普金森压杆试验对沙柳顺纹动态力学性能测定,分析不同含水率时,沙柳的应变率效率和屈服强度。

因此,本研究以柠条为试验对象,探究柠条横纹、顺纹两个方向在动态冲击载荷作用时的力学性能,以期获得应力-应变曲线,为建立柠条的切割与损伤力学行为模型提供理论依据。

1 材料与方法

试验材料:柠条的采集按照GB/T 1927.1—2021《无疵小试样木材物理力学性质试验方法第1部分:试材采集》,选取包头市周边地区径干笔直、无病害、无明显损伤、无侧枝、5年生的柠条60株,作为试件制作原料。结合分离式霍普金森压杆试验要求以及考虑柠条自身尺寸,将试件的规格定为10 mm×10 mm×10 mm。

试验仪器与方法:试验使用分离式霍普金森压杆装置(图1),压杆的相关参数见表1。分别使用普通应变片和半导体应变片测得入射应变、透射应变,并用动态应变仪采集信号。

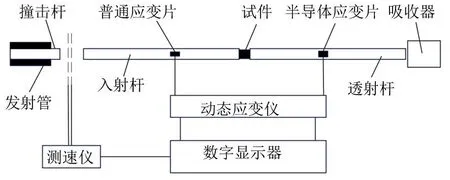
图1 霍普金森压杆试验的示意图

表1 霍普金森压杆参数

在室温条件时,按照霍普金森压杆试验方法,将两组柠条试件分别进行横纹、顺纹加载试验,通过调整发射装置驱动气压,使撞击杆产生12、19、26 m·s-1这3种不同速度撞击入射杆,以获得不同应变率时,材料的应力-应变曲线。每组试验重复3次,试验编号和试验数据见表2。

表2 霍普金森压杆试验数据

(1)

式中:t为试验加载时间(s);C0为压杆的波速(m·s-1);Le为试件的加载长度(m);E0为杆的弹性模量(MPa);A0为杆的横截面积(m2);As为试件横截面积(m2);εR(t)为反射应变;εT(t)为透射应变。

2 结果与分析

2.1 动态应力-应变曲线分析

图2(a)为柠条横纹试件在撞击杆以不同速度撞击时产生的平均应变率,分别为1 170、1 900、2 600 s-1;图2(b)为不同应变率所对应的应力-应变曲线。从图中可以看出,应变率为1 170 s-1时的应力最小,所产生的应变也最小;在2 600 s-1时的应力最大,应变也最大。图3(a)为柠条顺纹试件在撞击杆以不同速度撞击时产生的平均应变率,分别为870、1 750、2 300 s-1;图3(b)为不同应变率所对应的应力-应变曲线。从图中可以看出,应变率为870 s-1时的应力最小,所产生的应变也最小;在2 300 s-1时的应力最大,应变也最大。柠条横纹、顺纹试件的应变都随着冲击能的提高而增大,但在相同冲击能作用时,却表现出不同的应变率。根据此类现象,对柠条的横纹、顺纹两个方向分别进行动态力学特性的分析,可为柠条切割与粉碎的研究提供理论基础。

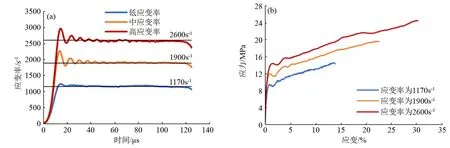
图2 柠条横纹试件应变率时程(a)与应力-应变曲线(b)

图3 柠条顺纹试件应变率时程(a)与应力-应变曲线(b)

结合数据分析可知,柠条动态压缩时,柠条的横纹、顺纹试件的动态屈服应力都与平均应变率呈正相关,因此柠条在横纹、顺纹两个方向上都对应变率敏感,具有明显的应变率效应。在柠条横纹加载试验中,应变率从1 170 s-1增加到1 900 s-1,动态屈服应力从8.96 MPa增加到11.43 MPa,增大27.57%,平均增长率为0.442;当应变率从1 900 s-1增大到2 600 s-1时,动态屈服应力随之增加到14.11 MPa,增大23.45%,平均增长率为0.637。在柠条顺纹加载试验中当应变率从870 s-1增大到1 750 s-1,动态屈服应力从57.08 MPa增加到75.50 MPa,增大32.36%,平均增长率为0.320;应变率从1 750 s-1增大到2 300 s-1时,动态屈服应力增加到105.88 MPa,增大40.24%,平均增长率为1.280。可以看出柠条顺纹方向相较于横纹方向具有更加显著的应变率效应。

柠条横纹试件的动态应力-应变曲线可分为两个阶段:第一阶段,材料受压初始阶段,发生较小的形变,内部的结构基本没有发生破坏,压力消失后可恢复到原始状态,应力-应变曲线表现为应力与应变呈正线性相关,这一阶段为弹性形变阶段;第二阶段,材料受力达到动态屈服应力后,材料内部的木质纤维先出现局部解离,又因压杆和冲击应力波的作用被迅速压实,质地相对紧密,对材料具有一定的强化作用,在应力-应变曲线上随着应变的增加所需的应力不断增大,此阶段为弱强化阶段。柠条顺纹试件的动态应力-应变曲线可分为两个阶段:第一阶段同样为弹性形变阶段;第二阶段,靠近入射杆一端的材料先达到动态屈服应力,产生裂纹并向材料内部延展,内部结构发生破坏。在应力-应变曲线上应变不断变大但所需应力却不断减少,此阶段为压溃阶段。

柠条横纹、顺纹试件的动态应变大小都随平均应变率的提高而增大。当以0.20 MPa气压对撞击杆驱动进行动态加载实验时,使撞击杆产生12 m·s-1的速度,柠条受入射杆传递的应力波发生压缩形变,横纹试件的应变量为0.138,顺纹试件的应变量为0.099;随着驱动气压增大到0.40 MPa,撞击杆获得19 m·s-1的速度,入射杆传递的应力变大,柠条的横纹试件应变量为0.225,顺纹试件的应变量为0.211;驱动气压持续增大到0.85 MPa,撞击杆获得26 m·s-1的速度,入射杆传递的应力更大,柠条的横纹试件产生的应变增大到0.303,顺纹试件产生的应变增大到0.269。综合分析,撞击杆的速度越快,材料内部产生的应力就越大,柠条试件的应变也就越大;在受到相同能量冲击时,柠条顺纹试件的应变量明显小于横纹试件的应变量,说明柠条的顺纹方向相比于横纹方向具有更高的动态抗压强度。

2.2 柠条破坏形态

随着驱动气压的提高,作用在柠条试件上的冲击力不断增大,柠条试件的破坏程度也随之改变,由于柠条横纹与顺纹试件内部纤维束的排列不同,导致两者的破环形态有所差异。从破坏形态可以看出,柠条的横纹试件和顺纹试件在霍普金森压杆试验中,平均应变率不断提高时,试件的破坏程度也不断增大。柠条横纹试件在平均应变率为1 170 s-1时,由于撞击杆的动能相对较小,试件沿纤维纹理方向产生裂纹,最后碎裂成2～3块大碎块;试件在平均应变率为1 900 s-1时,试件碎裂成多块,同时产生小尺寸碎屑,主要表现形式为木质纤维的分离;试件在平均应变率为2 600 s-1时,撞击杆的动能进一步提高,试件被进一步解离,柠条的木制纤维分离程度更大,产生大量的短而细的碎屑(图4)。结合应力-应变曲线分析,柠条横纹试件在动态加载到弱强化阶段时,存在着木质纤维束之间相互解离和摩擦,导致应力-应变曲线小幅度的波动。

图4 不同应变率时柠条横纹、顺纹试件的破坏形态

柠条顺纹试件在平均应变率为870 s-1时,试件受压缩,木质纤维发生折皱,出现轻微裂纹,但没有发生碎裂;试件在平均应变率为1 750 s-1时,随着传递的动能增加,柠条解离程度较大,试件靠近入射杆的一端率先达到动态屈服强度,试件内部产生裂纹并进一步延展,导致木质纤维发生曲折并解离,而靠近透射杆一端的解离程度相对较小;试件在平均应变率为2 300 s-1时,试件破坏严重,整体呈絮状形态,柠条受顺纹压缩时,平均应变率在达到破坏极限后,柠条的破坏形态和解离程度急剧增加。由于柠条顺纹试件在受载时,内部有裂纹的产生和延展,导致柠条的受力性大幅度降低,从而导致柠条顺纹试件的应力-应变曲线呈先升高后大幅降低的趋势。

2.3 柠条横纹本构方程模型

经过试验获得柠条的强度随着应变率的增加而增强。实现对柠条动态特性的描述将有助于对柠条研究的准确性和可预测性[15-16]。准确描述柠条在动态屈服点后的应力变化,建立与应变率相关的非线性本构模型是进行数值模拟的必要条件[17]。

在研究柠条横纹试件动态加载的应力-应变曲线时发现,展现出的动态力学特性与延展性金属相似,可通过现有对金属研究的经验模型进行分析。其中Johnson-Cook模型(J-C模型)是一个考虑应变硬化、应变速率硬化和热软化影响的动力应变模型,因所需的材料参数较少,常被用作预测材料的力学性能[18],表达式为:

(2)

σ=σi+B(ε)n。

(3)

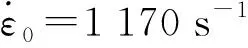
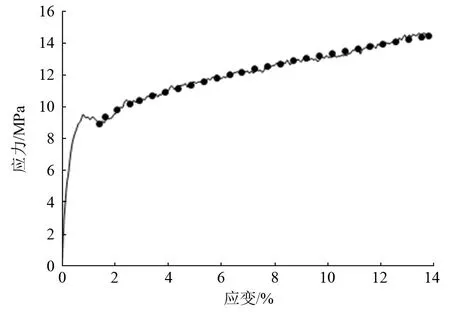
图5 柠条横纹试件(应变率为1 170 s-1)的应力-应变拟合曲线

将1 170 s-1作为参考应变率,在室温条件时,对1 900、2 600 s-1两种平均应变率的应力-应变曲线进行拟合,此时的J-C模型公式化简为公式(4),σi为1 900、2 600 s-1两种平均应变率时的屈服应力,分别为11.43、14.11 MPa,而εi则为不同应变率所对应的试件应变。R2分别为0.993 5、0.979 8,拟合效果良好。通过拟合曲线获得的应变率强化参数(C)值分别为0.213、0.088 5(图5),由此可见柠条作为应变率敏感材料,其应变率强化参数与应变率有关。

(4)

根据J-C本构模型拟合获得的曲线,与霍普金森压杆试验对柠条横纹试件加载获得的应力-应变曲线进行对比,从图6可以看出,在较低的应变率时,J-C本构模型拟合曲线与试验值基本吻合,模型预期效果良好。

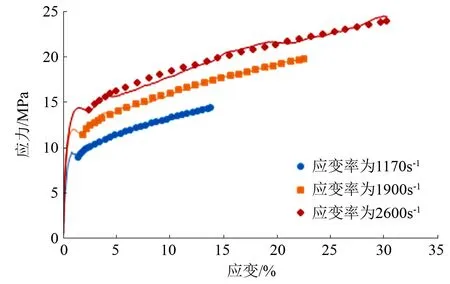
图6 柠条横纹试件的应力-应变拟合曲线

3 结论

通过霍普金森压杆试验对柠条的横纹、顺纹进行不同应变率的加载,获得的应力-应变曲线进行分析。结果表明,柠条的横纹、顺纹方向均对应变率敏感,随着应变率的提高表现出的动态应力也随之变大,具有明显的应变率效应,且柠条顺纹试件的应变率效应相较于横纹试件更加明显。对柠条两个方向的应力分析,横纹试件经历弹性形变和弱强化两个形变阶段,顺纹试件经历弹性变形和压溃两个阶段,且柠条顺纹方向相较于横纹方向能够承受更大的能量冲击,有更好的吸能能力。柠条的破坏程度与应变率有关,破坏程度随应变率提高而增大。横纹方向和顺纹方向的破坏形式也不同,柠条横纹方向破坏形式主要为木质纤维之间的解离;而顺纹方向破坏形式主要为木质纤维的折皱,整体变现为试件的压溃。在使用有限元方法研究柠条时,不可将各向同性材料替代柠条的力学特性。采用修正后的J-C本构模型,对柠条横纹试件弱强化阶段的拟合数据与试验数据拟合度良好,能够精准地描述柠条在横纹高应变率压缩时屈服强度后的力学性能。