Exploring dielectric phenomena in sulflowerlike nanostructures via Monte Carlo technique
2024-05-09SaberFadilHusseinSabbahMhirechKabouchiBahmadChaitanyJayprakashRaoraneSivaSankarSanaHassanFouadandMohamedHashem
N Saber ,Z Fadil,∗ ,Hussein Sabbah ,A Mhirech ,B Kabouchi ,L Bahmad ,Chaitany Jayprakash Raorane,Siva Sankar Sana,Hassan Fouad and Mohamed Hashem
1 Laboratory of Condensed Matter and Interdisciplinary Sciences (LaMCScI).Research Unit Labelled CNRST,URL-CNRST-17.Faculty of Sciences.PO Box 1014,Mohammed V University in Rabat,Morocco
2 College of Engineering and Technology,American University of the Middle East,Egaila 54200,Kuwait
3 School of Chemical Engineering,Yeungnam University,Gyeongsan,38541,Republic of Korea
4 Applied Medical Science Department,Community College,King Saud University,PO Box 11433,Riyadh Saudi Arabia
5 Department of Dental Health,College of Applied Medical Sciences,King Saud University,PO Box 12372,Riyadh,Saudi Arabia
Abstract This research focuses on the electric behavior of a mixed ferrielectric sulflower-like nanostructure.The structure includes a core with spin -1atoms and a shell with spin -5/ 2atoms.The Blume–Capel model and the Monte Carlo technique (MCt) with the Metropolis algorithm are employed.Diagrams are established for absolute zero,investigating stable spin configurations correlated with various physical parameters.The MCt method explores phase transition behavior and electric hysteresis cycles under different physical parameters.
Keywords: sulflower-like nanostructure,dielectric characteristics,Monte Carlo technique,phase transition,phase diagrams,electric hysteresis
1.Introduction
Efflorescence in science and nanotechnology have allowed for the successful synthesis of nanomaterials with diverse sizes and structures as well.In particular,carbon-sulfur compounds have gained colossal attention due to the possibility of using them in a myriad of organic electronic devices,including organic field-effect transistors,light modulators,light-emitting diodes,photovoltaic cells and hydrogen-storage devices [1–4].One of the recently discovered carbon-sulfur compounds that have attracted attention is sulflower [5–7].This compound has a unique molecular symmetry resulting from anti-aromaticity and orbital degeneracy,combined with its intermolecular packing due to exposed sulfur atoms,making it a promising material for organic electronics[8–10].Sulflower is chemically stable [11],making it an archetypal candidate for electronic devices.Studies have shown that thin-film OFETs made with a sulflower exhibit promising characteristics,containing a gateway threshold voltage of 45 V and a hole mobility of 9.10-3cm2Vs-1[12].Additionally,researchers have investigated the potential of sulflower systems decorated with Be2+and Mg2+to adsorb molecular hydrogen using density-functional theory (DFT)calculations [13].The decorated systems consist of cyclic polythiophene rings.In addition,DFT and time-dependent density functional theory (TD-DFT) computations have proclaimed by Shakerzadeh’s research [14] that the interaction among C16S8sulflower and a lithium atoms exhibited nonlinear optical feedback,indicating the compound’s potential as a novel nonlinear optical material.However,Donget al[15] have presented a novel method of synthesizing the first-ever fully sulfur-substituted polycyclic aromatic hydrocarbon,or‘sulflower.’This unique compound has a coronene core and represents an innovative carbon-sulfur hybrid with promising potential for various applications.
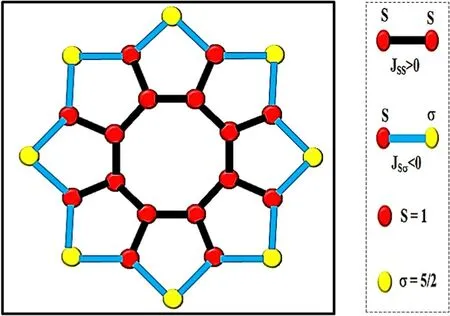
Figure 1. Schematic illustration of a sulflower-like structure,highlighting spins labeled as S (red balls) and σ (yellow balls),alongside different exchange linkages (depicted using blue and black).
In recent research,investigations of the magnetic,magnetocaloric,and dielectric characteristics of diverse structures have been done via the Monte Carlo technique (MCt),including nano-islands [16],nanowires [17],Borophene Superlattices and core–shell [18,19],graphene-like nanoribbons [20],copper fluorides [21],a nano-graphene bilayer[22],a diluted graphdiyne monolayer with defects [23],a trilayer graphene-like structure[24],a polyhedral chain[25],the Kagome Ferromagnet [26].Ising models have also been utilized to investigate the mixed systems,like the TbMnO3multiferroic system [27],the Gd2O3nanowire [28],the graphyne[29]and the core–shell Nanotube[30]systems and the Ising thin-film [31].These models have been useful in predicting magnetic phenomena in a variety of structures,from nanoscale to bulk materials.
Moreover,according to what we know,no theoretical investigations have been conducted to analyze the dielectric properties of a sulflower-like structure with a mixed spin configuration consisting of-1 and-5/2.We employ the MCt with the Metropolis algorithm to examine the dielectric characteristics of a sulflower-like structure.It is worth noting that in our previous research,we effectively utilized the MCt to inspect the magnetic and dielectric characteristics of various types of nanostructures [32–37].Furthermore,the application of an external electric field in the study of dielectric properties is crucial for understanding the response of materials to electric fields,characterizing dielectric behavior,determining polarization,dielectric susceptibility,electric hysteresis cycles,studying phase transitions,and manipulating material properties[17,18,35,36,38,39].Indeed,the study of ferroelectric or ferrielectric materials can contribute to progress in the multiferroic field [27],promising diverse applications such as magnetoelectric sensors and data storage.
This article is set out as follows: in section 2,we explain the formalism and examples of how the MCt was utilized to explore the physical properties during the simulations.In section 3,we discuss the dielectric characteristics and hysteresis demeanors,and provide our findings.First,we show the major configuration of spin in the phase diagrams in subsection 3.1.Finally,we sum up our findings in section 4.
2.Model and method
Our study focuses on studying the dielectric behavior of the sulflower-like structure inside the Blume–Capel model under free frontier circumstances.For this investigation,we utilized the MCt with the Metropolis algorithm [40–46].The nanosystem contains a total of 24 atoms,including 16 atoms with values of=±1 and 0,as well as 8 atoms with values of=±5/2,±3/2,and±1/2(figure 1).Our results involved implementing 106steps through Monte Carlo computations for every spin while neglecting the first 105steps to ensure thermal stabilization.
The Hamiltonian pertaining to the sulflower-like structure takes the form:
The terms 〈i,j〉 and 〈k,l〉 denote neighboring site pairs,specifically (iandj) and (kandl).The exchange linkages between adjacent atoms possessing spinsS-SandS—σ are represented byJSSandJSσ,respectively.The parameter μ stands for the dipole moment,and we simplify by assuming μ=1 [38,39].An external longitudinal electric field is introduced asEZ.Additionally,there are crystal fieldsDSandDσinfluencing spinsSiand σj,respectively.Our investigation is confined to cases whereDis equal toDSand toDσ.
The energy content per individual site is:
whereNT=NS+Nσ=16+8=24 defining the overall number of atoms in the studied nanosystem.
The polarizations,both partial and total,exhibited by the sulflower-like structure are as follows:
The dielectric susceptibilities,both partial and total,exhibited by the sulflower-like structure are as follows:
whereβ=,the Boltzmann’s constant,kBis utilized in this instance.To make calculations simpler,kBis set to 1.The absolute temperature is symbolized byT.
3.Results and analysis through numerical methods
The focus of this section lies in the utilization of the MCt to establish the configuration of spin in the phase diagrams in subsection 3.1.Additionally,subsection 3.2 delves into the analysis of polarizations and dielectric susceptibilities,considering their dependencies on different physical parameters.
3.1.Configuration of spin in the phase diagrams
The configuration of spin in the phase diagrams of the mixed sulflower-like structure with spins-1 and-5/2 in several physical parameters (EZ,D,JSS,and JSσ) planes are shown in this subsection.For the ground state investigation,we simulate the energy spins,we found that (2S+1)×(2σ+1)=3×6=18 possible configurations using the Hamiltonian of equation (1).These diagrams provide comprehensive information about spin configurations of the system during the adjustment of different variables.
Plotting figure 2(a) in the (EZ,D) plane for the constant values of exchange coupling interactions asJSS=1 andJσS=-0.01,it becomes evident that out of the 18 potential configurations,only 6 remained stable.Within this plane,a flawless symmetry is observable among the configurations with respect to theEZ=0 axis.Particularly,the stable configurations corresponding toEZ>0 are: (-1,+1/2);(-1,+3/2);and (-1,+5/2).Whereas the stable configurations obtained to EZ<0 are: (+1,-1/2);(+1,-3/2) and(+1,-5/2).
Figure 2(b) portrays the phase diagram within the (Jss,Ez) plane in the absence of a crystal field (D=0),while maintaining a constant exchange coupling parameter ofJsσ=-1.In this plane,only two configurations,specifically(+1,-5/2) and (-1,+5/2),remained stable,aligning with the highest spin values.
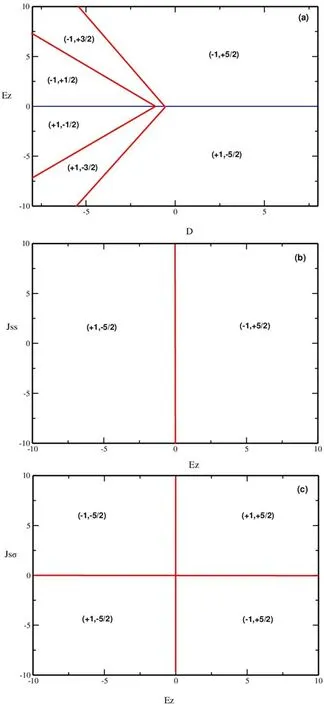
Figure 2. Configuration of spins in the phase diagrams plotted for:(a)Jss set to 1 and Jsσ to-1,followed by(b)Jsσ at-1 and D at 0,(c)Jss at 1 and D at 0,(d)Jsσ at-1 and Ez at 0,(e)Jss at 1 and Ez at 0,and finally (f) D at 0 and Ez at 0.
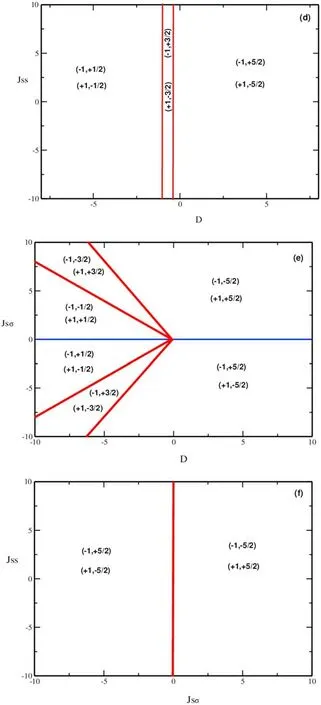
Figure 2.(Continued.)
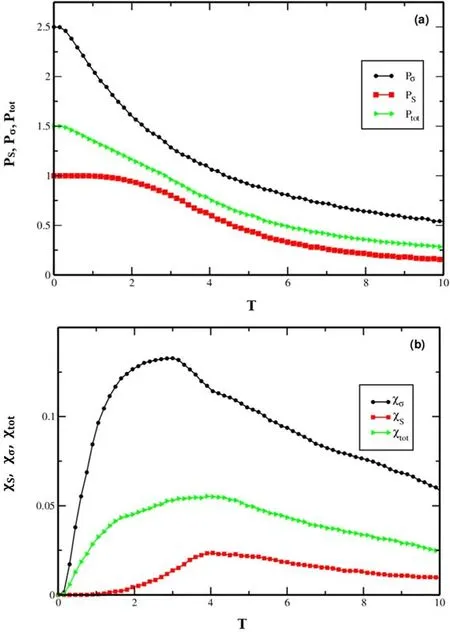
Figure 3. (a) The total of polarization,and (b) the total dielectric susceptibility relative to temperature.The depicted figures were generated using constant parameters: JSS=1,JSσ=-0.01,Ez=0.5,and D=0.
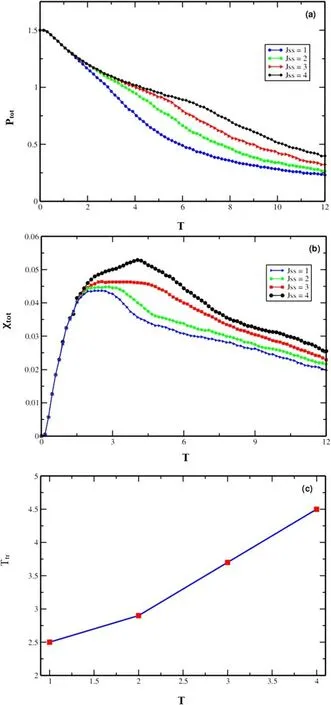
Figure 4. Total polarization (a),total dielectric susceptibility (b),in relation to temperature,and(c)transition temperature with respect to the JSS parameter.These figures were plotted while adhering to consistent parameters D=0,JSσ=-0.01 and Ez=0.5.
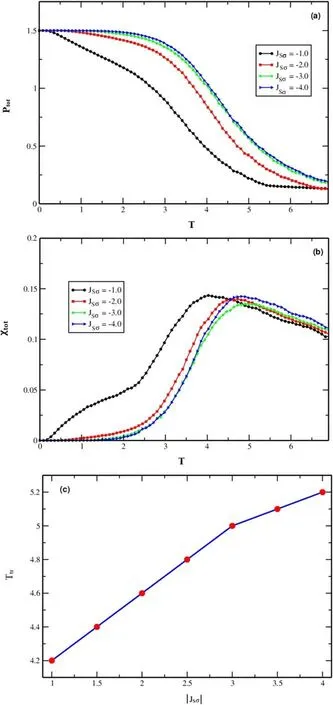
Figure 5. Total polarization (a),total dielectric susceptibility (b),in relation to temperature,and(c)transition temperature with respect to the JSσ parameter.These figures were plotted while adhering to consistent parameters D=0,JSS=1 and Ez=0.5.
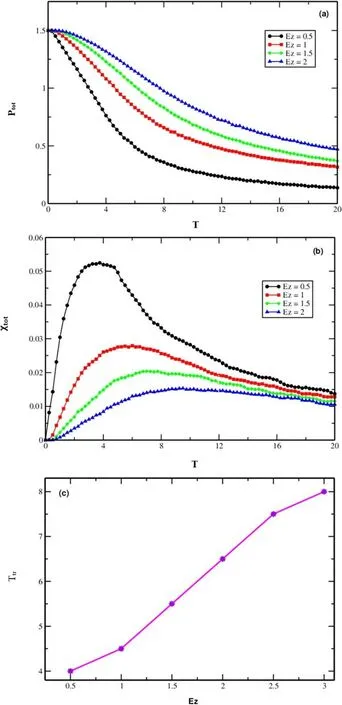
Figure 6. Total polarization (a),total dielectric susceptibility (b),in relation to temperature,and(c)transition temperature with respect to the Ez parameter.These figures were plotted while adhering to consistent parameters D=0, JSS=1 and JSσ=-0.01.

Figure 7. Hysteresis cycles of the sulflower-like structure,for different values of T for: Jss=1,JSσ=-0.01 and D=0.
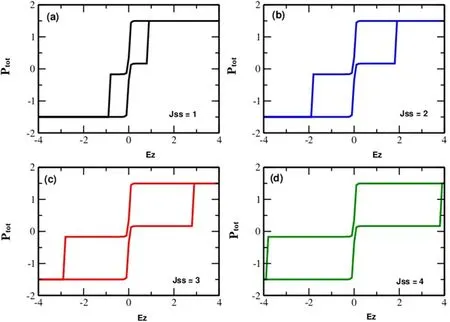
Figure 8. Hysteresis cycles of the sulflower-like structure,for different values of JSS for: JSσ=-0.01,T=0.1 and D=0.

Figure 9. Hysteresis cycles of the sulflower-like structure,for different values of JSσ when Jss=1,T=0.1 and D=0.
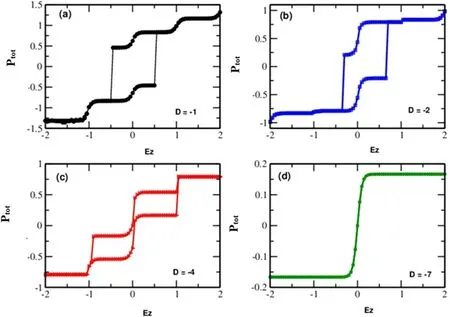
Figure 10. Hysteresis cycles of the sulflower-like structure,for different values of D for: Jss=1,JSσ=-0.01 and T=0.1.
Figure 2(c) delves into the exploration of the impacts stemming from the ferrielectric parameter (Jsσ) and the external longitudinal electric field (Ez) within the (Jsσ,Ez)plane,all while refraining from applying the external longitudinal electric field (Ez=0),and keeping the exchange coupling interaction fixed atJss=1.In this plane,stability is observed across four phases,namely(-1,-5/2),(+1,+5/2),(+1,-5/2),and (-1,+5/2).
Additionally,in figure 2(d),without applying the external longitudinal electric field(Ez=0)and with a constant value set for the ferrielectric parameterJsσ=-1,we observed that only six stable configurations exist,namely(-1,+1/2),(+1,-1/2),(+1,-3/2),(-1,+3/2),(-1,+5/2),and (+1,-5/2).The spin configurations were displayed in the (Jss,D) plane.
In order to examine how the configurations that remain stable are affected by the ferrielectric parameterJsσand the crystal fieldD,a graph was generated on the (Jsσ,D)plane withJss=1 andEz=0,as shown in figure 2(e).This graphical representation showcases six stable phases,namely:(-1,-1/2),(-1,-3/2),(-1,-5/2),(-1,+1/2),(-1,+3/2),and (-1,+5/2).
Ultimately,the impact of the ferrielectric parameterJsσand the exchange coupling parameterJsswas investigated.Figure 2(f)illustrates this exploration within the(Jss,Jsσ)plane,with fixed parametersEz=0 andD=0.In this visual representation,merely four stable configurations are evident,namely(-1,+5/2),(+1,-5/2),(-1,-5/2),and (+1,+5/2).
3.2.Monte Carlo technique (MCt)
Within this segment,the dielectric attributes of the Sulflowerlike structure are scrutinized using the MCt with the Metropolis algorithm.
The temperature-evolving tendencies of polarizations(PS,Pσ,andPtot) are presented in figure 3(a),withJss=1,Jsσ=-0.01,Ez=0.1,andD=0.At exceedingly low temperatures,partial polarizationsPS=1 andPσ=5/2 yieldPtot==1.5.The intricate relationship between spin polarization and dielectric reliability holds substantial importance,given that dielectric reliability serves as the precise indicator of the transition point where spin polarization undergoes a shift from order to disorder.This critical juncture is identified as the ‘blocking temperature,’ and it signifies a transformative phase within the system.During this phase,the system experiences a notable transition from a state of orderliness to a state of disorder,marking a significant change in its overall behavior and characteristics.As the temperature nears the transition temperature (Ttr),polarizations decrease.Interestingly,polarizations decrease as the system transitions into the superparaelectric phase around the transition temperature.For accurate determination of the transition temperature,we scrutinize the partial and total dielectric susceptibilities against temperature,employing the same parameter values featured in figures 3(a) and (b).The dielectric susceptibility peaks related to polarization transition temperatures for σ andSspins were approximatelyTtr(σ)≈2.83 andTtr(S)≈4.5,respectively.The total susceptibility also showed a peak,which occurs atTtr(tot)≈4.
Results obtained for the JSSinteraction on the total polarization and the dielectric susceptibility were summarized in figures 4(a)–(c).The results were presented for:D=0,Jss=1,JSσ=-0.01 andEz=0.5.As indicated in figure 4(a),an augmentation of theJSSparameter leads to the noticeable shifting of the transition temperature towards high temperatures.Similarly,for the purpose of identifying the precise transition temperature that distinguishes between the ferrielectric and superparaelectric phases,figure 4(b) was generated alongside the total dielectric susceptibility,with varyingJssvalues and using the same set of fixed parameter values as presented in figure 4(a).The outcome showcases that the displacement of the peaks in total dielectric susceptibility gravitates towards higher temperature values asJssvalues increase,confirming the behavior observed in the total polarization.The determined transition temperatures forJssvalues of 1,2,3,and 4 are approximatelyTtr≈2.3,2.7,3.4 and 4,respectively.Drawing upon figures 4(a) and (b),we created figure 4(c)to enhance our comprehension of how the transition temperature relates to theJSSparameter.This visual representation reaffirms the nearly linear increase in the transition temperature when increasingJSS.
To delve into the impact of the ferrielectric parameterJSσon the thermal total polarization and total dielectric susceptibility,we illustrate the behavior of this parameter in figures 5(a)—(c).These visualizations were derived across varying ferrielectric parameter values:JSσ=-1,-2,-3,and-4,all while adhering to fixed parameters:D=0,Jss=1,Ez=0.5.From the insight provided by figure 5(a),it’s evident that with an increase in the absolute value of the ferrielectric parameter |JSσ|,there is a corresponding decrease in the total polarizationPtot.Furthermore,it’s observable that the curve of the total polarization closely resembles the pattern of the total polarizationPtot(figure 4(a)).To accurately determine the transition temperature values,we mapped out the total dielectric susceptibility as illustrated in figure 5(b).The shift of the peaks of the total dielectric susceptibility towards lower temperature values becomes pronounced with an increase in the ferrielectric parameter |JSσ|.The transition temperatures identified for the ferrielectric parameters |JSσ|=1,2,3,and 4 are approximatelyTtr≈4.2,4.6,5,and 5.2,respectively.To emphasize the outcomes of figures 5(a) and(b),we delineate the trend of the transition temperature with respect to the parameterJSσin figure 5(c).This graphical representation clearly demonstrates that the transition temperature rises almost linearly as the ferrielectric parameter|JSσ|increases.
Pursuing a similar rationale,we investigated the influence of the electric field parameterEzon the thermal tendencies of total polarizations and total dielectric susceptibility across variousEzvalues (Ez=0.5,1,1.5,and 2).The outcomes are presented in figures 6(a)and(b),assumingD=0,Jss=1,andJSσ=-0.01.As depicted in figure 6(a),we observed that the total polarization diminishes towards an earlier transition temperatureTtrfor lower external longitudinal electric field values compared to higher ones.This effect arises due to the interplay between the promoting influence of the external longitudinal electric field on order within the system and the temperature’s role in promoting disorder.Additionally,figure 6(b)showcases the thermal total dielectric susceptibility.The transition temperature values align with the peaks of the total dielectric susceptibility,withTtrvalues approximately ≈4,4.5,5.5,and 6.5 forEzvalues of 0.5,1,1.5,and 2 respectively.To synthesize the findings from figures 6(a) and (b),we present a graphical representation in figure 6(c),illustrating the correlation between the transition temperature and theEzparameter.In order to consolidate the results depicted in figures 6(a) and (b),we have included a graphical representation in figure 6(c) that illustrates the correlation between the transition temperature and the parameterEz.The figure effectively demonstrates that there was an almost linear increase in the transition temperature as the ferrielectric parameterEzis progressively elevated.
To complete the study,our focus is on scrutinizing the effect of temperature (T) on hysteresis loops,visualized in figure 7 with fixed parametersD=0,Jss=1,andJSσ=-0.01.As the temperature rises,the hysteresis loop maintains its singular nature,though its area contracts.Upon reaching a threshold temperature of 2,the loop vanishes,denoting the system’s transition from the ferrielectric to the paraelectric phases.This occurrence underscores the gradual evolution of the system into a paraelectric state with increasing temperature.
Furthermore,figure 8 portrays the influence of the exchange coupling parameterJSSon the hysteresis loop,with constantsJSσ=-0.01,T=0.1,andD=0.The system retains a singular loop structure.Yet,in contrast to the effect ofJSS,the loops change in area,coercivity,and saturation field asJSSvalues rise.This transformation arises due to the enhanced exchange coupling,imparting greater stability to the system.
In figure 9,we also examined the effect of the ferrielectric parameterJSσon the hysteresis cycles,plotted withD=0,Jss=1 andT=0.1 and by decreasing the parameterJSσ,the hysteresis cycles show multiple loops.The saturation also increases when decreasing the parameterJSσ.
To wrap up,we analyze the effect of the crystal field D on hysteresis loops,illustrated in figure 10 while maintaining constantsJss=1,JSσ=-0.01,andT=0.1.A reduction in theDparameter correlates with a reduction in the hysteresis loop’s size.Upon reaching a crystal field value of -7,the loop’s presence vanishes.This shift signifies the transition of the system from the ferrielectric to the paraelectric phases.
4.Conclusion
In this study,we utilized the MCt to explore the dielectric characteristics of a sulflower-like structure.The structure considered in our investigation consists of mixed spins(1,5/2).One of the main objectives was to determine and analyze the configuration of spin in the phase diagrams.Moreover,we examined dielectric characteristics of the system considering their dependencies on different physical parameters.Specifically,we investigated the impact of temperature,as well as external longitudinal electric on polarization,dielectric susceptibility,and hysteresis cycles.In summary,the findings demonstrate a linear decrease in transition temperature asJSSincreases,a corresponding increase in transition temperature with |JSσ|,and a clear linear rise in transition temperature with increasingEz.As temperature rises,the solitary hysteresis loop contracts and vanishes at 2,signifying the transition from ferrielectric to paraelectric phases.Maintaining a uniform loop structure,the system exhibits altered traits asJSSvalues increase,influenced by enhanced exchange coupling.Besides,decreasingJSσyields multiple loops and elevated saturation.Moreover,loweringDfurther contracts hysteresis loops,and a crystal field of -7 erases the loop,marking the ferrielectric to paraelectric transformation.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education(2020R1I1A3052258).This work is funded by Researcher Supporting Project number (RSP2024R117),King Saud University,Riyadh,Saudi Arabia.
Conflicts of interest or competing interests
The authors confirm that there are no known conflicts of interest associated with this publication.
Author contributions
Not Applicable
Data and code availability
This investigation was made using Monte Carlo simulations under the Metropolis algorithm by a Fortran code.
ORCID iDs
杂志排行
Communications in Theoretical Physics的其它文章
- Electrical characteristics of a fractionalorder 3 × n Fan network
- Theoretical study of the nonlinear forceloading control in single-molecule stretching experiments
- Diffusion of nanochannel-confined knot along a tensioned polymer*
- Two-component dimers of ultracold atoms with center-of-mass-momentum dependent interactions
- Phase structures and critical behavior of rational non-linear electrodynamics Anti de Sitter black holes in Rastall gravity
- Holographic dark energy in non-conserved gravity theory
