Diffusion of nanochannel-confined knot along a tensioned polymer*

Guobing Cai ,Yong Li ,Yuyu Feng ,Zhouhui Deng and Yanhui Liu,3

1 College of Physics,Guizhou University,Guiyang 550025,China

2 Kechuang Industrial Development Company Limited,Guian New Area,Guiyang 550025,China

3 State Key Laboratory of Public Big Data,Guizhou University,Guiyang 550025,China

Abstract The knots frequently occur in biopolymer and their diffusion plays an active role in the gene regulation.In this work,Langevin dynamics simulations were carried out to detect the diffusion behaviours of a knot along a tensioned polymer in different spatial constraints.The polymer accommodating a knot was tethered to two macrospheres to block the unravelling of the knot.As a result,the curves for the diffusion coefficients of the knot with different bending stiffness as a function of the tension in different spatial constraints were obtained.In the space without constraints or with weak constraints,the corresponding curves for the knot with relatively large bending stiffness exhibited two turnover behaviours.On the contrary,for the knot with relatively small bending stiffness,the diffusion coefficients were monotonically reduced with increasing tension.However,in a space with strong constraints,all the curves showed one turnover behaviour regardless of the bending stiffness.The turnover behaviours divided the curves into different regimes,and the dominant diffusion mechanisms in the regimes,namely,knot-region breathing,self-reptation,and internal friction,were clearly identified.The effective friction coefficients ξ of the knots with 31,41,51 and 52 types as a function of the knot size N at a fixed tension were well fitted by the relation ξ ∝N.The effective friction coefficients of the knots at relatively large tension f>3 sharply increased with the knot complexity,which is not dependent on the spatial constraints.By contrast,the values of these coefficients at relatively small tension f≤3 were remarkably dependent on the spatial constraints.Our work not only provides valuable simulation results to assist the understanding of the diffusion of DNA knot,but also highlights the single-molecule design for the manipulation of DNA knots in future.

Keywords: knot,langevin dynamics simulations,diffusion coefficient,self-reptation,knot-region breathing,internal friction

1.Introduction

Knots are frequently found to occur in biopolymers,such as DNA molecules and proteins,and directly affect the gene regulation mechanisms [1–4].For instance,knots can bein vivointroduced into cellular DNAin vivothrough processes such as DNA replication and regulated by enzymes such as type II topoisomerases which both knot and unknot DNA [3,4].Knots can be artificially introduced into linear DNA by using single-molecule techniques and are intentionally proposed as a braking mechanism to improve the temporal resolution of nanopore sequencing [5–7].In addition,the production of DNA knotsin vitrohas turned out to be a highly efficient manner to package mutant DNA into virus capsids [8].Due to its biological functions and biophysical significance,knotted DNA serves as a minimal system to study the diffusion mechanism of molecular knotting and knot theory as applied to polymer physics [6,9].

The emergence of nanochannel techniques is arising as a powerful tool to deeply understand the knot diffusion in polymer [10–17].In a series of experiments,one knot have been successfully introduced into a DNA molecule confined in a nanochannel and then stretched by an elongation force provided by divergent electric fields[18–21].The knot appeared in the fully extended DNA as a region with excess fluorescent brightness.Its motion as a function of the applied tension rate could be tuned from a mobile to a jammed state and the knot jamming is reversible.Under these conditions,knots can be driven towards the closest end of the DNA molecule and untied.After shutting off the electric fields,knot swelling over time was also observed [21,22].A recent single-molecule experiment based on optical tweezers successfully introduced knots into an individual DNA molecule and manipulated the knot with applied tension.From the reported results,it was indicated that these knots,highly localized under tension,remained surprisingly mobile and underwent thermal diffusion[9].The diffusion constants of the knots with different complexities were correlated with theoretical calculations concerning the knot sizes by using a simple hydrodynamical model of‘self-reptation’ of the knot along a polymer [9,13,14,23].Nonetheless,in another experiment based on nanochannel,it was reported that self-reptation was not the only mechanism responsible for the diffusion.More specifically,it was suggested that an additional mechanism,namely breathing of the knot region,which involved the local exchange of stored length with the vicinal chain,is expected to dominate in relatively large knots,significantly increasing the knot diffusivity with quadratic scaling of the diffusion time [6,10].

Motivated by the above-mentioned experimental results[9,13,14,19,21],a series of simulations were performed in this work to systematically study the diffusion of a knot along a tensioned polymer.From the acquired simulated outcomes based on Langevin dynamics,it was demonstrated that the knot diffusion coefficient was non-monotonically dependent on the tension at sufficiently large bending stiffness of polymer [24,25].However,the diffusion behaviours at low tension were not identified for the knot size comparable with the contour length of the polymer.At the same time,the underlying mechanism responsible for the diffusion of knots was clarified to better understand the physical processes enclosed in the experiments outlined in the above reviews.In the following simulations,the polymer confined in a nanochannel was tethered to macrospheres to prevent the unravelling of the knot from the polymer.Moreover,Langevin dynamics simulations were employed to detect the relationship of the various diffusion behaviours of a knot along a polymer in different spatial constraints as a function of the applied tension,especially at low tensions.

2.Materials and methods

2.1.Coarse-grained polymer model

Figure 1. (A)Schematic illustration of the simulation setup:the ends of a polymer chain with 500 beads accommodating a 52 knot(highlighted in purple) are anchored to a macrosphere held fixed in the origin (left) and to a mobile one pulled along the x axis with a force f=0.5.This simulation setup is confined in a cuboid nanochannel with length l,width a,and height a scaled by σ,and the length l is parallel to the x axis.(B) Typical conformations accommodating different knots (highlighted in dark blue).From up to down,the typical conformations represent a single knot 31,41,51,and 52,respectively.

As shown in figure 1(A),the simulation setup,which was composed of two macrospheres and a semi-flexible chain accommodating knots with different types,was confined in a cuboid nanochannel.This semi-flexible polymer was modelled by a coarse-grained bead-spring model,which was composed ofLmonomers of diameter σ and massm(σ andmare set as the unit of length and mass,respectively),and the contour length of the polymer used in current simulations is 500σ.Its two ends were tethered to two macrospheres,and the diameter of the two tethered macrospheres should be larger than the knot size to block the unraveling of the knot.

The interaction between two adjacent monomers in the semi-flexible polymer can be described by the finite-extensible nonlinear elastic (FENE) potential as follows

It is a harmonic potential with a bond potential ofkFENE=and a maximum degree of stretching ofR0=1.5σ.These parameters were taken from the standard polymer model of Kremer and Grest[26],andri,i-1=is the distance between any pairs of monomers.At the same time,the bending potential between two adjacent monomers can be introduced as follows

whereθi=denotes the angle between two adjacent bond vectors,andkrefers to the bending stiffness.The equationlp=κσ that correlates the persistence lengthlpwith the bond stiffness was applied to map the coarse-grained bead-spring model to dsDNA,and the parameters of hydrated dsDNA were adopted as σ=1.0 nm and κ=50kBT.

In addition,the spatial interactions between any two monomersiandjwere given by a short range truncated and shifted Lennard–Jones (LJ) potentialULJof strength ∊with a cutoff distancerc=[27]

where ε=kBTis the unit of energy,andkBandTdenote the Boltzmann constant and the temperature,respectively.

To identify the impact of confinement on the diffusion of the knot along the semi-flexible polymer under tension,the interactions between monomers and the nanochannel were described as follows:

wherediis the orthogonal distance between theith monomer and the nanochannel.Finally,the function ϑ(x) in equations(3)and(4)is the Heaviside function,can be defined as

2.2.Langevin dynamics simulations

During the dynamics,the macrosphere center and the chain ends were constrained to move along thex-axis [28].A constant forcewas also applied to the semi-flexible chain via two macrospheres,and the corresponding stretching potential was defined asUstretch==-fX.Thex-axis coincides with the direction of the forcef,andXis the projection ofon thex-axis.The adimensional,reduced forcefis typically varied in the range from 0.5 to 15 to characterize the mechanical tensile response of the knots under small,as well as large tensions.The model can explore a wide variety of polymer molecules with different values oflpranging from 1σ to 20σ,which correspond to polysaccharides and doublestranded DNA,and all of the simulations were performed at a constant temperature(T=).Since the macrospheres were free to rotate,and therefore no torsional stresses were generated in the simulations.The dynamics of the chain is generated by solving the Langevin equation as follows

whereUiis the total potential of theith monomer,including all the potentials mentioned above,and ξ0is the friction coefficient for each monomer and its value was set asξ0=,whereis the Lennard–Jones time.The Stokes friction equation for a spherical monomer is given by the following expression: ξ0=3πηsolσ,in which ηsolis the viscosity of the solution.For a specified water viscosity ηsol=1cP,T=300 K,and σ=1.0 nm,the characteristic Lennard–Jones time τLJare related to≈1.14 ns.In addition,is a stochastic force term that satisfies the fluctuation-dissipation theorem.Finally,the dynamical evolution of the system is numerically integrated with the LAMMPS package with an integration time step of 0.005τij∼5.7 ps,and the total simulation time is about 108τLJ.

2.3.Knot detection and analysis

From a mathematically rigorous point of view,knots are defined only for closed chains.For our analysis,it is crucial to extend the knot notion to open chains by introducing appropriate schemes for joining the ends of the open chain by an arc and turning it into a closed ring.After closure,the physical knotted state of an open chain can be established by using the Alexander determinants [29],and the knotted portion of a chain is finally determined as the shortest chain segment that maintains the topology of the whole chain.The shortest chain segment is measured and identified based on a bottom-up searching scheme,which consists of three steps:(i)compute the center of mass of the portion,(ii) construct two segments starting from the ends of the portion and going far away from the center of mass and(iii) connect the termini of these segments at ‘infinity’.Knots are designated byCk,whereCrefers to the minimal number of self-crossings displayed when the knot is projected into a plane,andkdenotes a cardinal index that is used to distinguish between topologically different knots with the sameC[30].In the current study,the Python package was employed to generate different knots.As shown in figure 1(A),a typical complex knot 51is accommodated in a polymer under tensionf=0.5,and the other simple knots 31,41,51,and 52are successively obtained,as demonstrated by figure 1(B).

3.Results and discussions

3.1.Impact of spatial constraints on the knot diffusion along a polymer

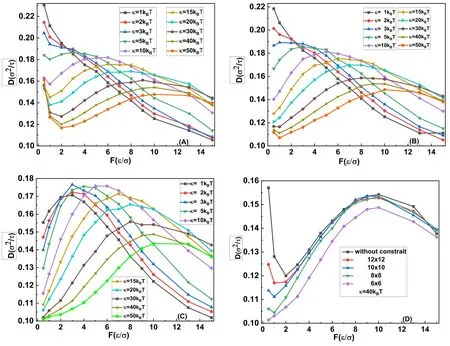
Figure 2. Impact of the spatial constraints on the diffusion coefficient of a 31 knot as a function of the tension f for different values of the bending stiffness κ.The spatial constraints corresponding to figures 2(A)–(C) are the space without spatial constraint,with 600×10×10,and with 600×6×6,respectively,and the contour length of the polymer is 500σ.(D) The diffusion coefficient of the 31 knot along a polymer with the bending stiffness κ=40kBT as a function of the tension f changes with the spatial constraints.

The diffusion of a knot along a polymer can be monitored by a discrete monomer indexn,known as the diffusion coordinate.As indicated by the conformation with a 31knot in figure 1(B),the boundaries of the knot region are defined asnlandnr,and the knot position along the chain is then defined asn=(nl+nr)/2.The knot diffusion coefficient can be identified by the following relationshipD=,where the square of the knot displacement[n(Δt)-n(0)]2is averaged over a series of short-time simulations,with the knot initially located atn(0) [25].In the current simulations,the unraveling of the knot from the polymer is prohibited by tethering its ends to two macrospheres.Therefore,the diffusion coefficient in the low-force limit can be extracted from the current simulations [28].According to this definition,the tension dependence of the diffusion coefficients of a knot with different bending stiffnesskunder different spatial constraints can be identified,and those of the 31knot are demonstrated in figures 2(A)–(D),in which the knot diffusion coefficients and tensionfare scaled by σ2/τ and ε/σ,respectively.Furthermore,the dependence of the diffusion coefficients of a 31knot along a polymer with the bending stiffness of κ=40kBTon the spatial constraint is outlined in figure 2(D),in which the curves for the space without constraints or weak constraints have two turnover behaviours,and the first turnover behaviour becomes totally disappeared in the space with a strong constraint of 600×6×6.

In the space without constraints and with weak constraints shown in figures 2(A) and (B),the diffusion coefficient of the 31knot as a function of the tensionfat relatively large bending stiffness κ>3kBTexhibits a non-monotonic pattern.Their corresponding curves have two turnover behaviours and are divided into three regimes,namely,the regime before the first turnover behaviour,the regime between the two turnover behaviours and the regime after the second turnover behaviour.Their corresponding knot diffusion coefficient is first reduced,and then increased,and finally decreased as the applied tensionfbecame bigger.Those at relatively small bending stiffness κ≤3kBTmonotonically decreased with the increasing tensionf.

In the regime before the first turnover behaviour,the diffusion coefficient of the 31knot reduced with increasing tension,which can be reasonably argued based on the knotregion breathing.Particularly,this effect involves the exchange of the stored length locally with the vicinal chain and is expected to dominate in large knots.The increasing tensionfgradually inhibits the knot-region breathing by reducing the knot size,consequently resulting in slower diffusion.This pattern is captured in figures 3(A)–(C),in which the relatively large knot in figure 3(A) is reduced to the relatively small one in figure 3(C) by increasing the tension from 0.5 to 2.When the knot conformation further developed into the loose knot corresponding to the regime between the two turnover behaviours (figures 3(D)–(F)),the 31knot selfreptated along the polymer under tension and its diffusion coefficientDincreased with the increasing tension.This effect could be interpreted considering that the knot diffusion is accomplished via a concerted motion of the loose knot.Hence,the total friction drag force that acts on the knot is proportional to the numberNof monomers within the knot multiplied by the friction coefficient ξ0per single monomer.Thus the friction coefficient ξ can be approximated asNξ0,and the Einstein relationD=kBT/ξ for a knot can be reexpressed asD≃kBT/Nξ0,The increasing tension could also effectively accelerate the knot diffusion by reducing the knot sizeN.

Figure 3. Typical conformations accommodate a 31 knot in a polymer under different tension in a space without constraints.(A)–(G)From up to down,the tension applied to the typical conformation with bending stiffness κ=50kBT is 0.5,1.0,2.0,5.0,7.0,10,and 15,respectively.(H)–(L)From up to down,the tension applied to the typical conformation with bending stiffness κ=1.0kBT is 0.5,1.0,2.0,5.0,7.0,10,and 15,respectively.

When the loose knot was switched to the tight knot corresponding to the regime after the second turnover behaviour,the intrachain interactions within the tight knot enhanced the ‘bumpiness’ of the energy landscape of the knot,which is the microscopic origin of internal friction[31–34].The application of a higher tensionfinduced a rougher energy landscape and consequently a slower diffusion.This assumption on the internal friction provided valuable insights for understanding the monotonic decrease of the diffusion coefficient of the 31knot with relatively small bending stiffness κ≤3kBTas a function of the increasing tensionfin the space without spatial constraints.As indicated by figures 3(H)–(J),because of the relatively small bending stiffness,the conformation of 31knot under tension is directly developed into the tight knot.For this reason,the diffusion coefficient was gradually reduced by the internal friction.

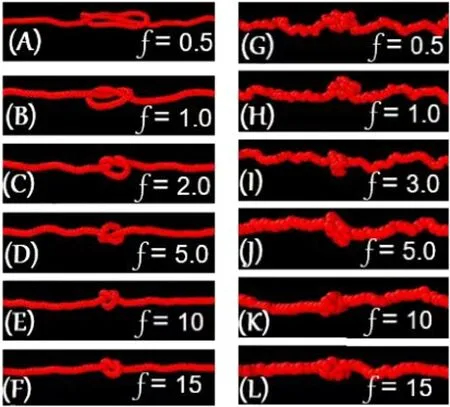
Figure 4. Typical conformations accommodating a 31 knot in a polymer under the application of different tensions in a space with the spatial constraint of 600×6×6.(A)–(F)From up to down,the tension applied to the typical conformation with bending stiffness κ=50kBT is 0.5,1.0,2.0,5.0,10,and 15,respectively.(G)–(L) From up to down,the tension applied to the typical conformation with bending stiffness κ=1.0kBT is 0.5,1.0,2.0,5.0,10,and 15,respectively.

In figure 2(C)with strong constraints of 600×6×6,the curves are divided into two regimes by the second turnover behaviour,namely,the regime before the second turnover behaviour,and the regime after the second turnover behaviour.In the regime before the second turnover behaviour,the change in the diffusion coefficient with the increasing tension could be ascribed to a similar assumption to that corresponding to the regime between the two turnover behaviours in the space without constraints or weak constraints(figures 2(A) and (B)).However,the conformation transition of the 31under the strong constraints of 600×6×6 is obviously different.As demonstrated by the typical conformations with large bending stiffness κ=50kBTin figures 4(A)–(F),the 31knot was compressed into the backfolding state (figure 4(A)) by the strong constraints.This effect resulted in the disappearance of the regime before the first turnover behaviour indicated in the space without constraints,namely,the knot-region breathing is inhibited by the strong constraints.The 31knot in the back-folding state and its successive loose knot(figures 4(A)–(F)) self-reptate along the polymer,and their diffusion is accelerated by reducing the number of monomers within this knot.As a result,its corresponding diffusion coefficients are increased.In the regime after the second turnover behaviour,the diffusion coefficient decreased with the increasing tension,which can be also reasonably understood by the internal friction in a tight knot.As indicated by figures 4(E)–(F),by increasing tensionfmore than 10,the 31knot switched from the transition state (figure 4(E)) to the tight knot (figure 4(F)).On top of that,the internal friction between the monomers within a knot,rather than the viscous friction due to the solvent,became gradually dominant over the knot diffusion,which induced the gradual reduction in the diffusion coefficients of the 31knot in the transition state and its following tight knot.The implementation of a higher tensionfreduced the diffusion of the knot,and even the 31knot was almost jammed in the polymer,which was observed in current simulations and recent single-molecule experiments [9].

The conformation transitions of the 31knot with relatively small bending rigidity κ≤3kBTin space with strong constraints of 600×6×6 were different from those with relatively large bending rigidity κ>3kBT.As indicated by figures 4(G)–(L),the typical knot conformations with bending stiffness κ=1kBTare directly developed into a loose knot by passing over the back-folding state,and then switched to the tight knot.Its corresponding diffusion coefficients first increased,and then decreased with the increasing tensionf.

Figure 5. The effective friction coefficient ξ varies dramatically with the knot size at different tension in different spatial constraints.The spatial constraints corresponding to (A)–(D) are without constraints,with constraints of 600×10×10,600×8×8 and 600×6×6,respectively.The applied tension ranges from 0.5 to 15 and the bending stiffness of knot is κ=50kBT.The symbols of ■,◦,◊,and ▲in different colors indicate the knots of type 31,41,51 and 52,respectively.

3.2.Effects of knot type on knot diffusion along a polymer

The diffusion coefficients for the knots with types of 31,41,51,and 52and different values of κ,funder different spatial constraints were systematically computed.The results for the bending stiffness κ=50kBTare outlined in figure 5,where the effective friction coefficients ξ=kBT/Dof the knots of type 31,41,51and 52as a function of the knot sizeNat a fixed tension were well fitted by the relationship ξ ∝N,where the ratio ξ/Nrepresents the friction coefficient ξ0of a single monomer [9,25].Moreover,some physical information enclosed in the knot diffusion can be drawn from the comparison among figures 5(A)–(D).More specifically,the effective friction coefficients of knots of type 31,41,51and 52as a function of the knot sizeNat relatively large tensionf>3 sharply increased with the knot complexity,which is not obviously dependent on the spatial constraints.By contrast,the effective friction coefficient ξ of knots with 31,41,51and 52types as a function of the knot sizeNat relatively small tension changing with the knot complexity is remarkably dependent on the spatial constraints.Take the relatively small tensionf=0.5 for example,in the space without constraints,the effective friction coefficients with 31,41,51and 52types as a function of the knot sizeNslightly increased with the knot complexity.With the gradual shrinking of the spatial constraints from 600×10×10 to 600×8×8,and then to 600×6×6,their corresponding effective friction coefficients of knots with types of 31,41,51,and 52as a function of the knot sizeNwere obviously reduced,then slightly decreased,and finally sharply increased with the knot complexity.All these effects can be attributed to knot-region breathing and internal friction.

4.Conclusions

In this work,the Langevin dynamics simulations were employed to detect the diffusion behaviours of a knot along a tensioned polymer in different spatial constraints.Motivated by the optical tweezers experiment,the polymer accommodating a knot was tethered to two macrospheres,so that the unraveling of the knot from the polymer could be prohibited.According to this simulation design,not only the diffusion coefficient of the knot at different tensions was obtained including the low-tension limit,but also the diffusion mechanisms,namely,knot-region breathing,self-reptation,and internal friction.

The spatial constraints had an obvious impact on the diffusion of a knot as a function of tensionf.In the space without constraints,the curve for the diffusion coefficients of a knot as a function of the applied tensionfat relatively large bending stiffness κ>3kBTwas divided into three regimes by two turnover behaviours,and the knot-region breathing,selfreptationf.Because of the relatively small bending stiffness κ≤3kBT,the knot was directly shrunk to a tight knot by the increasing tensionf,and the internal friction began to dominate the diffusion of a tight knot and resulted in the monotonically reduced diffusion coefficients with increasing tensionf.When the space was shrunk to the strong constraint of 600×6×6 from the space without constraints,the curve for the diffusion coefficient of a knot as a function of tensionfwas divided into two regimes by the second turnover behaviour,where the self-reptation and internal friction were separately responsible for the increasing and decreasing of the diffusion coefficients of knot with the increasing tensionf,and the knot-region breathing corresponding to the regime before the first turnover behaviour was inhibited by the strong spatial constraints,where the relatively large knot was compressed into the back-folding state,and then further shrunk with the increasing tensionf,self-reptating along the polymer.

The effective friction coefficients ξ of the knots with 31,41,51and 52types as a function of the knot sizeNat a fixed tension could be well fitted by the relationship ξ ∝N.Moreover,the effective friction coefficients of the knots with 31,41,51and 52types as a function of the knot sizeNat relatively large tensionf>3 sharply increased with the increasing knot complexity,which is not obviously dependent on the spatial constraints.By contrast,the effective friction coefficient ξ of the knots with 31,41,51and 52types as a function of the knot sizeNat relatively small tensions changing with the knot complexity is remarkably dependent on the spatial constraints.All of which can be attributed to knot-region breathing and internal friction.

The above simulation results for polymer with bending rigidityk=50kBTand σ=1.0 nm could be mapped to dsDNA,and their corresponding results in strong spatial constraint with 600×6×6 (figure 5(D)) demonstrated that the knot self-reptated along the dsDNA and its diffusion coefficientDincreased with the applied tensionffrom 0.5 to 10.0 pN,at the same time,the effective friction coefficient ξ of knots with different complexity increased dramatically with their increasing knot size at a fixed tension.The strong spatial constraints used in current simulations are reasonably compared with the experiment conditions used in a recent single-molecule experiment in reference [9],in which the λ genomic DNA accommodating an individual knot was confined in a space with 6%(w/v)poly(ethylene glycol)(PEG,molecular weight 35 000) and manipulated by optical tweezers with the applied tension ranging from 0.1 to 2.0 pN.Under these conditions,although the knot became highly localized,it remained surprisingly mobile and underwent thermal diffusion with classical random walk statistics.The single-molecule experiment results indicated that the effective friction coefficient ξ of knot with different complexities correlated with theoretical calculations of knot sizes and this correlation can be addressed by a simple hydrodynamical model of ‘self-raptation’ of the knot along a dsDNA.Obviously,the simulation results are consistent with the single-molecule results in reference [9],these consistencies not only assists the understanding of the diffusion of knot along a dsDNA,but also highlights the single-molecule design for the manipulation of DNA knots in the future.