基于北斗/GNSS-R的厘米级水位测量

张光霁 匡翠林 戴吾蛟 李新刚 包泽宇

（1.中南大学地球科学与信息物理学院，长沙 410083；2.中国空间技术研究院，北京 100094）

0 引 言

水位变化信息是防汛抗旱、水资源管理及全球气候变化研究的重要数据之一。目前由全球变暖造成的极端天气事件和洪涝灾害愈发频繁[1-2]，为保护人类的生命财产和环境安全，进行高精度的水位变化监测，制定洪涝或干旱等自然灾害的预警和应急措施变得愈发重要[3]。传统的水位变化监测主要是利用水尺、水位计获取水位信息，但该方法存在易受地面沉降影响、监测成本较高等缺点，且恶劣的气象条件可能导致观测仪器破坏[4-5]，无法提供有效的水位变化数据。随着全球导航卫星系统（Global Navigation Satellite System，GNSS）技术的不断发展，GNSS 反射测量（Global Navigation Satellite System-Reflectometry，GNSS-R）作为一种新型遥感技术具有低成本，信号源丰富，能进行全天时、全天候观测等诸多优点[6-8]，已应用于海面测高[9-10]、土壤湿度测量[11]、海风探测[12]等领域。北斗卫星导航系统（Beidou Navigation Satellite System，BDS）作为中国自主发展、独立运行的卫星导航系统，在BDS 反射测量（Beidou Navigation Satellite System-Reflectometry，BDS-R）应用方面潜力巨大。Jin等[13]首次将BDS应用于海面高度反演，对BDS三频信噪比（Signal-to-Noise Ratio，SNR）数据的反演能力进行了研究，其反演结果与验潮站实测结果的相关性为0.83～0.91，均方根误差（RMSE）小于0.6 m，初步验证了BDS 在GNSS-R 应用中的可行性。Zheng 等[14]通过分析多频多模GNSS-R 水位反演结果，证实了BDS2-MEO 的监测精度优于BDS2-IGSO，BDS3-MEO 的监测精度与BDS2-MEO相当。Deng等[15]研究了低成本BDS-3在水面测高应用中的可行性，实验结果证明BDS-R的性能可通过混合星座得到显著提高，表明了BDS 在GNSS-R 应用中具有巨大潜力。

目前基于SNR数据的GNSS-R 水位反演方法有2 种。一种是利用Lomb-Scargle频谱（Lomb-Scargle Periodogram，LSP）分析的方法提取SNR振荡中的反射高信息，该方法反演结果依赖于卫星弧段，输出结果在时间分布上不均匀，且易受随机噪声的影响[16]。另一种是由Strandberg 等[17]提出的非线性拟合方法，该方法利用B-样条曲线表达水面变化，通过非线性拟合法确定对应的B-样条系数，该方法得到的结果拥有更高的精度。

本文基于在湖南省浏阳河流域建设的GNSS-R 实验站，利用LSP 分析方法和非线性拟合方法对不同系统的水位反演精度进行分析评估，并进行多系统数据融合，探索北斗/GNSS-R 厘米级水位监测能力，进一步挖掘BDS 在水位监测中的潜力。

1 GNSS-R水位测量原理及方法

1.1 GNSS-R水位测量原理

GNSS-R 水位测量几何原理如图1 所示。GNSS 卫星发射的信号到达水面后发生反射，其相位、振幅、传播方向等发生了改变。变化后的反射信号中携带了地表地物信息再到达接收机，与直射信号发生叠加或干涉。

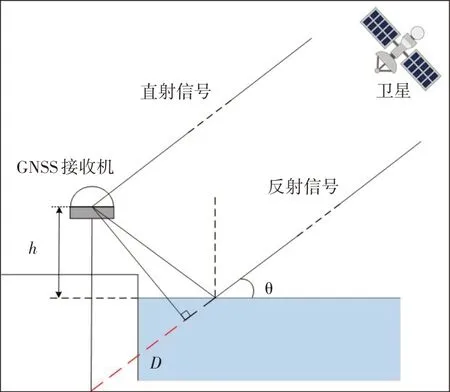
图1 GNSS-R水位测量几何原理

从图中可知，直射信号与经水面反射后的信号之间的路径差D可表示为：

式中：h为反射高度，θ为卫星高度角。

由此可得，直射信号和反射信号之间的相位差为：

式中：λ为卫星信号波长。

由式（2）可推得频率为：

因此，接收机与水面的垂直反射高可表示为：

GNSS-R 水位测量主要利用GNSS 接收机中的SNR数据。直射信号与反射信号之间的干扰在GNSS 接收机中记录为SNR数据。SNR可表示为：

式中：PR为信号功率；N为噪声功率。

SNR与干涉后合成信号的振幅间满足如下关系：

式中：Ac为合成信号的振幅；Ad为直射信号振幅；Am为反射信号振幅。

大地型GNSS接收机为了有效抑制多路径效应引起的误差，其直射信号的振幅远大于反射信号的振幅，因此多路径效应对SNR的影响很小。通过低阶多项式拟合去除趋势项，消除SNR中的直射信号部分，去除趋势项后，可将多路径效应建模为：

δSNR=Acos(2πfsinθ+φ) （7）

式中：δSNR为去趋势项的信噪比数据；A为振幅；φ为相位。

由式（7）可知，GNSS-R 水位反演就是对δSNR进行分析，求解其频率f，即可由式（4）算得反射高h。LSP 分析和非线性拟合是两种求解h的常用方法。

1.2 频谱分析方法

LSP分析方法作为一种分析时间序列数据中周期性信号的统计工具，适用于处理非均匀采样的数据。相比于傅里叶变换等方法，LSP分析方法更具灵活性，能够处理实际观测中时间间隔不规则的数据。该方法将频率对应的功率定义为：

式中：Xj为离散实验数据，即去趋势项后的SNR数据；tj为数据对应的高度角正弦值；τ为时间延迟项，可定义为：

式中：ω= 2πf。

通过频谱分析找到峰值频率f，便可利用式（4）求出对应的反射高度，即可得出接收机天线距离水平面的垂直距离h。图2为去趋势项后的SNR信号及对应的Lomb-Seargle周期图，为确保峰值频率的可信度，通常会引入阈值和峰噪比2个质量控制参数，峰噪比定义为：

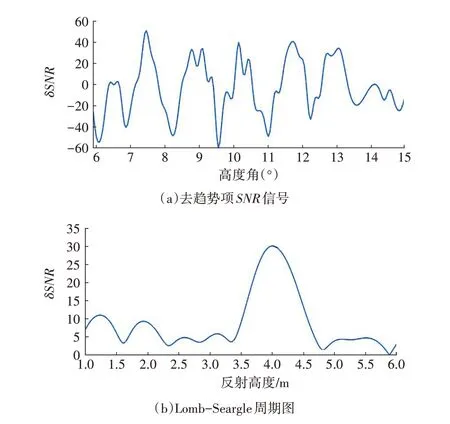
图2 去趋势项SNR信号及Lomb-Seargle周期图

式中：Ppeak为峰值功率；Pmean为平均功率。

周期图中功率低于阈值的部分将被视为背景噪声，而峰噪比能够有效抑制多峰情况导致的结果偏差。

1.3 非线性拟合方法

非线性拟合方法是由Strandberg 等[17]提出的，该方法在式（7）中引入了一个用于描述由于表面粗糙度引起的相干性损失的衰减因子：

式中：k为波数；s为反射面的粗糙度参数。

添加衰减因子后，将SNR振荡信号建模为：

式中C1与C2用于替换振幅A与相位φ。振幅A与相位φ可由下式进行转换：

Strandberg 等提出，LSP 分析方法得到的结果不连续，无法有效反映水位变化的时间序列，因此引入B-样条曲线表达长期的连续水位变化。B-样条曲线是一种用于平滑曲线的数学曲线模型，具有良好的局部控制性、平滑性和灵活性，零阶的B-样条基函数可表达为：

高阶的B-样条基函数可由式（15）递归计算获得：

式中：ui为B-样条曲线的节点；p为样条曲线的阶数。

大多数应用中通常使用二阶或三阶B-样条曲线，本文中采用二阶B-样条曲线。由基函数可将反射高拟合为：

选取m个采样点作为B-样条曲线节点来拟合函数y=f(x,t)，其中x为待定系数，且x=(x1,x2,…,xn)(n＜m)。对于非线性最小二乘问题，第i次观测的残差可表达为：

式中：yi为SNR振荡信号。

通过最小二乘法求解最优参数集使得所有观测残差的平方和最小：

在本方法中，待定系数为振幅A，相位φ，频率f，粗糙度参数Λ=s2。本文采用高斯—牛顿算法处理非线性最小二乘问题。高斯—牛顿算法是非线性回归模型中求回归参数进行最小二乘的一种迭代方法，其基本思想是使用泰勒级数展开式近似地代替非线性回归模型，然后通过多次迭代，多次修正回归系数，使回归系数不断逼近非线性回归模型的最佳回归系数，最后使原模型的残差平方和达到最小，最后得到最佳拟合的频率f，进而依据式（4）求出反射高度。

2 实验及结果分析

2.1 实验数据采集

为验证北斗/GNSS-R 的厘米级水位监测能力，本文基于建设在湖南长沙雨花区浏阳河流域㮾梨水文站旁的GNSS-R 实验观测站数据开展实验。该观测站于2023 年10 月25 日建成，接收机型号为BYNAV C1，天线型号为NOV-BY352P。本观测站接收GPS、俄罗斯格洛纳斯卫星导航系统（GLONASS）、欧洲伽利略卫星导航系统（Galileo）、BDS的数据，接收的信号频段如表1所示。

表1 接收机接收信号频段

图3 为浏阳河GNSS-R 观测站现场图，图中右侧红圈处为观测站所处位置。本次实验利用距观测站约100 m 处㮾梨水文站（图中左侧红色方框处）提供的实测数据作为验证参考数据。

图3 浏阳河GNSS-R实验观测站

根据观测站现场情况，考虑建站难度及观测区域大小，将观测高度角限制为4°～15°，方位角范围限制为65°～200°，对应的菲涅尔反射区如图4所示。本文实验数据采用的时间段为2023年12月1—20日，接收机采样间隔设置为30 s。

图4 GNSS-R观测站菲涅尔反射区

2.2 LSP分析方法结果与分析

将不同系统的观测数据进行频谱分析，并将反演结果与水文站实测水位数据进行对比分析。图5、图6 为不同系统采用LSP 分析方法的反演结果与水文站实测水位的对比及相关性分析图。通过对比各系统反演结果可以看出，虽然LSP 分析方法反演的水位中有部分结果出现了偏离实测水位的情况，但整体趋势符合水位实际变化情况，RMSE都在厘米级，且均保持在6 cm 左右（表2）。4 个系统的反演与实测水位相关系数均大于0.9，证明LSP分析方法的反演结果能够较好地反映水位变化，其中BDS的相关系数最高，充分证明了BDS在水位反演中能够有效表达水位随时间的变化情况。

表2 LSP分析方法水位测量精度统计结果

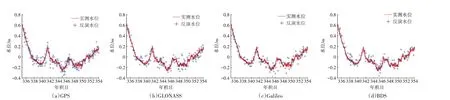
图5 各卫星系统LSP分析方法反演水位与实测水位对比

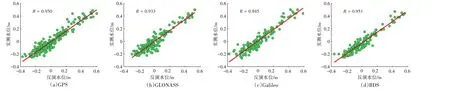
图6 各卫星系统LSP分析方法反演水位与实测水位相关性分析

由于单系统反演结果不具有连续性，因此本文组合多GNSS 系统进行LSP 反演，并利用3 次样条曲线进行拟合，再次与实测水位进行对比，图7 为结果对比图及相关性分析图，可以看出将该方法反演结果进行简单拟合，反演结果的精度提升到了5 cm以内，该方法能有效提高反演结果的时间分辨率，能够更清晰地表达水位随时间的变化。

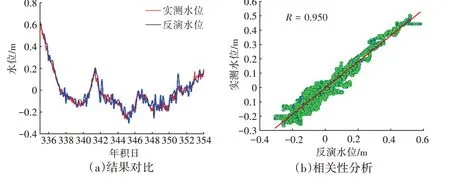
图7 LSP分析方法多GNSS系统组合结果

从结果上看，由于实验场地在城市区域，高度角范围设置在4°～15°，在一定程度上限制了观测数据量，导致单系统的反演结果分布不均且精度较低，通过将多GNSS 系统数据组合进行样条曲线拟合的方法能够有效提高LSP反演结果的精度与时间分辨率。由于只是简单地进行数据组合，在缺少反演点的位置可能会出现振荡，稳定性有所欠缺。总体而言，LSP方法的水位反演结果与实测水位具有良好的一致性。

2.3 非线性拟合方法结果与分析

非线性拟合法的结果依赖于B-样条曲线节点的时间间隔，在数据频率较高的情况下可选取更多节点以提高反演精度，而对于低频数据应选择更长的时间间隔。考虑到场地限制，避免初始反演点数量不足的情况，本文实验设置节点选取时间间隔为5 h。图8、图9为不同系统采用非线性拟合法得到的反演结果与水文站实测水位的对比及相关性分析图。

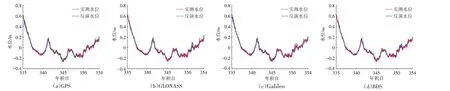
图8 各卫星系统非线性拟合法反演水位与实测水位对比

图9 各卫星系统非线性拟合方法反演水位与实测水位相关性分析

从结果来看，GLONASS 的反演结果仍略差于其余系统，出现这种情况可能是由于GLONASS 的各频段频率较低，而波长较长的信号受多路径效应影响更小，因此接收机中记录的SNR 信号所包含的信息较少，从而降低了水位反演的准确性[18]。GPS 和BDS 在反演结果精度最高，相关系数优于其余系统，在水位变化反演中表现出了出色的性能。各系统采用非线性拟合法的水位反演结果与水文站实测水位的相关性均达到了0.99 以上，拟合效果较好，且通过B-样条曲线的拟合，在水位变化的结果表达上也更加平滑和精确，能够提供高精度、高时间分辨率的水位监测结果。与LSP 分析方法的反演结果相比，非线性拟合法反演结果的精度得到大幅提升，RMSE 降低到2 cm 左右，平均提高了4.1 cm，精度提高了66%左右（表3）。

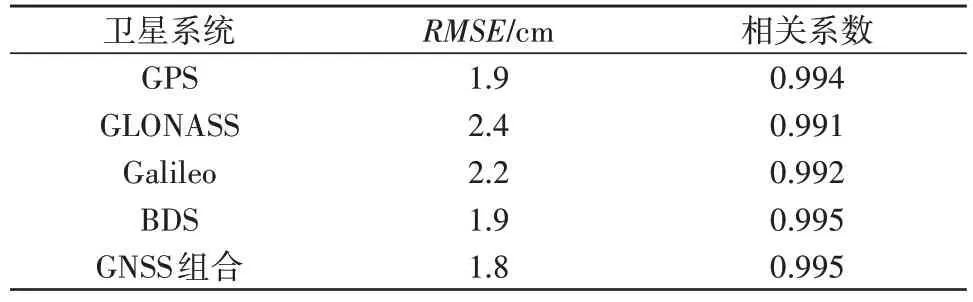
表3 非线性拟合水位测量精度统计结果

对于非线性拟合法，同样将多GNSS 系统组合进行实验，多GNSS系统组合能够提供更好的空间和时间覆盖，进而提供更多初始观测值，B-样条曲线的初始节点选择时可采用更小的时间间隔，增加反演结果的准确性和可信度。图10 为多GNSS 系统组合后的反演结果及结果相关性分析，其精度得到了小幅提高，水位反演结果与实测水位变化十分吻合，且未出现振荡或明显的拟合错误，该方法得到的水位反演结果与实测水位相关性达到了0.99以上。总体来说，不论是LSP分析方法还是非线性拟合法，BDS在水位监测中都可得到高精度反演结果并表现出了良好的稳定性，其结果与水文站实测数据相比都具有良好的一致性。

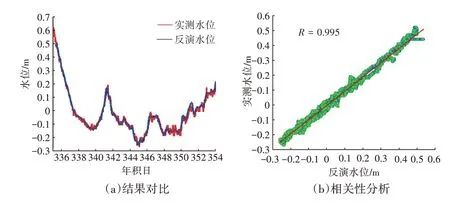
图10 非线性拟合法多GNSS系统组合结果

3 结 语

本文基于浏阳河试验场的GNSS-R 实验站观测数据，通过对比不同卫星系统的反演结果，系统评估了我国BDS在GNSS-R 水位反演中的性能。通过对比LSP 频谱分析法和非线性拟合法两种方法的反演结果，验证了GNSS-R 水位监测技术即使在实验场地受限的情况下仍可获得厘米级精度，且非线性拟合法能够大幅提高水位反演精度，相较于LSP 方法精度提高了约66%左右。BDS 在GNSS-R 水位测量中的精度整体与GPS 相当，验证了BDS 在GNSS-R水位反演中的优越性能，能够为洪涝干旱等自然灾害的预警防范提供技术支持，扩展了BDS 的应用场景。