并列切角方柱风致干扰效应的大涡模拟研究
2024-05-08李方慧张智博张特范佳红尚靖淳
李方慧, 张智博, 张特, 范佳红, 尚靖淳
(黑龙江大学 建筑工程学院,黑龙江 哈尔滨 150080)
随着建筑物的密集程度增加,建筑间的干扰问题日益突出。此类问题导致建筑表面风压分布变化,进而影响围护结构的安全性甚至导致结构整体破坏。英国渡桥电厂下游冷却塔破坏[1]和美国汉考克大楼围护结构脱落[2]均由风干扰效应产生,可见对建筑间的风压干扰效应应该给予足够的重视。
早期的风荷载研究主要基于单体建筑为研究对象[3-8],逐步扩展为多建筑间的干扰效应研究。Gu[9]对不同排列下建筑的风压干扰效应进行研究,结果表明并列工况的放大效应尤其严重。谢壮宁[10]、朱剑波[11]、刘慕广[12]、Mara[13]基于高频测力天平风洞试验,归纳2个高层建筑不同空间位置下的气动干扰效应,并总结出建筑干扰包络图与干扰因子规律曲线。Yu等[14-16]系统对比了2栋不同高度的高层建筑间的扭转干扰效应和加速度干扰效应,发现高度比为1.0和1.5时,受扰建筑的基底弯矩增大作用最显著。Hui[17-18]分析了方形建筑与矩形建筑(长宽比为3)间的干扰效应,结果显示方形建筑的平均和脉动扭矩可分别达到单体状态的3倍和1.6倍,建筑角部的最小极值压力比单体方柱高40%。Yan[19-20]采用计算流体力(computational fluid dynamics)数值模拟方法,对城市中心高层双塔间的风荷载、风致振动和气动干扰效应进行了研究,并提出了基于刚度映射算法的高层建筑风效应及舒适度评估分析框架。
针对方形与矩形建筑间的干扰效应,国内外学者取得了一定研究成果,但对切角截面建筑考虑较少,而实际工程中,切角处理的建筑并不少见。文献[21]表明,切角能够大幅改善结构的气动性能。当切角率为10%时,建筑横风向和顺风向的风致位移响应能减少35%左右[22-23]。采用切角处理的建筑周围分离涡的数量、形态及其尺寸均发生了明显改变[24],进一步导致建筑间的气动干扰效应和风压干扰效应存在差异[25-27]。基于此,本文采用大涡模拟方法,对均匀流场下的三维方柱进行网格收敛性分析和模拟方法的验证,并基于切角方柱的气动力系数与风压分布特征,分析不同间距下并列双切角方柱的气动力系数变化特点和干扰因子分布规律。
1 大涡模拟及数据处理方法
1.1 大涡模拟
在结构抗风研究中,流体被视为黏性不可压缩,假定过滤过程和求导过程可以互换,将N-S方程做过滤,得到大涡模拟的控制方程为:
(1)
(2)

本文采用Dynamic Smagorinsky亚格子模型:
(3)

1.2 计算域及网格划分
计算域及模型尺寸见图1,方柱边长为L=0.1 m,竖向高度为4L,切角对应直角边长D=λL,λ=0.1。计算域大小为40L(流向x)×(20L+B)(展向y)×4L(竖向z),B为两方柱中心间距。网格采用非均匀结构化网格,采用加密处理的近壁面网格如图2所示,最小网格高度为5×10-4L,网格总数控制在150万~200万。计算域边界条件如图3所示,入口为速度入口(velocity-inlet),采用风速为U0的均匀来流;出口为压力出口(pressure-outlet);上、下表面以及两侧面均采用对称边界条件(symmetry)模拟自由滑移壁面;方柱表面采用无滑移壁面(wall)。压力速度耦合采用SIMPLEC法求解,动量方程采用二阶精度的离散格式。

图1 计算域尺寸Fig.1 Computational domain size

图2 近壁面网格划分Fig.2 Near-wall mesh generation

图3 计算域网格及边界条件Fig.3 Computational domain grids and boundary conditions
1.3 数据处理方法
为了便于结果对比,对文中出现的表面风压、升力和阻力均进行无量纲化处理:
(4)
(5)
(6)

采用峰值因子法估算各测点的极值风压系数:
(7)
式中:σp为测点风压系数的标准差;g为峰值因子。
对于峰值因子的取值,在GB 50009-2012《建筑结构荷载规范》中,假设结构满足高斯分布,建议g取2.5,置信率可达99.38%。但实际上,结构存在非高斯区域,在满足规范所要求的保证率下,峰值因子取值会增大。本文采用观察极值法和全概率迭代法结合计算峰值因子,置信率为99.50%。
为了更直观地表示方柱间的干扰效应,根据风压分布情况将方柱每个立面分为9个区域,切角从A~D编号,如图4所示。采用各区域测点极值风压系数的最大值作为各区域的极值风压系数,引入块干扰因子BIF0来描述方柱的干扰大小:

图4 测点布置与立面分块Fig.4 Sketch of tapping location and blocking region of facade
(8)

考虑到由于切角测点分布较少,采用BIF0并不能准确的描述角部干扰的分布规律,进一步采用测点风压系数干扰因子IF0进行分析:
(9)

2 网格收敛性分析与结果验证


表1 网格收敛性分析与结果对比Table 1 Analysis of grid convergence and comparison of results
为了进一步验证Case3网格的精确性,对比Case3模拟结果与文献[7-8]结果的平均风压系数(图5)和脉动风压系数(图6)曲线,模拟结果与文献结果的2种曲线吻合。
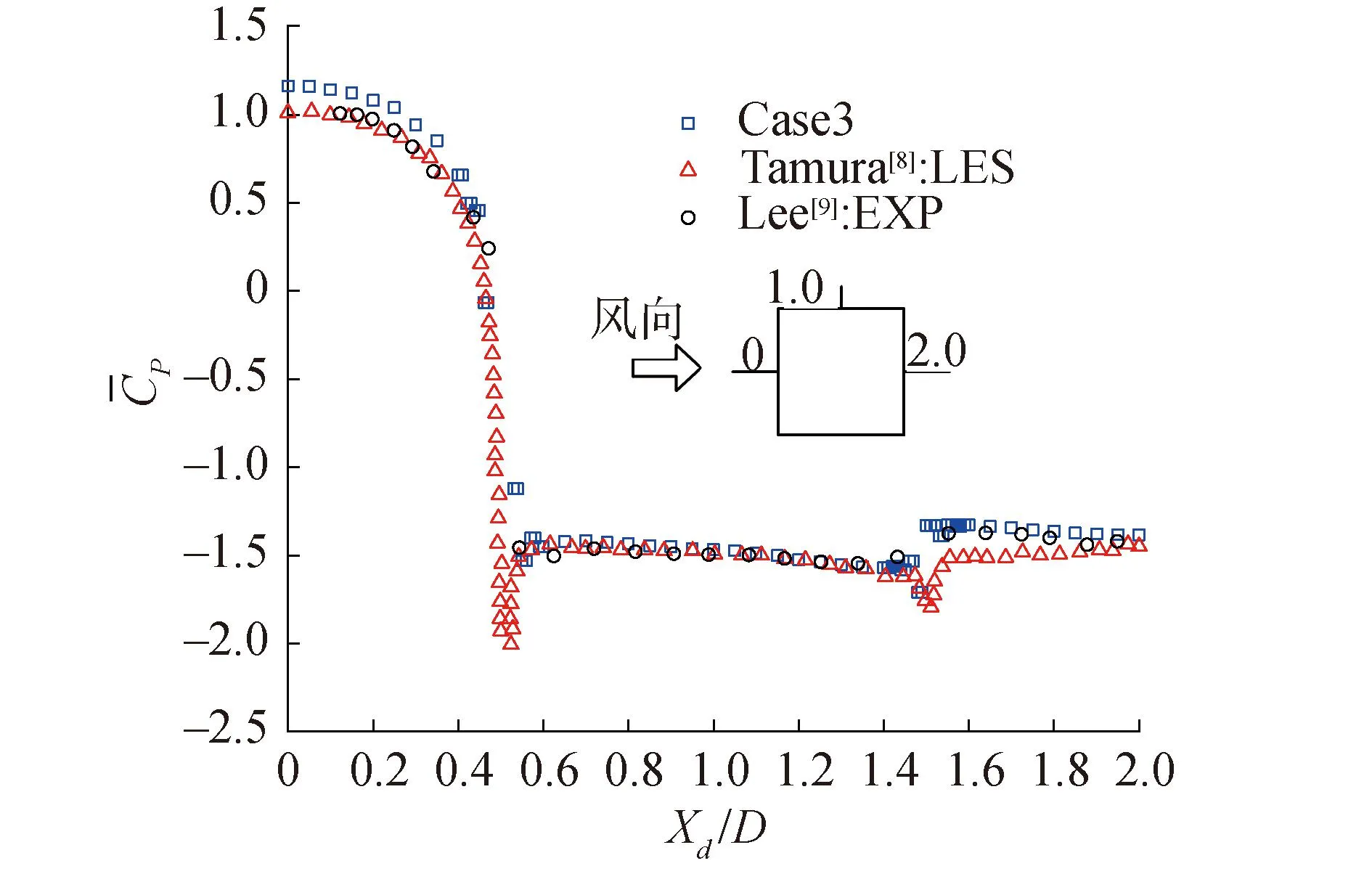
图5 平均风压系数比较Fig.5 Comparison of average wind pressure coefficients
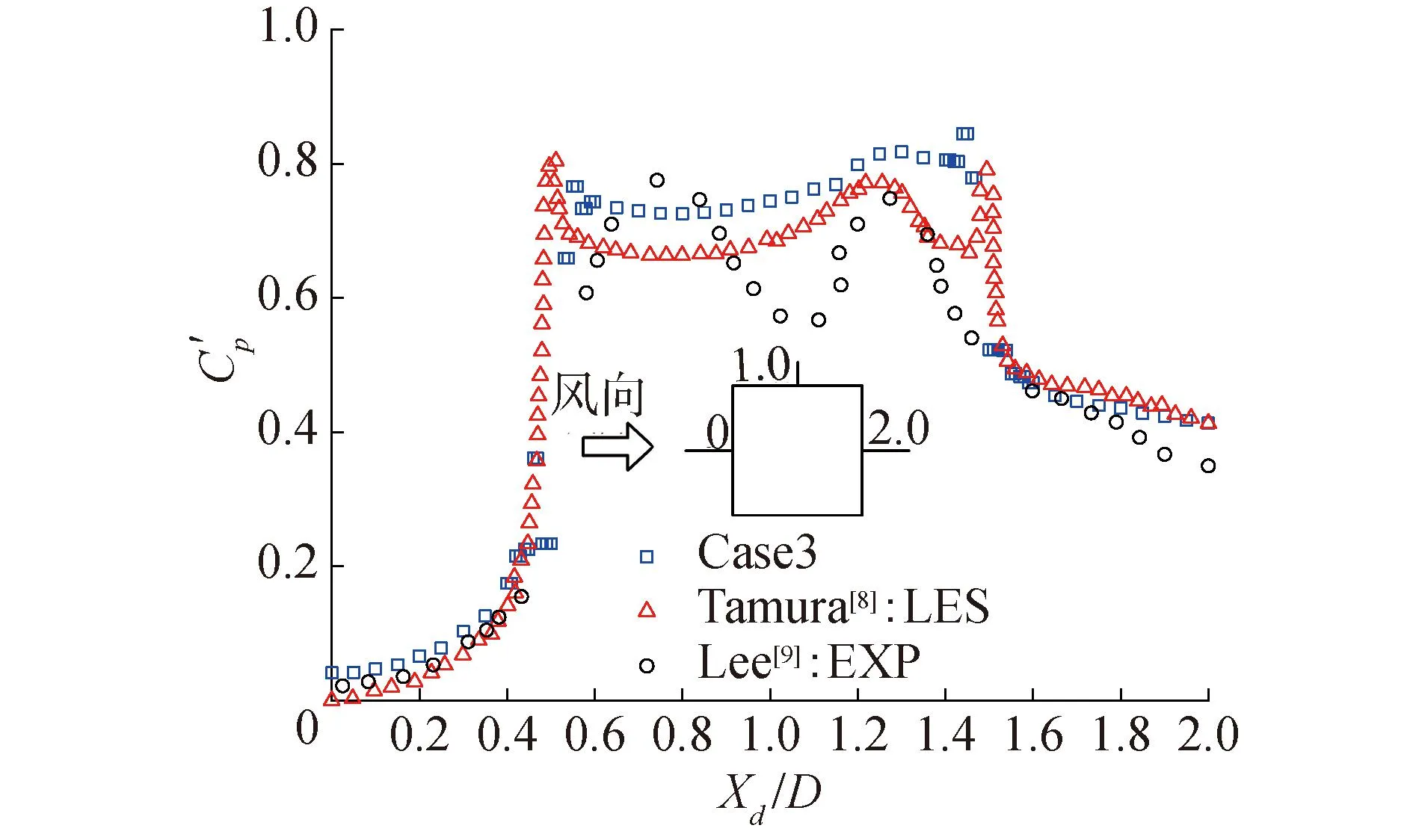
图6 脉动风压系数比较Fig.6 Comparison of fluctuating wind pressure coefficients
数值模拟的平均风压系数与文献值最大偏差不超过3%,对于脉动风压系数来说,本文对迎风面和背风面的模拟结果与文献结果相差不超过5%,但方柱侧立面的模拟结果平均值与文献[8]试验值相比大13%,产生这些差距的原因是因为数值模拟是在理想条件下进行的分析,而在试验过程中,会有影响试验结果的因素,如模型缩尺比、入流风场的精度等。综合上述的对比结果,整体的大涡模拟结果能够比较精确地反应方柱的各项气动力数值和风压结果,表明本文的网格模型与参数取值具有良好的精确性和可靠性。
3 干扰效应的结果与讨论
3.1 气动干扰效应
图7给出了方柱1和方柱2的气动力系数随间距比的变化曲线,由图7可见:
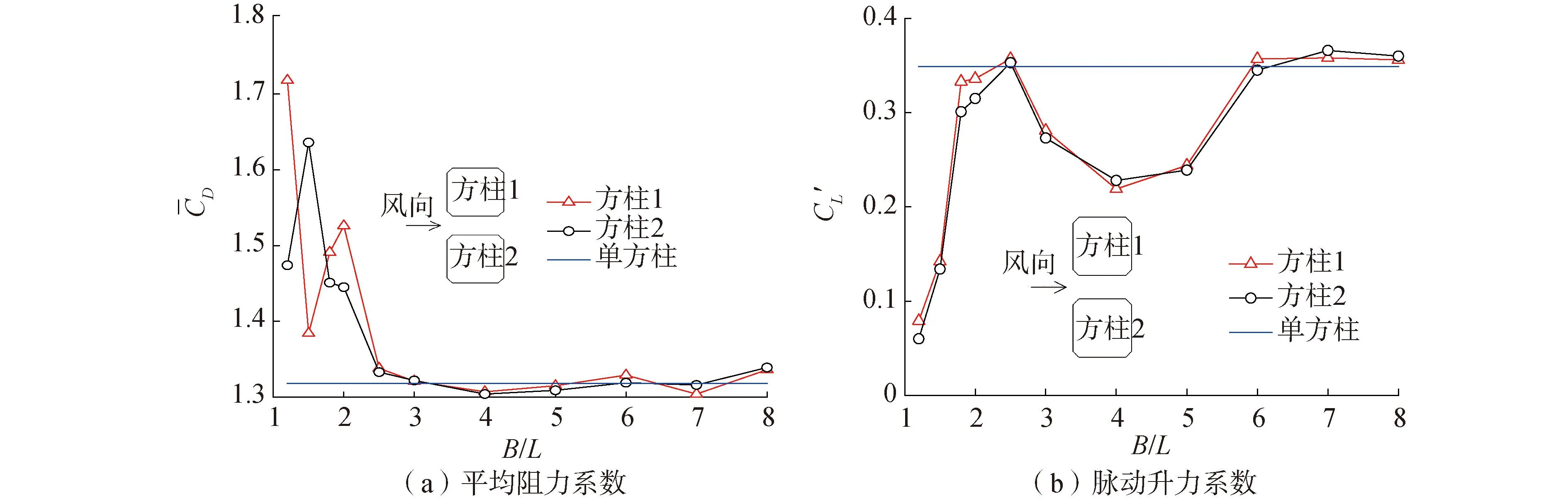
图7 气动力系数随间距比的变化曲线Fig.7 Aerodynamic coefficients vary with spacing ratio
1)当1.2≤B/L<2.5时,两方柱的平均阻力系数无规律波动且数值相差较大,说明此时流场仍然处于偏流状态。B/L=1.5时,两方柱系数差值最大,达到18%,间距比接近2.5时,系数趋于单体值。当2.5≤B/L≤8.0时,两方柱的平均阻力系数基本相同,与单方柱的值相比偏离程度不超过2%。
2)当1.2≤B/L<2.5时,两方柱的脉动升力系数逐渐增大并趋近于单方柱的值,脉动升力系数表现为减小效应。当2.5≤B/L<6.0时,两方柱的脉动升力系数先减小后增大,最小值为0.22,出现在B/L=4.0处,脉动升力系数依然为减小效应。当6.0≤B/L≤8.0时,双方柱脉动升力系数趋近于单方柱的值,最大误差为3%。总体来看,两方柱的脉动升力系数相差很小,变化规律一致。
3.2 流场分布
为了更直观地分析流场分布特点,图8给出了典型间距比下双切角方柱的流场分布图。当B/L=1.2时,2个切角方柱后壁面各出现一个贴近壁面的小尺度涡,尾流通过间隙形成一个大尺度涡,旋涡脱落后随尾流逐渐消失,小尺度涡的形成主要是由于切角的存在使剪切流变窄,剪切流遇到大尺度涡后产生回流,使涡旋更贴近壁面,此时处于偏流状态。当B/L=1.5时,后流场大尺度涡消失,转变为小尺度涡的脱落,流场中可以明显观察到小尺度涡有融合为大尺度涡的趋势,流场向稳态转变。当B/L≥2.0时,尾流状态转为对称涡,2个方柱的后流场互相干扰减小。
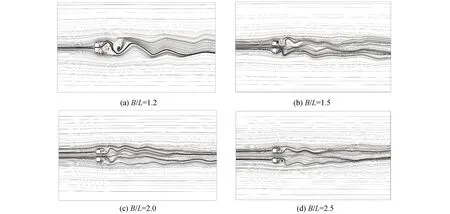
图8 不同间距下流场分布Fig.8 Flow field distribution at different spacing
3.3 并列切角方柱的风压干扰效应
由于并列双切角方柱沿流向的对称性,将方柱1考虑为施扰建筑,方柱2为受扰建筑,方柱1与方柱2间的位置关系见图1。
3.3.1 相邻立面(左立面)
方柱2的左立面即施扰建筑的相邻立面,左立面随距离的干扰因子(IF0)分布如图9和图10所示。当B/L=1.2时,左立面平均风压IF0值和极值风压IF0值最大分别为1.01和0.73,整体表现为减小效应,出现这种现象的原因可能是由于切角的存在,增强了流体再附性,流体再附导致立面受到的风压力变大,进而减弱了立面的负风压(表现为风吸力),最终表现出减小效应。当B/L=1.5时,由于间距比的增加,流场干扰能力下降,切角的流体再附效果减弱,干扰效应呈明显的放大效应,此时平均风压IF0取最大值为3.31,极值风压IF0最大值为2.39。当1.5≤B/L<6.0时,平均风压IF0值呈现明显的规律分布,从立面迎风侧(立面右侧)到背风侧(立面左侧),干扰因子逐渐减小,极值风压IF0值规律与平均风压IF0值规律相似,各间距比下IF0最大值均位于立面迎风侧。当6.0≤B/L≤8.0时,平均风压IF0值与极值风压IF0值缓慢减小,当B/L=8.0时,两切角方柱相邻立面仍然存在28%的放大干扰效应。

图9 左立面平均风压系数干扰因子Fig.9 IF0 contours for average wind pressure coefficients

图10 左立面极值风压系数干扰因子分布Fig.10 IF0 contours for extreme wind pressure coefficients
3.3.2 右立面、迎风面和背风面
对于方柱的其他立面,采用块干扰因子(BIF0)描述立面不同区域的干扰大小,图11给出了3个立面不同间距下块干扰因子的分布情况。当B/L=1.2时,迎风面BIF0值分块变化,左侧编号为1、4、7的区域表现为放大效应,位于1号区域,放大效应最大为45%,右侧3、6区域与背风面和右立面均表现为减小效应,其中右立面BIF0值最小,仅为0.74。当B/L=1.5时,3个立面的干扰效应均达到峰值,其中迎风面与背风面靠近左立面(相邻立面)的一侧BIF0值最大,均达到2.00以上。当B/L≥2.5时,各区域BIF0值变化幅度较小,并逐渐趋近于1。


图11 各立面块干扰因子分布Fig.11 BIF0 contours of windward facade, leeward facade
3.3.3 切角
基于方柱各立面的干扰结果,相邻立面与迎风面和背风面的相临侧干扰效应更明显,因此对位于两方柱相邻侧上的切角C和切角D的干扰效应进行研究,图12为两切角的极值风压IF0值随高度(标高见图4)的分布结果。当B/L=1.2时,2个切角表现为明显的减小效应,切角D干扰因子为负,与单体切角方柱相比,此处由风吸力转变为风压力,这是由于2个方柱距离过近,风在进入峡谷(两方柱间的缝隙)时相互作用,产生风压力,改变了切角处的受力情况。这也解释了迎风面相邻侧的放大效应产生原因。当B/L=1.5时,前流场处的切角D仍然表现减小效应,但干扰因子由负变正,说明此时两方柱的相互作用减弱,相互作用产生的风压力并不足以抵消风吸力,因此表现为正值减小效应,随着后续距离的增加,这种相互作用逐渐消失。后流场切角C表现为明显的放大效应,干扰因子最大值为2.58,出现在切角顶部区域。当B/L≥4.0时,干扰因子随间距的增大不再变化,切角处的干扰逐渐消失。

图12 不同标高下切角干扰因子分布Fig.12 IF0 on chamfered corners at different elevations
4 结论
1) 并列方柱的气动干扰效应对切角的变化很敏感。与标准方柱相比,切角方柱的气动力系数有显著减小。当1.5≤B/L<2.5时,两方柱的平均阻力系数呈放大效应,脉动升力系数呈减小效应。当2.5≤B/L≤8.0时,两方柱的平均阻力系数与单体值偏离幅度不超过2%,脉动升力系数先减小后增大,B/L=4.0时取最小值为0.22。
2) 切角会改变小间距并列方柱的风压干扰效应。当B/L=1.2时,由于风在峡谷入口壁面处相互作用,产生了风压力,风压力与建筑各立面和切角受力叠加,迎风面相邻侧正压叠加表现为放大效应,其余立面与切角均为减小效应,其中切角D干扰因子为负值,表现为风压力。由于本文在切角处的测点布置不够多,所以切角处风压变化情况以及变化机理仍然有待进一步试验研究。
3) 切角产生的干扰效应在相邻壁面影响更广,当B/L=1.5时,受扰方柱的干扰因子取得最大值2.58,位于相邻侧后流场的切角C上。当B/L≥4.0时,除左立面外的其他立面与切角的干扰效应趋于消失,左立面仍然存在较大的干扰效应。当B/L=8.0时,两方柱相邻立面仍然存在28%的干扰效应。
