从三角形到多边形的合理迁移和思维培养

窦林

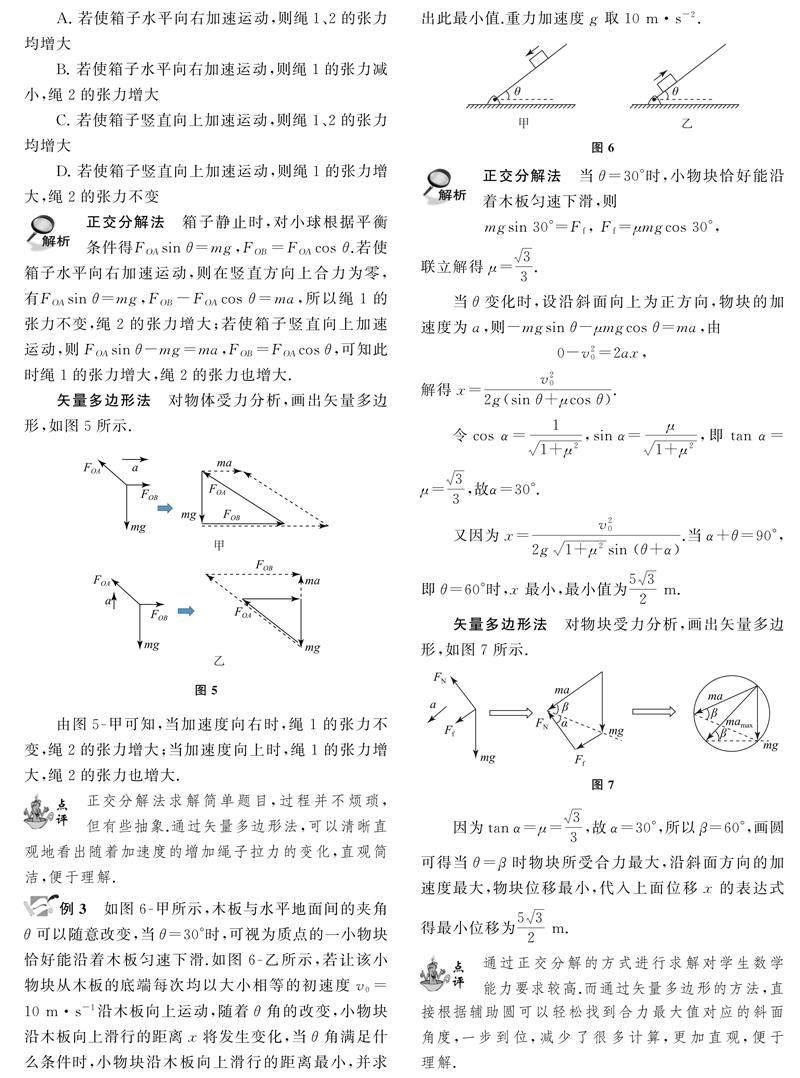
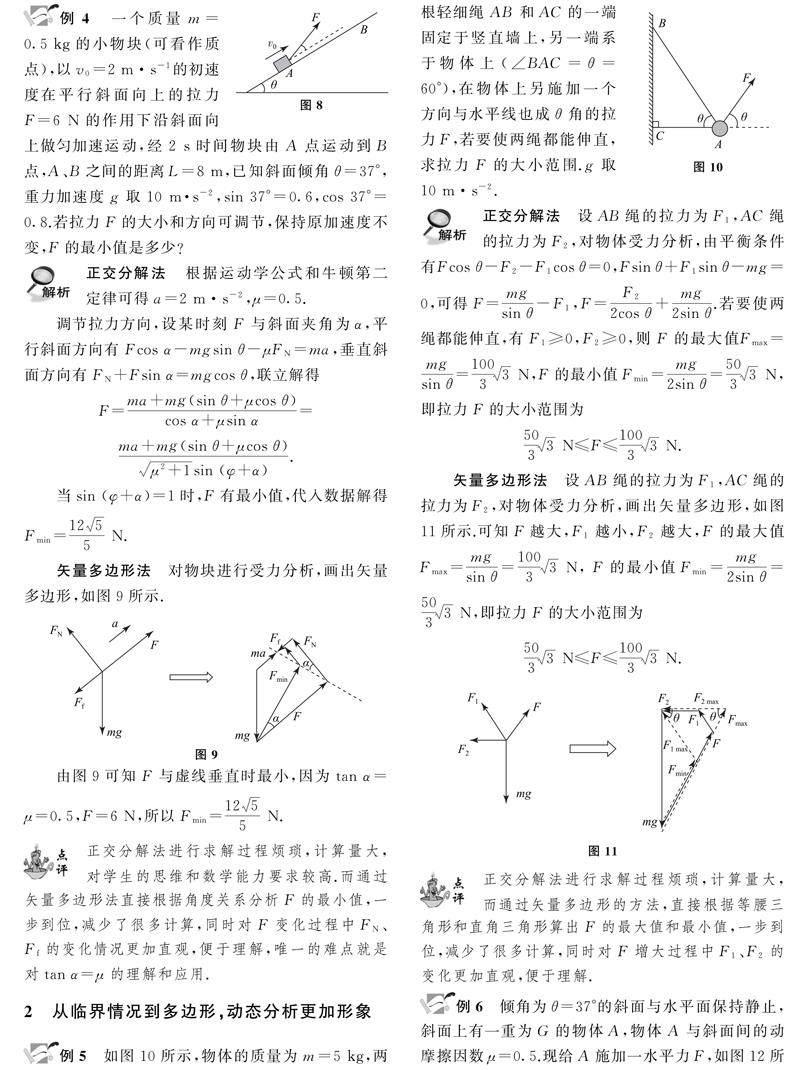
大部分学生在解决力和运动问题时会感觉很难，对于受力分析，要么不会做，要么做不对．产生这种现象的原因是根据传统的正交分解的方法解题时比较抽象，往往計算量很大，对学生计算能力要求较高，学生很容易算错．想要解决上面的问题，笔者认为要教会学生透过问题的表象，挖掘知识的本质．力的合成的本质是矢量加减，在学生完成数学中向量知识的学习后，可以通过画矢量图的方式解决力的合成问题，其中三角形是矢量加法中最简单的模型，而矢量多边形是它的衍生物．相比于矢量多边形，正交分解看似简单，实则计算复杂，是将思维量变成了计算量．利用矢量多边形解决力学问题更加形象简单，计算量小．下面笔者通过几道例题详细解释矢量多边形在解题过程中的应用和优势．