三元锂电池循环寿命的加速试验验证
2024-05-07钱凯程高怡晨
钱凯程 谢 欢 高怡晨 沈 驰
上海机动车检测认证技术研究中心有限公司
0 概述
三元锂电池作为车用锂离子电池的重要技术路线之一[1-3],其发展较为迅速。数据显示,2022年1-12月,我国三元锂电池累计装车量110.4 GWh,占总装车量37.5%,累计同比增长48.6%;2023 年1-5 月,我国三元锂电池累计装车量37.9 GWh,占总装车量31.8%,累计同比增长11.4%。而随着三元锂电池的发展,其寿命不断增长,导致电池正常寿命测试的时间和经济成本不断加大。因此,研究选取加速因子,通过提高测试三元锂电池的敏感应力水平加快失效模式的发生,建立加速因子试验寿命与正常工况下寿命的联系,显得愈发重要。常见的加速因子有:温度、循环倍率、充放电截止水平等[4-7]。
茆诗松研究了几种常用的加速模型,如阿伦尼斯(Arrhenius)模型、逆幂律模型、单应力的艾林(Egring)模型、广义艾林模型等,并解释了模型的主要参数及应用维度等[8]。吴欢欢等基于Arrhenius公式,分别构建了电池的倍率及温度加速模型,该模型在一定加速应力范围内,可快速预测电池循环寿命,缩短测试时间[9]。黄海宁通过测试磷酸铁锂电池在不同温度下的循环衰减曲线,研究其衰减特点,得到电池存在最优循环温度区间,运用dV/dQ-Q 曲线分解衰减来源,并运用温度加速对电芯循环寿命衰减进行寿命拟合和寿命预测,在特定的温度区间内具有较好的预测准确性[10]。丁鹏飞等基于逆幂律模型,研究了三元锂电池在不同放电倍率下以循环寿命衰减拟合的二次多项式系数为寿命特征的加速寿命模型[11]。王芳等结合电池衰退模型建立了寿命加速预测方法,根据电池在不同温度下的衰减速度,得出电池寿命随温度衰减模型,从而实现了通过检测高温下日历寿命推算电池的实际日历寿命[12]。邓爽等通过容量衰减数据推导其循环寿命衰减内在的联系,使用二项式拟合,构建Arrhenius 数学模型获得不同温度下电池容量衰减规律,提出了一种电池容量衰减的加速预测方法[13]。STROE等设计了两个测试矩阵,同时开展了加速日历和循环老化试验,由此建立了预测模型,并将预测结果与新电池试验结果进行对比,验证效果良好[14]。李广地等对国内外动力锂电池的寿命研究进行了综述,从动力电池的寿命定义入手分析了温度、充放电电流、充放电截止电压等因素对电池寿命的影响[15]。
本文以温度作为加速因子,通过机器学习中的岭回归方法研究确定合适的拟合方程,最后基于阿伦尼斯模型,建立不同寿命特征的加速寿命模型预测并进行验证,为三元锂电池在寿命预测方面的研究提供参考。
1 试验对象与试验方法
本文选用的三元锂电池,其充/放电截止电压为4.25 V/2.8 V。加速因子方面,选取25、45、55 ℃作为不同的温度输入,研究三元锂电池的加速寿命特征。循环倍率、充放电截止水平作为动力电池寿命的主要影响因素,若同时进行试验分析将影响试验设计与试验结果分析,故在本文中固定循环倍率为1 C 充-1 C 放、充放电截止水平为14%~97%SOC。另外,本次试验标准容量标定法如下:
1)环境箱设置25 ℃,电池恒温至25±2 ℃;
2)电池以1 C 恒流-恒压(CC-CV)充电至4.25 V,截止电流0.05 C,静置0.5 h;
3)电池以1 C恒流放电至2.8 V,静置0.5 h;
2)-3)步循环三次,并以第三次循环的放电容量作为标准容量。
将三元锂电池置于环境箱中,不同温度下循环寿命试验具体流程为:
1)标准容量标定1次,得到初始标准容量;
2)环境箱设置25 ℃(45 ℃/55 ℃),电池恒温至25±2 ℃(45±2 ℃/55±2 ℃);
3)1 C 恒流-恒压(CC-CV)充电至97%SOC,截止电流0.05 C,静置0.5 h;
4)1 C恒流放电至14%SOC,静置0.5 h;
5)循环3)~4)100次;
6)标准容量法标定1次;
7)返回第2)步,直至标准容量测得容量下降至初始容量的80%以下,则认为电池寿命终止。具体试验流程图见图1。
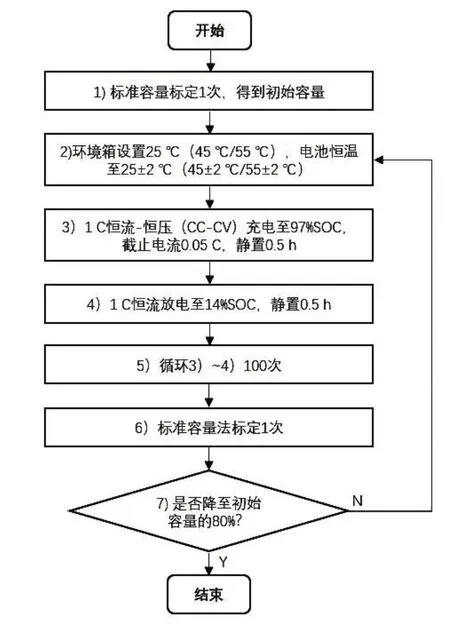
图1 不同温度下循环寿命试验
1.1 岭回归拟合数据样本
岭回归(Ridge Regression)属于机器学习中的有监督学习一类,可以用来对数据样本进行拟合及预测,其采用了L2 正则化,可以防止过拟合。岭回归目标函数[Jθ]的表达方式可以写为:
式(1)中:θ——拟合方程系数;
X——输入值;
y——真实值;
α——调整参数。
由此可以发现,影响拟合效果主要取决于两方面:拟合方程的选定、[α]大小的选定。
1.2 确定拟合方程的形式
首先确定拟合方程的形式。根据循环寿命数据的规律,判断拟合方程可能为三次多项式、二次多项式、一次多项式,则有统一拟合方程形式为:
式(2)中:——容量保持率;
x——循环次数;
a、b、c、d——分别为三次项系数、二次项系数、一次项系数及截距。
以25 ℃下循环寿命测试数据为例,在岭回归算法应用过程中,将数据集分为训练集和验证集(8∶2),先固定α值为1,分别拟合出三次多项式方程(degree=3)、二次多项式方程(degree=2)、一次多项式方程(degree=1),得到图2。相应地,对于45 ℃下循环寿命测试数据、55 ℃下循环寿命测试数据拟合得到图3、图4。

图2 25 ℃下循环寿命数据拟合
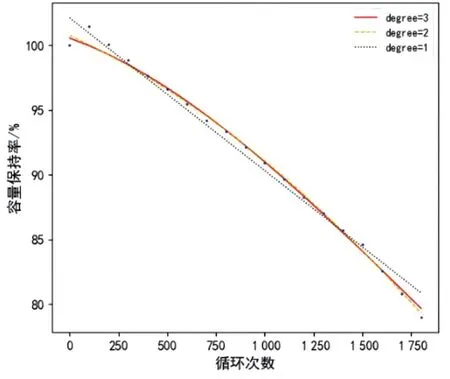
图3 45 ℃下循环寿命数据拟合

图4 55 ℃下循环寿命数据拟合
进一步可以对三次多项式方程、二次多项式方程、一次多项式方程的拟合效果进行评价。以25 ℃下循环寿命测试数据为例,不同多项式方程对应的系数及效果见表1。由表1可见,在验证集中,二次多项式的R-square 最高,达到了0.99 以上。根据验证集效果等综合确定选取二次多项式来拟合本文试验所得数据。

表1 25 ℃下循环寿命数据不同多项式方程拟合系数及效果
1.3 确定正则化力度
其次确定α正则化力度。对于α的选择,可以通过“各回归系数的岭估计基本稳定”这一原则确定。仍以25 ℃下循环寿命测试数据为例,从图5、图6 可以看到,岭迹线(回归系数和α值之间的关系)在α取值范围10^-2至10^2的这一段区间基本稳定,因此α合适值可以取1。
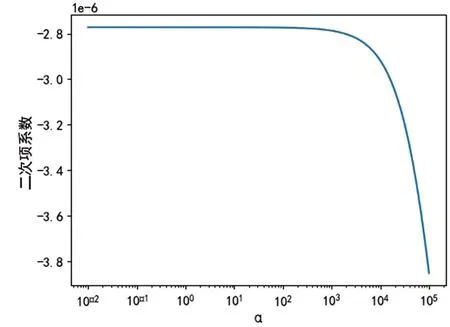
图5 一次项系数岭迹线

图6 二次项系数岭迹线
综上确定拟合方程采用二次多项式形式,α取1,则最终25 ℃下循环寿命测试数据、45 ℃下循环寿命测试数据、55 ℃下循环寿命测试数据,用岭回归方法拟合得到的系数及效果见表2。各二次项方程为:

表2 不同温度下循环寿命数据二次多项式方程拟合系数及效果
2 以500次循环、1 000次循环容量保持率为寿命特征建立加速寿命模型
温度作为加速应力在加速寿命试验中是较为常见的,高温能使材料内部的化学反应加快,从而引发提前失效。阿伦尼斯研究了这类化学反应,并在大量数据的基础上,提出了如下模型:
式中:ξ——寿命特征;
A——个正常数;
E——激活能,与材料有关;
K——玻尔兹曼常数;
T——绝对温度。
采用对数方法将其线性化可以得到:
式(7)中:a=lnA,b=E/K,表明寿命特征的对数是温度倒数的线性函数。
基于阿伦尼斯模型,分别取25 ℃/55 ℃下500次循环容量保持率、25 ℃/55 ℃下1 000 次循环容量保持率作为寿命特征,进行加速寿命模型建立和误差分析。见表3,当500 次循环时,25 ℃下容量保持率为96.59%、55 ℃下容量保持率为91.20%;当1 000 次循环时,容量保持率分别为90.93%、81.11%。
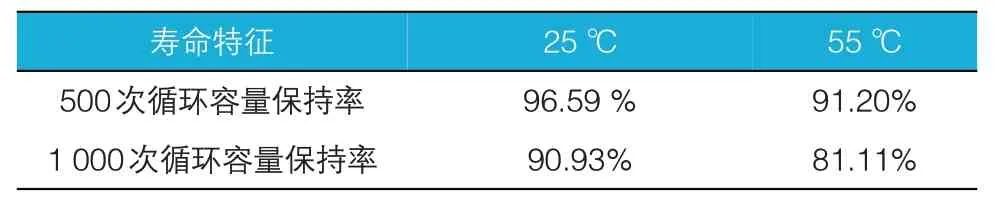
表3 不同温度下循环500次循环容量保持率、1 000次循环容量保持率
以500 次循环容量保持率、1 000 次循环容量保持率为寿命特征构建得到的加速寿命模型分别为:
式(8)、式(9)中:ξ分别指500次循环容量保持率、1 000次循环容量保持率。对应图7、图8。
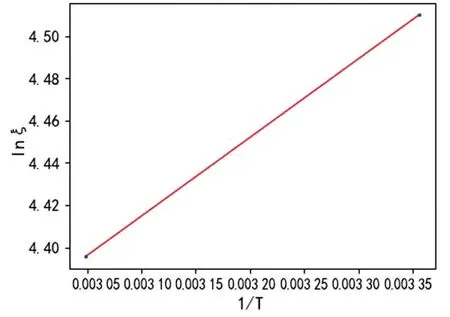
图7 以500次循环容量保持率为寿命特征
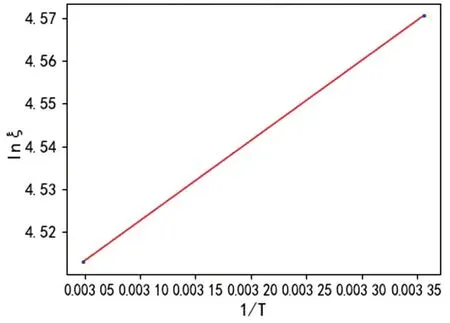
图8 以1 000次循环容量保持率为寿命特征
使用上述由25 ℃数据与55 ℃数据构建得到的两个加速寿命模型分别验证45 ℃下500次循环、1 000次循环时的容量保持率,见表4。
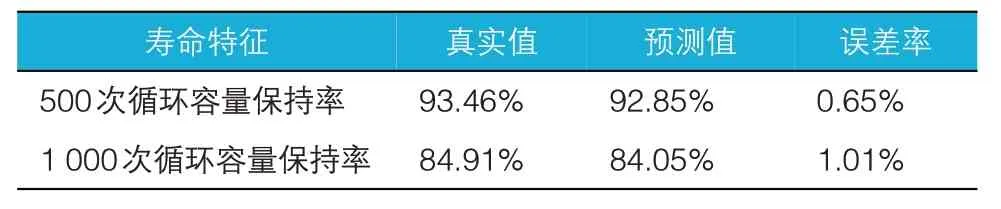
表4 45 ℃下循环时两种寿命特征加速模型误差
由表4 可见,该加速寿命模型预测的结果准确度较高,类似地,也可以用同样的方法预测其它循环次数对应的容量保持率,但是,这样的方法不能预测电池循环容量衰减的整个曲线过程。因此考虑将前文推导得到的多项式系数作为寿命特征,由此可以构建出整个曲线过程的加速寿命模型,进而可以预测任一点寿命。
3 以多项式系数作为寿命特征建立加速寿命模型
观察式(3)、式(4)、式(5),其二次项系数之间和一次项系数之间呈规律分布,因此,分别取二次项系数的绝对值和一次项系数的绝对值为寿命特征,基于25 ℃下循环寿命测试数据、55 ℃下循环寿命测试数据建立不同充电倍率循环之间的联系,得到:
式(10)、式(11)中:ξ分别指一次项系数绝对值、二次项系数绝对值。对应图9、图10。
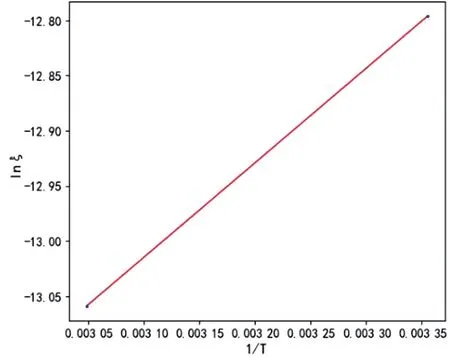
图9 一次项系数绝对值为寿命特征

图10 二次项系数绝对值为寿命特征
由此,加速寿命模型的一次项系数、二次项系数得以确定,注意最后要取负。再观察式(3)、式(5),得到加速寿命模型的常数项可取式(3)、式(5)常数项的均值,因此,最终得到的加速寿命模型为:
图11为45 ℃下循环试验所得的容量保持率散点图(蓝色)与采用上述模型预测的容量保持率(红色)对比,可以看到拟合效果较好,使用多项式系数作为寿命特征构建得到的加速寿命模型准确度较高,具有一定的参考意义。
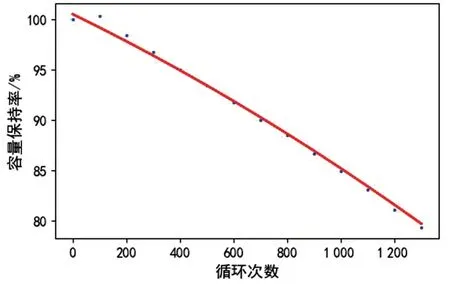
图11 45 ℃下循环预测结果与试验结果对比
分别选取300 次循环、600 次循环、900 次循环、1 200 次循环时预测容量保持率,与试验所得容量保持率进行对比,发现误差率都在1%以下,见表5。

表5 45 ℃下循环时以多项式系数构建的加速寿命模型误差
4 总结
本文基于不同温度下的三元锂电池循环寿命试验,结合机器学习中的一些思想及方法,应用阿伦尼斯模型,得到了以下结果:
1)应用机器学习中的岭回归方法对获得的数据进行三次多项式、二次多项式、一次多项式及不同正则化力度的拟合,从而确定最合适于当前循环寿命容量衰减数据的拟合方程形式,该方法具备一定的泛化应用意义;
2)基于阿伦尼斯模型,建立了以电池500 次循环、1 000 次循环对应容量保持率为寿命特征的加速寿命模型预测单点寿命,建立了以二次多项式系数为寿命特征的加速循环寿命模型预测曲线任一点寿命,经与试验结果对比发现预测精度较高,可以在适当范围内用于电池容量衰减的加速测试与评估,为控制策略制定提供帮助。
