泵控液压系统中马达转速稳定控制及仿真分析

韩钰，邹炳燕

(天津中德应用技术大学基础实验实训中心，天津 300350)

0 前言

泵控液压马达系统由于避免了节流损失，效率较高[1-3]，因此在移动装备中应用广泛[4-6]。在泵控液压马达系统中，时常需要维持液压马达转速稳定的工况。但当变量泵的转速主动发生变化，或由于负载的影响而导致变量泵转速被动发生变化时，都会显著增加马达在恢复目标转速之前的调整时间和增大马达转速的波动量。当变量泵转速主动发生变化时，国内相关学者对稳定马达转速的工况做了相关研究。柴小波等[7]对定量泵-变量马达系统进行分析，提出了以系统流量为中间控制变量的方法，对变量马达摆角进行补偿控制来稳定马达转速；郭初生等[8]针对泵控马达系统中变量泵的转速变化，综合扰动乘积补偿方法和PI控制方法实现马达转速控制；李昊、杨玉强[9]以车载液压发电系统为研究对象，针对行车过程中发动机转速主动实时变化对系统的影响，采用发动机转速信号为前馈补偿信号来稳定马达转速；王春光、杨玉强[10]针对泵控马达系统在变量泵变转速输入下，加入转速补偿控制和积分分离PID控制实现马达转速的稳定输出。以上文献主要研究了变量泵转速主动发生变化的情况，而针对变量泵转速受负载影响而被动变化时，稳定马达转速的相关研究比较少。针对此情况，本文作者提出一种前馈补偿方式来抑制马达转速波动，减少马达的调整时间。

1 马达转速波动的分析

泵控液压马达系统原理如图1所示。发动机驱动变量泵1，变量泵1驱动定量液压马达2，液压马达2驱动负载。当外负载突然变化时，高压管路的工作压力骤然变化，进而引起驱动变量泵的扭矩也随之改变。又因发动机与变量泵直接相连，扭矩的改变导致发动机转速产生变化，发动机转速的变化又传给变量泵，最终导致液压马达的转速产生波动。在这一系列变化过程中，变量泵转速的被动变化会显著增加液压马达恢复目标转速之前的调整时间及增大马达转速的波动量。

图1 液压原理

2 泵控液压系统数学模型

2.1 比例放大器数学模型

比例放大器的作用是将电压偏差信号转化为电流信号。由于其响应频率远大于泵控马达系统频率，故可将其视为比例环节。输入电压U与输出电流I的传递函数为

Ka=I(s)/U(s)

(1)

式中：Ka为比例放大器增益。

2.2 电流-电比例阀阀芯位移数学模型

比例放大器输出的电流信号需要驱动变量泵控制机构的电比例阀，由于电比例阀的固有频率远大于泵控马达系统频率，故可将其视为比例环节。输入电流I与阀芯输出位移Xv的传递函数为

Kvi=Xv(s)/I(s)

(2)

式中：Kvi为比例增益。

2.3 阀控变量缸数学模型

电比例阀的阀芯Xv移动微小距离后，液压油经电比例阀进入变量液压缸，驱动变量缸移动，变量缸的活塞杆一端与变量泵的斜盘连接，改变斜盘角度。同时，变量缸的活塞杆另一端与电比例阀的机械反馈杆连接，进行闭环反馈，保证活塞杆位移Xp准确输出。

在不考虑机械反馈的情况下，阀芯Xv与活塞杆位移Xp的传递函数可描述为

(3)

式中：ωh为阀控缸液压固有频率；ξh为阀控缸液压阻尼比；Kq为流量增益，A为变量缸有效作用面积。

考虑存在机械反馈，设反馈系数为Kf，结合式(3)，可得闭环传递函数为

(4)

2.4 变量泵斜盘-变量缸活塞位移数学模型

变量泵斜盘与变量缸活塞杆铰接在一起，分析其结构可得，斜盘摆角γ与活塞杆位移xp的传递函数为

1/L=γ(s)/xp(s)

(5)

式中：L为油缸施力点到斜盘铰点间的距离。

2.5 变量泵输出流量的数学模型

变量泵输出流量的微分方程为

Qp=KPωPγ-Cip(p1-pr)-Cepp1

(6)

式中：Qp为高压管路流量；KP为变量泵的排量梯度；ωP为变量泵的转速；Cip为变量泵的内泄漏系数；Cep为变量泵的外泄漏系数；p1为高压侧管路压力；pr为低压侧管路压力。

若假定变量泵转速ωP恒定，系统回油管路压力pr恒定，则其增量方程的拉氏变换为

QP(s)=KPωPγ(s)-CtpP1(s)

(7)

其中：Ctp为变量泵的总泄漏系数，Ctp=Cip+Cep。

2.6 液压马达高压腔流量的数学模型

液压马达高压侧流量连续微分方程为

(8)

式中：Cim为液压马达的内泄漏系数；Cem为液压马达的外泄漏系数；Dm为液压马达排量；θm为液压马达的转角；V0为高压侧管路总体积；βe为油液有效体积弹性模量。

其增量方程的拉氏变换为

QP(s)=CtmP1(s)+Dmsθm(s)+(V0/βe)sP1(s)

(9)

式中：Ctm为变量泵的总泄漏系数，Ctm=Cim+Cem。

2.7 液压马达和负载力矩的数学模型

液压马达和负载力矩平衡的微分方程为

(10)

式中：Jt为马达和负载的总惯量；TL为作用在马达上的负载力矩；Bm为黏性阻尼系数。

其增量方程的拉氏变换为

DmP1(s)=Jts2θm(s)+Bmsθm(s)+TL(s)

(11)

2.8 转速传感器的数学模型

转速传感器将马达的转速信号反馈到控制器中，通过与目标值做减法得到偏差信号进行反馈控制。由于转速传感器的响应很快，其固有频率远大于泵控系统的固有频率，因此可将其简化为比例环节，其传递函数为

(12)

式中：Kv为转速传感器增益。

2.9 泵控液压系统的传递函数框图

在式(7)的推导过程中，假定了变量泵的转速ωP是恒定的，但实际情况下变量泵的转速是变化的，与发动机转速一致。当发动机的扭矩变化而导致发动机的转速变化时，泵的转速也会随之变化。因此在画系统框图的时候，要将发动机单独做成一个模型，再与变量泵排量Dm做成乘积的形式。综合式(1)(2)(4)(5)(7)(9)(11)(12)可得传递函数框图如图2所示。

图2 补偿前传递函数框图

图中：Tω为给发动机的扭矩反馈；Ct为系统总泄漏系数，Ct=Ctm+Ctp。

3 稳定马达转速的前馈补偿控制

当发动机转速受到马达外负载影响而改变时，进一步加剧了马达转速的波动。除了系统的闭环反馈稳定马达转速外，文中还加入了前馈补偿控制方式补偿发动机转速波动对系统的影响，实现马达转速的稳定控制。

在分析变量泵转速ωP的扰动时，式(6)中的KPωPγ有2个自变量，分别是ωP和变量泵斜盘摆角γ，2个自变量呈非线性关系，因此在做拉氏变换时，需要在平衡点附近展开成泰勒级数进行线性化处理[11]。平衡点选取为零负载且马达转速稳定时的点。将式(6)泰勒级数展开如下：

QP(s)=KPωPγ(s)+KPω0Δγ+KPγ0ΔωP+KPΔωPΔγ-CtpP1(s)

(13)

式中：ω0为平衡点处泵的转速；Δγ为泵斜盘摆角的扰动量；γ0为平衡点处斜盘的摆角；ΔωP为泵转速的扰动量。忽略无穷小量KPΔωPΔγ及KPω0Δγ(工程上Δγ不易测量)，再与式(7)比较，可知只差KPγ0ΔωP这一项，该项即为变量泵转速扰动引起的流量变化。

根据结构不变性原理[12-16]，引入补偿函数GT(s)，以转速扰动量ΔωP为输入，对KPγ0ΔωP这一项的流量进行补偿，如图3所示，推导可得：

(14)

图3 补偿后传递函数框图

将GB的具体表达式代入式(14)，可得：

(15)

式(15)中有三阶微分环节，工程上难以实现，考虑到阀控变量缸震荡环节固有频率很高，可以忽略[8]，故式(15)可化简为

(16)

式中：γ0可根据平衡点处以及马达转速稳定时，变量泵的输入流量与马达所需流量相等而计算求得。

4 仿真验证

根据图3并结合相关文献的发动机模型[17]，建立系统仿真模型，如图4所示。

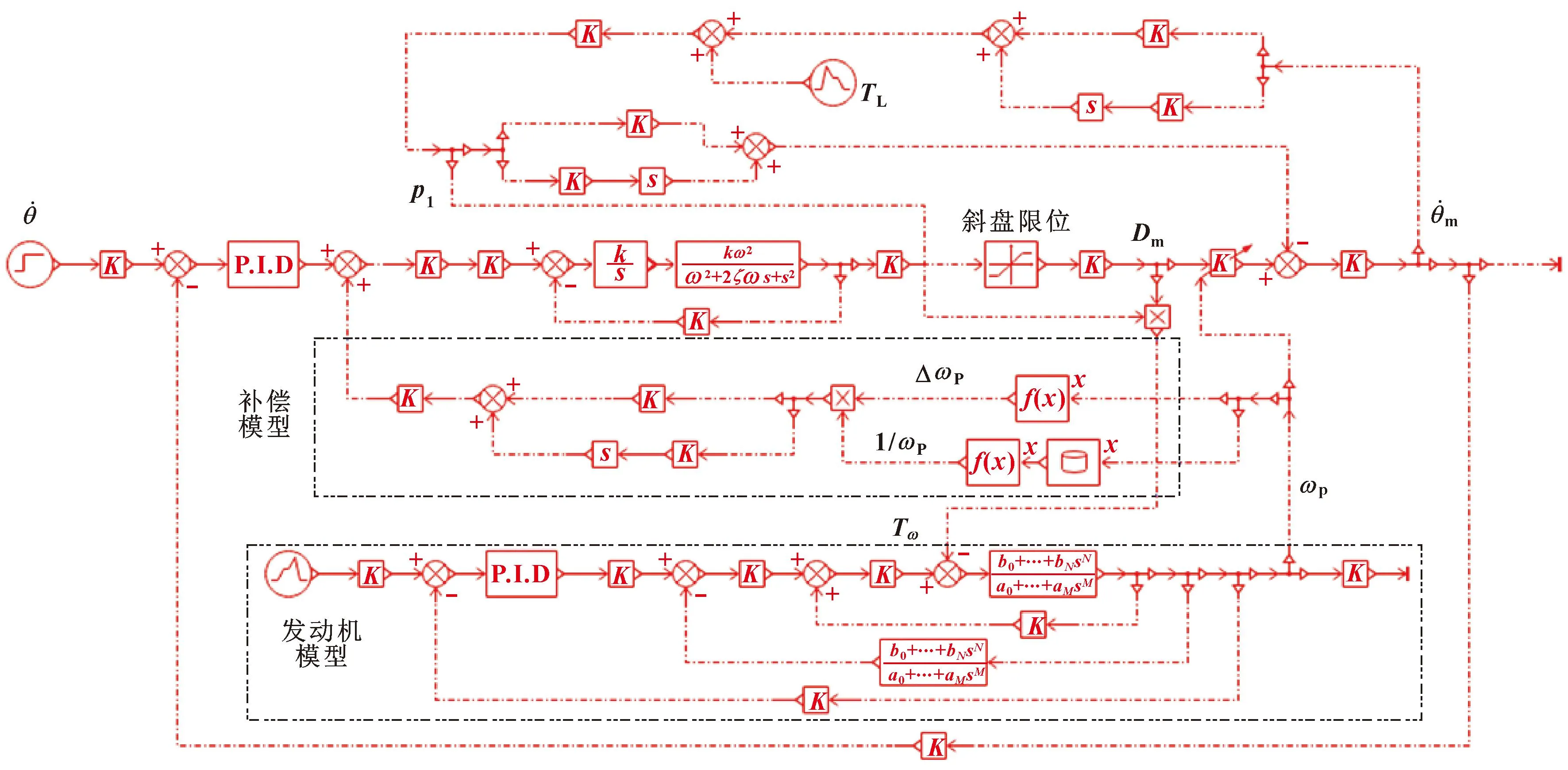
图4 系统仿真模型

选取某车载液压发电系统的一组数据进行仿真。仿真主要参数见表1。

表1 仿真模型主要参数

为了验证仿真模型的正确性，在30 s突加12 kW(100%)载荷，针对马达输出转速做了仿真曲线和实验曲线的对比，如图5所示。可知：马达转速在34 s左右趋于稳定值1 500 r/min，仿真结果与实验结果基本相符，建立的仿真模型符合实际工况。

图5 仿真与实验的比较

4.1 阶跃满载(100%)工况下马达转速分析

发动机输出转速如图6所示。在0 s时，给定发动机转速信号为1 200 r/min，经过发动机自身的转速反馈，在9.5 s后，发动机实际输出转速最终稳定在目标转速1 200 r/min。在30 s时，由于马达外负载扭矩突然增加，导致发动机转速立即下降并产生转速波动；且无前馈补偿时，发动机最低转速为1 021 r/min；有前馈补偿时，发动机最低转速为990 r/min。有前馈补偿时发动机最低转速更低的原因是补偿环节调节了变量泵的排量使其增加，进而导致驱动变量泵的发动机扭矩增加得更多，因此发动机转速下降也更为严重。在60 s时，由于马达外负载扭矩突然减小，导致发动机转速上升，且无前馈补偿时，发动机最高转速为1 370 r/min；有前馈补偿时，发动机最高转速为1 381 r/min。此外，发动机转速不受负载扭矩影响时，转速基本恒定在1 200 r/min。

图6 发动机输出转速

由图7可知：液压马达空载工作且转速稳定后，30 s时突加阶跃负载TL(100%)，可以看到有前馈补偿及无前馈补偿的马达转速都骤然减小，虽然最大波动量几乎相等，约为11.5%，但有前馈补偿措施的马达转速多在目标转速1 500 r/min附近波动，且其调整时间为0.62 s；无前馈补偿的调整时间为2.15 s。当变量泵转速恒定时，有前馈补偿的曲线与恒速曲线基本相符但没有完全重合，这是因为补偿模型中忽略了式(13)中的KPΔωPΔγ、KPω0Δγ。但在大部分工程应用中，其精度是满足要求的。

图7 阶跃突加满载(100%)工况下马达转速

由图8可知：在马达满载且液压马达转速稳定后，60 s时突减阶跃负载TL(100%)，可以看到有前馈补偿及无前馈补偿的马达转速都骤然增大，虽然转速最大波动量基本相同，约为11.4%，但有前馈补偿的马达转速多在1 500 r/min附近波动，且有前馈补偿的调整时间为0.56 s；无前馈补偿的调整时间为1.92 s。

图8 阶跃突减满载(100%)工况下马达转速

4.2 阶跃20%负载工况下马达转速分析

由图9可知：液压马达空载工作且转速稳定后，30 s时突加阶跃负载TL(20%)，可以看到马达转速最大波动量比满载时要小很多，但最大波动量基本相同，约为2.33%，但有前馈补偿的马达转速多在1 500 r/min附近波动，其调整时间为0.13 s；无前馈补偿的调整时间为0.14 s，调整时间相差很小。

图9 阶跃突加负载(20%)工况下马达转速

由图10可知：在马达20%负载且液压马达转速稳定后，60 s时突减阶跃负载TL(20%)，可以看到马达转速最大波动量基本相同，约为2.26%，有前馈补偿的调整时间为0.13 s；无前馈补偿的调整时间为0.14 s，调整时间也相差很小。

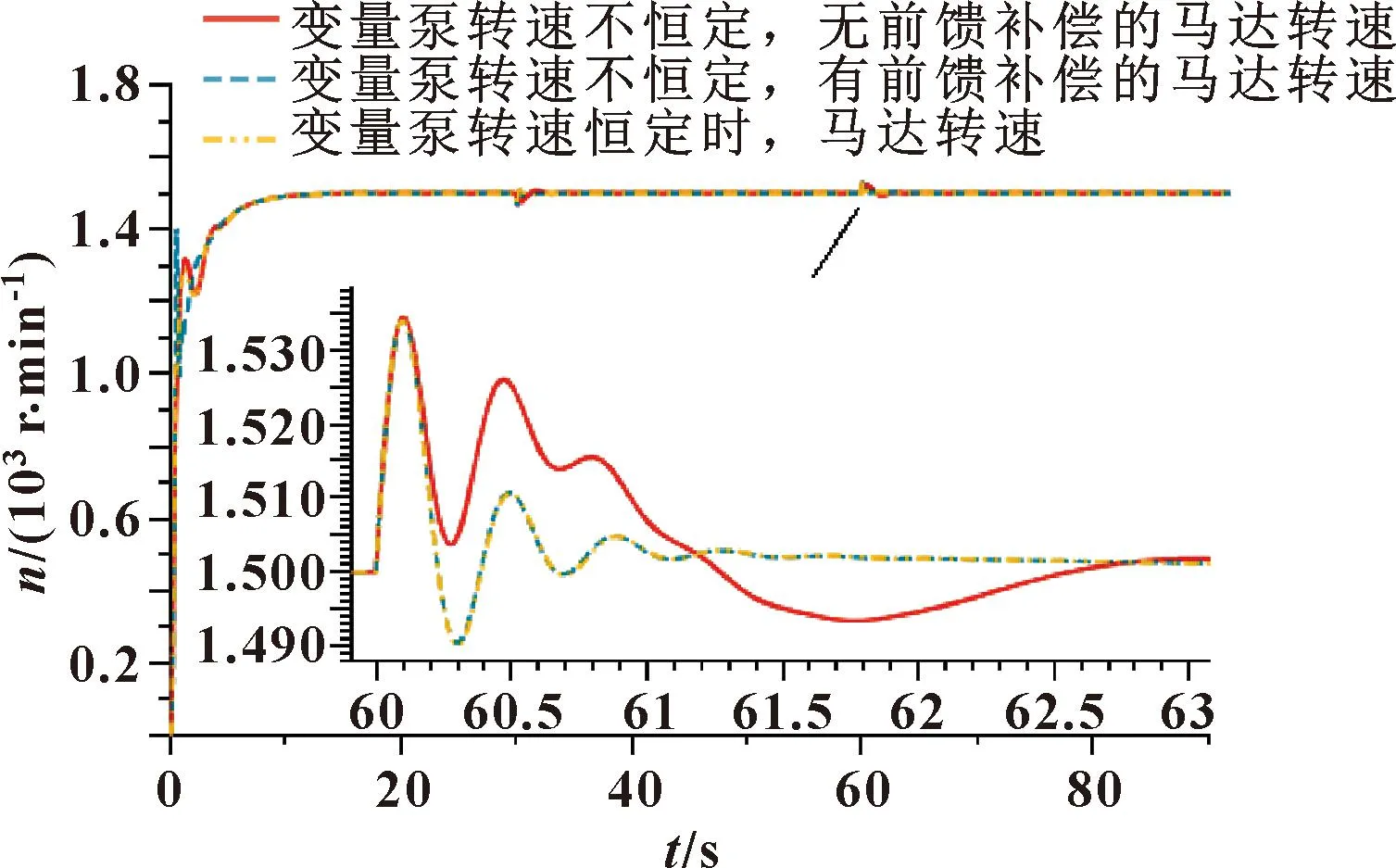
图10 阶跃突减负载(20%)工况下马达转速

4.3 斜坡满载(100%)工况下马达转速分析

由图11可知：液压马达空载工作且转速稳定后，30 s时突加斜坡负载TL(100%)，斜坡时间为0.5 s，可以看到有前馈补偿及无前馈补偿的马达转速都骤然减小，但最大波动量不同。有前馈补偿的马达转速最大波动量为3.46%，其调整时间为0.62 s；无补偿的转速最大波动量为7.33%，调整时间为2.39 s。

图11 斜坡突加满载(100%)工况下马达转速

由图12可知：液压马达满负载工作且转速稳定后，60 s时突减斜坡负载TL(100%)，斜坡时间为0.5 s，可以看到有前馈补偿及无前馈补偿的马达转速都骤然增加，但最大波动量不同。有前馈补偿的马达转速最大波动量为3.20%，其调整时间为0.60 s；无补偿的转速最大波动量为6.46%，调整时间为2.11 s。

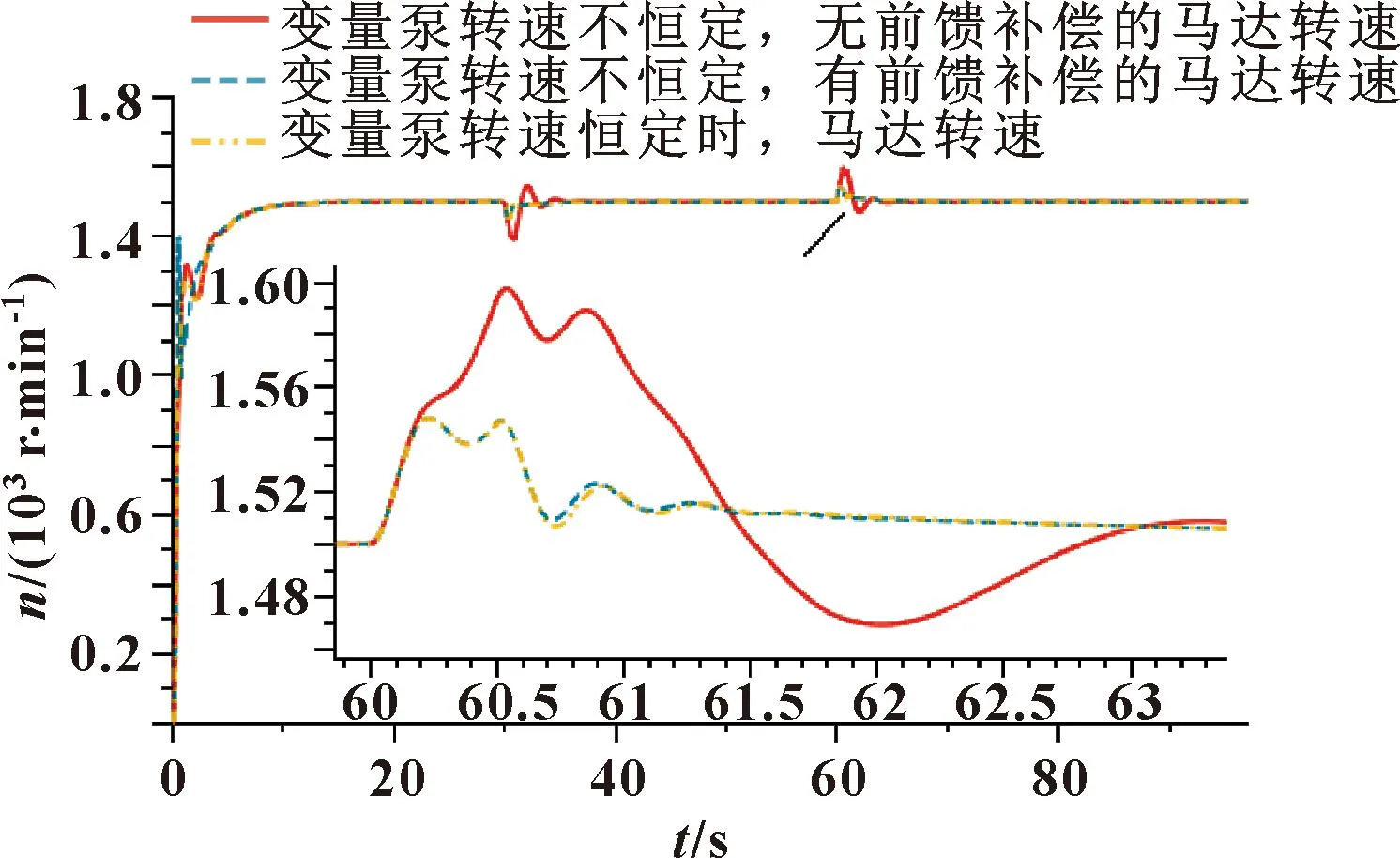
图12 斜坡突减满载(100%)工况下马达转速

4.4 斜坡20%负载工况下马达转速分析

由图13可知：液压马达空载工作且转速稳定后，30 s时突加斜坡负载TL(20%)，斜坡时间为0.5 s。可以看到有前馈补偿的马达转速最大波动量为0.67%，无前馈补偿的转速最大波动量为1.33%。按照2%马达转速波动计算调整时间，转速波动均在2%之内。

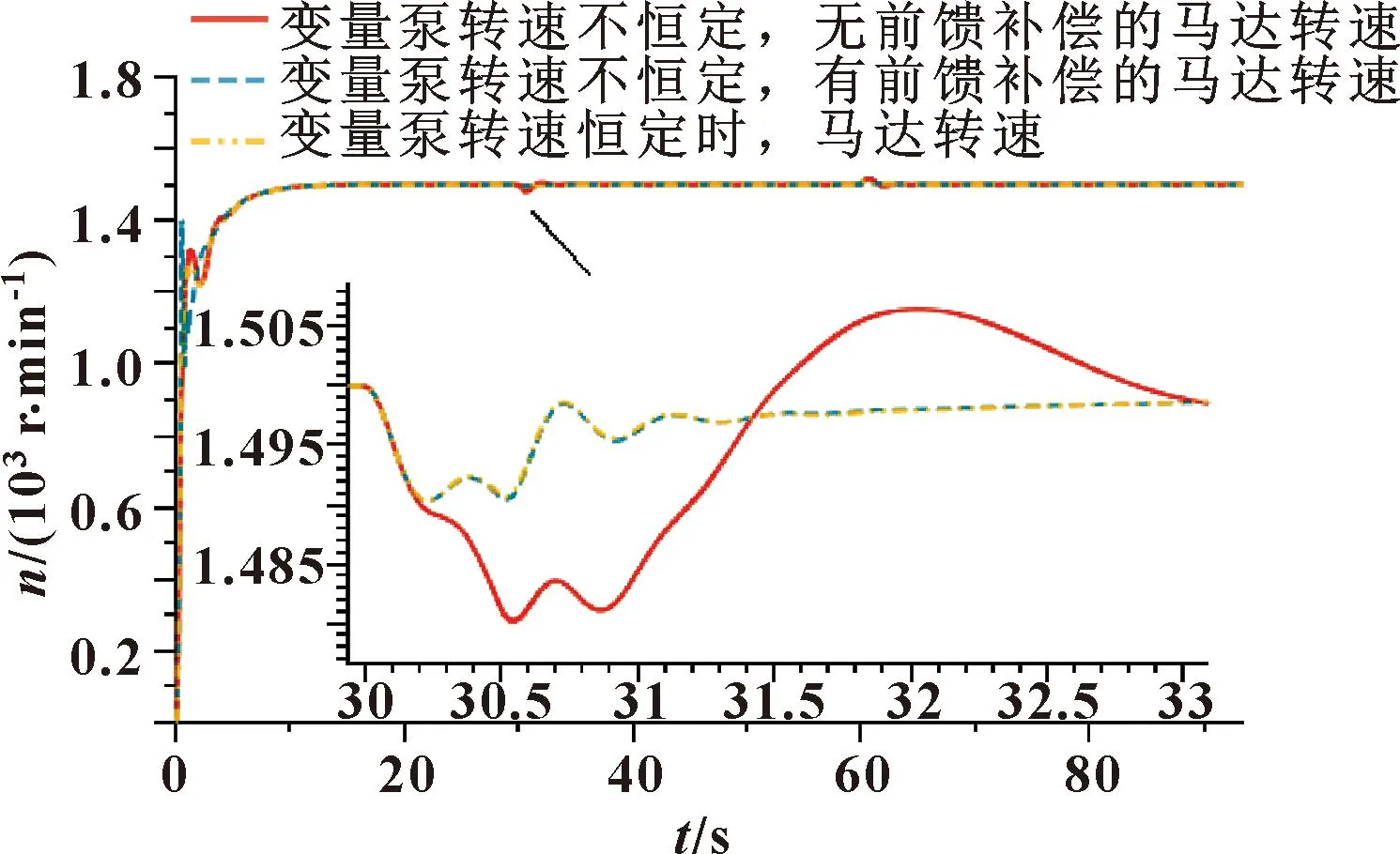
图13 斜坡突加负载(20%)工况下马达转速

由图14可知：液压马达20%负载工作且转速稳定后，60 s时突减斜坡负载TL(20%)，斜坡时间为0.5 s。可以看到有前馈补偿的马达转速最大波动量为0.64%，无前馈补偿的转速最大波动量为1.26%。转速波动均在2%之内。

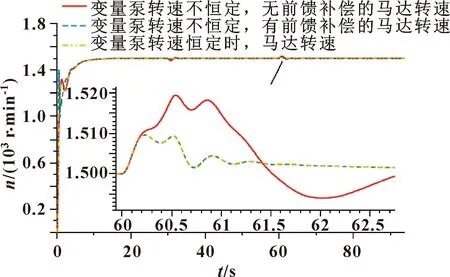
图14 斜坡突减负载(20%)工况下马达转速

5 结论

(1)泵控液压马达系统中，针对负载变化引起变量泵转速被动扰动而导致的马达转速波动问题，提出了一种前馈控制方法，实现了马达输出转速的稳定控制。

(2)在阶跃突加100%负载工况下，通过前馈补偿，调整时间最大缩短了1.53 s。在阶跃20%负载工况下，有前馈补偿的调整时间缩短了0.01 s。在斜坡突加100%负载工况下，通过前馈补偿，马达转速波动量最大减少了3.87%，调整时间缩短了1.77 s；在斜坡突加20%负载工况下，有前馈补偿的马达转速波动减小了0.66%。前馈补偿控制有效抑制了马达转速波动，减小了调整时间。