微型轴向柱塞泵球面配流副预升压区优化设计

刘伟，吴怀超，侯刚，王佩瑾，曹明远，朱彬

(1.贵州大学机械工程学院，贵州贵阳 550025；2.贵阳海之力液压有限公司，贵州贵阳 550018)

0 前言

轴向柱塞泵是依靠柱塞在缸孔中往复运动使得密封容积变化来实现吸油与排油的一类液压泵，由于其压力高、结构紧凑、效率高、流量调节方便，故在需要高压和大流量的系统中应用广泛[1-2]。随着工业技术的不断发展和进步，对轴向柱塞泵的高压、高速、微型化的要求越来越高[3]，尤其是机器人、医疗器械、深海探测、潜艇、航空、航天等领域对液压动力元件的安装空间、外形、质量以及性能指标的限定严格，因此，高速高压微型轴向柱塞泵研究的热度越来越高[4-5]。

高速高压微型轴向柱塞泵配流过程中，预升压过渡区的柱塞对油液进行压缩；三角槽接通低压柱塞腔与高压出口，高压油液倒灌进入柱塞腔，柱塞腔压力快速上升至出口压力。预升压区可以降低压力脉动、流量脉动[6]。不同于中大型柱塞泵，在微型轴向柱塞泵配流过程中，极小的过流面积变化会引起较大的压力脉动，所以若要降低微型轴向柱塞泵的压力脉动，提高配流性能，对预升压区的结构进行优化设计十分必要。单向旋转微型轴向柱塞泵只能按照设计方向旋转，与双向旋转的柱塞泵不同，其三角槽多了一个错配角参数。本文作者建立单向旋转的高速高压微型球面配流副预升压过渡区压力p和过流面积S与三角槽深度角β、宽度角α、开度角φ、错配角φ0以及缸体转角φ的数学模型，并采用粒子群优化算法对预升压区进行结构优化，以改善该类泵的配流性能。将优化结果导入Fluent进行仿真分析，验证优化后的结构降低压力脉动的效果。

1 预升压区瞬时压力数学模型的建立

图1是贵阳某公司研发的单向旋转高速高压微型轴向柱塞泵球面配流副的结构示意。文中研究的微型轴向柱塞泵配流副结构不同于传统的中大型轴向柱塞泵的平面配流结构，而是采用球面配流副。该结构能减小配流副的整体尺寸，受力情况以及力的对中性都优于平面配流结构，为轴向柱塞泵的微型化提供了有力的保障。文中研究的单向旋转微型轴向柱塞泵球面配流副的预升压区和预减压区各开一个三角槽，预升压区三角槽结构剖视图如图1中A-A、B-B所示。图中：ω为缸体转动角速度；R为球面半径；r0为缸体通油孔分布圆半径；β为三角槽深度角；α为三角槽宽度角；Δφ为油液压缩区包角；φ0为错配角。在球面配流盘上建立坐标轴中心位于球面上的空间直角坐标系，如图1所示，预升压区三角槽的结构示意如图2所示。其中：φ为三角槽开口角；φ为缸体转角；定义过流面积S为egf围成的曲面三角形，且平面egf⊥平面adh。

图1 球面配流盘结构示意

图2 三角槽结构示意

由图1所建立的空间直角坐标系可得坐标h(xh,yh,zh)=(xh,r0,0)

柱面公式：

(1)

球面公式为

(x+R)2+y2+z2-R2=0

(2)

联立式(1)(2)可得xh。

在平面yOz内直线Oa的方程为

y-zcotφ=0

(3)

其中：φ为三角槽开口角。

缸体通油孔分布圆方程为

(4)

联立式(3)(4)可得到点a坐标(xa,ya,za)。点a、h在缸体通油孔分布圆平面上，且xa=xh。

则可得到直线ah斜率表达式：

(5)

θ=arctan(r0-ya)/za

(6)

其中：θ为直线ah在yOz面的投影角度。

由图1所建立的坐标系可得直线ab、bd、cd、ah的方向向量分别为ad=(-tanβ,sinθ,-cosθ)、bd=(cosα/2、sinα/2，0)、cd=(cosα/2,-sinα/2,0)、ah=(0,sinθ,-cosθ)。

设平面acd的法向量为n，平面abd的法向量为m，则：

ad×cd=n

(7)

ad×bd=m

(8)

已知点a在两平面内，则可根据点法式求出两平面acd、abd方程分别为

-cosθsinα/2(x-xa)-cosθcosα/2(y-ya)+tanβsinα/2(z-za)=0

(9)

cosθsinα/2(x-xa)-cosθcosα/2(y-ya)-tanβsinα/2(z-za)=0

(10)

由点向式求出直线ah方程为

(11)

由式(11)可得：

(12)

设点m(xm,ym,zm)为直线ah上从点a转角φ时的点，对于微型轴向柱塞泵球面配流副，过渡区包角小，可以近似认为

φr0=|am|

(13)

其中：φ为缸体转角，rad，0≤φ≤φ。

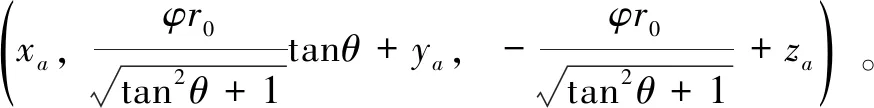
(y-ym)sinθ-(z-zm)cosθ=0

(14)

分别联立式(5)(10)(14)、(5)(9)(14)、(9)(10)(14)可以求出点e(xe,ye,ze)、f(xf,yf,zf)、g(xg,yg,zg)三点坐标。

由球面方程(2)以及式(14)可以求出球面配流盘表面与平面egf的截交线ef在xOy面的投影方程f为

(x+R)2+y2+[tanθ(y-ym+zm)]2-R2=0

(15)

直线ef在xOy面的投影方程g为

(16)

由图3设阴影部分面积为S1，egf三点围成面积为S2，可得过流面积S为

图3 egf截面在xOy平面的投影

S=S2+S1/cosθ

(17)

其中：θ为直线ah在yOz面的投影角度。

S2=1/2|fe×eg|

通过以上分析，三角槽过流面积可以表示为多元函数：

S=F(α,β,φ,φ,R,r0)

根据流体体积模量的定义可以导出控制体积的压力上升率方程，其可以表示[7]为

(18)

式中：E为油液有效体积弹性模量；p为瞬时压力；Vpc为当缸体在进入预卸压区时，密封油缸内包含的油液总体积。在预升压区和预减压区使用相同错配角的前提下，柱塞腔与预升压区最初接触的位置常用φ0-Δφ/2来表示。Vpc可由下式给出：

(19)

其中：V0是活塞位于外死点时活塞室的闭死容积；AP=πd2/4是活塞的横截面积，d是活塞的直径；φ0是错配角；Δφ是预升压区包角；Rf是活塞分布半径；γ是斜盘的倾角。

规定油液流进柱塞腔为负，流出为正。对于文中研究的微型柱塞泵，排量为1 mL/r，相比中大型泵，其排量很小，所以为了提高建模的准确性，柱塞腔与球面配流盘之间的流量泄漏不能忽略。则：

dV=-dV1-dV2+dV3

其中：dV1为缸孔内油液被压缩的体积；dV2为从排油口倒灌进入缸孔内的油液体积；dV3为球面配流副界面泄漏的油液体积[8]。

(20)

(21)

其中：Δp1=pd-p，pd为出口压力。

(22)

(23)

再将dt=dφ/ω代入式(23)得到瞬时压力与转角的关系式如下：

(24)

2 预升压区参数优化

对于文中研究的单向旋转微型轴向柱塞泵球面配流副预升压区，主要结构参数为三角槽深度角β、宽度角α、开度角φ、错配角φ0。对这4个主要结构参数进行优化设计，可以建立以无压差过渡条件下的最小压力梯度峰值为目标的函数[9-10]。

油液流进柱塞腔为负，流出为正，所以压力变化公式(24)可以改写为

(25)

柱塞泵在实际工作过程中，不存在无压差过渡，其中无压差过渡是指最小瞬时压力变化值在小于5%的额定压力范围之内[11]。文中所研究的柱塞泵的额定压力为30 MPa，由此可知，Δp的值应该小于1.5 MPa，最终选取1.2 MPa。

根据高速高压微型柱塞泵球面配流副设计参数及实际实验指标，采用46号液压油[12]，球面配流副的结构参数以及其他相关参数如表1所示[8]。

表1 结构参数以及其他相关参数

根据参考文献[9-10]以及该公司研发该型微型轴向柱塞泵球面配流副的实际工程经验，预升压区三角槽优化参数取值范围如表2所示。

表2 三角槽参数取值范围

令：x1=β，x2=α，x3=φ0，x4=φ，将各参数代入式(25)可得优化目标函数：

(26)

其中：S=F(x1,x2,x4)。

粒子群优化算法(Particle Swarm Optimization，PSO)是一种模拟鸟群捕食行为的群智能优化算法。PSO的原理简单、收敛速度快、计算量小且控制参数较少，因而被广泛应用于各种优化问题[13-14]。

文中采用该优化算法，取种群数为50，分别迭代20、50、100、150次，粒子群优化算法收敛曲线如图4所示，迭代结果如表3所示。

表3 粒子群优化算法迭代结果

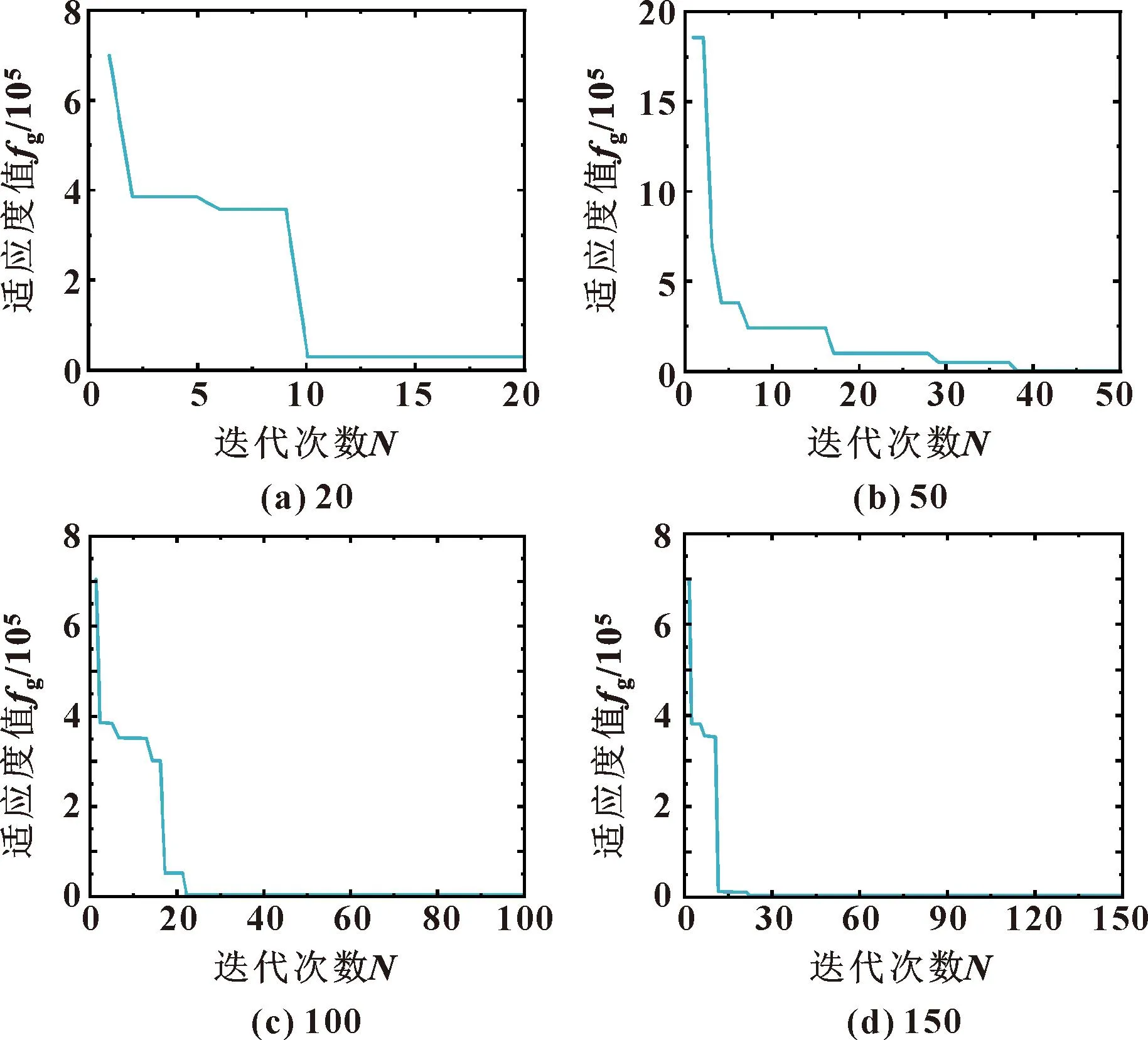
图4 不同迭代次数下收敛曲线

由表3可知：迭代次数达到50时，已经取得最优值。优化结果为：深度角β=16.1°，宽度角α=56.3°，开口角φ=12.7°，错配角φ0=1.2°。

预升压区优化前后的结构参数如表4所示。

表4 优化前后参数

3 仿真分析验证

通过三维建模软件建立该高速高压微型轴向柱塞泵模型，抽取流体域后进行网格划分。仿真的重点在于三角槽，不同于中大型柱塞泵，微型轴向柱塞泵三角槽结构精细，尺寸微小，最大截面尺寸为0.1 mm2级别。为保证仿真的有效性与正确性，其结构不可做简化处理，必须保持完整真实的几何结构特征。需要对三角槽整体进行加密处理，最终得到图5所示的网格模型。

以往对轴向柱塞泵进行仿真时，大多数将油液视为不可压缩流体。实际工况下，压力波通过声音速度传播，所以考虑流体可压缩性可使仿真更加接近真实情况[15]。

对于液体和固体，体积弹性模量E和密度ρ随压力的变化很小，主要受介质的影响，所以在同一介质中，声速也基本上是一个常数。但是如果考虑流体的可压缩性，流体密度将会发生变化，所以有必要将声速考虑进去[16]。文中使用Fluent自带的UDF编程实现油液密度随压力的变化。

由于微型轴向柱塞泵球面配流副三角槽结构尺寸小，油液流动会产生湍流，所以使用κ-ε模型。

分别对表4中的原始结构和优化后的结构进行建模，对比仿真分析。在Fluent中监测柱塞腔压力，得到优化前后预升压区柱塞腔压力变化曲线如图6所示。

图6 优化前后仿真压力变化曲线

引入压力脉动率σ：

(27)

其中：pmax是最大压力；pmin是最小压力。

原始模型压力脉动率为8.2%，优化后压力脉动率为3.6%，压力脉动率降低了4.6%。由此可见，对于文中的过渡区结构优化，建立以无压差过渡条件下的最小压力梯度峰值为目标函数是可行的，优化后的预升压区结构能降低压力脉动率，提高微型轴向柱塞泵球面配流副的配流性能。

4 结论

文中建立了单向旋转微型轴向柱塞泵球面配流副预升压区的三角槽过流面积以及压力的数学模型，并对该区域主要结构参数：三角槽深度角β、宽度角α、开度角φ、错配角φ0进行优化设计。优化后结构参数为：深度角β=16.1°，宽度角α=56.3°，开口角φ=12.7°，错配角φ0=1.2°。结果表明：优化后的预升压过渡区的压力脉动率比原始结构降低了4.6%，提高了高速高压微型柱塞泵工作过程的稳定性，有利于降低配流过程的冲击，同时为提高该泵的动态性能提供了有力的依据。