支架现浇混凝土梁桥抗裂性分析与承载力计算

李 春

（南京永安工程技术有限公司，江苏 南京 210000）

1 支架现浇混凝土梁桥早期抗裂性分析

1.1 支架分层浇筑使用阶段极限状态计算

为对支架现浇混凝土梁桥早期抗裂性能进行分析，需要对支架分层浇筑使用阶段的极限状态进行量化分析。计算正常使用极限状态是根据钢筋混凝土受弯构件的正常使用受力情况，对已经满足承载力要求的构件进行计算，并判断变形和混凝土的裂缝宽度是否小于桥规的限值。当进行验算时，如果验算结果与规范不符，就必须加以修正，直至达到设计要求[1]。受力弯曲构件的开裂截面如图1所示。

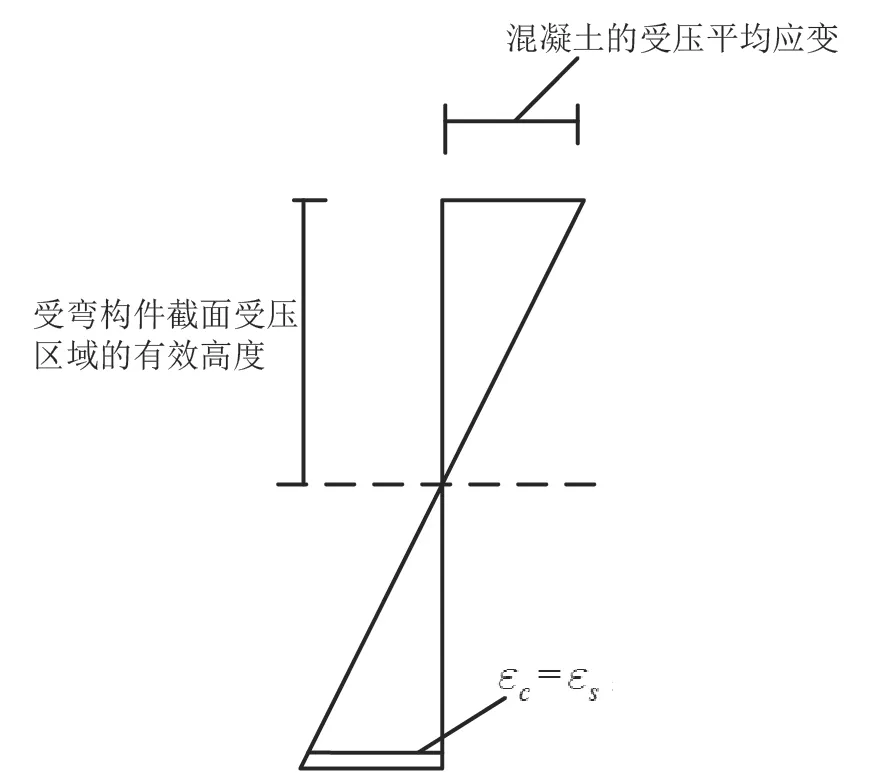
图1 受力弯曲构件的开裂截面示意图

针对钢筋混凝土在受力发生弯折后开裂的构件，对其弹性阶段进行计算。在计算前，设置3个假设条件。

第一个假设：在梁结构发生弯曲变形后仍然保持平面状态[2]。结合平截面假定，得到公式（1）。

式中：ε′c为混凝土的受压平均应变，εc=εs；x为受弯构件截面受压区域的有效高度；h0为梁结构发生弯曲变形位置高度。

第二个假设：弹性体假定。结合平截面的假定得到公式（2）和公式（3）。

式中：σ′c为垂直应力；Ec为28d龄期时的混凝土弹性模量；σc为水平应力。

第三个假设：在受拉作用区域内，拉应力完全由钢筋结构承受[3]。受拉力作用的区域内混凝土结构完全不能承受拉应力。根据上述3个假定条件，得到公式（4）。

εs的取值可以通过应力σs与弹性模量Es的比值得出，因此进一步得到公式（5）。

式中：为钢筋混凝土构件结构横截面的换算系数，的取值可以通过Es与Ec的比值得出。

当计算钢筋混凝土受力构件的正常使用极限状态时，需要对截面进行换算。将两种不同材料组成的截面转变为同一种材料组成的截面受压或受拉过程[4]。图2为截面换算的基本原理图。

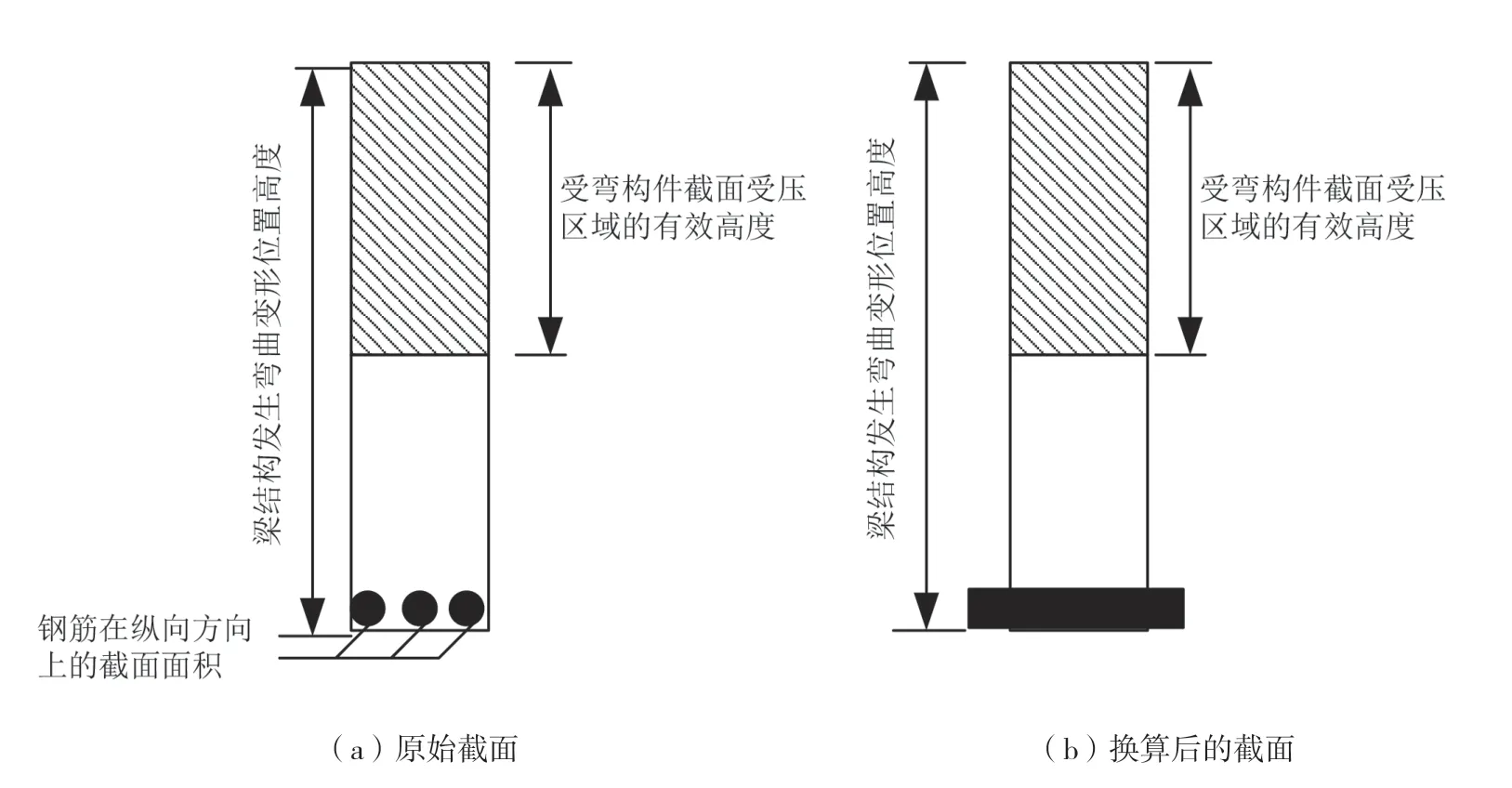
图2 截面换算基本原理图

图2（a）为原始截面，图2（b）为换算后的截面。将钢筋结构的截面面积转换为假定的受拉混凝土截面面积且位置在钢筋的重心[5]。假设混凝土结构所承受的总拉应力与钢筋所承受的总拉应力相同，得出公式（6）。

式中：As为钢筋在纵向方向上的截面面积；Asc为钢筋在横向方向上的截面面积。将公式（6）作为钢筋的换算面积，结合材料力学特征计算换算截面的几何特性[6]。尽管开裂状态下截面均为“T”形，但不同的“T”形截面受压区的高度不同，如图3所示。

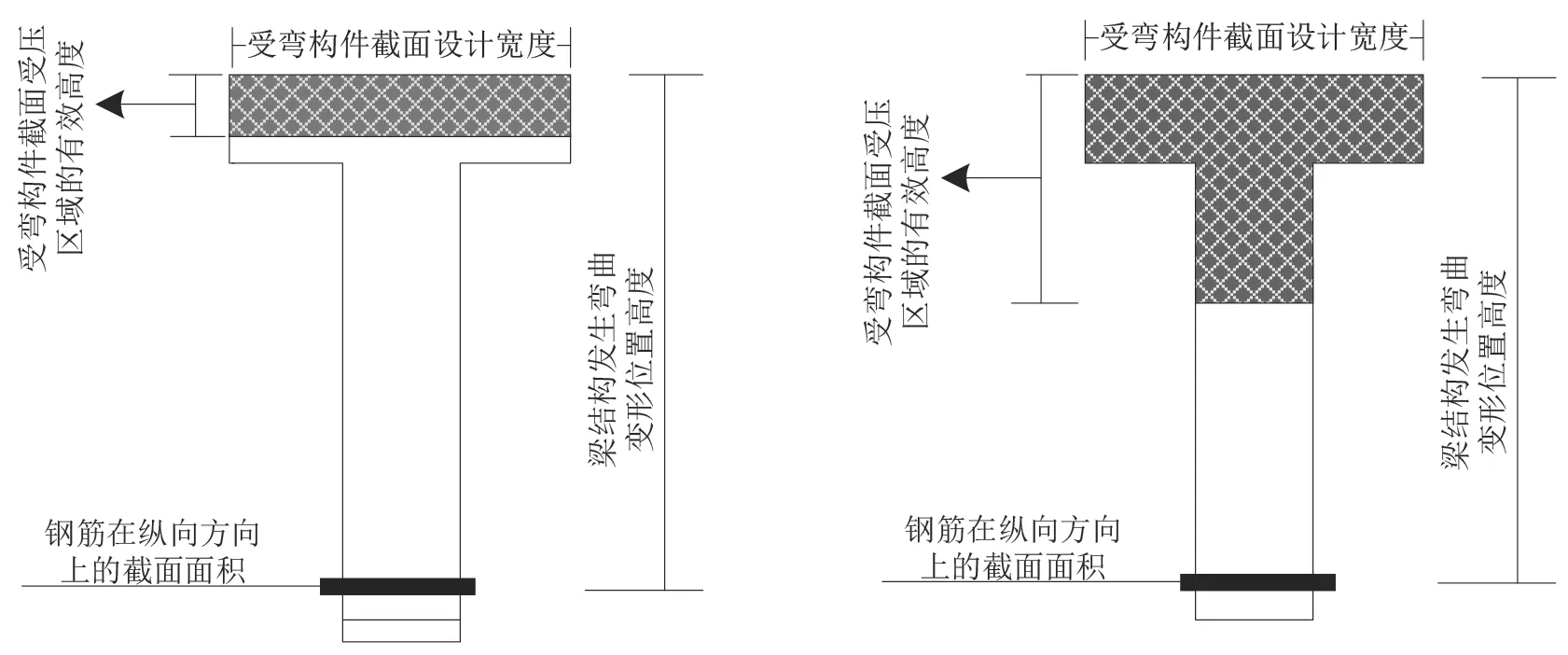
图3 不同开裂状态“T”形截面换算图

从图3可以看出，两种截面均为“T”形，但宽度不同。针对第一种类型，可结合宽度为bf的矩形截面计算其几何特性。第二种类型的受压区的高度如公式（7）所示。

式中：x为受压区的高度；A为纵向受力钢筋截面面积；B为构件正截面宽度。

1.2 支架现浇混凝土梁桥正截面早期抗裂验算

对混凝土的受弯承载力结构来说，如果要保证结构在服役过程中不产生裂缝，就需要对结构的抗裂性能进行校核。对带支撑的现浇混凝土梁桥来说，如果采用了分层浇注的方法，就需要对抗裂性进行校核，包括前浇注层的抗裂性、后浇注层的抗裂性和整个结构的抗裂性。荷载频率遇组合及半永久性组合情况下，在边部混凝土的抗裂试验中，边部混凝土的法向拉应力如公式（8）所示。

式中：M1k为边部混凝土的法向拉应力；M1为后浇砼自重对先浇砼构件弯矩的影响；M1Qk为在施工过程中附加在其结构上的其他作用力所产生的弯矩设计值。

在荷载频率遇组合及半永久性组合情况下，计算在抗裂试验中的边部混凝土的法向拉应力如公式（9）所示。

式中：σst为边部混凝土的法向拉应力；M1Gk为整个构件自重影响所产生的弯矩值；w01为部分构件截面换算时受拉力作用边缘位置上产生的弹性抵抗矩；M2s为频遇组合计算弯矩值；w0为整个构件截面换算时受拉力作用边缘位置上产生的弹性抵抗矩。

1.3 裂缝宽度

由于混凝土构件的抗拉强度非常低，因此产生裂纹时只有小的拉应力。裂纹产生的原因为包括外部的变形和限制因素造成的裂纹、因作用而产生的裂纹（弯矩、剪力、扭矩、张力等）和钢筋腐蚀而产生裂纹。应从理论计算和结构措施两方面控制受力状态下的钢筋开裂。目前，钢筋混凝土受弯构件的裂缝宽度的计算方法可分为两种：基于黏结滑移理论法、无滑移理论法和合成理论法；将影响裂缝宽度的因素引入计算公式中。在此基础上，对矩形、“T”形和“工”形截面的钢筋混凝土构件最大裂纹宽度进行修正，如公式（10）所示。

式中：Wcr为钢筋混凝土构件最大裂纹宽度；c1、c2和c3为3个不同的硬性系数；σss为作用频域组合所引起的构件开裂截面纵向受拉力作用下的钢筋应力大小；C为最外排纵方向上受拉力作用影响的钢筋混凝土保护层的厚度；d为常数。对采用分层浇筑的带支撑的现浇混凝土梁桥来说，当检验最大裂缝宽度时，要参照组合受弯构件的检验方法作一些修正。由于采用分层浇注的方式，第一层梁在二次浇注时就已经具备了一定的强度，因此第二次浇注的混凝土的质量是由第一层梁体和托架分担的。本文采用加权余量法，将第一层浇注的钢筋混凝土梁桥进行二次浇筑，由此可以计算第一层梁所受的内力和内力，从而对极限状态和服役期间的影响做出相应修正。

2 承载能力计算

2.1 正截面抗弯承载力

考虑本文研究的混凝土梁在受力条件下，对应的构件为受弯构件，按照构件的正截面承载力，将其承载力计算问题划分为截面设计计算问题与截面复核设计计算问题，后者是指根据受弯构件的截面形状、尺寸、钢筋类型、钢筋等级、钢筋级别、混凝土强度以及钢筋布置规律，对构件截面承载力或控制截面某个弯矩值进行计算。

受弯构件的截面通常为“T”形截面，以此类典型截面为例，分析其在抗弯条件下的承载力。在极限承载状态下，截面仍处于一种静力平衡状态，此时，截面水平方向的内力总和值为0，截面上任意一点的合力矩值也为0，以此为依据，可以得到在这种条件下的受弯构件截面静力平衡状态方程。如公式（11）、公式（12）所示。

式中：X为受弯构件截面水平方向的内力。

式中：fcd为混凝土结构对应的轴心抗压强度设计参照值；bf为受弯构件截面设计宽度；x为受弯构件截面受压区域的有效高度；fsd为受拉钢筋在纵向方向上的抗拉强度；As为钢筋在纵向方向上的截面面积。

明确受弯构件的静力平衡状态后，应确定混凝土梁桥在现浇施工中采用的是分层浇筑方式。通常，在完成混凝土梁桥的二次浇筑后，梁桥将成型，计算结构中整体构件正截面抗弯承载力如公式（13）所示。

式中：Md为混凝土梁桥结构中整体构件正截面抗弯承载力；M1Gd为混凝土梁桥中构件自重所产生的结构弯矩（此数值通常为固定值）；M2Gd为混凝土梁桥自重所产生的结构弯矩；M2Qd为结构在阶段性作用下，可变组合作用产生的结构弯矩。

2.2 斜截面抗弯承载力

在荷载作用下，受弯构件除了会受力产生弯矩外，通常还会受到剪力作用。对现浇混凝土构件来说，完成正截面抗弯承载力的计算后，当构件受到剪力-弯矩的共同作用时，受弯构件会出现斜截面的损伤，因此，须对受弯构件的斜截面抗弯承载力进行计算。

在斜向方向上，现浇混凝土梁受力破坏以斜向压力破坏、斜向拉力破坏和卸载破坏（减压型式破坏）为主。通常，可以采取截面约束条件和一些结构措施避免斜压和斜拉，但对减压式来说，梁的斜截面剪切力的变化范围较大，因此需要计算其剪切力。3种较为常见的斜截面破坏方式如图4所示。

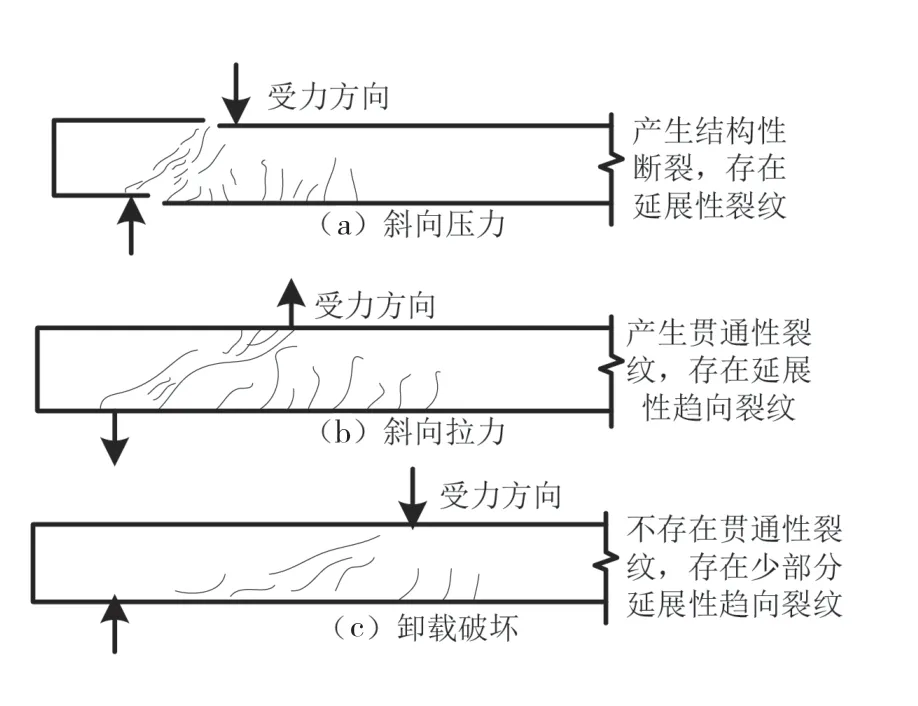
图4 斜向压力破坏、斜向拉力破坏和卸载破坏（减压型式破坏）形态

图4（c）为较典型的减压型式破坏所产生的裂缝，对减压破坏条件下，斜截面抗弯承载力进行计算，如公式（14）所示。

式中：Vu为减压破坏条件下，斜截面抗弯承载力；α1、α2、α3为不同减压破坏条件下的影响系数，取值需要根据具体情况与相关技术规范设定；p为弯起钢筋的总截面面积；fcu，k为斜截面剪力值；ρsv为纵向配筋率；fsv为构件自重产生的剪力值，通常情况下，fsv的取值为常数。参照上述方式，计算斜截面抗弯承载力。

3 结语

在使用混凝土连续梁桥的过程中，严重超载、材料劣化、结构刚度降低等原因会导致箱梁产生裂缝，国内外对此已有很多研究。在支架现浇箱梁的施工过程中，支架的沉降、混凝土分层浇筑时混凝土的收缩差和水化降温，都有可能导致结构裂缝。因此，必须对其原因与发展进行分析，掌握产生裂缝的具体原因，才能及时采取有效的措施对裂缝进行综合处理。虽然现代施工技术力求在最短时间内达到最优，但是微小的作用力会导致较大破坏，为避免裂缝造成梁桥结构性破坏，本文进行了此次研究。

通过研究，明确了要提高箱梁桥的施工质量和承载力，必须对其投入使用后的受力进行全面分析，控制施工过程中对结构有重大影响的因素，对工程项目施工全过程进行受力分析，从而减少现浇箱梁在施工时出现过大应力，保障长期使用的安全性，节省后期的运营和养护资金。