一种加加速度连续平滑的新型柔性加减速控制算法

王树峰，孟新宇，杜毅龙

(沈阳工业大学机械工程学院，辽宁沈阳 110870)

0 前言

加减速控制算法是实现数控机床运动控制功能的关键技术之一，它不仅能够影响数控机床的加工精度，还会对加工效率产生重要影响，因此在数控加工领域，加减速控制技术显得尤为重要。

作为数控机床的重要组成部分，未进行路径规划之前，通过CAD/CAM等制图软件生成原始的路径数据，此时的路径为连续微小线段[1]，而目前应用较多的指数、梯形加减速算法在加工微小线段时加速度会产生突变，从而影响加工的稳定性。传统7段S形曲线算法的加加速度存在突变，因此会引起较大的振动[2-4]，影响加工的精度与平稳性。尽管多项式加减速算法可以确保加速度持续变化，但其计算过程相当繁琐[5-7]。游达章等[8]提出一种改进的四次S曲线加减速算法，该算法虽然能降低加工过程中的柔性冲击，延长电机的寿命，但程序复杂，不易实现。潘海鸿等[9]基于S形曲线规划出17种速度曲线类型，但设计过程过于复杂。王旭浩、张华[10]提出一种非对称S形加减速算法，该算法计算简单，但加加速度曲线依然无法实现连续平滑。高伟强等[11]简化了传统7段S曲线算法，提出了以五次多项式为基础的3段S形曲线控制算法，提高了运行效率，但加加速度不平滑，形成软冲击。叶荫民[12]以三角函数为基础提出的7段S曲线算法确保加加速度的连续变化，但参数较多，算法程序复杂[13-15]，无法保证系统的实时性。

综上，本文作者提出一种新型具有连续平滑加加速度的柔性加减速算法。该算法需要满足数控加工过程中的稳定性要求，其优势通过仿真和实验测试进行证实。

1 新型柔性加减速算法的构建

传统7段S形加减速算法分段多、计算复杂、加加速度突变。为解决这些问题，文中考虑用一段正弦函数拟合加速/减速区间的加加速度函数，而加速度、速度、位移等函数方程通过简单的积分即可以实现。

图1所示为构建的运动控制曲线，由加加速区间(0,t1)、减加速区间(t1,t2)、匀速区间(t2,t3)、加减速区间(t3,t4)和减减速区间(t4,t5)组成，各区间的运行时间满足Tk=tk-tk-1(k=1,2,3,4,5)。

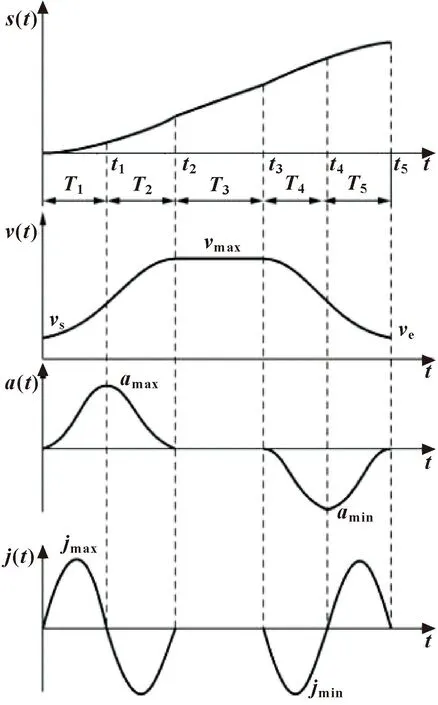
图1 新型柔性加减速算法运动曲线

为满足数控机床的工作要求，应使运动在起点和终点处的加速度都为零，以实现加工的平稳性，因此加加速区间和减加速区间时间须相等，即T1=T2，同理可得T4=T5。

根据图1可以推导出新型柔性加减速算法的加加速度函数j(t)的表达式如下：

(1)

式中：jmax为最大加加速度；k1、k2为比例系数。

对式(1)积分可得到加速度a(t)表达式，如式(2)所示：

(2)

根据式(2)的积分，可以得出速度v(t)的表达式，如式(3)所示：

v(t)=

(3)

式中：vs、vmax分别为初速度、最大速度。

根据式(3)的积分可以得出位移s(t)表达式，如式(4)所示：

s(t)=

(4)

式中：s1表示加速段位移。

根据图1可以确定加加速度j(t)在t=t1和t=t4时为0，因此，加加速段时间T1和加减速段时间T4应满足以下公式：

(5)

设加速段时间为Ta，减速段时间为Td，可得：

(6)

以上为构造的新型柔性加减速控制曲线，只要确定了T1、T3及T4这3个时间参数就可以求解整个加减速控制曲线。显而易见，与传统的7段S形加减速算法相比，该算法不仅能够实现加加速度曲线的连续平滑，而且实现过程更加简单。

2 速度规划

数控机床实际加工过程中线段长度及初末速度是否相等是加减速控制算法中的关键因素。若线段长度较长，机床可达到最大速度vmax；若初末速度相等，则加速区间曲线和减速区间曲线对称。新型柔性加减速算法根据初末速度是否相等以及加工的线段长度求出T1、T3、T4，然后利用上述公式进行速度规划。

2.1 线段长度较长的情况

设线段长度为L，当L较长时，机床可达到最大速度vmax，根据初末速度是否相等可分为以下2种情况。

(1)初末速度相等

由于加速区间和减速区间的运动控制曲线对称，加速段时间和减速段时间相等，即Ta=Td。由式(6)可得T1=T2=T4=T5=Ta/2。由式(3)可以得到：

(7)

由式(4)可求得加速段位移sa，而减速段位移sd=sa，即：

sa=sd=(vmax+vs)Ta/2

(8)

如果L≥sa+sd，即存在匀速段，其时间根据式(9)确定：

T3=(L-2sa)/vmax

(9)

由式(7)—(9)求得T1、T3、T4后，规划的速度及加速度曲线如图2所示。

图2 初末速度相等时规划的速度(a)及加速度(b)曲线(较长线段)

(2)初末速度不相等

当初末速度不相等，即vs≠ve时，由式(7)可知，sa≠sd，同时比例系数k1≠k2，由式(3)可以得到：

(10)

由式(4)可求出加速段位移sa、减速段位移sd分别为

(11)

如果L≥sa+sd，则存在匀速段，其时间根据式(9)确定：

T3=[L-(sa+sd)]/vmax

(12)

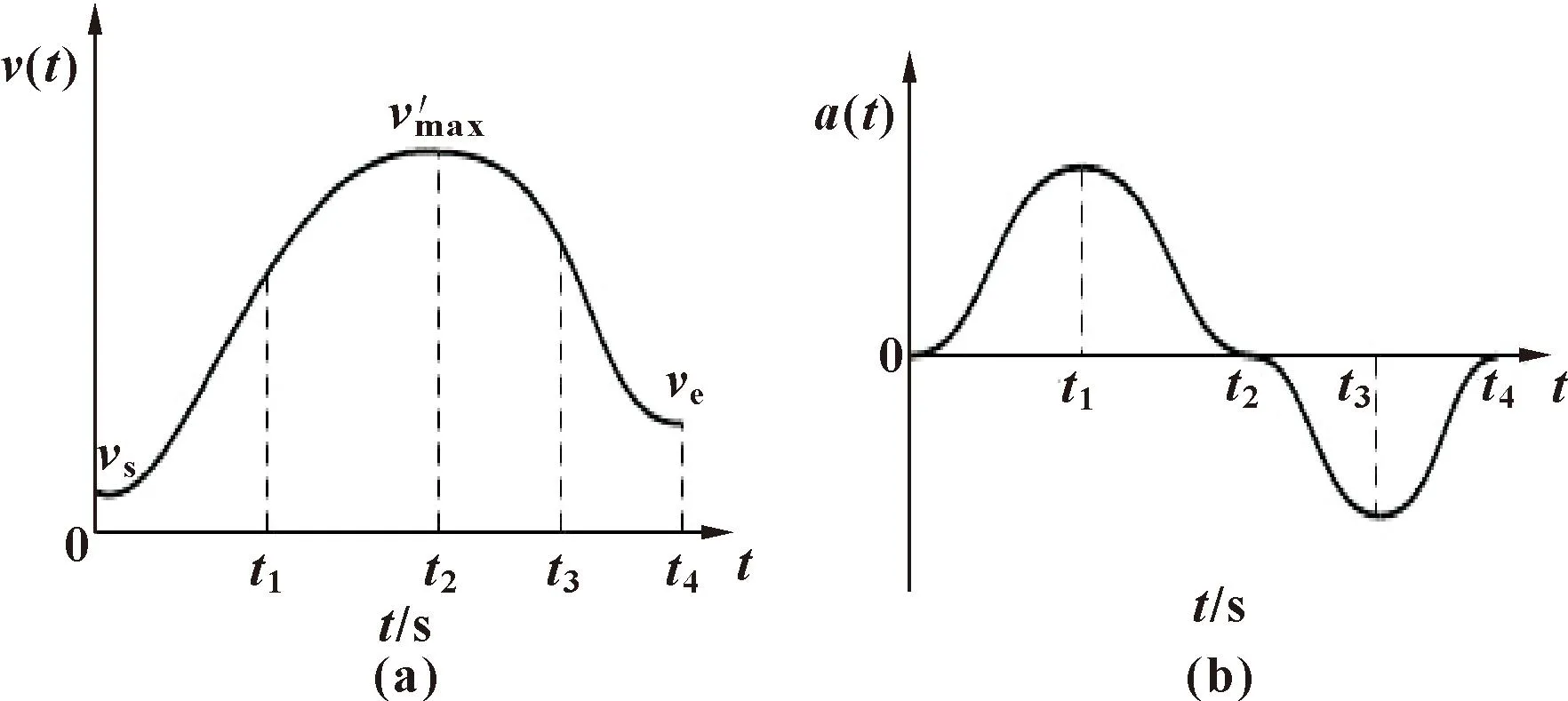
由式(10)—(12)求得T1、T3、T4后，规划的速度及加速度曲线如图3所示。

图3 初末速度不相等时规划的速度(a)及加速度(b)曲线(较长线段)

2.2 线段长度较短的情况

当L

(1)初末速度相等

此时各区间的时间相等，即T1=T2=T3=T4。由于加速段和减速段的位移各为L的一半，根据式(7)(8)可得：

(13)

将式(7)中的T1代入式(13)中可得：

(14)

式中：v′max为实际最大速度。

由于式(14)只存在一个未知数v′max(其余参数均已知)，可采用牛顿迭代法求解v′max，规划的速度及加速度曲线如图4所示。

图4 初末速度相等时规划的速度(a)及加速度(b)曲线(较短线段)

(2)初末速度不相等

由于不存在匀速段，令L=s′a+s′d(s′a、s′d分别为重新规划后加速段和减速段的位移)。s′a、s′d计算公式如下：

(15)

从而有：

(v′max+vs)T1+(v′max+ve)T4=L

(16)

将式(10)中的T1、T4代入式(16)中得：

(17)

式(17)中，由于vs、ve、jmax、L已知，根据牛顿迭代法得到实际最大速度v′max后即可规划出速度及加速度曲线，如图5所示。

图5 初末速度不相等时规划的速度(a)及加速度(b)曲线(较短线段)

3 仿真与测试

文中提出的算法能否实现加加速度的连续平滑以及提高机床加工效率，在MATLAB软件上进行仿真验证，并与传统的S形算法进行对比，算法流程如图6所示。

图6 算法流程

设定实验数据如下：vs=ve=0、vmax=400 mm/s、L=200 mm，最大加速度等于最大减速度，即amax=dmax=5 000 mm/s2，jmax=5×104mm/s3。2种算法的运动曲线仿真结果对比如图7所示。

图7 两种算法的运动曲线对比

由图7可知：相比传统的S形算法，文中提出的算法加加速度曲线连续平滑，能够减小机床加工过程中的振动，提高稳定性。

为进一步验证文中提出算法的可行性和有效性，采用图8所示的基于两正交轴的HIWIN运动实验平台，由运动平台、计算机、驱动器、电压转换器等组成，在计算机上利用C++编程实现控制算法。

图8 HIWIN运动实验平台

对长度在100～200 mm之间的微小线段进行实验验证，从运行时间上对2种算法进行对比，结果如表1所示。

表1 运行时间对比

由表1可知：文中提出的算法相比传统S形算法效率提升了6%以上，因此文中算法更适用于数控机床的连续微小线段加工。

4 结论

针对数控机床加工微小线段时由于加加速度突变引起的振动所带来的稳定性和效率降低等问题，文中提出了一种新型柔性加减速控制算法，推导出其运动曲线方程，该算法分为3个运动时间段，简化了参数，提高了计算效率。实验结果表明：该算法不仅能够满足数控机床加工过程中柔性加减速控制的要求，而且实现了加加速度的连续平滑，有效降低了机床的振动冲击，与传统S形加减速算法相比，能够显著提升数控机床加工过程的稳定性和加工效率。