基于响应面-遗传算法的MCM-BGA 芯片散热优化设计
2024-05-06赵忠伟岑升波邵长春刘织财王致诚
赵忠伟,岑升波,邵长春,刘织财,王致诚
(柳州铁道职业技术学院,广西 柳州 545000)
0 引言
电子封装技术向着微型化、高密度和高可靠性方向发展,同时又要求能满足散热性能好、信号传输快、传输容量大等要求。多芯片组件(Muti-chip Module,MCM)技术是将多个裸芯片和其他元器件组装在同一块高密度多层互联基板上,然后对其进行封装,从而形成高密度、高可靠性、多功能的微电子组件,是实现电子产品微型化、模块化、多功能化的有效技术途径,被广泛应用于军事领域、通信领域、航空航天等电子产品中。然而随着电子封装集成度的不断提高,电子元器件封装密度和功耗也在不断地增大,芯片呈现出高热流密度,高功耗等特点,电子芯片散热问题也越来越凸显[1]。芯片温度过高容易导致芯片一系列失效问题,严重影响电子设备使用寿命,制约着多芯片组件(MCM)技术的发展。
为保证多芯片组件(MCM)工作的可靠性,芯片热设计人员一直致力于研究和准确获取MCM 芯片的在实际工作下的结温,并采用适当的温度来控制芯片的温度,使其不超过芯片热设计最大额定温度,以保证对芯片设计的热可靠性要求。目前对于芯片结温的研究方法主要有数值模拟法、理论模型研究法、实验测试法[2]等。在实验测试法方面,Khatir 等[3]使用光纤传感器在工作期间高压环境下测量芯片温度,以估计功率模块的热阻,但这种方法受限于一定的响应时间差。Dupont 等[4]使用红外热成像仪绘制芯片表面的温度分布图,可以很容易的观察到芯片表面温度的变化,但是通常使用这种方法需要去除芯片的封装外壳和介电绝缘凝胶,并且对红外热成像仪的空间分辨率有较高的要求。
在数值模拟法方面,数值模拟技术集成着越来越多的数值计算方法,比如有限元法(Finite Element Method)、有限体积法(Finite volume method)、有限差分法(Finite Difference Method)、边界元法(Boundary Element Method)等方法使热设计CAD 软件和功能越来越强大。近年来,随着计算机算力的显著提升,数值模拟法越来越广泛应用于电子封装技术的热设计和热管理。商业热仿真软件ANSYS、Flotherm、COMOSOL 等为热设计人员提供了强有力的计算工具,可以准确地模拟出MCM 芯片的三维温度场分布[5-7]。
在芯片结温预测理论研究方面,何成[7]根据芯片结点到壳和结点到板的热阻,建立了双热阻模型,并深入分析双热阻模型的局限性,得到了热阻网络模型误差变化的规律。Cheng 等[8]对多芯片组件的结温进行研究,通过不同方法建立并分析比较了热阻网络模型和热阻矩阵模型,这两种模型方法皆适用于对多芯片组件的结温计算和评估,并发现不同芯片之间安装的位置对芯片的热耦合存在一定的影响。Prope 等[9]发现多芯片封装内部不同芯片间的耦合效应可能不对称,在热稳态情况下可以使用热阻矩阵表示多芯片器件的散热特性。张津源[10]基于线性叠加理论提出了预测叠堆芯片的温度热阻矩阵方法,研究并分析了芯片粘接层厚度、芯片厚度、片面积、芯片层数等因素对叠层芯片散热性能的影响。
综上所述,芯片结温主要研究的方法和手段有实验测量、数值模拟计算、建立芯片结温预测模型。在实际芯片封装工艺中,由于芯片的各项热设计参数的改变,实验测量法和数值模拟法受到一定条件限制,并不能快速得到芯片结温。传统芯片结温预测方法计算精度较高,但是建模较为复杂。因此,在芯片封装过程时,为寻求一种快速高效的芯片结温预测方法,以某通信用的MCM-BGA 多芯片组件为研究对象,构建芯片热设计参数与芯片结温之间的数学模型,并采用遗传算法对该模型进行优化,寻求最优工艺设计参数,以降低芯片结温。
1 MCM-BGA 多芯片三维模型
1.1 MCM-BGA 芯片模型
建立的MCM-BGA 多芯片组件的三维模型主要结构如图1 所示,五个芯片均布在基板上。该多芯片模型主要由七部件组成,分别是PCB 板、焊球、基板、焊料、芯片、导热硅脂、金属封装体的铜散热器。为了便于计算机进行求解计算,将多芯片模型的焊料和焊球进行简化为具有等效热导率的长方体焊料层和焊球层[11]。模型的几何参数见表1。

表1 MCM-BGA 模型几何参数[12]

图1 MCM-BGA 结构示意图
1.2 MCM-BGA 模型的网格划分
采有ANSYS 商业仿真软件建立的MCM-BGA 多芯片有限元模型,如图2 所示。用于计算芯片的结点温度,环境温度为22 ℃,由于芯片的热辐射作用和各层材料之间的接触热阻对芯片的结温作用非常小,因此可以采取忽略[12]。空气自然对流系数为50 W/m2·k,每个芯片均加载2W 的功率,采用芯片体热源加载的方式。MCM-BGA 多芯片有限元模型网格划分为691227 个节点,141000 个基本单元。

图2 MCM-BGA 网格的划分
1.3 MCM-BGA 温度场分析
对芯片进行温度场求解,给每个芯片施加2 W的功率,当多芯片组件的温度场达到一个稳定状态后,多芯片组件的温度仿真云图如图3 所示,芯片结点的最高温度为120.27 ℃,且多芯片组件(MCM)最高温度位于中间芯片处。从图3(a)芯片温度分布可以看出,芯片与芯片之间存在明显的温度场耦合现象,四周芯片温度场与中间芯片温度场热耦合效应最明显,因而使中间芯片的结点温度最高。此外,从温度云图3(a)可以看出芯片温度从中心位置向四周扩散并逐渐降低,最低温度出现在PCB 的四周边缘处。
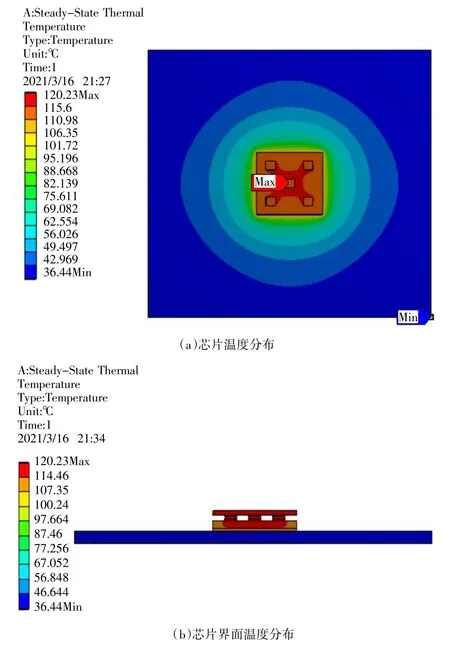
图3 MCM-BGA 温度场的分布
从图3(b)芯片截面温度分布可以看出,芯片工作时产生的热量传递到环境的散热路径主要有两条:一部分热量通过焊料层传递到基板,基板再通过焊球层传递到PCB 板,PCB 通过与外部环境进行热量交换,最终将热量传递到环境;另一部分热量通过导热硅脂传递到铜散热器,铜散热器再通过与外部环境进行热量交换,最终将热量传递到环境。影响芯片热量路径传递的主要因素有环境对流换热系数、基板厚度、基板导热系数、焊料层厚度、封装外壳等因素。芯片通常是封装好的,无法直接测量芯片的结温,因此为尽可能降低芯片结温,热设计人员一致致力于对芯片结温的预测,研究芯片热量路径的传递、并采取合理的措施使芯片结温降低。
2 响应曲设计
2.1 设计变量及响应量的选取
对MCM-BGA 多芯片组件进行响应面模型分析,给每个芯片施加2W 的功率,采用ANSYS 仿真软件模拟出芯片最高温度,并选择空气自然对流换热系数h、基板厚度δsub、基板导热系数ksub、焊料厚度δj这几个参数作为优化设计变量,以多芯片组件中最高结温Tmax为响应变量建立响应面回归方程。模型中各个设计变量的取值见表2。

表2 四个独立设计变量及其取值
2.2 响应面试验设计
响应面方法中主要有中心复合试验设计CCD 和BBD(Box-Behnken Design)两种试验设计方法,CCD适用于多因素多水平实验,有连续变量存在;BBD 适用于因素水平较少(因素一般少于5 个,水平为3个),这里建立的是4 因素5 水平实验,因而采用CCD 设计方法。四个独立设计变量及其响应变量的CCD 设计见表3。
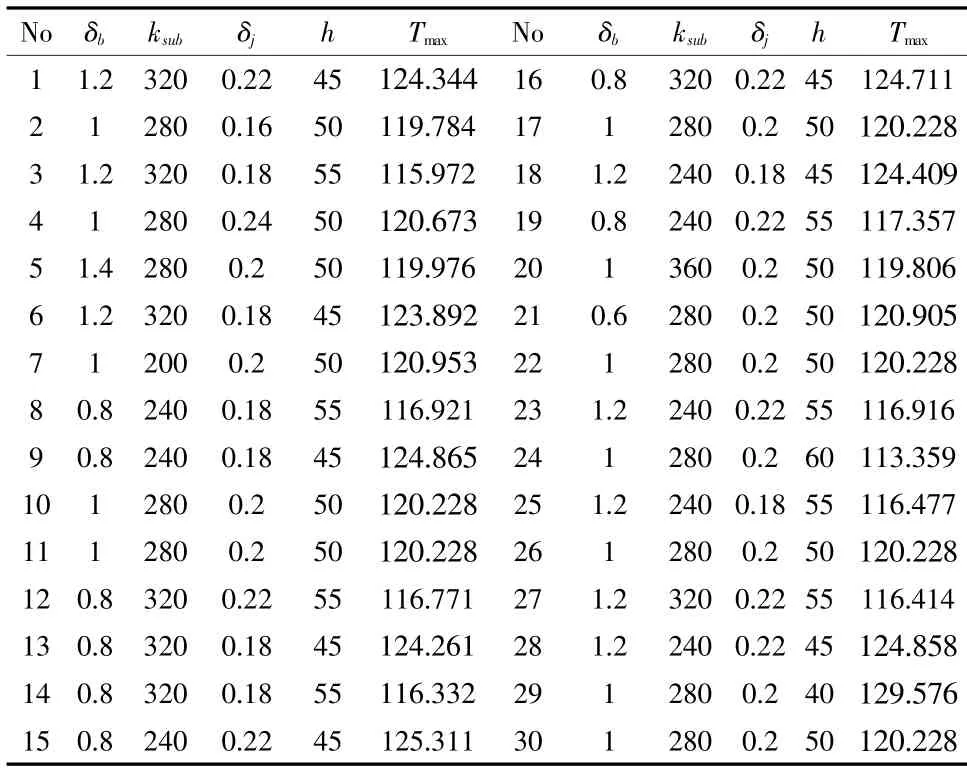
表3 四个独立设计变量及其响应变量的CCD
3 优化设计
3.1 方差分析
四个设计变量的回归系数F值和P值见表4。从表中可以计算得到R2 的大小为0.9931,近似为1,因此可以认为设计变量和响应变量之间的回归方程的线性拟合度是可靠的,显著性高。而对于影响因素来说,P<0.05 时可以认为是显著性的,从表中的模型的P值可以看出,该响应面模型是显著的;从空气对流换热系数h、基板厚度δsub、基板导热系数ksub、焊料厚度δj这几个因素的P值来看,对多芯片组件结温的影响也是显著的。F值表示设计参数对响应量的影响程度,F值越大,影响越显著,可以看出对流换热系数h对MCM-BGA 的结温影响最大,其次是基板导热系数ksub,影响最小的是基板厚度δsub。

表4 四个设计变量的回归系数F 值和P 值
3.2 回归分析
响应面分析中,通常建立近似的线性函数或二阶模型来拟合因素与响应值之间的函数关系式,多项式近似模型的函数分布表示为:
式中:β是未知系数;k为设计变量的数量;Y表示预测的响应值;β0、βi、βii分别表示偏移项、线性偏移和二阶偏移系数;βij表示交互系数。
根据表3,利用Design Expert 软件,可以计算出个参数,即可得如下多芯片结点最高温度的响应面模型:
其中,δsub为基板厚度,mm;ksub为基板导热系数,W/m·k;δj为焊料厚度,mm;h为空气自然对流换热系数,W/m2·k。
3.3 仿真验证
响应回归模型的预测准确度,可以由设计变量与响应变量之间回归方程的估计值与仿真结果进行比较来评价,为全面考察方程预测的准确值,因此,选择一组新的设计点,该组数据与CCD 设计表的数据均不同,通过ANSYS 仿真来验证RSM 的设计结果。响应回归方程的验证见表5。

表5 响应回归方程的验证
由表5 可以看出,响应回归方程的计算值与ANSYS 仿真的最大误差为0.624 ℃,说明该响应回归方程(2)具有较好的线性拟合度,与方差分析的结果一致,对MCM 结温预测的准确性是有效的;从表5 的温度随自变量的变化可以看出,对MCM 芯片结温影响的最大参数首先是空气自然对流系数,其次是基板导热系数,焊料对芯片结温的影响最小,也与方差分析的结果一致。
3.4 基于遗传算法的MCM-BGA 散热优化设计
遗传算法是利用生物进化思想对求解域逐步筛选比较最终搜索得到问题最优解的一种优化算法。本研究把响应面所拟得的回归方程(2)的优化目标函数与遗传算法相结合,将自然对流系数h、基板导热系数ksub、基板厚度δsub、焊料层厚度δj这4 个参数进行优化设计,算法的基本设置见表6。

表6 遗传算法基本参数设置表
遗传算法的基本流程如图5 所示,设置好相应参数后在MATLAB 中运行编辑好的程序进行迭代计算,遗传算法进化过程如图4 所示,当步数迭代到60多步的时候,解的变化基本趋于稳定,多芯片组件的最大结温稳定为111.4 ℃,此时并且得到最优的解。结果表明,当自然对流换热系数为60 W/(m2·K),基板导热系数为320 W/(m·K),基板厚度为1.4 mm,焊料厚度为0.16 mm,MCM 最高结温为111.4 ℃具有最小值,与未优化的MCM-BGA 多芯片组件相比最高结温降低了8.87 ℃,降低了7.375%,具有一定的实际工程意义。因此,对于研究具有与此模型类似芯片散热优化问题,可以采用将响应面法与遗传算法相结合对芯片进行散热优化,同时也可以为其他电子设备热设计提供一种新的思路和方法。

图4 遗传算法进化过程
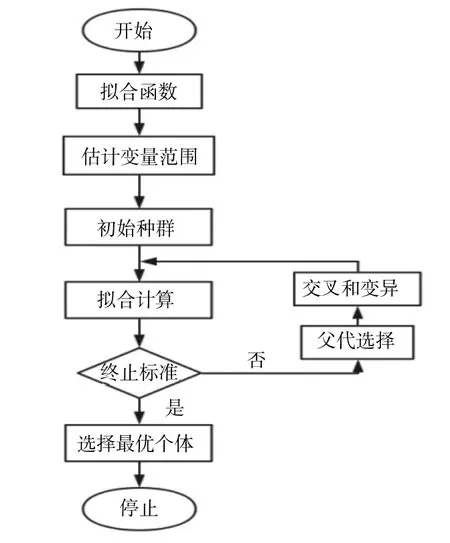
图5 遗传算法的基本流程
4 结语
(1)通过ANSYS 有限元分析获得了MCM-BGA多芯片组件的稳态温度场分布,分析了多芯片组件的散热路径以及影响芯片结温的主要结构参数
(2)建立了MCM-BGA 多芯片组件的响应面模型,分析了自然对流系数、基板导热系数、基板厚度、焊料层厚度对芯片的结温影响,并建立了相应的响应回归方程,验证了其准确性和有效性。
(3)将响应面法与遗传算法相结合对MCM-BGA多芯片组件进行优化设计,当自然对流换热系数为60 W/m2·k、基板导热系数为320 W/m·k、基板厚度为1.4 mm、焊料厚度为0.16 mm 时MCM-BGA 最高结温为111.4 ℃具有最小值,多芯片组件的最高结温降低了7.375%。
