蜡烛火焰振荡行为的实验探究

张杰　张晨　徐术皓　于一真　王新刚

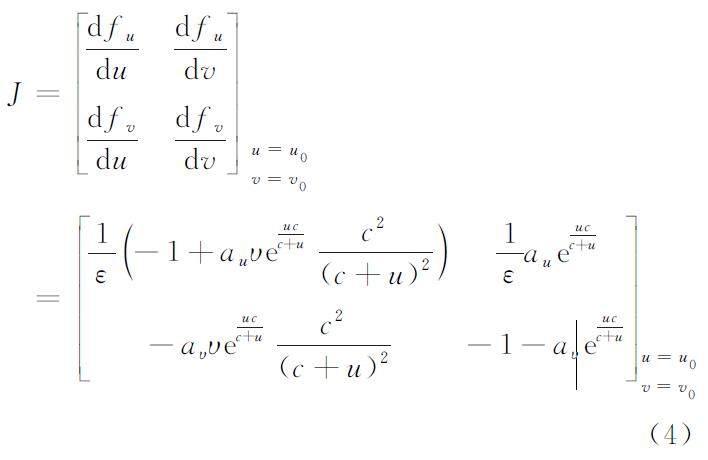
摘 要 燃烧的火焰在一定条件下会呈现出时间上的周期振荡行为，但人们对其背后的动力学机制一直不是很清楚。本文首先利用纹影法对蜡烛的火焰振荡行为进行了实验研究，发现随着火焰尺寸的增加火焰首先从平稳燃烧变为振荡燃烧，之后火焰的振荡频率会逐渐降低。通过简化的燃烧动力学模型，文中进一步对蜡烛火焰的振荡行为进行了数值和理论分析，发现火焰的振荡频率密切依赖于燃料的供应速率和火焰的体积。随着燃料供应速率和火焰体积的增大，火焰首先经历了一次霍普夫分岔进而从平稳燃烧变为振荡燃烧，之后火焰的振荡频率逐渐降低。理论分析结果与实验结论定性吻合。

关键词 火焰燃烧;周期振荡;霍普夫分岔;纹影法

复杂动力系统在一定条件下会自发的涌现出宏观上的周期性振荡行为，典型的例子如大脑神经系统中的各类慢波、连续物理系统中的呼吸子、化学反应系统中的动态斑图、电网系统中的谐波、病毒传播网络中的靶波振荡等[1-4]。分析复杂动力系统中集体振荡行为的产生机制和条件长期以来一直是非线性动力学和复杂系统研究的重要内容之一。本文以蜡烛火焰为例，通过实验观察和理论分析，探究火焰从平稳燃烧变为振荡燃烧的条件，以及火焰尺寸对火焰振荡频率的影响。蜡烛火焰的燃烧不仅呈现出丰富的动力学行为，同时又在工程上有着重要的应用。该实验易于操作，现象丰富，实验结果可以被理论模型定性解释，是学习非线性动力系统分岔行为的一个很好的例子[5，6]。

1 背景介绍

火焰燃烧的动力学行为长期以来一直受到不同领域研究学者的关注，并在实验和理论两个方面开展了大量的工作。考虑到实验的成本和效果，研究中人们经常以单束火苗为对象来研究火焰的燃烧行为。通过控制燃料供应速率（氧气与可燃物）、火焰尺寸、重力加速度、环境压强等因素，人们对火焰的燃烧特征进行了一系列的研究[7-9]。特别地，人们发现当火焰的尺寸低于某一临界阈值时，火焰通常平稳燃烧;然而当火焰的尺寸超过这一阈值时，火焰开始振荡，其振荡频率大致在10Hz左右[10]。上述研究大多基于实验上的观测和对实验数据的分析，缺乏对火焰振荡动力学机制的理解。

理论研究方面，人们根据燃烧反应的流体和热力学特征，提出了不同的火焰燃烧模型[9-11]。这些模型虽然能够定性解释火焰振荡的产生机制，但由于模型中考虑的因素太多，从而使得描述系统演化的动力学方程过于复杂而带来理论分析上的一系列困难。最近，Gergely 等人比较了热辐射和热对流对火焰燃烧的影响[7]，发现相比于热对流，热辐射对火焰燃烧行为的影响可以忽略。在此基础上，作者提出了一个简化的火焰燃烧模型，并在数值模拟中观测到了火焰从平稳燃烧到振荡燃烧的变化。文中虽然观测到了火焰燃烧中的分岔现象，但对于动力学分岔的详细特征缺乏进一步分析。

本文以蜡烛火焰为实验对象，利用纹影法观测火焰的燃烧行为，并通过计算机辅助软件定量分析系统的状态演化。特别地，通过将多根蜡烛捆成一束来调整火焰的尺寸，我们重点对火焰燃烧的分岔行为进行了分析。实验中不仅观测到了火焰从平稳燃烧到振荡燃烧的分岔行为，同时还观测到火焰的振荡频率随火焰尺寸增大而逐渐减小。利用Gergely等人提出的简化火焰燃烧模型，我们对实验结果进行了分析，发现随着蜡烛数目（火焰尺寸）的增加，系统经历了一次典型的霍普夫（Hopf）分岔。进一步，通过对模型进行数值模拟，我们分析了分岔后火焰振荡频率随蜡烛数目变化的关系，发现火焰的振荡频率随着蜡烛数目的增加而逐渐降低。理论分析和数值模拟结果与实验结果相吻合。

2 实验结果

2.1 实验一：蜡烛火焰的振荡现象

我们首先调试实验器材，产生振荡火焰，然后利用纹影法观测火焰振荡时周围气流变化情况，从而增加对蜡烛火焰振荡行为的定性认识。纹影法的工作原理是利用光在被测流场中的折射率梯度正比于流场的气流密度这一机理，从而将流场中密度梯度的变化利用抛物面镜的折射转变为视野中相对光强的变化，使可压缩流场中的激波、压缩波等密度变化剧烈的区域成为可观察、可分辨的图像[12]。

2.1.1 实验装置

实验是在较为封闭的暗环境下进行的，以降低气流对实验的影响和更清楚的观察火焰的振荡现象。用到的实验仪器包括：（1）抛物面镜，如图1（a）所示。（2）高11.7cm、直径0.55cm 的家用照明蜡烛，如图1（b）所示。（3）LED灯泡。（4）蜡烛底座，如图1（c）所示。（5）照相机（手机）和支架。整个实验装置如图1（d）所示。实验中，为保证蜡烛火苗时刻保持在同一高度（便于数据采集），每次实验后对比较高的蜡烛进行裁剪。实验中将5根蜡烛捆扎成一束（排成一圈，中心对称），每根蜡烛均通过蜡油固定在标好位置的底板上。

2.1.2 实验结果

点燃蜡烛并等待火焰达到稳定的振荡状态后，通过手机摄像机对纹影仪中观测到的现象进行记录。如图2所示，火焰的一次振荡近似分为以下四个过程：（1）火焰燃烧加热蜡烛周围的空气，产生温度梯度，使得空气对流，进而在火焰根部产生了由下向上的涡旋。如图2（a）的灰色箭头所示。（2） 随着火焰不断燃烧，涡旋开始上升，火焰向上拉伸，同时火焰腰部开始收缩变细，如图2（b）所示。 （3）火焰继续燃烧，涡旋增大并最终将火焰夹断，上半部分火焰脱离蜡烛，如图2（c）所示。（4）下半部分火焰继续燃烧，火焰高度逐渐变高，恢复到初始状态，如图2（d）所示。根据上述实验观察，我们在图2（e）中画出一个完整振荡过程的示意图。该图有助于加深对火焰振荡行为的认识，为稍后的基于模型的理论和数值分析提供了物理图像。

2.2 实验二：火焰大小对振荡频率的影响

2.2.1 实验方法

我们通过改变蜡烛的数目来调整火焰的尺寸，观察火焰尺寸对振荡行为的影响。考虑到蜡烛束的对称性，在研究中分别考虑1根蠟烛、3根蜡烛、4根蜡烛和5根蜡烛四种情况。对于每一种情况，以60秒为间隔对火焰进行随机扰动。扰动的方式是煽动火焰周围的空气，使得火焰的燃烧明显偏离之前的状态。每次扰动后，我们用摄像机对火焰的燃烧进行拍摄，拍摄的频率是每秒240帧，拍摄的时间为60秒。每一种情况下均采集火焰燃烧视频60次。

接下来对采集到的视频进行处理。首先将每一段视频导入tracker软件，通过软件来追踪蜡烛火焰的振荡。具体方法如下：（1）对原视频图像进行灰度处理并消除背景噪声。（2）以蜡烛的实际宽度和视频中的宽度为基准建立平面直角坐标系，确定火焰的中心位置，如图3（a）所示。（3）利用tracker软件的自动追踪功能追踪视频每一帧中火焰最高点的位置。（4）导出数据并利用MATLAB绘制蜡烛火焰最高点位置随时间的演化曲线，进而统计火焰的振荡频率，如图3（b）所示。在统计火焰的振荡频率时，为了排除暂态带来的影响，统计均从10秒后开始。

2.2.2 实验结果

通过分析四种情况下获得的所有视频，我们分别计算各情况下蜡烛火焰的平均振荡频率。实验结果如表1所示。统计数据显示，当单根蜡烛燃烧时，火焰无振荡;当3根、4根和5根蜡烛捆成一束时，火焰的平均振荡频率分别为10.539Hz、9.997Hz、与9.476Hz。此实验结果初步显示了蜡烛火焰尺寸对火焰的振荡的如下影响：（1）增大火焰尺寸，火焰会从平稳燃烧变为振荡燃烧;（2）继续增大火焰尺寸，火焰的振荡频率逐渐变低。

结合实验一中对蜡烛振荡过程的理解（图2），火焰尺寸对振荡频率的影响可以定性理解如下。蜡烛的数目越多，火焰振荡的气流涡旋越大。但由于火焰核心的温度没有升高，因而其同周围空气的温差没有变化，导致涡旋流动的速度没有发生明显的变化。然而，由于涡旋尺寸的变大，空气对流的速度会变慢，从而导致火焰振荡频率的降低。

3 数值和理论分析

3.1 动力学模型

为了进一步分析蜡烛火焰的分岔行为以及火焰振荡频率对火焰尺寸的依赖关系，接下来我们采用文献[7]中的火焰模型，对蜡烛火焰的燃烧行为进行数值和理论分析。描述火焰燃烧的动力学方程如下

其中，T 表示火焰温度，n 表示火焰中氧气的浓度，C'是气体比热，a（n0）是火焰体积，ω1 是表征温度变化快慢的特征时间，h'是对流热流，T0 是外部温度（室温），β 是单位体积石蜡燃烧的热量，a（n0）是燃料供应速率，E 是活化能，R 是气体常数，ω2 是表征氧气浓度变化快慢的特征时间，n0是空气氧气浓度。为了便于分析，对系统中的参数进行变换，引入无量纲参数

方程中参数av 和au 既与火焰的尺寸相关，也与燃料的供应速率相关。数值模拟中，我们将其他参数设为ε=0.001，c=5.1，τ=1.9，T0=25，γ=2.52×10-3，au =10，并通过改变av 的值的大小来观察火焰行为的变化。定性的分析显示，随着蜡烛火焰尺寸的增大，av 的值将会单调增加。

3.2 数值模拟结果

取av =0.5，图4（a）中画出的是变量u（对应于火焰温度）随时间t 演化图像。图中显示在此参数下火焰平稳燃烧，并未产生振荡。图4（b）中给出的是av =1.5时的模拟结果。该参数下，火焰呈现周期振荡现象，振荡频率大约为20Hz。继续增大参数至av =3.5，图4（c）中显示火焰仍然周期振荡现象，然而振荡频率稍为变慢（大约为18Hz）。上述模拟结果很好地再现了实验中主要的现象，初步验证了理论模型的有效性。

为了系统地研究火焰尺寸对振荡频率的影响，我们将参数av 从0逐渐增加到4，通过数值模拟观察火焰的振荡频率f 的变化。结果如图5所示。从图中可以看到，当参数av <0.74时，火焰平稳燃烧，此时无振荡现象。该现象同实验中的单根蜡烛情况下观测到的现象相似。当av >0.74时，火焰开始振荡，其频率大约为f =8.2Hz。之后，随着av 的增大，火焰的振蕩频率首先稍微变大（0.741）。图5中模拟结果与实验结果（见表1）定性吻合。

3.3 理论分析

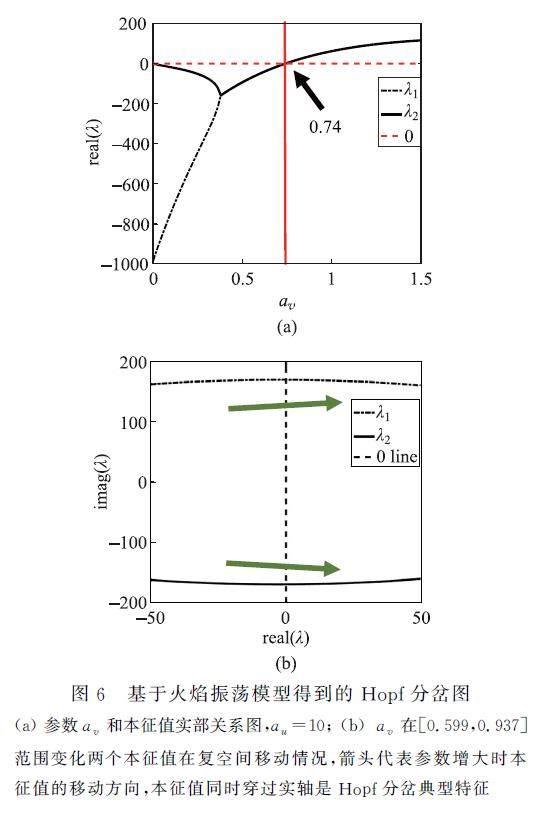
我们最后分析火焰在av =0.74附近的分岔行为。由式（2）可知平稳燃烧状态需满足方程

通过上式得到的平衡态解为（ u0，v0） ，则该平衡态的稳定性由下面Jacobian矩阵的本征值决定：

如果该矩阵的两个本征值其实部均为负（小于0），则该平衡态稳定，否则不稳。图6（a）中画出的是两个共轭本征值的实部随参数av 的变化关系。图中可以看到在av =0.74处本征值的实部从负变正，意味着火焰的平稳燃烧状态在此处失稳。图6（b）中给示的是随着av 的增大两个共轭本征值在的复空间中的变化轨迹。图中可以看到在av =0.74处两个共轭本征值同时穿过实轴。图6显示火焰在av =0.74处的分岔行为属于典型的（亚临界）霍普夫分岔。

4 结语

火焰的振荡燃烧是一个十分有趣的动力学现象，探究其振荡产生的机制以及振荡特征对系统参数的依赖关系是一个非常有意思的课题。本文以蜡烛火焰为研究对象，通过将多束蜡烛捆绑在一起来增加火焰的尺寸，从实验和理论两个方面对火焰的振荡行为进行了分析。研究结果显示，随着火焰尺寸的增加，火焰首先从而从平稳燃烧变为振荡燃烧，之后随着火焰尺寸的增加振荡的频率会逐渐变慢。通过对临界点处系统平衡态的进行稳定性分析，我们发现该处火焰经历了一次典型的霍普夫分岔。后继工作中我们将尝试研究多束火焰之间的集体动力学行为，观察火焰间距、火焰尺寸以及火焰数目对火焰同步行为的影响。

参考文献

[1] AUFINGER L， BRENNER J， SIMMEL F C. Complexdynamics in a synchronized cell-free genetic clock[J]. NatCommun， 2022， 13： 2852. doi.org/10.1038/s41467-022-30478-2.

[2] 欧阳颀. 反应扩散系统中的斑图动力学[M]. 上海：上海科技教育出版社， 2000.

[3] BEGGS J M， PLENZ D. Neuronal avalanches in neocorticalcircuits[J]. Journal of neuroscience， 2003，23（35）： 11167-11177. doi.org/10.1523/JNEUROSCI.23-35-11167.2003

[4] KURAMOTO Y， IKUKO N. Statistical macrodynamics oflarge dynamical systems. Case of a phase transition in oscillatorcommunities[J]. Journal of Statistical Physics， 1987，49（3）： 569-605. doi.org/10.1007/BF01009349

[5] 夏清华，汪秉宏，蒋品群.一个非线性力学问题的讨论[J].大学物理，2003，22（10）：3-3.

XIA Q H， WANG B H， JIANG P Q. A discussion on nonlinearmechamical problem [J]. College Physics， 2003，22（10）： 3-3. （in Chinese）

[6] 寻之朋，李川南，梁汉普，等.燃烧蜡烛水中悬浮现象的研究[J].大学物理，2019，38（5）：39-44.

XUN Z P， LI C N， LIANG H P， et al. Study of the phenomenonof burning candles floating in water[J]. CollegePhysics， 2019， 38（5）： 39-44. （in Chinese）

[7] GERGELY A， BULCSU'S， PAIZS C， et al. Flickering candleflames and their collective behavior[J]. Scientific Reports，2020， 10： 21305. doi.org/10.1038/s41598-020-78229-x

[8] KITAHATA H， TAGUCHI J， NAGAYAMA M， et al.Oscillation and synchronization in the combustion of candles[J]. Journal of Physical Chemistry A， 2009， 113（29）：8164-8. doi：10.1021/jp901487e

[9] CHEN T， GUO X， JIA J， et al. Frequency and phase characteristicsof candle flame oscillation[J]. Scientific Reports，2019， 9： 342. doi.org/10.1038/s41598-018-36754-w

[10] 賈霁.实验研究若干耦合非全同非线性系统的同步行为[D].北京：北京邮电大学， 2019.

[11] ARAYA Y， ITO H， et al. Bifurcation structure of theflame oscillation[J]. Physical Review E， 2022， 33（12）：124104.

[12] 冯天植，刘成民，赵润祥，等.纹影技术述评[J].弹道学报，1994， 2（2）：89-96.

FENG T Z， LIU C M， ZHAO R X， et al. A review onschlieren technique[J]. Journal of Ballistics， 1994， 2（2）：89-96. （in Chinese）