低客流公交运营模式优化方法
2024-04-30果林峰
韩 艳,果林峰,赵 昊
(1. 北京工业大学 北京市城市交通运行保障工程技术研究中心,北京 100124;2. 交通运输部规划研究院 交通安全应急技术实验室,北京 100028)
0 引 言
近年来,我国地面公共交通的客流量逐年下降,传统的公交服务正处于一个更多元、强竞争的客运市场。面对此问题,常见的解决方法例如:发车时刻表优化[1]、大站快车等调度优化[2]等。但是,在乡村地区、城市偏远地区等低客流密度区域中,部分公交线路其乘客的需求位置、需求时间、车辆的发车时间更加分散稀疏,导致常规的优化方法无法适用于低客流公交线路。然而,政府方面仍需满足此区域中居民的基本出行需求,以保障居民公交出行可达性和便利性。此时则需要一种创新性的运营模式,优化并设置更为灵活的站点、线路等。
随着信息技术与交通行业的深度融合,需求响应公交(demand response transit,DRT)作为一种预约化、个性化的出行服务在德国、中国等城市被广泛应用[3-4];有学者提出采用DRT替代传统公交的新思路[5],并对低客流区域的公交运营模式开展研究;谢成辉等[6]、陈燕萍[7]、徐康明等[8]归纳了国内外公共交通的运营模式,推动了我国公共交通的发展;肖景文[9]、詹静[10]分析了城市偏远区域、低客流区域的乘客需求、交通政策等,探讨DRT的可行性;F .M .COUTINHO 等[11]分析并验证了在低密度客流区域使用DRT 的优越性。但在低客流区域独立建设并使用DRT时,常常因线路走向、车票价格等原因,导致DRT与传统公交之间存在客流竞争现象,对传统公交客流造成冲击,运营效率进一步下降。因此,需重新理解低客流地区的出行服务需求,把握公交客流的出行特征,制定合理的分时段式运营策略。
此外,建立DRT需进行特定的站点、线路、调度的规划研究,在DRT的规划问题方面,胡迪等[12]对乘客进行空间分类,提出了D-K-Means聚类规划DRT站点;靳文舟等[13]根据乘客空间位置利用K-Means聚类算法规划DRT站点,以公交运营利润最大为目标建立DRT线路规划模型。现有DRT站点规划方法仅根据乘客二维空间位置规划站点,并采用固定起讫点的方法规划单次车辆线路,未考虑DRT车辆的连续发车调度问题,无法保证车辆在乘客的需求时间内完成接载任务,有损乘客的时间利益。同时,低客流区域的乘客下车地点较为分散,当面对多起讫点的乘客需求时,以往所规划的单一且固定的目的地将无法满足起讫点分散的出行需求。综上所述,目前的研究中缺少同时考虑空间、时间属性的站点规划方法和考虑灵活目的地的车辆线路与调度规划方法。
为解决上述问题,笔者考虑低客流公交客流特征,设计了一种组合运营模式,探讨新型组合运营模式的优化策略;分析组合模式中DRT站点、线路、调度的规划方法,并以北京市公交线路为例进行实证分析。为低客流区域的地面公共交通提供新的优化思路与方案。
1 基于客流特征的组合运营模式
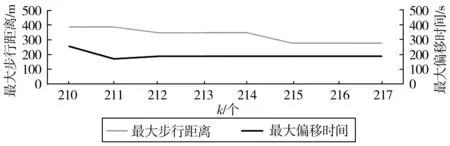
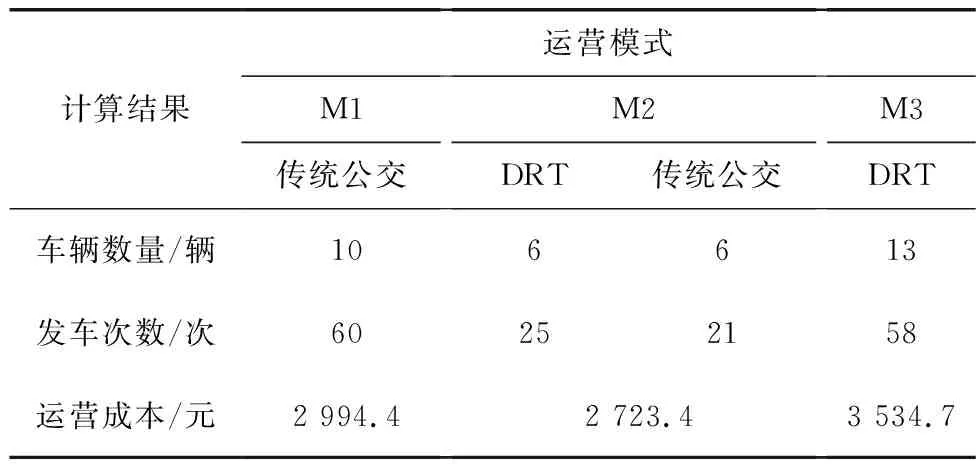
结合低客流区域公交线路客流特征,考虑到部分低客流线路存在高峰、平峰客流趋势,根据客流时空特征,可在不同时段采用不同的运营方案。因此,提出了一种新型组合运营模式:全时段传统公交模式(M1)、分时段传统公交+DRT模式(M2)、全时段DRT模式(M3)。对于客流量Q仍较高(存在客流量Q1表示M1与M2之间的客流量边界值Q≥Q1)的线路,可采用M1;对于客流量Q中等(存在客流量Q2,表示M2与M3之间的客流量边界值,Q2 考虑低客流公交线路客流量、客流时空分布等特性,选用客流量Q、小时客流量PVH、时间不均衡系数Kt3个指标,分析3种运营模式的策略。组合运营模式下的3种模式可描述如图1。 图1 组合运营模式示意Fig. 1 Schematic diagram of combined operation mode 当公交线路的全天总客流量Q1≤Q,并观察平均公交小时客流量PVH呈现为平型趋势,时间不均衡系数Kt趋于1,表明该线路全天仍具有较高的客流量,且客流随时间分布较为均衡。对现有的传统公交进行线路、班次运营优化后,仍采用传统公交即可满足乘客需求,如图1(a)。此时乘客可直接前往车站等候车辆,接受传统公交服务。 客流量Q2 客流量Q≤Q2且PVH呈现为平型,Kt趋于1,表明线路的客流量较低,且客流随时间分布较为均衡。此时客流量较低并已无法通过优化传统公交提高运营效率,此时采用全时段DRT取代传统公交,如图1(c)。此时乘客需进行出行预约,得到信息中心的结果反馈后前往站点等候车辆完成出行。 组合运营模式中包含了传统公交和DRT,因此组合运营模式的实现需对两者分别进行规划研究,从而完成M1、M2、M3的建立。 M1、M2中采用传统公交分别为全天时期、客流高峰时段进行服务,其中M2模式中认为当Kt>1.5时为高峰时段。 传统公交的规划问题经多年的研究,对于公交站点的选择、车辆线路的走向、调度时刻表的优化已相对成熟。因此在采用传统公交的服务时期内,可保留或者优化原有的公交发车计划,调整发车间隔,确保一定的服务水平。 2.2.1 问题描述 M2、M3中采用DRT分别为客流平峰时段、全天时期进行服务,其中M2模式中认为当Kt≤1.5时为平峰时段。 DRT的实现需建立灵活型DRT规划模型,其问题在于如何根据M2、M3的乘客需求,探索DRT的站点、线路与调度规划方法,在考虑乘客时间利益的同时,以最小成本完成乘客的接送任务,如图2。 图2 灵活型DRT示意Fig. 2 Schematic diagram of flexible DRT 2.2.2 DRT站点规划 对于M2和M3中分时段或者全时段DRT,在不同站点、不同时间均有乘客进行登降,需要基于乘客需求进行站点规划,此处站点可分为上车站点和下车站点。 1)三维时空聚类的上车站点规划 关于上车站点规划,不仅需要考虑不同班次传统公交的乘客登降站点位置,还需考虑乘客的到达公交站点的时间,此时的DRT站点设置是考虑传统公交客流空间和时间属性的站点。除考虑乘客空间位置,还需对不同时间范围的乘客进行服务,因此利用K-Means三维聚类算法[15]对乘客进行空间、时间上的三维时空聚类,形成带有时空属性的上车站点。 K-Means三维聚类算法的基本流程:①随机选取k个样本作为初始的类中心点;②计算每个样本与各个种类中心点的距离,把每个样本划分为与其距离最近的类中心点;③当所有样本对象都划分完成,每一类的类中心点会根据类中现有的样本然后重新计算;④重复步骤②、步骤③直到没有中心点再发生变化为止。 计算各个点到中心点间距离使用欧几里得距离计算方法,其计算如式(1): (1) 为确定k值,可利用“手肘法”统计点到中心点的距离平方,即ρ2,并绘制成K-SSE曲线图,观察曲线收敛情况[16]。此外,如图3为避免乘客步行至站点的距离过长,即点至其中心点的平面距离不超过300 m,其计算如式(2): (2) 图3 三维聚类示意Fig. 3 Schematic diagram of 3D clustering 同时考虑乘客的时间利益,聚类结果还应保证乘客希望服务与实际服务的时间偏差,即点至其中心点的纵向距离不超过300 s,其计算如式(3): (3) 2)下车站点规划 关于下车站点规划,根据IC卡数据统计出每一位乘客所对应的下车站点,并将其设置为DRT的停靠站点供乘客下车。 2.2.3 DRT线路与调度规划 在一次运营中,DRT车辆前往不同的站点接载乘客,并根据需求送往不同的站点,该问题本质属于车辆最短路径问题。同时,根据车辆载客量以及一天中所有预约乘客的需求时间进行DRT车辆调度规划,完成一天运营的DRT时刻表编制,该问题实质上属于公交调度问题。文中的灵活型DRT线路与调度规划是利用最少的成本完成乘客的上下行接送任务,将该问题转化为带有时间窗的多目的地最短路径问题与车辆调度问题。 1)模型假设 考虑到路径优化问题的复杂性,在建立模型的过程中做出如下假设: ①所使用的车辆类型、各项指标(额定载客量、车辆行驶速度)均一致;②假设乘客可以在每站时间窗 [ETi,LTi] 开始前到达指定的上车站点;③假设全部车辆从同一首站出发,完成上行任务后回到末站并准备下行任务;④不考虑实际交通流的影响,假设每辆车的车辆行驶速度在整个区域内为匀速行驶。 2)参数定义 3)模型建立 考虑乘客与公交公司双方利益,以公交日运营成本最小为目标,建立灵活型DRT的线路与调度规划模型。 目标函数为: (4) 约束条件为: (5) (6) p≤pmax (7) (8) (9) 10%≤ 100%,k=1,2,…,p (10) (11) 式(4)表示以总运营成本最小的目标函数,由车辆固定成本、车辆行驶成本、时间惩罚成本组成;式(5)表示车辆实际到达站点时间与时间窗的偏离值,用于计算时间惩罚数值;式(6)表示保证车辆按顺序依次到达各个站点;式(7)表示投入使用的公交车不能超过站场所储备的最大车辆数;式(8)表示每一个站点只有一辆公交车停靠;式(9)表示每辆公交车的起点是公交停车站场,即出发站场,目标站点是乘客的不同目的地;式(10)表示每辆公交车的满载率不能大于100%,同时因个别位置偏僻乘客而致使车辆绕行距离过远,在保证其余乘客时间利益的前提下,使得该次车辆的满载率不足10%,则拒绝该乘客的出行申请;式(11)表示车辆的下一班次任务发车时间不能小于上一班次任务完成时间。 4)模型求解 多项式寻求最优解问题通常选用遗传算法、模拟退火算法、蚁群算法等启发式算法进行求解,其中遗传算法具有强大的适应性,且在求解的过程中进行全局搜索,避免了陷入局部最优,能够得到比较满意的最优解,因此采用遗传算法对灵活型DRT的线路与调度规划模型进行求解。 遗传算法的基本流程:①采用整数编码方法进行编码并生成一定数量的初始种群;②对所有个体依次进行选择、交叉、变异操作,得到经过进化后的个体;③计算适应度,保留每一代中最优的个体并记录最优值;④循环上述操作步骤②、步骤③直至达到迭代的停止条件。 其中,编码为了将问题转化为可进行求解的数学形式表达,采用整数编码方案,用0表示公交出发地点,用1,2,3,…,n表示站点编号,用n+1,n+2,…,n+u表示目的地编号。编码如0-1-4-6表示车辆从出发地点依次前往编号为1,4的站点接载乘客,后将乘客送往编号为6的目的地。 选择操作是模仿了生物学进化中的自然选择,主要为挑选上一代群体中适应度高的个体进入下一代,笔者采用操作简单、计算速度快的轮盘赌方式进行选择操作。 交叉操作让种群中个体两两随机交换编码片段,从而提高种群的整体适应度,交叉操作如0-1-4-6,0-2-3-6-5-7两个个体中,“1-4-”片段与“2-3-”片段进行交叉,变为0-2-3-6,0-1-4-6-5-7。 变异操作使个体的片段发生突变,从而产生新的个体,可以使算法在一定情境下跳出局部最优解,变异操作如0-2-3-6-5-7个体中,片段“2-3-”变异为“1-3-”,变为0-1-3-6-5-7。 适应度则是指个体在自然环境下的生存能力,是衡量个体能够保留遗传至下一代的数值标准,适应度的计算函数则取目标函数值的倒数,其表达式为: (12) 为研究方案与模型的有效性,选取了北京市大兴区境内公交线路“兴34路”为案例进行仿真,根据线路信息,兴34路全长11.7 km,共有22个站点,现状发车时刻表中共使用传统公交车10辆,全天共发60班次。 利用兴34路2021年6月9日的公交IC卡数据,兴34路的客流量Q为1 054人/天,平均小时客流量PVH为75人/h,平峰时段PVH为24人/h,处于较低水平。根据IC卡数据计算时间不均衡系数并将系数大于1.5的时段07:00—09:00、17:00—19:00视为客流高峰时段;06:00—07:00、09:00—17:00、19:00—22:00视为客流平峰时段。同时为了对比3种运营模式的优劣,分别利用M1、M2、M3对兴34路进行优化。 3.2.1 站点规划 首先根据IC卡数据以及兴34路线路站点信息随机模拟出乘客在使用DRT出行时的出发位置,并将每个乘客的出发位置与其出发时间进行匹配,形成乘客出行的需求点。 1)上车站点规划 在 MATLAB 软件中利用K-Means三维聚类算法对需求点进行三维时空聚类,并分别计算不同k值下的乘客到各中心点距离并绘制K-SSE曲线,利用“手肘法”观察K-SSE曲线收敛情况,并绘制最大步行距离以及最大时间偏移量曲线。 以M3模式上行乘客结果为例,如图4、图5,当k取到215个时,K-SSE曲线逐渐收敛并趋于稳定,且最大步行距离小于公交站点服务覆盖半径300 m要求,时间偏移量小于300 s,故M3模式在不同时间的DRT站点共215个。同理,M3模式的下行上车站点为206个;M2模式上行上车站点为94个,下行上车站点为98个。 图4 K-SSE曲线Fig. 4 K-SSE curve 图5 不同k值对应的最大距离与时间偏移量Fig. 5 Maximum distance and time offset corresponding to different k values 2)下车站点规划 根据IC卡数据,统计乘客的下车站点,即乘客出行的目的地位置,兴34路共22个下车站点。 3.2.2 线路与调度规划 传统公交部分按原计划进行,DRT部分则在MATLAB软件中搭建遗传算法,种群数量为200,进化代数为20 000,交叉概率为0.7,变异概率为0.1,最大车辆数pmax为15辆,每辆车的额定载客量Q0为25人,根据车辆购置费与使用寿命,每辆DRT车的使用成本c1为50元/辆,每辆传统公交车的使用成本为60元/辆,车辆单位油耗成本c2为2元/km,根据IC卡测算,车辆平均行驶速度v0为25 km/h,单位时间惩罚成本c3为0.5元/min,DRT上车站的点时间窗范围为前后5 min,DRT与传统公交的乘客到站规律均服从正态分布。 兴34路M1、M2、M3的仿真实验结果如表1。 表1 不同运营模式的计算结果 1)车辆数量p:M1使用10辆传统公交车;M2使用6辆DRT车、6辆传统公交车;M3使用13辆DRT车。 2)发车次数:M1、M2、M3分别发出了60班次、46班次、58班次。 3)运营成本Z:M2的Z为2 723.4,相比M1、M3分别降低了9.0%、23.0%。 综合考虑仿真结果,最终推荐M2为优化兴34路的最佳方案。M2下的兴34路发车班次如图6。在06:00—07:00、09:00—17:00、19:00—22:00时间段内采用DRT进行服务,在07:00—09:00、17:00—19:00时间段内采用传统公交进行服务。 图6 M2下兴34路发车班次Fig. 6 Departure frequency of Xing 34 route under M2 在M2中,高峰期间的客流量约占全天客流量的70%,传统公交能够拥有充足的客流以保障高效运营,平均发车间隔为12.0 min;平峰时段根据数量较少且分布广泛的乘客需求制订DRT发车班次以及行驶计划,平均发车间隔为25.7 min。相比兴34路的原始方案M1,共减少14班次。M2中的两种服务相互配合,更加契合低客流区域的公共交通发展趋势。 针对低客流公交线路提出了基于客流特征的传统公交与DRT组合运营模式优化的新思路,首先基于客流时空分布特征,分析了组合运营模式的策略选择;结合车辆路径问题与灵活型DRT的特点,建立了规划模型,利用K-Means三维聚类算法与遗传算法进行求解;最终结合案例,分析了低客流传统公交进行优化的方案,针对日客流量1 000人次的公交线路,M2相比M1、M3分别提高了9.1%、22.9%的整体性能,验证了组合运营模式的可行性。本研究可为类似特征的低客流公交线路提供优化方案。 笔者在研究的过程中,未考虑原始传统公交乘客向组合运营模式的转移意向,同时,仅针对一条线路进行仿真实验。在后续研究中可对不同客流特征(客流量Q、小时客流量PVH等) 、不同线路特征的线路进行仿真实验,探讨在不同乘客转移意向下的不同运营模式适用边界,进一步研究文中M1、M2、M3之间Q1、Q2的取值问题,从而得到更加普适化的结果。
1.1 全时段传统公交模式
1.2 分时段传统公交+DRT模式
1.3 全时段DRT模式
2 组合运营模式规划
2.1 传统公交规划
2.2 DRT规划




3 案例分析
3.1 基于客流特征的组合运营模式优化
3.2 灵活型DRT规划模型

3.3 结果分析

4 结 语
