基于非均质雷达图谱的沥青路面结构损伤识别技术

洪小刚,张伟光,王浩仰,田宏宝

(1.山西高速公路工程检测有限公司, 山西 太原030008; 2.东南大学 交通学院, 江苏 南京 211189;3.中公高科养护科技股份有限公司, 北京100095; 4.云加一科技有限公司, 湖北 武汉430205)

0 引 言

目前我国高速公路网已日趋完善,约60%的服役年限达到或超过8年。随着服役年限的不断增加,在繁重荷载与复杂环境作用下,沥青路面结构逐渐出现破坏,如结构裂缝、层间不连续、不均匀沉降等[1]。此类病害无法从表面直接观测,若不及时采取措施会加快路面整体结构的破坏,影响行车安全性与舒适性。探地雷达作为一种高效、连续、无损检测技术,近年来被广泛应用于路面结构层厚度与内部病害的检测。高频电磁波在路面结构内部不同电性介质会产生反射,通过分析目标回波波形、幅值、走时等特征,从而推断出隐性病害的位置、形态与介电特性[2]。然而,采用探地雷达进行路面结构损伤检测时存在两个问题:

1)当前研究多将结构层简化为层状均质体系,雷达波仅在不同结构层分界面及目标体处发生反射。而实际传播过程中,集料、沥青胶浆、孔隙等材料的电性存在差异,雷达波在结构层中会频繁发生反射并造成扰动,致使能量衰减灰度暗淡,与实测雷达剖面图的回波特征不符[3]。

2)为解决人工检测效率低、精度差等问题,采用深度神经网络自动辨识雷达图谱已成为当下主流[4-6]。但由于雷达图谱数据集较少,在数据集构建时常采用数值模拟批量生成目标在图谱上的回波特征[7]。而匀质模型获取的图谱特征与实测数据存在差异,若采用匀质图谱来训练模型可能会导致网络结构的特征提取能力不足,从而导致结构病害的自动检测精度低下。

为解决上述问题,笔者开展基于“沥青-集料”二相介质图谱与实测图谱融合的沥青路面结构病害自动辨识技术研究。采用IDS雷达系统检测沥青路面内部裂缝与层间不连续两类病害,获取实测剖面图异常回波特征;基于芯样CT扫描图,在gprMax软件中构建“沥青-集料”二相介质模型,融合仿真图谱与实测图谱分别构建两类数据集;并采用YOLO v5深度神经网络对两类数据集进行训练,在实测图谱组成的测试集上进行模型识别结果的性能评估。研究结果表明二相介质模型数值模拟的图谱特征可提高模型识别的准确性。

1 雷达剖面图数据集构建

1.1 实测剖面数据采集

选用IDS探地雷达采集沥青路面结构损伤数据。依据路面结构、病害类型与深度,采集参数设为:采样点512个,时间窗20 ns,天线中心频率为900 MHz,有效检测深度约为0.8 m,测量精度可至厘米级。精度与深度均能够满足沥青路面结构损伤的检测要求。

结构裂缝与层间黏结不良(松散破碎、层间不连续)是沥青路面常见的结构病害,在雷达图谱中的回波特征存在显著差异。图1为沥青路面结构裂缝与层间黏结不良的典型雷达图谱,图1(a)为基层反射裂缝在图谱中的回波特征,表现为上下平行的多个开口向下双曲线组,两翼开口较窄,顶部振幅较强,且穿过层位回波同相轴时有间断;图1(b)为结构层材料松散破碎的回波特征,表现为均匀连续的层间界面出现显著抖动模糊或突然断开;图1(c)为层间不连续的回波特征,表现为“白-黑-白”类梯形同相轴,两端绕射不显著,同相轴灰度增强。由于层间黏结不良在实测中多表现为层间不连续,因此笔者主要针对结构裂缝与层间不连续这两类病害进行研究。

图1 不同类型病害在雷达图谱上的回波特征Fig. 1 Echo features of different types of diseases on GPR maps

1.2 病害回波特征数值模拟

1.2.1 匀质模型

沥青路面结构由沥青面层、水稳基层与土基组成,考虑裂缝与层间不连续常发生在面层与基层,笔者仅建立沥青路面面层与水稳碎石基层模型,面层介电常数设为6,基层介电常数为12。

裂缝数值模型:设计5种宽度(1.0、 1.5、 2.0、 2.5、 3.0 cm)与8种长度(裂缝顶端距离路表面1.0、3.0、 6.0、 9.0、 13.0、 17.0、 27.0、 37.0 cm),宽度与长度可相互组合,共40种裂缝模型,包含面层裂缝与基层贯穿裂缝。层间不连续数值模型:设计9种宽度(1.0 、1.5 、2.0 、2.5 、3.0 、3.5 、4.0 、4.5 、5.0 cm)与32种长度(层间不连续位于模型中央向左右均匀延伸,每间隔5 cm设置一个长度,5～30 cm),宽度与长度可相互组合,共288种层间不连续模型,布设在面层与基层之间。激励源选择Ricker子波,设置收发一体天线,中心频率选用900 MHz,与实测一致。模型深度0.42 m(0.02 m空气层+0.2 m水稳基层+0.18 m沥青面层+0.02 m空气层),时间窗为12 ns,网格步长1 mm。

裂缝与层间不连续数值模拟的部分雷达图谱特征如图2。数值模拟的裂缝回波特征呈两个上下平行的开口向下双曲线,顶部反射波幅值较强,底部反射波幅值较弱且开口窄,反射波幅值随裂缝长度增加而增强;数值模拟的层间不连续回波特征呈开口向下,曲率较缓的双曲线,双曲线顶部振幅强,两侧绕射不显著,当层间不连续长度发展时,双曲线将逐渐呈梯形状。

图2 结构病害匀质Fig. 2 Homogeneous maps of structural diseases

由数值模拟结果可知,裂缝与层间不连续在匀质模型中的图谱特征与实测图谱存在一定差异,这是由于在匀质模型中,裂缝顶底部间的介电常数不变,雷达波仅在顶部与底部两处发生反射,而实际情况中路面材料为沥青、孔隙、集料组成的多相混合物,雷达波进入裂缝内部后因各相材料介电常数存在差异会产生多次反射。

1.2.2 “沥青-集料”二相模型

为获取雷达波在非均质结构层内传播的真实图谱,开发基于图像处理的多相材料建模方法。在输入图像中以不同灰度值区分各相材料,通过点击表征不同材料组分的颜色区域的顺序进行介电常数赋值,再将图片左下角与右上角坐标引入电磁差分模型中,开展“沥青-集料”二相介质的雷达波数值模拟,具体建模流程如下:

1)输入图谱数据增强:采用裁剪、旋转、拼接等方法对输入图像进行增强,满足集料实际粒径与图像在结构层中的真实厚度,如图3。

图3 “沥青-集料”二相介质模型Fig. 3 "Asphalt-aggregate" two-phase medium model

2)图像二值化处理:采用ImageJ软件对芯样图片进行二值化处理,基于图像灰度范围设定阈值将像素划分为两类,如图3(b)。RGB(0,0,0)即黑色区域,表征集料相,RGB(255,255,255)即白色区域,表征沥青相。

3)介电常数赋值:在gprMax软件中依次点击不同颜色区域对集料与沥青两相进行分类[8]。路面材料均为非磁性材料,磁导率与损耗分别为1与0,胶浆与集料的介电常数[9]分别为3与8,电导率分别为0.005与0.001,如图3(c)。

4)逐坐标图片引入:依据扫描图左下角坐标信息构造路面结构层的长度与厚度。扫描图在模型中的长度与厚度,可依据模型网格大小与图像像素比的乘积进行计算。沥青面层扫描图谱像素为1 000×180,左下角坐标设为(0,0.220,0.001),网格大小为0.001。引入模型后表征面层的长度为1.0 m,厚度为0.18 m,右上角坐标为(1.000,0.400,0.001)。

裂缝与层间不连续两类病害在二相介质模型中的回波特征如图4。与匀质模型获取的图谱特征相比,裂缝上下平行的双曲线间存在多次反射,且两翼极窄,这与实际图谱中的裂缝特征更相似。

图4 “沥青-集料”二相模型图谱Fig. 4 "Asphalt-aggregate" two-phase model graph

对比分析匀质模型与“沥青-集料”二相模型数值模拟的图谱特征可知,雷达波在非均质中会发生小尺度的随机散射,导致剖面图产生随机扰动,可表征实测情况下的噪声干扰。因此,采用二相介质获取的仿真图谱较传统匀质模型更符合结构病害在实测图谱上的回波特征。

1.3 病害回波特征标注

在LableImg标注软件中,采用矩形框标注病害回波在图谱上的具体位置,并分配各回波对应的病害类别标签,裂缝和层间不连续回波特征的类别标签分别为crack和interlayer discontinuity(ID),获取矩形框对应标注信息的xml格式文件。将病害标签转化为Class_id,裂缝编码为(1,0),层间不连续编码为(0,1),框对角线两点坐标转化为矩形框中心点坐标、宽与高的归一化值。

将数值模拟获取的图谱数据划分为两组,并添加相同的实测图谱共同组成网络初始数据集。匀质图谱构建的数据集为图谱数据集1#,二相介质图谱构建的数据集为图谱数据集2#。对数据集进行预处理以增加数据集中的图谱数量。最终共标注了1 584张雷达图谱,实测图谱563张,仿真图谱1 021张。裂缝回波特征共893个,仿真图谱437个,实测图谱456个,层间不连续共1 146个,仿真图谱520个,实测图谱626个。为满足网络训练要求,数据集以7∶3的比例随机划分为训练集(1 108张图谱,裂缝625条、层间不连续802个)与测试集(476张图谱,裂缝268条、层间不连续344个)。

2 深度学习算法模型

2.1 网络架构

YOLO模型只需遍历图谱数据集一次,即可直接输出目标位置、类别与置信度,被广泛应用于目标检测工作中。笔者采用YOLO v5算法对两类雷达图谱数据集进行训练。模型由输入端、Backbone、Neck与预测端等部分组成,具体架构如图5。

图5 YOLO v5网络架构Fig. 5 YOLO v5 network architecture

模型输入端基于Mosaic数据增强方法,对输入图像进行随机缩放、裁剪、旋转以增强数据集。Backbone由Focus结构与CSP卷积神经网络所组成,以提取浅层维度的图谱特征。Neck结构由FPN特征金字塔网络与PAN路径聚合网络两部分组成,对浅层特征进行增强,为病害检测提供丰富的位置和语义信息,提高模型的检测精度。输出端基于损失函数的不断迭代,以输出一个与标注锚框近似的预测边界框。

2.2 损失函数

网络训练本质是损失函数不断迭代达到最优解的过程,即要求预测框的位置坐标、置信度与类型概率能无比接近真实框。因此,YOLO模型中的损失计算主要由预测边界框位置误差、置信度误差与类别误差共同决定。

置信度误差在模型中采用广义交并比GIoU进行评价,可由式(1)表示:

(1)

式中:C为包含真实与预测框的最小框;A为真实框;B为预测框;C(A∪B)为包含最小框减去真实与预测框的并集;IoU为交并比。

2.3 评价指标

当完成数据集与网络结构搭建后,需采用相应指标来评价网络识别的效果。分类问题常采用mAP与F1分数进行评价。P-R曲线描述了准确率随召回率的变化趋势,曲线与横坐标召回率围成的面积为平均精度AP,裂缝与层间不连续两类病害的均值定义为均值平均精度mAP。由于P-R曲线是以IoU=0.5为界限计算而来,故将均值平均精度表示为mAP@0.5。

(2)

(3)

模型准确率与召回率的加权平均F1分数可用于评价二分类模型的准确度。F1值越大,表示模型检测精度越高,可由式(4)表示:

(4)

式中:P为查准率;R为召回率。

3 模型训练与验证

3.1 参数设置

模型的工作流程均在PyTorch框架下完成,计算机参数为Inter(R) Xeon 6226R CPU,RAM 128 GB与NVIDA GeForce RTX3090 24 GB。

为适应网络对输入图谱的像素要求,将每张图谱的分辨率分割为640×640像素,满足YOLO模型输入图像的尺寸应为32像素的倍数,输入图像的实际尺寸为15.8 m×0.6 m。由于本中数据量较少,选择COCO数据集训练的初始权重,迁移到模型进行训练。训练200个epoch,每次迭代批量输入8张图片,初始学习率为0.001,动量为0.843,权重衰减为0.000 36。

3.2 模型训练

两类数据集在YOLO v5模型中的训练结果如图6。在前75个训练轮次中,损失值迅速下降。当模型训练100轮后,损失下降趋于稳定,在极小范围内反复震荡,并未出现上翘,模型收敛未过拟合。均值平均精度mAP@0.5在训练集上呈先上升后趋于稳定的变化趋势。对比两类数据集,采用二相介质模型获取图谱的训练损失下降较快。采用匀质图谱训练mAP@0.5在197轮次达到最大值0.971 4,而采用二相介质图谱训练188轮后精度最高,为0.988 1。

图6 两类数据集的训练结果Fig. 6 Training results for two types of datasets

4 结果分析

采用未经模型训练的测试集图谱评估模型的检测性能。采用数据集2# 训练后测试集上的mAP@0.5在148轮次达到最大值,为0.963 3,数据集1#的mAP@0.5在163轮次达到最大值,为0.937 9,此时模型迭代至最优权重。数据集2# 的F1分数为0.938,数据集1# 的F1分数为0.913。采用二相介质图谱训练模型后的mAP@0.5与F1分数值均大于匀质图谱的测试结果,可见采用二相介质图谱训练YOLO v5模型后的检测精度更高。两类数据集在不同网络中的测试结果如表1,采用YOLO v5模型检测雷达图谱的mAP@0.5最高且浮点操作最少,验证了模型的优越性。

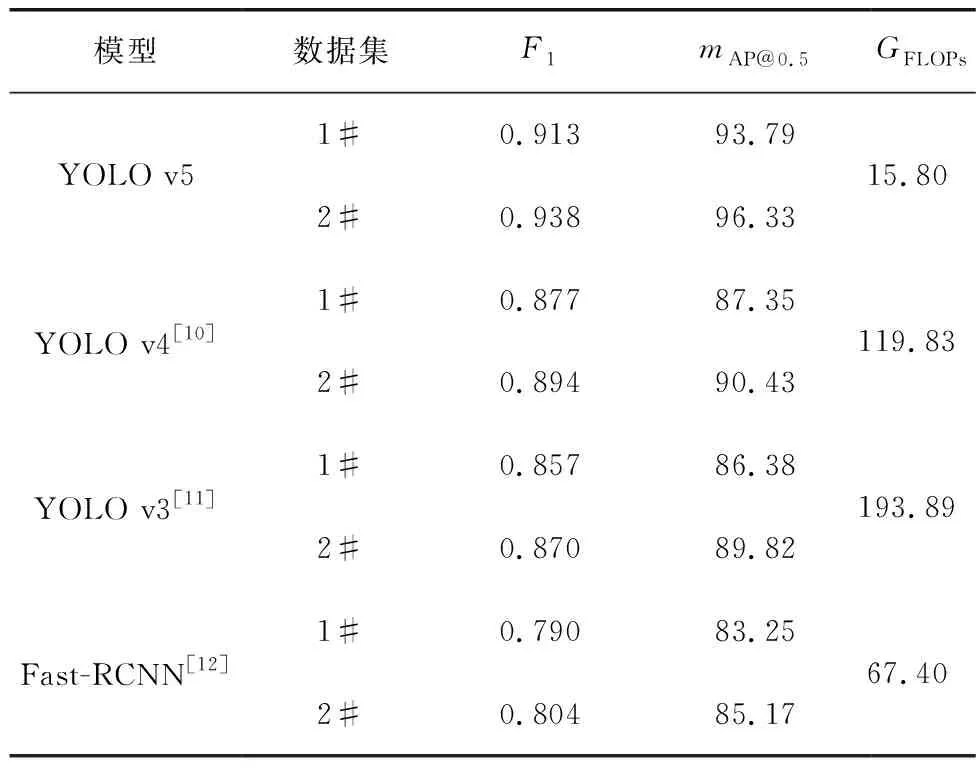
表1 不同模型的检测结果评价指标

模型经两类数据集训练后在测试集上的病害检测结果如图7。其中,虚线框与实线框分别为采用匀质图谱与二相介质图谱在实测图谱上裂缝与层间不连续的检测结果,框内数字表示框内含有病害回波的概率,即置信度。

图7 基于两类数据集训练模型后的检测结果Fig. 7 Detection results after training models based on two types of datasets

图7(a)为层间裂缝在原始雷达图谱上的回波特征,两类数据集对裂缝顶部回波的识别效果较好,预测框内置信度分别为0.92与0.93。采用数据集1# 进行训练后未能检测出裂缝底端的回波特征,而采用数据集2# 训练后裂缝双曲线组均可被有效检测,但预测框内的置信度不高。这是由于图谱未经过信号预处理,病害回波信号的深度特征不显著,网络特征提取结构的学习能力有限。

图7(b)与图7(c)分别表示原始雷达图谱在经过预处理后的裂缝回波特征。当雷达图谱经过预处理后,病害回波特征与路面完好区域差异显著,预测框内的置信度明显提高,裂缝底端回波特征在匀质图谱的训练集中也能被有效辨识,说明对图谱进行预处理后可以提高网络的检测准确性。

图7(d)为连续裂缝在剖面图上的回波特征。对于裂缝回波双曲线顶端灰度增强、两翼绕射的显著特征,模型均可准确识别,而对于部分波形特征缺失的裂缝回波,采用匀质图谱训练无法有效辨识。匀质图谱中雷达波不会产生随机散射,裂缝回波双曲线较缓,顶部均匀无起伏。在实测图谱上,当裂缝为贯穿裂缝时,其双曲线顶部在穿过层位分界面时会发生中断,这与匀质图谱中的特征存在差异,导致识别效果不佳。

图7(e)为原始雷达图谱中层间不连续形成的异常回波区域。采用两类数据集进行训练后的模型均能有效识别,预测框内的置信度分别为0.93与0.95。由于层间不连续回波表现为突然出现的层位同相轴,或均匀同相轴灰度显著增亮,故较裂缝更易识别。图7(f)同时存在裂缝与层间不连续两类病害,二相介质图谱训练模型对于层间不连续的检测区域更为精确,并能检测出下层裂缝的回波特征,采用匀质图谱训练模型仅能识别出层间不连续回波特征,且检测区域范围不精确。

图7(g)中层间不连续回波左侧存在两处裂缝与不连续病害的相似波,两类数据集训练模型均未发生误判,说明网络具有较好的稳定性。图7(h)、图7(i)、图7(j)分别表示一定程度缩小或放大剖面图中病害特征的检测结果。可见,放大异常区域后检测置信度有所增加,且用匀质图谱训练模型在缩放图谱上将层间不连续误判为裂缝,这表明对输入图像进行增强处理可能会提高网络提取图谱特征的能力,但也可能会造成误判。

综合图7中两类数据集在YOLO v5模型训练后的测试结果可知,道路结构内部存在连续开裂,采用二相介质图谱训练模型的检测精度较高,适度的图像预处理(如增益)可提高模型识别病害回波的准确性,数据增强处理(如裁剪过小)可能会导致波形特征缺少而造成模型误判。两类数据集训练模型均可准确识别层间不连续导致的异常回波特征,在图谱中同时存在裂缝、层间不连续与两类病害回波的相似波时,采用二相介质图谱训练模型能精准识别两类病害且不会误判,证明二相介质图谱训练模型较匀质图谱训练更具准确性与稳定性。

5 结 论

1)结构裂缝在实测图谱中的回波特征,表现为上下平行的多个开口向下双曲线组,两翼开口较窄,顶部振幅较强,穿过层位回波同相轴时有间断;层间不连续回波表现为梯形同相轴,振幅较强,两端绕射不显著。

2)匀质模型中裂缝回波双曲线组之间无反射,信号幅值随裂缝长度增加而增强;层间不连续同相轴随长度发展逐渐呈梯形状。

3)雷达波在“沥青-集料”二相介质中会发生小尺度的随机散射,导致波面不平滑、波形模糊不清,雷达波在均匀介质中不会受到散射,波面保持平滑,波形无畸变。因此,采用二相介质获取的仿真图谱较传统匀质模型更符合实测图谱的病害回波特征。

4)采用二相介质图谱训练模型后在测试集上的mAP@0.5为96.33%,F1分数为0.938,两项指标均大于采用匀质图谱训练模型后的检测结果,表明采用二相介质图谱进行训练可提高网络检测的精度。采用YOLO v5模型检测雷达图谱较其他深度学习模型的浮点操作最少,表明模型具有一定的优越性。