基于圆锥微凸体的结合面法向刚度改进模型*

李 勇,兰国生,杨 琦,冀成龙,宋建国,刘宇龙

(太原科技大学机械工程学院,太原 030024)

0 引言

机床由许多零部件及其相互连接的结合面组成,结合面在机床运行过程中起着传递运动、载荷和能量的重要作用。机床各机械接触面间的刚度占机床总刚度的60%～80%,所产生的变形量占机床总变形量的85%～90%[1-2]。因此,对粗糙结合面间的接触力学性能的研究对于提升机械系统整体性能有重要意义。为此,国内外学者对结合面间的接触特性进行了大量的研究。

对于结合面接触特性的研究,GREENWOOD等[3]提出了经典的“G-W接触模型”,但该理论模型仅考虑弹性变形阶段,且假设条件比较苛刻,适用性小。CHANG等[4-6]同时考虑了微凸体弹性和塑性两个阶段,结合塑性变形体积不变原理,得到了塑性变形阶段实际接触面积,建立了结合面接触刚度模型,但是该模型在弹塑性临界处出现了接触载荷的不连续。JENG[7]将粗糙表面微凸体等效成椭圆形微凸体,建立了结合面法向接触载荷统计学模型。许志倩等[8]将粗糙表面等效成圆锥微凸体,采用随机抽样的方法计算得到符合正态分布的结合面微观形貌,建立了结合面三维接触力学模型;田红亮等[9]同样将表面微凸体等效成圆锥形,通过对反双曲余弦应力定积分,计算得到弹性与塑性阶段的接触力。但以上模型均基于统计学原理,取样长度和粗糙表面统计参数的获取都受制于试验测试仪器的分辨率[10],不具有客观唯一性。

BHUSHAN等[11]基于分形几何理论,建立了粗糙结合面接触分形模型,即M-B模型,该模型具有尺度独立性和客观唯一性。YAN等[12]将二维轮廓曲线扩展到三维轮廓曲线,采用三维分形几何方法建立了结合面弹塑性法向接触刚度模型。张学良等[13-14]基于分形理论和M-B模型,首次得到粗糙表面法向刚度的分形模型,分析了各个参数对结合面接触特性的影响规律。兰国生等[15]将粗糙表面微凸体等效成圆锥形微凸体,计算了微凸体弹性与塑性变形阶段的接触特性,建立了结合面法向刚度分形模型。王润琼等[16]基于分形几何理论,引入域扩展因子对接触面积分布的影响,并考虑到微凸体间的相互作用,建立了机械结合面接触刚度分形模型。

但是以上都是基于球形或椭圆形微凸体研究接触特性,并未考虑圆锥形微凸体情况,或者模型使用的微凸体接触面半径为理论接触半径,与实际接触半径差别较大,影响模型准确性。因此,本文将粗糙结合面等效为圆锥形微凸体,对接触半径值进行了修正,引入域扩展因子影响的微接触横截面积分布函数,建立了基于圆锥微凸体的结合面法向接触刚度改进模型,并进行模拟仿真,分析了相关形貌参数对接触特性的影响,并对仿真结果进行了讨论,最后对比真实试验所得数据发现,本文模型更接近真实数据,验证了模型的有效性,可作为理论计算模型。

1 结合面形貌特征

YAN等[12]改进了传统的W-M函数,改进后的W-M函数能够更好地等效具有分形几何特征的三维各向异性粗糙表面,即:

(1)

运用此模型模拟粗糙表面形貌特征时,z代表微凸体高度,L代表采样长度,D代表粗糙表面分形维数(21,一般取值1.5),M代表模拟表面凸起数目,n代表频率指数,指数上限nmax=int(logγ(L/Ls)),Nm,n代表随机相位。

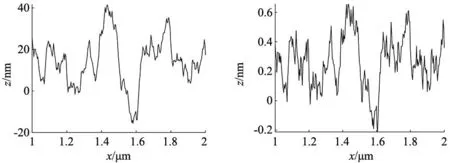
对上述函数进行模拟仿真,设定参数L=0.57 μm,M=10,γ=1.5,D=2.2/2.5/2.8,G=1.59×10-7μm,图1为模拟的三维表面形貌,图2为垂直于y轴的平面与仿真图像所截取的在xoz平面内的二维粗糙表面轮廓曲线。

图1 W-M函数模拟的粗糙 表面三维形貌(D=2.5)

(a) D=2.2 (b) D=2.5

从图2可以看出,其他参数一致时,分形维数越大,二维图像波峰波谷越密集,即粗糙表面微凸体数目越多,且微凸体越“尖锐”。

当M=1,m=1,W-M函数将退化为:

(2)

2 单个微凸体法向接触模型

工程中相互接触的两粗糙平面可以等效成为一刚性平面和一粗糙表面接触,如图3所示。

图3 粗糙表面与刚性平面接触

接触过程中粗糙表面微凸体变形量可由式(2)对应的余弦函数波峰与波谷之差表示,即:

(3)

以往的研究用改进的W-M函数余弦波来等效球形微凸体,微凸体曲率半径对应余弦波的曲率半径,但真实粗糙表面形貌是复杂的,粗糙表面微凸体存在多种形态。为了扩展结合面接触特性模型的适用范围,本文可将接触表面微凸体等效成为圆锥形微凸体,与刚性平面接触变形如图4所示。

图4 等效圆锥微凸体与刚性平面接触

图4将余弦波顶点与接触表面两边缘点相连,做等腰三角形,此等腰三角形绕竖直轴旋转得到的即为等效圆锥微凸体,其中ω为微凸体法向变形量,r′为微凸体名义接触半径,r为微凸体真实接触半径,由文献[17]分析计算出接触过程中微凸体真实接触半径r与名义接触半径r′的关系:

(4)

将式(4)带入式(3)中得,微凸体实际变形量为:

(5)

圆锥半顶角的余切值为:

(6)

2.1 圆锥微凸体弹性接触状态

由文献[18]可以得到结合面接触过程中弹性变形阶段的微凸体法向接触载荷pe表达式为:

pe=0.2Ecot(β)a

(7)

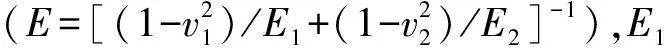
平均接触载荷为:

pea=0.2Ecot(β)

(8)

根据刚度定义,联立式(5)～式(7)可得,等效圆锥形微凸体弹性变形状态下的法向刚度表达式为:

(9)

2.2 圆锥微凸体塑性接触状态

微凸体临界弹性变形量表示为ωc,当变形量超出这一值时,微凸体进入塑性变形阶段,圆锥微凸体法向接触载荷pe和接触面积a之间的关系为:

pp=Ha

(10)

平均接触载荷为:

ppa=H

(11)

2.3 微凸体弹性与塑性临界

为了使接触载荷模型在弹塑性变形临界处光滑连续,令弹性和塑性阶段临界的平均接触载荷相等,即:

(12)

得圆锥形微凸体变形临界接触面积为:

(13)

式中:k=H/σy为材料硬度系数,k一般取2.8;σy为较软材料的屈服强度,φ为材料塑性指数。

对式(13)进行模拟仿真,分析参数D、G、φ与微凸体临界接触面积ac的关系,选取粗糙结合面参数值:D=2.1～2.9,G=10-13～10-9,φ=0.7～2.5,仿真结果如图5～图7所示。

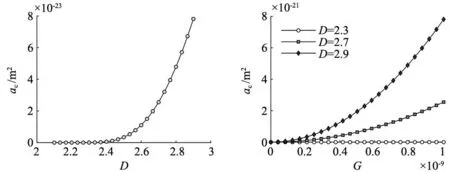
图5 D对ac的影响曲线(G=10-10,φ=1.5)

图7 φ对ac的影响曲线(D=2.7,G=10-9)

由图5～图7可知,等效圆锥微凸体ac随着D的增大而增大,并且在D>2.6之后增长速度加快,且随着G的增大而增大,随着φ的增大而减小。同时,临界接触面积增加,导致相同接触面积内微凸体弹性变形占比减小。

3 结合面法向接触刚度建模

文献[19]优化了结合面微接触横截面积分布函数,考虑域扩展因子的影响,给出了更符合实际的微接触横截面积分布函数,即:

(14)

式中:a表示结合面上微凸体接触面积,al表示参与接触的表面微凸体中最大微凸体接触面积,φ表示微凸体接触面积分布域扩展因子(φ<1),可通过式(15)计算得出:

(15)

对式(14)进行模拟仿真,分析参数D与na的关系,选取粗糙结合面参数值:D=2.1～2.9,al=10-10,a=10-15,仿真结果如图8所示。

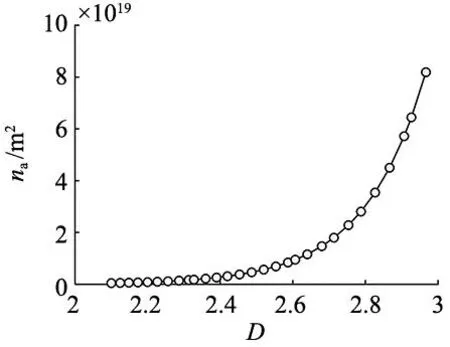
图8 D对na的影响曲线(G=10-10,al=10-10 m2,a=10-15 m2)

由图8可知,当分形维数增大时,结合面接触面积分布密度函数随之增大,即相同接触面积内处于接触状态的圆锥微凸体数量增加,与图2所呈现的情况相符,且分形维数处于2.6～3之间,临界接触面积增长速度加快。

结合面总实际接触面积为:

(16)

即:

(17)

结合面总法向接触载荷为:

(18)

将式(7)、式(10)、式(13)、式(14)及式(17)代入式(18),得:

(19)

结合面总法向接触刚度为:

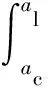
(20)

将式(7)、式(13)、式(14)和式(17)代入式(20),得:

(21)

将式(19)和式(21)进行无量纲化处理得:

(22)

(23)

4 结合面接触模型仿真以及试验对比

4.1 模型仿真

(a) D=2.3 (b) D=2.5

(a) D=2.3 (b) D=2.5

(a) D=2.3 (b) D=2.5

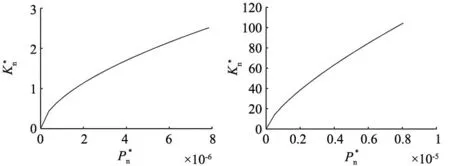
(a) D=2.1 (b) D=2.2

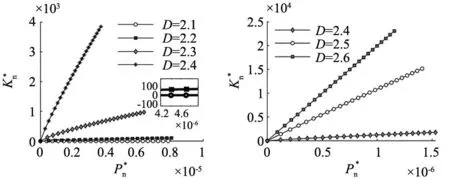
(a) D=2.1～2.4 (b) D=2.4～2.6

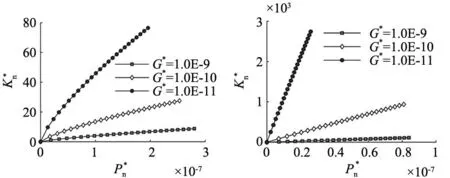
(a) D=2.3 (b) D=2.5

(a) D=2.3 (b) D=2.5

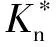
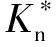
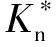
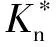
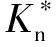
4.2 试验验证

为验证本文所建立模型的有效性,采用文献[21]与文献[22]测得的试验数据与本文模型理论值进行对比,间接验证本文模型的有效性。试验方法是从宏观来直接获得结合面法向接触特性的方式,并且可以与从微观角度进行建模计算得到的理论模型进行对比,从而验证本文模型有效性。

文献[21]试验原理及方法:沿垂直方向向上下两试件组成的结合面系统分级施加法向载荷,并通过与其相连的涡流位移传感器和压力传感器(静态、动态力传感器)对法向相对位移和法向面压进行测量,并通过一定的理论计算得到法向静刚度与法向变形量或法向面压之间的关系。具体做法为:运用逐级法向加载的形式,从监测设备中得到相应法向载荷值和结合面相对位移平均值,从中扣除试件的压缩变形影响量,得到结合面接触变形量,再计算结合面法向接触面压。接着,对所获得的有效法向相对位移和法向面压进行函数拟合,得到粗糙接触面法向静刚度关于法向变形量表达式。再对两接触面施加法向动态激励,根据试验装置建立结合面动态力学模型,最后得到粗糙接触面法向动态接触刚度。

文献[22]试验原理及方法:与文献[21]相似,通过试验装置向所测两试件施加法向外载荷和外部激励,所连接的相应传感器将所测得的压力、位移信号转换成数字信号,再计算模拟确定粗糙接触面的动力学特性。具体做法为:先使用螺栓对待测两试件施加静态预紧力,再通过冲击锤对试件施加外部动态激励。应用多点激励的方法,从固定在下部件的三轴加速度传感器得到对应的响应信号,并进行模拟测试得到两试件接触面之间的动力学性能。

文献[21]中上下试件材料为45钢,材料相关属性参数为:硬度H=1960 MPa,弹性模量E1=E2=207 GPa,泊松比v1=v2=0.29,文献[22]中上下试件材料为铸铁,材料相关属性参数为:硬度H=220 MPa,弹性模量E1=E2=130 GPa,泊松比v1=v2=0.25,两试验中上下两试件加工方式均为铣削加工。通过铣削加工方式得到的粗糙表面分形参数如表1所示,这些参数通过文献[23]中的结构函数法得到,表2为两试件粗糙表面接触的等效分形参数值。

表1 铣削加工试件表面分形参数

表2 试验试件接触表面等效分形参数

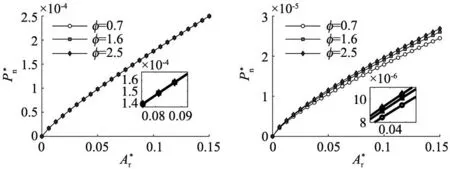
图16和图17为理论模型与试验数据的对比,试验数据由文献[21]与文献[22]中获取,并与文献[15]的模型与文献[24]的模型进行对比,本文模型将粗糙表面微凸体等效成为圆锥形微凸体,李小鹏模型将粗糙表面微凸体等效成为球形微凸体,孙万模型也等效为圆锥形微凸体,但使用的微凸体接触半径非实际接触半径。

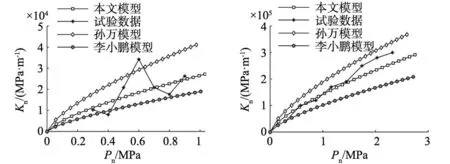
图16 不同模型与文献[21]试验数据对比

由图16和图17可知,本文所建的圆锥形等效微凸体结合面接触刚度模型与真实试验值的变化趋势一致,都随无量纲法向接触载荷的增大而增大,且相较文献[15]的模型和文献[24]的模型与试验结果更为接近,精度有了一定的提高,并且在变形临界状态连续且光滑。因此,将粗糙接触表面微凸体等效成圆锥形微凸体具有可行性。

误差分析:由于真实工况中两粗糙接触表面间往往存在一定的液体介质,与固-固接触共同产生整个结合面的刚度,本文忽略了液体介质刚度;本文只考虑了微凸体在弹性和塑性两个阶段的接触变形情况,未考虑弹塑性阶段;本文忽略了微凸体间的相互作用对实际微凸体变形量产生的影响,因此导致理论模型结果与真实试验值有一定的偏离。

5 结论

对于由等效圆锥形微凸体组成的结合面,当分形维数增大时,无量纲法向接触刚度先增大后减小,且临界点处于2.6左右;当分形粗糙度参数增大时,无量纲法向接触刚度随之减小;当塑性指数增大时,无量纲法向接触刚度随之增大。

通过仿真研究更进一步发现,粗糙结合面无量纲真实接触面积越大,结合面无量纲法向接触刚度越大。当粗糙结合面无量纲真实接触面积一定时,影响结合面法向接触刚度的主要因素包括微凸体临界接触面积和结合面接触面积分布密度函数两种,微凸体临界接触面积增大,处于弹性接触状态的微凸体数目比例减小,接触刚度随之减小;结合面接触面积分布密度函数值增大,发生接触变形的微凸体数量增大,接触刚度随之增大。

本文所建模型与试验值更加接近且趋势相同,证明了本文模型的正确性和有效性,为未来机械结构结合面接触特性方面的研究提供了参考。对于今后进一步的研究,可以将微凸体接触变形扩展到弹塑性变形阶段,或考虑润滑介质刚度的影响,使得理论模型预测值更准确。