基于形变场灰度场插值网络的切片间超分辨率

刘 迅，张 东，袁达龙

（武汉大学物理科学与技术学院，湖北 武汉 430072）

0 引 言

磁共振成像（MRI）是一种医学成像技术，被广泛应用于临床的医学诊断，它对于癌症的早期识别和诊断至关重要［1］。由于传统的三维成像通常会导致较长的扫描时间，大多数医院都采用二维多层切片成像。MR 图像切片的厚度是由硬件限制和脉冲序列时序决定的［2］，二维切片通常相对较厚，这导致了切片间的分辨率较低，使冠状位和矢状位的图像有明显的锯齿状和阶梯状边缘，对组织分割、可视化和疾病诊断产生负面影响［3］。因此，提高MR 图像切片间分辨率对于病变区域的可视化和早期诊断十分重要。

目前有很多方式实现切片间超分辨率任务［4-15］，一种方式是从不同切片方向的各向异性多层MR 图像中重建高分辨率各向同性图像。Poot 等［16］提出了一种重建高分辨率图像的方法，该重建方法利用了一个改进的MR 图像的采集模型，得到了一个具有线性方程的系统，再利用共轭梯度法和该线性系统，从物体的MR 图像中重建出一个高分辨率的图像。另一种方式是通过高分辨率和低分辨率图像对来完成超分辨率任务，Pham 等［17］受到SRCNN 的启发，提出了一种3D SRCNN 模型，提高了MR 图像的分辨率，通过对卷积神经网络（Convolutional Neural Network，CNN）架构［18］的优化，提升了PSNR 值。Liu等［19］提出了一种边缘增强超分辨率生成对抗网络（EE-SRGAN）。该方法采用2 级超分辨率生成网络来解决MRI 单方向分辨率降采样比达到12 倍的问题，此外，为了克服高峰值信噪比引起的图像平滑性问题，构建了一个基于TSSR的生成对抗网络，以实现更多的图像细节。本文方法首先根据VoxelMorph［20］的方法利用低分辨率图像中一对相邻的切片进行无监督训练。因为在训练的过程中没有提供真实的形变场和高分辨率图像，所以训练过程可以看作是无监督的。与监督学习模型相比，无监督学习不需要人工标注的数据，所以不受标签中可能存在的错误或偏差的影响。训练完成之后，网络就可以根据2 张相邻切片估计出两者之间的双向形变场，形变场可以表示出相邻2 张切片之间的像素点对应关系，利用双向形变场就可以估计切片之间任意网格点位置的中间形变场。因为2 张相邻的切片之间不仅仅有像素点的位移，还有较小的灰度值变化，所以本文算法引入了灰度场，以便得到更精确的结果。利用中间形变场和灰度场完成中间切片的插值，从而提高切片间超分辨率。

1 方 法

1.1 算法流程

针对MR 图像切片间的分辨率与切片内的分辨率具有较大差异的问题，本文提出一种基于形变场和灰度场插值网络的切片间超分辨率的算法。图1 为本文的算法流程，整体算法流程可以分为3 个步骤：1）数据准备，包含数据集的划分和数据预处理；2）搭建网络框架；3）投入测试集，并分析预测结果。

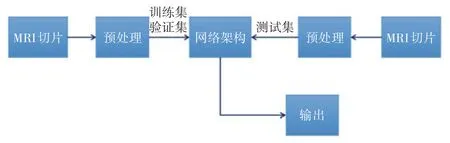
图1 算法流程

1.2 网络结构

本文算法模型的网络架构如图2 所示。先将移动图像和固定图像堆叠起来，输入第一个网络，利用网络输出一个形变场，然后将移动图像和形变场通过空间变换生成形变后的图像，再将形变图像和固定图像堆叠输入第二个网络，网络输出一个灰度场。训练时，网络先训练得到形变场，第一个网络参数θ通过最小化形变图像和固定图像之间的差异来更新。然后固定第一个网络的参数，再训练灰度场，最后利用形变场和灰度场对图像做变换，得到最终的图像。第二个网络参数θ通过最小化最终图像和固定图像之间的差异来更新。

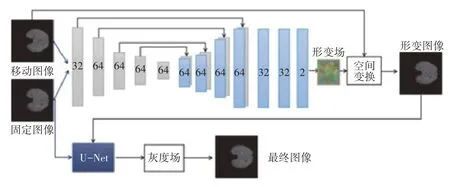
图2 网络架构图

生成形变场的网络是近似于U-Net 的编解码结构［21］。使用卷积将每一层的空间维度减小到一半。在解码阶段，交替进行上采样、卷积和跳跃连接，这些连接将在编码阶段学习到的特征直接传播到生成配准的层中。在训练中，将移动图像和固定图像输入网络，因此第一个网络的输入大小为240×240×2，编码器和解码器阶段都使用的二维卷积层的卷积核大小为3，步长为2，Leaky ReLU 层［22］的参数为0.2，网络的输出（即形变场）大小为240×240×2。生成灰度场的网络也类似，第二个网络的输入的大小为240×240×2，网络的输出（即灰度场）大小为240×240×1。

1.3 插值方法

传统的插值方式有最近邻插值［23］、线性插值［24］等，但是获取2 张切片的中间切片不能简单地使用传统插值。这种插值产生的中间图像比较模糊，因为没有考虑图像位置变化，所以应该寻找2 张切片之间的点对应性，也就是要找到移动图像上的每个像素点在固定图像上对应的位置。这个对应关系表明了切片间的坐标由移动图像变为固定图像时像素点的移动轨迹，因此也可以推断出像素点的相应坐标。

设定2 个输入图像I0和I1和一个中间位置t∈（0，1），本文的目标是预测位置为t的中间图像。配准场ϕ可以分解为一个恒等变换和一个位移场，即ϕ=Id+u，其中Id 是恒等变换，u表示位移场。假设ϕt→0和ϕt→1分别表示从It到I0和It到I1的配准场，Gt→0和Gt→1分别表示从It到I0和It到I1的灰度场。得到了配准场和灰度场之后，合成中间图像可表示为：

其中，f（·，·）是一个使用双线性插值的反向变换函数，参数α0用来控制给定的2 张切片图像I0和I1对新合成图像的贡献的权重。与一般插值方法中的设计类似，新合成的图像所处位置t越靠近0，I0的贡献权重α0越大，越靠近1，I1的贡献权重1-α0越大。因为中间图像未知，所以配准场ϕt→0和ϕt→1无法计算。为了解决这个问题，本文利用2 个输入图像之间的ϕ0→1和ϕ1→0来合成中间的ϕt→0和ϕt→1，ϕt→0和ϕt→1的计算公式如下：

或：

或：

再通过双向配准场来得到中间的近似配准场，如式（6）和式（7）：

在得到近似配准场和之后，可以得到t位置的切片，如式（8）：

1.4 损失函数

本文选择的损失函数是相似度损失、平滑度损失以及均方误差损失［25］。相似度损失可以用来衡量图像之间的相似性，本文选择的相似度损失是互相关损失［26］。最小化相似度损失可以使预测的切片更接近真实的切片，但是可能产生一个不连续的形变场，因此需要加入一个平滑度损失用来约束形变场，其中λ取1。具体表达式如式（9）所示：

设ϕ为将I0的坐标映射到I1的坐标的配准场。I0◦ϕ表示将I0通过ϕ形变所得到的结果，令I0◦ϕ为，令(p)表示图像上n×n个像素的平均灰度值，即其中pi表示p周围的n×n个像素点，在本文实验中该值设置为9，由于CC 的值越大，代表图像配准效果越好，因此可以取Lsim（I0，I1，ϕ）=1-CC（I1，I0◦ϕ），如式（10）所示。利用相邻体素之间的差异来实现近似的空间梯度，平滑度损失如式（11）和式（12）所示：

公式（13）的损失函数由均方误差损失和平滑度损失组成，均方误差损失使预测的中间切片更接近真实切片，平滑度损失可以约束灰度场，提高图像的准确性。

2 实验与结果分析

2.1 实验数据

本文选择BraTs2018 数据集作为实验数据集，该数据集一共有285 个病例，每个病例有t1、t1ce、t2、flair这4个模态的磁共振图像。且每个的图像大小均为240×240×155，其间距为1 mm×1 mm×1 mm。本文从切片选择方向上的第一张切片开始，每8 张切片选择一张，制作出低分辨率图像，即间距为1 mm×1 mm×8 mm的低分辨率序列，再将实验数据集按7：1：2拆分成训练集，验证集和测试集，并将所有切片数据作归一化。所有网络的优化过程使用Adam 优化器，学习率为0.001，平滑常数分别为0.5 和0.99。每次训练批次大小为16，最大迭代轮次为1000。

2.2 评价指标

为了客观评价采用本文算法所插值出来的切片是否接近真实的切片，本文采用了2个指标：

1）峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）：这是一种评价图像的客观标准，可以用来评价原图和插值后图像是否相近。其计算公式为：

2）结构相似度（Structural Similarity Index Measure，SSIM）：这是一种衡量2 幅图像相似度的指标［27］。其计算公式为：

其中，n是图像的位数，这里为16，x是真实的切片图像，y是预测的切片图像，N是图像的有效点数，μ是平均灰度值，σ表示方差，σxy表示2 图像的方差，c1、c2均为常数，PSNR 和SSIM 的值越高，表示预测的切片图像和真实切片图像越相似。

2.3 实验结果与分析

为了定量评估本文算法的性能，通过从MR 序列中选取切片选择方向上中间的2 个切片作为0 号和1号切片。本文算法实现了8 倍的超分辨率，分别在2张切片之间的1/8、1/4、3/8、1/2、5/8、3/4 和7/8 处插值了7 张中间切片。本文将原来的2 张切片与1/4、1/2和3/4 处位置的切片进行比较，以显示插值切片的效果。图3 显示MR 图像各个模态的插值结果，其中图3（a）～图3（d）分别为测试集上的t1、t1ce、t2、flair 模态的低分辨率MR 图像的2 张相邻切片的插值结果，第1 列和第5 列分别为测试集中所选取的2 张相邻切片，中间3 张切片为利用形变场和灰度场进行插值得到的结果，其中红框的位置表示一些切片出现明显变化的区域。如图3所示，每2张切片的变化相对连续，算法的效果较好。

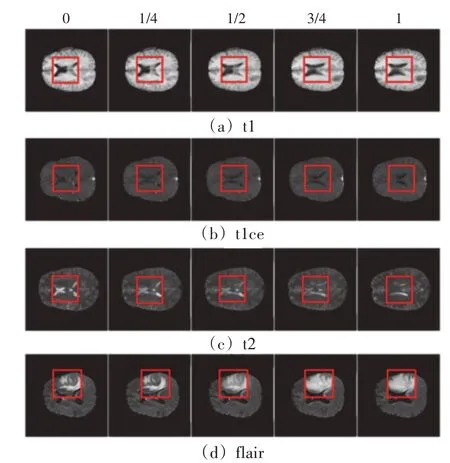
图3 MR图像切片间超分辨率结果

将测试集中低分辨率MR 图像的相邻切片逐一输入网络，得到所有插值切片后，按输入顺序将所有切片合并为高分辨率MR 图像。 由于不同模态的结果相对类似，从t1ce 和t2 这2 个模态的超分辨率结果中选取了3 个方向剖面显示出来，其结果如图4 和图5 所示。其中图4 为t1ce 模态的结果，图5 为t2 模态的结果。从图中可以看出本文算法所得到的图片明显比最近邻插值和双线性插值算法得到的图片更加清晰，边缘更加平滑，更加接近真实的图像。同时，加入灰度场后的图像比不加灰度场的图像更加清晰。

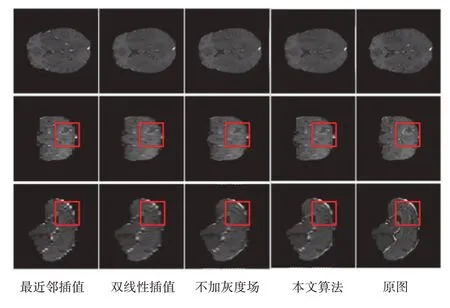
图4 t1ce模态3个方向的对比图

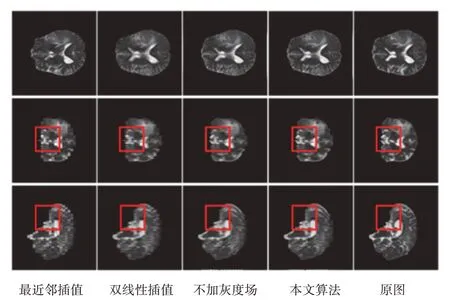
图5 t2模态3个方向的对比图

除了可视化的结果之外，本文分别计算了3 种方法得到的结果相较于真实图像的PSNR 和SSIM，其结果如表1 和表2 所示。在实现超分辨率的任务上，可以看到本文算法在对比最近邻插值和线性插值的算法上，结构相似度的数值相近，而峰值信噪比则有明显提升。通过对比是否加入灰度的插值结果，可以看出引入灰度场对PSNR和SSIM均有一定的提升。

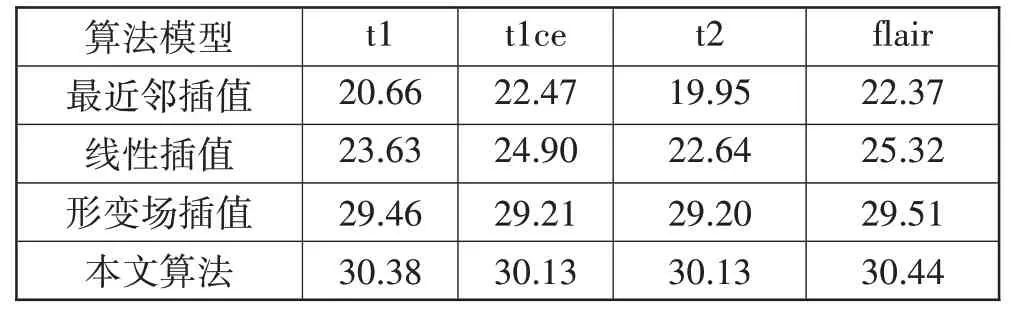
表1 PSNR的统计结果

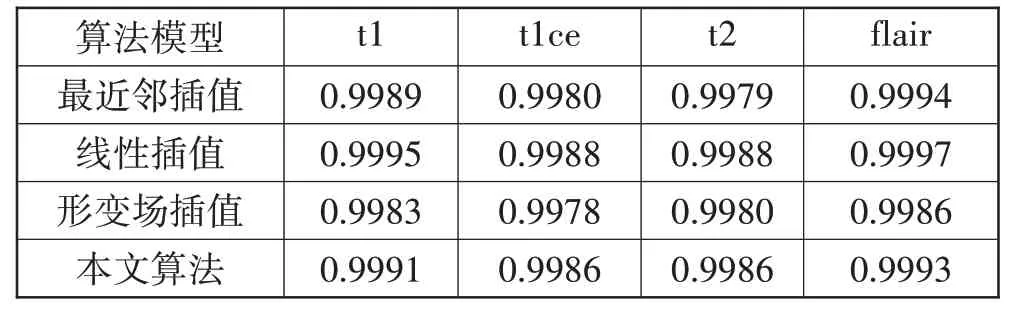
表2 SSIM的统计结果

本文第一个网络的参数量（Params）为0.4366×106，计算量（FLOPS）为108.424 GB，第二个网络的参数量为0.4363×106，计算量为108.158 GB。

模型的参数量比较小，意味着模型可以在较小规模的内存中存储。计算量主要反映模型在推理或训练过程中的计算开销。模型的计算量越大，意味着模型需要越长的计算时间。

3 结束语

本文提出了一种基于形变场和灰度场插值网络的切片间超分辨率，解决了临床上MR 图像切片选择方向上分辨率远低于切片内分辨率的问题，有助于医生做出更加准确的临床诊断。在实验数据集上，本文选用了多模态脑肿瘤分割挑战（BraTs2018）数据集。在网络算法上，引入了灰度场，并且进一步设计了基于形变场和灰度场的插值算法。实验结果表明，本文算法在不需要任何额外数据的情况下能够很好地完成切片间超分辨率，可以用于改善多切片MR 图像切片厚度大导致的切片间分辨率过低的问题。