基于共同邻居数的重要节点发现算法

盛家烨

（哈尔滨工业大学建筑学院互动媒体设计与服务创新文化和旅游部重点实验室，黑龙江 哈尔滨 150001）

1 重要节点发现

近年来，复杂网络作为工具被广泛地用于研究存在于自然界和人类社会的各个领域的传播现象，例如流行病在社会联系网络中传播［1］、病毒在通信网络中传播［2］、谣言和信息在社交网络中传播［3］等。作为复杂网络中的基本组成部分，节点在传播过程中发挥着不可忽视的作用。因此，识别网络中的重要节点是促进或抑制传播的一个有效手段。

目前，已经有大量用于识别重要节点的算法被提出，如度中心性（DC）、接近中心性（CC）、Katz中心性、介数中心性（BC）、LocalRank［4］、K-shell 算法［5］、PageRank［6］等。这些重要节点发现算法可以分为3 类：基于网络结构的中心性算法、基于迭代的中心性算法和贪婪算法。

基于网络结构的中心性算法普遍从节点的邻居信息中识别该节点的重要性。度中心性简单地认为一个节点的邻居数越多，影响力越大，不足之处在于仅考虑了节点最局部的信息，因此实际表现并不理想。针对这一问题，一个改进方向是考虑更多的、更高阶的邻居信息。如LocalRank［4］就考虑了节点共4阶的邻居信息；CI［7］被广泛地认为是一种识别重要节点的优秀中心性指标之一，它通过节点的余度和节点第l阶邻居的余度之和来计算该节点的重要性。

此外，考虑到复杂网络中的边本身就是对节点之间相互关系的抽象，因此通过网络中的路径来计算节点的重要性是另一条路线。例如介数中心性的核心是节点对之间的最短路径，它认为通过某节点的最短路径数越多，则这个节点的重要性也就越高。但是在现代网络上运行的许多应用程序需要以几乎实时的方式计算中介中心性，必须处理大量节点和边。而中介中心性高昂的时间复杂度导致这几乎无法实现。针对这一问题，Bonchi等［8］选择通过近似的方式来计算中介中心性；Fan 等［9］考虑到大部分应用场景只需要top-k 的节点，基于图神经网络在小规模网络上训练出了模型，能够为任何未见过的网络的节点分配相对BC分数，从而识别出高介数中心性节点。

另一类基于网络结构的中心性算法利用节点的位置信息来识别该节点的重要性。K-shell 算法通过迭代地剥去网络外围的节点（度最小）来获取节点的位置信息，并认为节点的位置越处于网络核心，则节点越重要，传播能力越强。然而K-shell 算法也有其不足，例如划分粒度太粗，会给大量节点分配相同的K-shell 值［10］。因此，有不少算法针对这个问题进行了改进［10-11］。

基于迭代的中心性算法考虑了节点间的相互增强效应，在迭代的过程中不断优化节点的重要性。这类经典算法除了PageRank 外，还包括HITs［12］和LeaderRank［13］等。事实上，尽管不同方法的具体实现细节不同，但都遵循着一个基本思想：节点的重要性取决于指向它的其他节点的数量和质量。例如，以PageRank及其改进［14-15］为代表的一类方法，通过迭代来模拟随机游走的过程，并假设节点的邻居越重要，其本身重要性也越高。这类算法适用于有向网络，面对无向网络时表现不佳［16］。

贪婪算法的目标是在寻找种子节点的过程中，保证种子集的每一次增加都可以使影响力的增量最大化［17］。例如Kempe等［18］用蒙特卡洛模拟法反复选择产生最大边际影响力增量的节点作为种子集。显然，贪婪算法的每一次搜索都需要对每一个节点重新计算一遍影响，因此时间复杂度极高。针对这一问题，Mugisha 等［19］通过迭代基于置信度传播设计的自洽方程，一次性计算出所有节点的影响，提出了BPD 算法；Li［20］提出了BPD 在因子图上的扩展形式；而CoreHD 算法［21］则是另辟蹊径，启发式地不断删除网络2 核中度最大的节点，免于为每个节点计算删除后的影响。尽管如此，贪婪算法的时间复杂度依然过高，以至于无法运用到大规模网络上。

近年来，有一种混合中心性方法作为中心性方法的改进，在多维视角下量化节点的传播影响力［22-23］。这类算法从不同的角度将各类网络中节点的局部指数、半局部指数和全局指数结合。如Li 等［24］基于节点的K-shell 值，将一个节点的邻居分成4 类，并加以不同的权重。Sheng 等［25］使用共同邻居数来衡量节点与邻居之间信息共享的紧密程度，并依此对邻居区分。Mo 等［26］基于证据理论考虑了现有的度中心性、介数中心性、效率中心性和相关中心性，然而，如何选择维度指数，在准确性和简单性之间达到一个很好的平衡，仍是一个挑战。

总之，现有的算法很难在准确性和简单性之间达到平衡。有些算法表现得非常简单，但限制了准确性，如DC 和K-shell 分解算法，而其他具有高准确性的算法无法应用于大规模网络，如BC 和贪婪算法。基于邻居信息的算法为解决上述问题提供了一个很好的思路。虽然现有的算法已经全面考虑了邻居的顺序、位置和重要性，但仍然没有对邻居在传播中的作用进行具体描述，也没有区分邻居在不同维度上的贡献。

本文提出一种新的算法来识别重要节点。该算法从2 个方面对邻居在传播中的贡献进行了分类：1）加强了节点所在的紧密连接的局部区域的传播效果；2）通过邻居将信息扩展到网络的其他区域。本文提出的算法的排名是通过结合共同邻居的数量和节点的K-shell 值产生的。在8 个基于标准SIR 模型的真实网络上模拟了传播过程。实验结果表明，本文提出的算法比其他广泛使用的算法表现得更好，而且计算复杂度更低。

2 方 法

任何传播过程总是从几个初始种子节点开始。种子节点将信息或病毒传播给其邻居。邻居节点被激活后，再进一步传播给邻居的邻居。显然，节点的邻居是其传播能力的重要组成部分。因此，若能明白节点的邻居在传播过程中扮演着什么角色，就能更加有效地识别出网络中的超级传播者。基于这一思想，本文提出一个基于节点邻居信息，称之为Semi-local Centrality based on Common Neighbors（SCCN）的重要节点发现算法。

本文算法受到了PageRank（PR）算法的启发。PageRank 算法认为万维网中一个页面的重要性取决于指向它的其他页面的数量和质量，如果一个页面被很多高质量页面指向，则这个页面的质量也高。初始时刻，赋予每个节点相同的PR 值，然后进行迭代，每一步把每个节点当前的PR值平分给它所指向的所有节点。每个节点的新PR值为它所获得的PR值之和，于是得到节点i在时刻t的PR值为：

式中，代表指向节点i的节点集合；代表节点j的出度之和；N代表网络中所有节点的数量；c代表随机跳转概率，防止出现出度为0 的节点不断吸收PR值的情况。PageRank 算法实际上是马尔科夫链上随机游走过程，模拟了用户浏览网页的动态过程。虽然PageRank 并没有明确邻居节点的具体作用，但是其考虑传播动态过程的思路是值得借鉴的。因此，SCCN 算法在探究邻居节点的贡献时，考虑了传播本身的动态特点。

假设存在一个具有N个节点与M条边的网络G。对任意一个节点i，Γi代表节点i的最近邻居集合。当节点i 被激活时，它会以概率β尝试去激活每一个邻居节点。

首先，如果节点i存在邻居节点j和k，且j激活成功，k激活失败。根据相互增强效应［27］，如果节点k是i和j的共同邻居，那么j也会尝试激活k。这表示通过节点j，节点i成功激活两者共同邻居k的概率实际上是大于β的。此时，邻居节点j起到了放大器的作用，加强了节点i在本地区域内的传播效果。

其次，如果节点i存在邻居节点j，节点j存在邻居节点k，且i与k无关。信息只能通过节点j和k之间的连接对外传播，否则将被限制在节点i和j所在的本地区域。此时，节点j在信息传播过程中扮演了掮客的角色，将信息传输到网络更广泛的区域。

区分邻居节点j具体做出何种贡献的关键是节点i与j是否享有共同邻居。因此，SCCN 使用共同邻居数（common neighbors）来度量邻居节点j这2 种贡献的比例。这里给出节点i与节点j的共同邻居数cnij为：

式中，Γi是节点i的邻居节点集合。

SCCN 算法在K-shell 的基础上度量邻居节点的第一贡献，即在节点所处的紧密连接的局部区域加强传播效果。K-shell 算法是通过逐层剥离外围节点来衡量节点在网络中的中心位置，位于最内层的节点被认为是最重要的节点［5］。这种分解方式有一个很有意思的特性，即如果一个节点的K-shell 值等于x，那么这个节点一定至少处于一个有x+1 个节点组成的全连通子图中。此特性可以方便地估计一个节点所在的连接紧密的本地区域范围的大小，即包括节点的数量。因此，SCCN 定义网络中的任意一个节点i，基于其邻居节点的第一种贡献所获得的影响力为：

式中，Γi是节点i的邻居节点集合，cnij是节点i和节点j 的共同邻居数，kj是节点j的度值，ksj是节点的k壳数。代表的是邻居节点j对节点i重要性的贡献度，属于加强节点i在本地区域内传播效果的比例。同时，考虑到节点所处的本地区域大小和紧密程度都是有上限的，随着与节点i具有共同邻居的邻居节点j增多，邻居节点j对i的贡献会逐渐衰减，因此SCCN对这一部分的影响取了对数。

对于邻居节点的第二种贡献，扩展节点所携带的信息至网络其他区域，SCCN 选择基于节点的度值和共同邻居数去度量。与第一贡献相比，第二贡献是为了促进信息在整个网络中的传播，其作用应该更加重要，所以取指数形式。因此，SCCN定义网络中的任意一个节点i，基于其邻居节点的第二种贡献所获得的影响力为：

最终，网络中任意一个节点i基于其邻居计算得出的影响力为上述2种贡献的组合：

接下来，为了更清楚地阐述SCCN 的计算流程，本文将以图1中的节点v5为例展示计算过程。

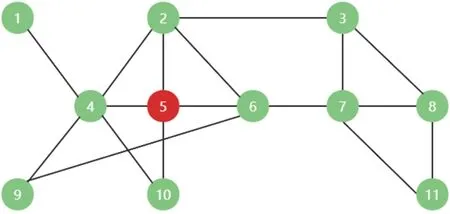
图1 一个具有11个节点与17条边的示例网络

节点v5的邻居节点包括节点v4、v2、v6和v10。根据公式（2），计算出节点v5与其邻居节点之间的共同邻居数：cn5，4=2、cn5，2=2、cn5，6=1、cn5，10=1。根据公式（3），计算出节点v5基于其邻居第一种贡献所获得的影响力为：

根据公式（4），计算出节点v5基于其邻居第二种贡献所获得的影响力为：

最后，根据公式（5），可以计算出节点v5的SCCN值为：

示例网络中其他节点的SCCN 值按照相同的流程计算。表1 展示了示例中每个节点的DC、BC、Kshell、PR和SCCN值。

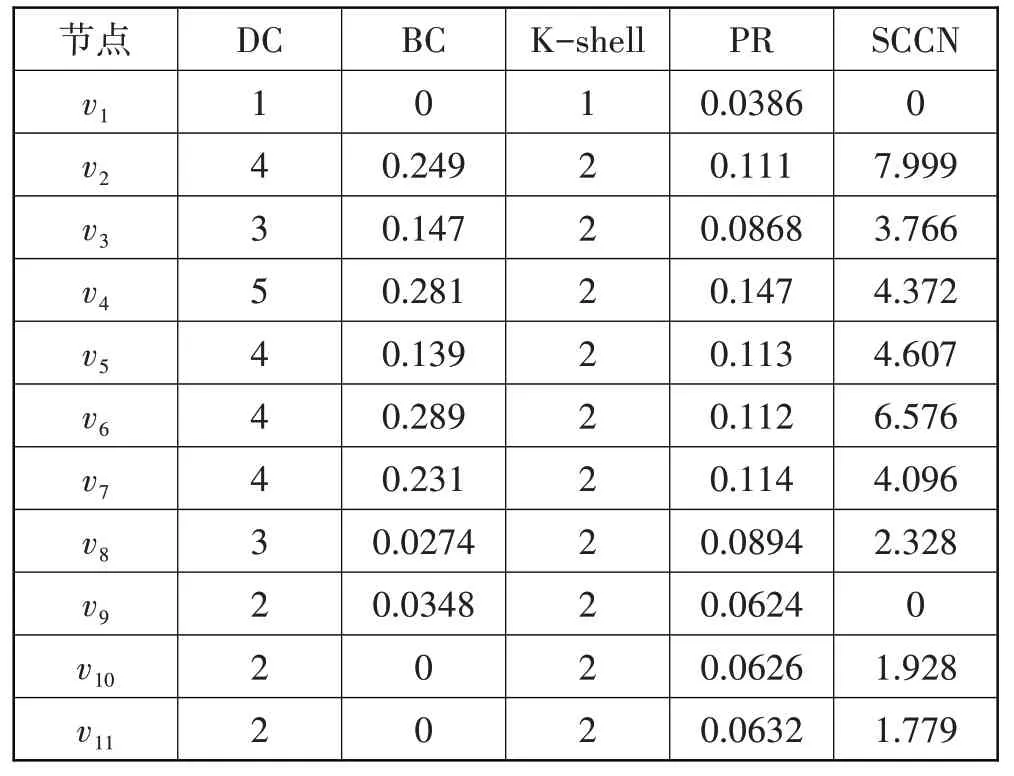
表1 示例网络11个节点不同中心性的值

从这个示例网络来看，按照SCCN 值的排序结果为v2、v6、v5、v4、v7、v3、v8、v10、v11、v1、v9；按照BC 的排序结果为v6、v4、v2、v7、v3、v5、v9、v8、v1、v10、v11；按照PR 的排序结果为v4、v7、v5、v6、v2、v8、v3、v11、v10、v9、v1。在SCCN 排序结果中，排名第一的节点是v2，其在按BC和PR 的排序结果中分别排名第3 和第5。节点v1和v9的计算结果是0，因为示例网络中不存在以它们为顶点的三角形，导致local1和local9等于0。事实上，这2 个节点在按照BC 和PR 的排序结果中也处于较后的位置。此外，在这个示例网络上，有许多节点享有相同的度值和K-shell 值，粒度较粗，但是SCCN 不存在这一问题。

3 实验分析

3.1 数据集

为了验证SCCN 的有效性，本文选取8 个真实世界网络样本对SCCN与同类算法进行对比：

1）power，一个代表美国西部州电网拓扑结构的网络。

2）Email-Enron，一个来自Enron 公司的电子邮件通讯网络。网络的节点是电子邮件地址，如果一个地址i至少向地址j发送了一封邮件，那么该图就包含一条从i到j的无向边。

3）Wiki-Vote，一个包括维基百科投票数据的网络。

4）musae-squirrel，一个Facebook 网站的页-页图。节点代表Facebook的官方网页，而链接是网站之间的相互喜欢。该图是在2017 年11 月通过Facebook Graph API收集的。

5） CA-CondMat，一个协作网络，数据涵盖了1993年1月至2003年4月（124个月）期间提交给Condense Matter Physics的论文作者之间的科学合作。

6）CA-HepPh，一个协作网络，数据涵盖1993 年1 月至2003 年4 月（124 个月）期间提交给High Energy Physics-Phenomenology 的论文作者之间的科学合作。

7）p2p-Gnutella24，一个2002 年8 月24 日收集的Gnutella点对点文件传输网络。

8）p2p-Gnutella25，一个2002 年8 月25 日收集的Gnutella点对点文件传输网络。

上述这些网络样本均来自Stanford Large Network Dataset Collection。在实验过程中，如果发现某一网络并不是连通的，则使用其最大连通分量。这些网络的高级特征由表2（其中N表示节点数、M表示边数、D表示平均度、L表示平均最短路径、C表示平均聚类系数）展示。

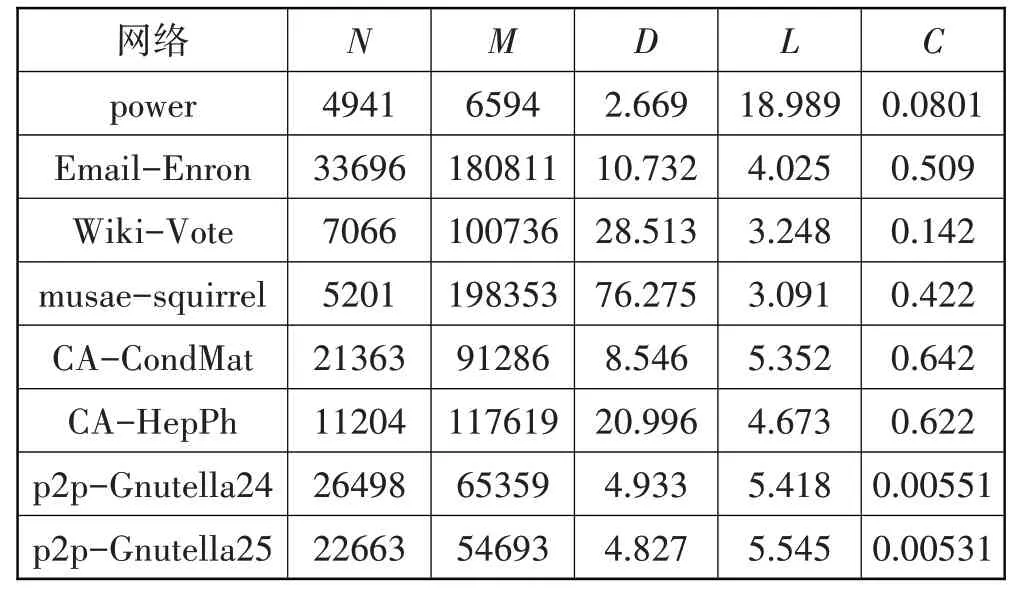
表2 8个真实世界网络的结构特征

3.2 实验结果

一般来讲，越重要的节点在传播过程中能够激活越多的节点。因此，为了验证本文提出算法的准确性，本文选择使用标准SIR 模型来计算不同重要节点发现算法在多个真实世界网络上的模拟结果。

在标准SIR模型中，网络上的节点被分为3类：

1）易感者（S），此类节点没有被感染，但是其缺乏免疫力能被邻居节点中的感染节点以特定概率β感染。

2）感染者（I），此类节点已经被感染，同时以一定的概率感染其邻居节点。

3）恢复者（R），此类节点从感染中恢复并得到免疫能力，在后续传播过程中不会再被感染。

在开始阶段，k个节点被设为种子节点，是感染源。所有其他节点被设置为易感节点。在接下来的每一个单位时间步长内，感染者节点都以特定的概率β去感染易感邻居节点。同时，感染者节点以特定的概率γ恢复。重复此过程，直到网络中没有易受影响的节点为止。这里定义关于时间步长t的函数F（t），表示在时间t内网络上感染节点与恢复节点之和占总节点的比重，即代表了传播规模。显然，F（t）的值会随着时间t逐渐收敛，最终达到一个稳定状态，此时传播过程结束。F（t）越高，表明种子节点的影响力就越大。通过选择不同节点作为初始种子节点，并比较传播结束时的F（t）值，可以得出不同种子节点的影响力大小。

在这些实验中，根据度中心性（DC），K-shell（KS），介数中心性（BC），PageRank（PR）和SCCN 计算出每个真实网络上节点的重要性顺序。由于本文的研究更关注网络中的超级传播者，因此选择重要性排名前10的节点作为初始种子节点，根据标准SIR模型进行数值模拟。最终的F（t）是在重复计算1000 次后取的平均值。

表3 中的数据表明，在power 中，SCCN 计算排名第1 的节点是2553，在DC 和PR 中分别排名第1 和第4。SCCN 计算排名第2的节点是4458，在DC 和PR 中分别排名第2 和第1。在SCCN 中排名第3 和第5～第8 的节点则在DC、BC 和PR 中均未出现。在CAHepPh 中，SCCN 认为排名第2 的节点是19732，在BC和PR 中都排名第1。SCCN 认为排名第2 的节点是29392，在BC 和PR 中都排名第5。SCCN 认为排名第5 的节点是28271，在BC 和PR 中都排名第3。而SCCN 中排名第1、第4和第6～第7的节点均未在其他算法中出现。这些迹象表示SCCN 能够识别出在其他同类算法中排名较前，出现次数较多的节点，又能发现其它算法无法识别的潜在重要节点。

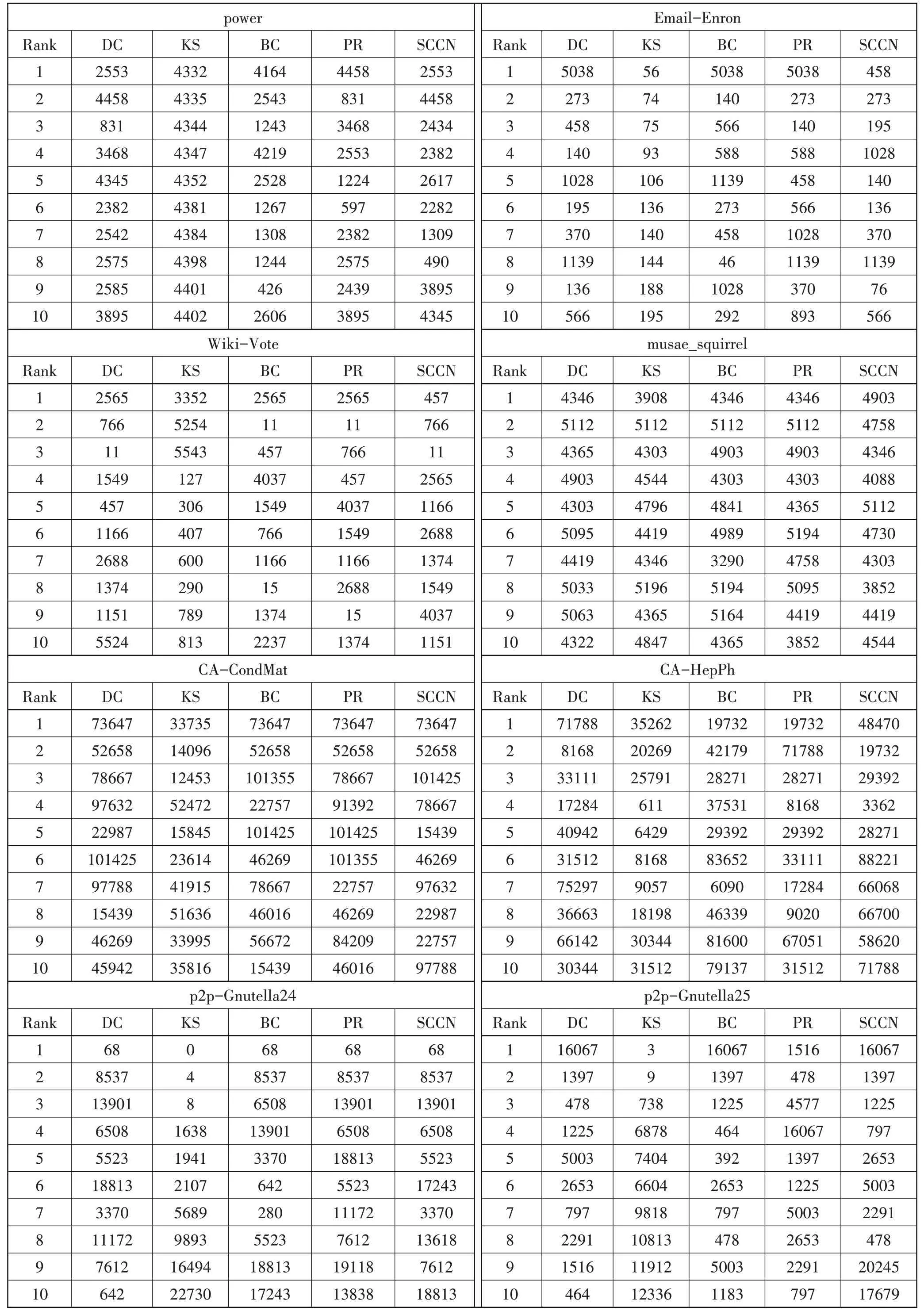
表3 根据DC、BC、K-shell、PageRank和SCCN排序得出的top-10节点编号

图2（图中横坐标表示SIR 模拟的时间步长，纵坐标表示感染节点与恢复节点所占的比例）清楚地表明，通过SCCN 选择出的种子节点，相比于其他算法，在SIR 模拟的整个传播过程中能够感染更多的节点，这表示通过SCCN 选择出来的节点更加重要，SCCN具有更高的精确性。在图2（b）中，迭代停止时，（I+R）/N最大的是代表SCCN的曲线。这代表SCCN算法在Email-Enron 上表现得最优。DC 的表现弱于SCCN，再之后则是BC、PR 和K-shell。在图2（e）中，同样是SCCN 表现得最优，之后是PR、BC、DC 和Kshell。这说明SCCN选择的种子节点有效地扩大了信息的传播规模。

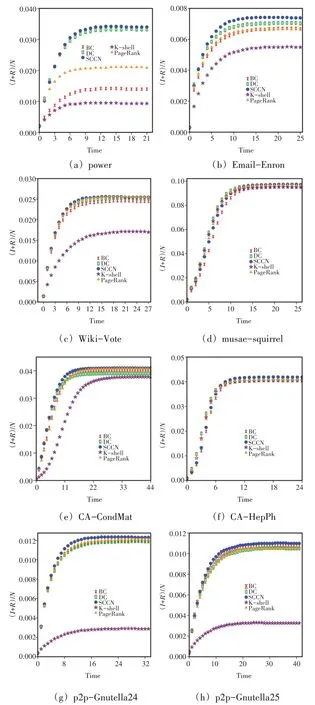
图2 DC、BC、K-Shell、PageRank和SCCN在8个真实世界网络上的SIR模拟结果

此外，在一些网络上，迭代停止时，BC 与PageRank二者之间（I+R）/N更大的是BC，这说明BC表现得比PageRank 更优，如图2（f）和图2（h）所示；在另一些网络上，PageRank 表现得比BC 更优，如图2（a）和图2（c）所示；也有一些网络，两者表现的差不多，如图2（b）所示。而SCCN 虽然在图2（c）和图2（d）中与BC、PageRank 很接近，但在各个网络样本上都能保证处于最优水平。这些现象说明，BC 和PageRank 在不同的网络上的稳定性不如SCCN。

最后，本文对SCCN 的时间复杂度进行简要的分析。SCCN 的时间复杂度由3 个部分组成：1）计算节点之间共同邻居数；2）计算节点K-shell值；3）计算节点度。对于第1 部分，算法需要遍历每个节点邻居的邻居，因此其平均复杂度大致为O（N＜k＞2），其中N代表给定网络的节点数，＜k＞代表所有节点的平均度数。K-shell 算法的复杂度为O（N）。计算节点度数的复杂度为O（N）。那么SCCN 的总时间复杂度为O（N＜k＞2+N+N），相对于复杂度为O（MN）的介数中心性和复杂度为O（N2）的PageRank 来说是比较低的。这代表SCCN能更好地适用于大规模网络。

4 结束语

本文提出了一种基于节点邻居信息的重要节点发现算法SCCN。相较之前的算法并没有很清楚地划分邻居节点的具体作用，受到PageRank 算法的启发，SCCN 算法进一步结合节点的共同邻居数和K-shell值去开展度量。结合传播过程的动态特点，SCCN 算法将邻居节点的作用分成2 类：1）加强该节点所在的连接紧密的本地区域内的传播效果；2）扩展该节点所携带的信息至网络其他区域。此外，在真实世界网络上进行的大量实验明确表明，本文所提出的算法优于现有的知名排序算法，同时具有较低的时间复杂度，让SCCN 可适用于大规模网络。SCCN 算法不足在于，其在衡量邻居节点的第2 种作用时，基本上是平等地对待每一个节点。这么做虽然使得SCCN 的计算复杂度较低，但也令其损失了一部分精确性。下一步的工作将会考虑在保证相对较低的计算复杂度的前提下，基于网络的局部结构更精确地衡量邻居节点的第2种作用。