基于韧性断裂准则的AZ31B镁合金板材成形极限预测

张瑞昭 孔博炜 崔忠冠 陈伟 任丽梅

摘要：结合损伤起始判据和损伤演化准则，建立了完整的韧性断裂准则，基于ABAQUS中韧性损伤材料模型对AZ31B镁合金板材成形极限进行了预测。通过拟合单向拉伸应力应变曲线得到材料本构模型及损伤演化参数，建立了板材的Nakazima半球形凸模胀形有限元仿真模型，再基于韧性断裂准则预测了AZ31B镁合金板材室温下的成形极限，并分析了不同板材断裂失效判据对成形极限的影响。研究结果表明，基于所建立的韧性断裂准则，并以损伤演化过程中应变路径转变作为断裂失效判据，可以较准确地预测镁合金板材成形极限，得到的成形极限图与实验结果吻合较好。

关键词：损伤准则；韧性断裂准则；AZ31B镁合金；成形极限

中图分类号： TG386文献标识码： ADOI：10.3969/j.issn.1007-791X.2024.01.0020

引言

金属板材冲压成形是一种广泛应用于汽车、航空航天、仪器仪表等领域的塑性加工工艺。板料成形极限是板料成形重要的性能指标，它全面反映了板料在单向和双向拉应力作用下抵抗颈缩或破裂的能力，是评价其零件成形质量好坏和工艺设计合理性的重要指标。成形极限图（Forming limit diagram，FLD）为方便研究板料成形极限、评价板料成形性能和解决板料成形领域中的难题提供了技术基础和实用判据[1-2]。

随着轻量化进程的推进，先进高强钢、铝合金、镁合金等结构板材在汽车、航空航天等工程领域得到了越来越广泛的应用[3-4]。但与普通钢板相比，一些轻量化材料延展性较差，观察不到明显的颈缩现象。采用基于拉伸失稳理论或分叉理论建立的颈缩模型（Hill[5]、Swfit[6]等）不能准确地来预测板材在加工过程中的斷裂情况[7-8]。而韧性断裂准则是以损伤力学为基础的，以材料内部微观孔洞成核、成长、聚集引起的累积损伤为材料失效判据，从而能够准确判断出材料的失效点。因此，研究学者提出了采用韧性断裂准则来预测轻量化材料的板材成形极限，以期更好地预测轻量化金属的断裂情况。

Takuda等[9]运用Cockcroft-Latham准则[10]、Brozzo准则[11]、Oyane韧性断裂准则[12]对铝合金板材和低碳钢板料轴对称拉深进行模拟预测，其预测结果与实验结果各区域均符合较好。余心宏等[13]使用Oyane韧性断裂准则成功预测了铝合金A5182和SPCC钢板的成形极限。翟妮芝等[14]在Lemaitre的理论基础上建立韧性断裂准则成功预测了A5754和SPCC两种板材的成形极限。Dizaji等[15]考虑了材料参数对成形极限曲线的影响建立了新的韧性断裂准则，并通过实验验证了该韧性断裂准则对于铝合金、钢等材料断裂预测的有效性。张赛军等[16]使用DF2012韧性断裂准则成功预测了DP590高强钢在不同应力状态下拉伸试样的断裂。

目前，对于高强钢、铝合金材料韧性断裂准则研究较多，并在实际中应用较为广泛，但对于镁合金板材的成型极限大多是基于早期的颈缩模型提出来的，基于韧性断裂准则研究较少。镁合金板材成形极限反映出镁合金板材的最大成形能力，不仅能够判断零件的可加工性，还可以判断材料的性能能否得到充分利用，为实际生产过程中镁合金材料的选择和工艺设计的合理性提供重要的参考依据。因此，本文以Kolmogorov[17]文中应用的断裂准则作为损伤起始判据并结合Bai等[18]提出的损伤演化准则，建立了完整的韧性断裂准则；结合有限元模拟软件对AZ31B镁合金Nakazima胀形过程进行了模拟；基于在板材的局部失稳区域其应变路径会向平面应变状态转变的现象，以板材在损伤过程中应变路径转折点为判据对板材的成形极限进行了预测。

1材料模型

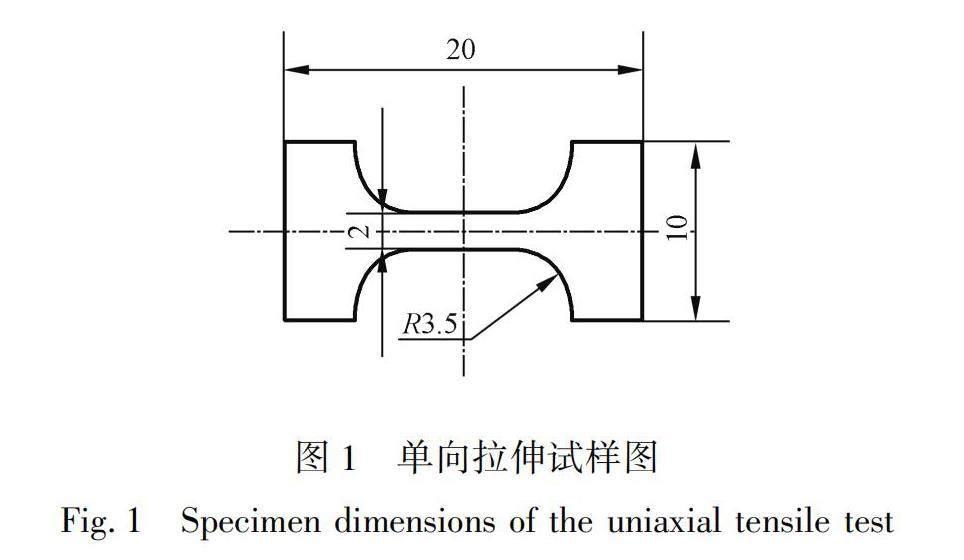
本文实验材料为厚度为1 mm的AZ31B镁合金轧制板材，沿板材轧制方向切取单向拉伸试样进行单向拉伸实验，试样尺寸如图1所示。单向拉伸实验在Inspekt table 100 kN电子万能试验机上进行，拉伸速度为0.3 mm/min，得到的工程应力应变曲线如图2所示。

第1期张瑞昭等基于韧性断裂准则的AZ31B镁合金板材成形极限预测

燕山大学学报2024

由于镁合金轧制板材通常具有很强的各向异性，因此，本文采用了Hill48[19]屈服准则，如下式所示：

式中，F、G、H、L、M、N为各向异性特征参数，可由厚向异性系数计算得到，如表1所示[20]。

运用Hollomon[21]本构方程描述板材的应力应变关系，其公式如下：

σ=Kεnp，    （2）

式中，σ、n、εp、K分别为真实应力、硬化指数、真实塑性应变、强度系数。

利用单向拉伸实验数据对式（2）进行拟合，如图3所示，可获得板材的塑性参数如表2所示。

2韧性断裂准则

2.1韧性断裂准则的建立

本文以Kolmogorov提出的韧性断裂准则作为板材的损伤起始判据，构建板材损伤起始时刻的等效塑性应变与应力三轴度的关系，即

材料损伤演化应力应变曲线如图4[22]所示，随着塑性变形的增加，当损伤起始判据逐渐累积达到1时，认为板材开始损伤。图中虚线是根据理想的弹塑性本构方程获得的曲线，实线为实际具有损伤段的实验曲线，当塑性变形继续进行时，板材开始损伤演化，损伤演化过程中实际应力值会因为刚度退化与理想弹塑性曲线存在一定差值，根据该差值拟合出损伤演化系数D与应变的关系，来定义材料损伤演化的阶段。

构建板材在损伤过程中的损伤演化系数与等效塑性应变的关系：

板材的实际损伤演化更趋向于指数型损伤演化，在损伤起始阶段，板材损伤指数增长缓慢，而在损伤演化后续阶段，损伤指数急剧增加，具体表达式如下：

式中，a、b为损伤演化参数。

当板材的塑性变形满足设定的损伤起始判据时，板材开始损伤，在损伤起始阶段，刚度降低较缓慢，应变硬化效应和刚度退化效应维持平衡，导致板材所能承受的载荷维持在最大载荷力附近。随着塑性变形的增加，损伤演化系数指数增长，板材的刚度开始急剧下降，从而导致板材所能承受载荷力也急剧下降，最终导致板材的断裂失效。

2.2断裂损伤准则参数确定

从损伤起始判据中可知，板材的损伤起始时刻的等效塑性应变与板材的应力三轴度密切相关，参考廖解放[23]提出AZ31B镁合金板材的应力三轴度与等效塑性应变的关系得到：

式中，?=εp-0.114 93为修正参数。

修正后的应力三轴度与等效塑性应变的关系如图5所示，可以看出材料在不同的应力三轴度下其所表现出的断裂行为并不相同，韧性断裂准则的准确性也与此有很大的联系。

当板材开始损伤后，其损伤演化系数D与等效塑性应变p呈指数增加。在ABAQUS有限元软件中，按照实验加载情况设定边界条件，利用建立的理想弹塑性模型Hollomon材料模型与实际拉伸数据对式（5）进行拟合求解即可得到试样的损伤演化参数，试样的损伤演化参数拟合过程如图6所示，拟合参数a为1 634.3，b为4.175 8。最后将获得的应力三轴度与断裂应变关系以及损伤演化系数输入到ABAQUS中韧性材料损伤模型中，实现有限元的应用。最终拟合结果如图7所示，可以看到所建立的韧性断裂准则在有限元中能较好地模拟单向拉伸过程的变形过程。

3有限元模型

3.1几何模型

依据GB/T 15825.8—2008《金属薄板成形性能与试验方法》[24]，建立了Nakazima半球形凸模胀形有限元仿真模型，如图8所示，几何参数如表3所示。假定模具为刚体，对拉延筋进行简化，对板料外边界进行固定，以限制拉延筋以外的板料向里流动，仅靠胀形区域材料自身的金属流动实现塑性变形，在试样刚出现裂纹时立即停止凸模运动[25]。

3.2多应变路径试样设计

在板材成形极限实验过程中，通常采用不同长宽比的试样进行胀形来实现不同的应变路径，从而获得各种应变路径下的极限应变值并在（ε2-ε1）主应变坐标系中描绘各应变路径下的极限应变点（ε2，ε1），通过拟合极限应变点得到成形极限图。本文所采用的试样几何形状如图9所示[26]，几何尺寸如表4所示。

3.3接触和边界条件

在半球形凸模胀形实验中，使用润滑剂也无法完全消除模具和板材之间摩擦的影响。因此，在有限元模型中也设置了模具和板材之间的摩擦参数[27]。模拟过程中采用固定凹模，给定压边力，凸模位移的边界条件。模型中所设置的接触参数及边界条件如表5所示。

3.4单元类型

在板材成形有限元模拟中，可使用的单元类型有三维实体单元、壳单元和薄膜单元等。采用三维实体单元对板材进行有限元分析，会导致模型的单元和节点数量成倍增加，导致计算的时间成本过高，而计算精度相对于壳单元却无显著差别。对于平面尺寸远大于其厚向尺寸的薄板，往往选用壳单元，既能保证结果精度，又能节省计算时间。因此，本文采用ABAQUS软件中的S4R减缩积分单元，单元尺寸约为0.33 mm，在厚度方向设置5个Simpson类型的积分点，模具在模型中设置为刚体。

4模拟结果分析

4.1准静态模拟工况的验证

ABAQUS/Explicit模块采用显示方法计算，适合于动力学过程分析，如高速碰撞问题，其中惯性力对模型的影响显著。Explicit模块也可以分析准静态问题，但若依据准静态成形的真实时间进行模拟，需要计算的时间增量可达到上百万步。因此，为了节约计算成本，一般采用固定冲压行程并提高凸模的冲压速度，从而缩短板材的成形时间。由于冲压速度提高，模型从静平衡分析转变为动平衡分析，惯性力对模型的影响提高了。因此，为了保证Explicit模块进行准静态分析的准确性，需要将惯性力的影响维持在较低水平，而判断方法则采用能量平衡方程，如下所示：

式中，EKE、El、EV、EFD、EW、EPW、ECW、EMW、ETOT分别为动能、内能、粘性机制耗散能、摩擦耗散能、外力功、接触产生的能量、约束产生的能量、质量缩放产生的能量、系统总能量。

在准静态响应中，由于板材变形速度很慢，板材的惯性力可以忽略不计，板材的动能也微乎其微，则外载荷做功近似全部转化成板材的内能。当提高凸模冲压速度，板材响应偏离准静态而转变为动态，板材的惯性和动能急剧增加，由于系统总能量为常数，导致板材内能占比急剧降低。通常当板材的动能占比不能超过其内能的5%时，认为板材为准静态响应。

用板材几何尺寸编号为1的试样进行冲压的有限元模拟，如图10所示，从图中可知，当凸模的冲压速度为100 mm/s时，动能与内能相比仅占很小一部分，近似为零，因此认为此模型为准静态响应。

4.2成形极限图

板材成形极限图获取的关键点在于板材的极限应变点的确定。选取AZ31B镁合金板材胀形过程中即将断裂时刻的最大等效应变节点，分析其应变路径的演化过程，如图11所示，可见板材在失效前，其应变路径会向平面应变路径转变。因而，为了比较不同判据对成形极限预测的影响，分别选取了板材即将断裂时刻和应变路径转变时刻作为板材的极限应变点，并依次确定各试样的成形极限点，如图12所示（仅展示了表4中编号1、5、9试样在应变转折时的成形极限点），然后根据不同应变路径下各试样的极限应变绘制出两种判据下的成形极限图。

图13是预测得到的板材成形极限图，与实验所得结果[28]进行对比分析可以看出，以应变路径转变时刻的成形极限图与实验结果吻合较好，而以断裂时刻为判据的成形极限图远高于实验值。这是由于当板材开始损伤后，板材的刚度逐渐削弱，导致板材局部区域成为承载能力最薄弱區域，该局部区域的单元开始失稳，单元节点的应变急剧增加，使得断裂时刻的应变值超过了材料的极限应变值，这也导致应变路径向平面应变路径发生了转变，当塑性变形继续增加，板材刚度继续退化直到无法支撑变形，从而导致板材的断裂失效。因此，板材的应变路径转变时刻早于板材的断裂失效时刻，也更接近于板材在实际成形过程中的断裂时刻。

5結论

1） 镁合金AZ31B板材的应变路径转变依赖于板材的起始损伤时刻和损伤演化过程，当板材的刚度急剧退化时，板材的应变路径转变显著。

2） 建立了完整的韧性断裂准则，结合ABAQUS中韧性损伤材料模型对板材成形极限进行了预测，结果表明该韧性断裂准则可以用于镁合金板材断裂失效行为的预测。

3） 在成形极限预测过程中，采用应变路径转变作为断裂失效判据，能够更准确地预测镁合金AZ31B板材成形极限，而基于板材断裂时刻的成形极限判据预测的成形极限远大于实验结果。

参考文献

[1] 柯俊逸.复杂加载条件下金属板料的成形极限研究 [D].武汉：华中科技大学，2018.

KE J Y. A Dissertation submitted in partial fulfillment of the requirements for the degree of philosophy in engineering [D]. Wuhan：Huazhong University of Science and Technology，2018.

[2] 余胜娟，周旭东.板料成形性的研究现状和发展趋势[J].锻压装备与制造技术，2007（6）：14-17.

YU S J，ZHOU X D. Research state and its development trends of sheet metal workability [J].China Metal forming Equipment & Manufacturing Technology，2007（6）：14-17.

[3] XU T，YANG Y，PENG X，et al. Overview of advancement and development trend on magnesium alloy[J]. Journal of Magnesium and Alloys， 2019，7（3）： 536-544.

[4] 郭丽丽，郭浩然，汪建强，等.轧制工艺对连续挤压AZ31镁合金板材成形性的影响[J].塑性工程学报，2021，28（7）：56-63.

GUO L L，GUO H R，WANG J Q，et al. Influence of rolling process on formability of continuously extruded AZ31 magnesium alloy sheets [J].Journal of Plasticity Engineering，2021，28（7）：56-63.

[5] 王贵开.基于韧性断裂准则的AA5182-O铝板成形极限预测[D].秦皇岛：燕山大学，2021.

WANG G K. Forming limit prediction of AA5182-O aluminum sheet based on ductile fracture criterion [D]. Qinhuangdao： Yanshan University，2021.

[6] 金英锡，吕晓东，肖潇，等.高强度钢板的成形特性及成形技术现状[J].汽车工艺与材料，2016（9）：46-53.

JIN Y X，L? X D，XIAO X，et al. Forming characteristics and current status of forming technology of high-strength steel plates[J].Automobile Technology and Materials，2016（9）：46-53.

[7] HILL R T. On discontinuous plastic states，with special reference to localized necking in thin sheets[J]. Journal of the Mechanics and Physics of Solids，1952，1（1）： 19-30.

[8] SWIFT H W. Plastic instability under plane stress[J]. Journal of the Mechanics and Physics of Solids，1952，1（1）： 1-18.

[9] TAKUDA H，MORI K，HATTA N. The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals[J]. Journal of Materials Processing Technology，1999，95（1/2/3）： 116-121.

[10] COCKCROFT M G. Ductility and workability of metals[J]. Journal of Metals，1968，96： 2444.

[11] BROZZO P，DELUCA B，RENDINA R. A new method for the prediction of formability limits in metal sheets[C]//Proceedings of the 7th Biennial Conference of the IDDR，Amesterdan，1972.

[12] OYANE M，SATO T，OKIMOTO K，et al. Criteria for ductile fracture and their applications [J]. Journal of Mechanical Working Technology，1980，4（1）：65-81.

[13] 余心宏，翟妮芝，翟江波.应用韧性断裂准则预测板料的成形极限图[J].锻压技术，2007（5）：44-47.

YU X H，ZHAI N Z，ZHAI J B. Prediction of sheet metal forming limit diagram by applying ductile fracture criterion [J]. Forging & Stamping Technology，2007（5）：44-47.

[14] 翟妮芝.数值模拟在板材成形極限分析中的应用[D]. 西安：西北工业大学，2007.

ZHAI N Z. Application of numerical simulation to the analysis of the forming limit of sheet metals [D]. Xi′an： Northwestern Polytechnical University，2007.

[15] DIZAJI S A，DARENDELILER H，KAFTANOGLU B. Prediction of forming limit curve at fracture for sheet metal using new ductile fracture criterion[J]. European Journal of Mechanics-A/Solids，2018，69： 255-265.

[16] 张赛军，李康镇，张昆，等.韧性断裂准则参数标定及其在DP590中的应用[J].哈尔滨工业大学学报，2021，53（1）：63-69.

ZHANG S J，LI K Z，ZHANG K，et al. Parameter calibration of ductile fracture criterion and its application on DP590 [J]. Journal of Harbin Institute of Technology，2021，53（1）：63-69.

[17] KOLMOGOROV W L. Spannungen deformationen bruch[J]. Metallurgija，1970，9：230.

[18] BAI Y，WIERZBICKI T. A new model of metal plasticity and fracture with pressure and Lode dependence[J]. International Journal of Plasticity，2008，24（6）： 1071-1096.

[19] HILL R. A theory of the yielding and plastic flow of anisotropic metals[J]. Proceedings of the Royal Society of London. Series A， Mathematical and Physical Sciences，1948，193（1033）： 281-297.

[20] 于勇.AZ31B镁合金板材拉伸力学性能的各向异性研究[D].大连： 大连海事大学，2009.

YU Y. Study on anisotropy of AZ31B magnesium alloy sheet based on tensile mechanical test [D]. Dalian： Dalian Maritime University，2009.

[21] ZENER C，HOLLOMON J H. Effect of strain rate upon plastic flow of steel [J].Journal of Applied Physics，1944，15（1）： 22-32.

[22] 钱让发. 白车身热熔自攻丝工艺参数的分析与优化[D]. 合肥：合肥工业大学，2019.

QIAN R F. Analysis and optimization of flow drill screwdriving process parameters for body-in-white [D]. Hefei：Hefei University of Technology，2019.

[23] 廖解放.AZ31B镁合金准静态下应力三轴性对断裂行为的影响[D].绵阳： 西南科技大学，2017.

LIAO J F. Influence of stress triaxiality on the fracture behavior of AZ31B magnesium alloy under quasi-static loading [D]. Mianyang： Southwest University of Science and Technology，2017.

[24] 中国机械工业联合会.金属薄板成形性能与试验方法：第8部分  成形极限图（FLD）测定指南： GB/T 15825.8—2008[S]. 北京：中国标准出版社，2018.

China Machinery Industry Federation.Sheet metal form ability and test methods：Part 8  Guidelines for the determination of forming-limit diagrams：GB/T 15825.8—2008[S]. Beijing：China Standard Press，2018.

[25] 韩俊超，董晓传，曲周德，等.5182铝合金板材成形性能研究[J].塑性工程学报，2020，27（2）：87-93.

HAN J C，DONG X C，QU Z D，et al. Study on formability of 5182 aluminum alloy sheet [J]. Journal of Plasticity Engineering，2020，27（2）：87-93.

[26] 陈崇乾.基于Nakazima試验的铝合金板材AA5086成形极限研究[D].济南：山东大学，2018.

CHEN Q K. Research on forming limit for AA5086 aluminum alloy sheet based on Nakazima test [D]. Jinan： Shangdong University，2018.

[27] 李文娟.AZ31B镁合金板料成形性能研究[D].济南：山东大学，2012.

LI W J. Research on the formability of AZ31B magnesium alloy sheet [D] Jinan： Shandong University，2018.

[28] HUANG G，ZHANG H，GAO X，et al. Forming limit of textured AZ31B magnesium alloy sheet at different temperatures[J]. Transactions of Nonferrous Metals Society of China，2011，21（4）：836-843.

Prediction of forming limit of AZ31B magnesium alloy sheet

based on ductile fracture criterion

ZHANG Ruizhao1，2，KONG Bowei1，2，CUI Zhongguan1，2，CHEN Wei1，2，REN Limei1，2

（1.Key Laboratory of Advanced Forging & Stamping Technology and Science（Yanshan University），

Ministry of Education of China，Qinhuangdao，Hebei 066004，China;

2.School of Mechanical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China）

Abstract：Combining the damage initiation criterion and the damage evolution criterion，a complete ductile fracture criterion was established to predict the fracture failure of the sheet. The constitutive model and the damage evolution parameters were obtained by fitting the uniaxial tension stress-strain curve. The finite element model was established based on the Nakazima hemispherical punch bulging experiment，and the ductile fracture criterion was used to predict the forming limit diagram （FLD） of AZ31B magnesium alloy at room temperature. The influence of the fracture failure criterion and strain path transition criterion on the prediction of forming limit diagram was discussed. The results indicated that by using the strain path transition during the damage evolution as the fracture failure criterion，the predicted FLD is in good agreement with the experimental results.

Keywords：damage criterion; ductile fracture criterion;AZ31B magnesium alloy; forming limit