门限密码技术及其标准化进展*
2024-04-28荆继武张世聪王平建
荆继武, 张世聪, 王平建,2
1.中国科学院大学 密码学院, 北京 100190
2.中国科学院 信息工程研究所, 北京 100085
1 引言
门限密码为开放的或不够安全的环境中的密码计算提供了一种更加安全的解决方案.门限密码的目标在于, 当少数几个设备被攻破或被敌手占领后, 密码的执行仍旧是有安全保障的, 也就是说, 密钥不会泄漏, 密码功能能够正常进行.
近年来, 门限密码安全性潜力的凸显使其被关注度日渐增加.研究者们在门限密码领域, 针对门限密钥生成、门限密码计算等方向提出了大量相关的新技术、算法和协议.RSA 签名算法相对比较简单, 研究者们很早对其门限计算做了许多研究, 近年来新的成果较少, 主要集中在RSA 参数的多方生成.ECDSA算法由于计算签名时要用到随机数的逆, 因此设计其对应的门限算法时需要引入零知识证明、同态加密、不经意传输或Beaver 三元组乘法等较重的技术, 不但增加了较大的计算量和带宽的开销, 也引入了另外的安全假设.Schnorr 与EdDSA 类门限密码算法在计算签名时, 私钥和随机数使用都是线性多项式, 因此是门限友好的, 其对应的门限算法实现起来较为容易, 不过EdDSA 使用确定性算法产生随机数, 这是设计其对应的门限算法时要重点考虑的.SM2 算法在签名时也使用了非线性的多项式, 这也为其对应的门限算法的设计带来了困难, 不过可以通过变换将签名公式等价为更友好的形式, 基于此设计的SM2 协同签名算法已经成为我国商用密码产业生态的重要一环.同时, 门限密码的标准化工作也在国际范围内展开,这些工作将对门限密码技术的应用产生深远影响.双线性对和格密码的门限算法也是近来的研究热点, 基于双线性对的签名在密码学的短签名、基于身份的签名中有重要应用.格密码由于运算复杂度相对较低,且签名大小相对较小, 被认为是一种合适的抗量子密码方案.
本文将从门限密码的基本元素、门限密码算法和协议、门限密码的标准化及应用三个方面展开.基本元素部分将介绍我们对门限密码技术的理解、门限密码的构成以及面临的主要问题.在算法和协议部分,由于不同类别的算法在设计对应的门限方案时存在较大差异, 因此将按照算法归类分别介绍基于RSA、ECDSA、Schnorr 与EdDSA 类、SM2、双线性对和格密码等算法的门限密码算法相关工作和最新研究成果, 探索门限密码技术方面的各类评价指标, 如其性能、安全性, 并分析其差异.在标准化进程部分, 本文将描述当前各机构组织为标准化所做的工作, 并指出可能的标准化方向.此外, 本文还将讨论门限密码学的实际应用场景, 以及在实际应用中面临的挑战.
2 门限密码的基本元素和框架
一个(n,t) 门限密码(其中n ≥t) 方案包含n个成员,t称为门限值或阈值, 至少t个成员联合才能恢复秘密或完成密码计算.门限密码方案一般基于公钥密码算法, 常见的公钥密码算法包含加密、解密、签名和验签等计算.由于加密和验签计算使用公钥就可以完成, 因此常见的门限密码方案多为门限解密方案(往往也被称为“门限加密方案”) 和门限签名方案.门限密码方案使用秘密分享技术在多个成员之间分享私钥和联合计算中的一些敏感参数.一个(n,t) 门限密码方案通常会基于一个(n,t) 秘密分享方案.(n,t) 秘密分享方案可以在多个成员之间分享一个秘密, 任意t或者t个以上的成员一起可以恢复分享的秘密, 任意少于t个成员一起不能得到秘密的任何信息.使用分享的秘密进行联合计算是门限密码方案的核心, 其特点是在联合计算过程中不恢复秘密, 且单个计算结果也不会泄露单个成员的秘密份额.
2.1 门限密码方案
一个完整的(n,t) 门限密码方案通常包括以下三个算法:
(1) KeyGen, 密钥生成算法.该算法是一个分布式密钥生成算法, 输入参数为安全参数λ、参与者数量n以及门限值t, 输出公钥pk 和n个参与者的私钥份额sk=(sk1,sk2,···,skn);
(2) ShareCom, 部分密码算法.该算法输入参数为特定参与者的密钥份额ski以及待处理数据data,输出部分结果σi;
(3) Combine, 组合算法.该算法输入参数为若干个部分结果σi, 当输入部分结果个数达到t个时, 运算并输出最终结果σ.
有时也把ShareCom 算法和Combine 算法结合起来, 统称为门限密码算法.此外, 门限密码方案还有可能包含以下三个算法:
(1) PreCom, 即预计算, 是ShareCom 算法的一个子算法.PreCom 算法的运算不依赖于待处理数据data, 因此可以独立计算;
(2) ShareVerify, 即份额判断, 是Combine 算法的一个子算法, 在正式开始Combine 前执行.该算法输入参数为公钥pk、待处理数据data 以及若干部分结果σi.该算法对输入的部分结果进行判断, 如果出现异常则中止Combine 算法;
(3) Reshare, 即重新共享份额.方案可以在适当的时候重新分配各参与者的私钥份额为sk′= (sk′1,sk′2,···,sk′n), 以确保安全性.
根据支持的密码运算不同, 门限密码方案可以分为门限解密方案和门限签名方案.门限解密方案的待处理数据是使用公钥加密的密文, 使用的密码运算是私钥解密, 例如文献[1–4] 等.门限签名方案待处理数据为待签名消息, 使用的密码运算是签名, 例如文献[5–8] 等.
2.2 安全假设和安全定义
假设敌手A 可以至多攻击n个成员中的t −1 个, 尚铭等人很好地定义了静态模型下门限密码相关安全性[2], 结合密码学常用安全性定义方法[9], 给出如下的简单安全定义, 以便读者理解:
定义1 ((n,t) 门限签名方案的不可伪造性) 给定系统参数, 敌手A 最多可以破坏t −1 个成员, 可以拥有交互运行中的视图, 可以进行至多k次适应性的选择消息m1,m2,···,mk的门限签名查询, 而最终敌手A 能伪造一个新消息m的签名的概率是可忽略的(选择消息攻击下的存在性不可伪造安全,existential unforgeability under chosen message attack, EUF-CMA).
定义2 ((n,t) 门限解密方案的保密性) 给定系统参数, 敌手A 最多可以破坏t −1 个成员, 可以拥有交互运行中的视图, 进行至多k次适应性的选择密文C1,C2,···,Ck的门限解密结果查询, 而最终敌手A 区分出两个挑战密文C和C′是否对应着相同的明文, 其概率是可忽略的(不可区分的选择密文安全,indistinguishability under chosen ciphertext attack, IND-CCA).
定义3 ((n,t) 门限签名/解密方案的健壮性) 在敌手A 最多可以破坏t −1 个成员的情况下, 方案仍然能够成功地运行.
上述定义中,k是一个关于安全参数的多项式的值.关于其他安全模型, 可参看本文2.5.3 小节“对敌手的假设”.
2.3 秘密分享与密钥生成
门限密码方案中, 一个重要的步骤就是多个成员使用秘密分享技术生成私钥或联合计算中的敏感参数.本文将私钥和敏感参数统称为秘密, 秘密按照秘密分享的数学公式被拆分成多个部分, 每一个部分被称为一个秘密份额.这里说的拆分是一个抽象的概念, 实际方案中可能并不是对一个完整的秘密进行拆分,而是每个成员独立生成自己的密钥份额.安全的方案将使得完整的秘密仅存在于概念中, 无论是在密钥生成阶段还是在联合计算阶段, 完整的秘密都不会出现.同样, 我们强调能够恢复秘密也不是真恢复秘密, 是因为要联合完成密码计算也就意味着能够恢复秘密.常用的秘密分享方法按秘密的拆分类型, 可以分为基于多项式的拆分、基于加法的拆分、基于乘法的拆分以及其他拆分方法.按照秘密份额和完整秘密之间的关系, 可以分为加性秘密分享、乘性秘密分享和其他类型秘密分享.
2.3.1 加性秘密分享

简单加法的拆分[11]将秘密拆分成多个秘密份额的和, 即如果原秘密是x, 则拆分方式为:x=x1+x2+···+xt, 其中xi为各个份额.如果n=t, 每个成员Ui拥有且仅拥有份额xi, 就形成了一个(n,n)门限方案, 也就是必须n个成员全部参与才能恢复秘密.对于一般n ≥t的(n,t) 门限方案, 存在两大类设计思路: 第一类思路是将n个份额冗余地分配给成员, 例如每个成员Ui拥有除了份额xi以外的其他份额, 则形成一个(n,2) 门限方案, 只需要2 个成员就能够恢复秘密; 第二类思路是将秘密x多次加法拆分, 每次都拆分成t个份额的和, 然后将这些份额按一定规则分配给n个成员, 分配方法需保证任意t个成员都恰好凑齐一次加法拆分所有的份额, 就能够恢复秘密.简单加性拆分的核心就是设计份额分配的规则.与多项式拆分相比, 简单加法拆分由于对于秘密的拆分和恢复均只需要进行加法运算, 而不需要多项式求值、拉格朗日插值等运算, 因此在实际使用中易于实现、运算速度快.不过由于份额的冗余分配, 需要更多的存储开销.
2.3.2 乘性秘密分享
乘性秘密分享是秘密份额和完整秘密之间存在乘法关系的一类秘密分享方法.如果原秘密是x, 则拆分方式为:x=x1x2···xn, 其中xi为各个份额.同加性秘密分享一样, 在n=t时, 只需每个成员分配一个秘密份额, 就可以形成(n,n) 门限方案; 而对于n>t的情况, 乘性秘密分享也需要将份额冗余地分给成员以满足门限恢复, 具体方法和加性秘密分享类似.秘密乘性拆分后, 在多个成员联合进行公钥密码的幂运算(RSA 中的乘方计算和椭圆曲线的点乘计算等) 时, 往往需要串行操作, 也就是后一个成员计算的输入是前一个成员计算的输出.乘性秘密分享的这种串行计算特性, 在参与计算的成员数量较多时计算效率较低, 在(2,2) 门限密码中较为常见.
2.3.3 其他类型秘密分享
也有一些门限密码方案中采用的秘密分享方法不能简单归类到加性秘密分享和乘性秘密分享.例如一个SM2 协同签名算法[12]中, 随机数k的拆分方法是k=k1k3+k2, 这是乘性秘密分享和加性秘密分享的组合应用.在另一个基于SM2 算法的协同签名方案[13]中, 随机数k的拆分方法是k=k1+d1k2,其中的d1为关于私钥的一个乘性分享份额, 也就是说不但组合使用了加性和乘性秘密分享, 还让多个秘密的分享份额之间发生了关联.
2.3.4 秘密分享下的安全密钥生成
各类门限密码方案通常会在初始阶段执行一次密钥生成算法, 为各个成员生成密钥的分享份额.
一些门限方案的密钥生成算法为了提高效率、简化协议或完成安全性证明会借助中心化的可信实体,我们称之为可信方.密钥生成时, 可信方独立生成密钥, 按照选定的秘密拆分方法将密钥拆分成密钥份额,然后将密钥份额发送给各个成员, 发送的过程中需要使用安全信道或者机密性保护技术.引入可信方能使密钥生成过程更加简洁高效, 由于仅仅在初始化时使用, 当可信方具备可证明的清除数据能力时, 带来的单点故障风险并不大.
在没有可信方参与的密钥生成算法中, 所有成员通常需要两两之间多轮交互才能完成密钥的生成, 为了满足密钥份额各成员独立掌握的需求, 往往还需要引入同态加密、多方安全计算、零知识证明等, 这带来了更多的计算量和更复杂的协议, 这也可能会成为安全的一种隐患.
2.4 门限联合计算
2.4.1 常用算法的联合计算需求
SM2 算法是我国自主研发的椭圆曲线公钥密码算法, 算法中有这样的公式:P=kG,s= ((1 +d)−1(k −rd)modq.其中d是私钥, 需要分享.而k是随机数, 获得k就能够求出d, 也必须分享保护.假设分享了d和k, 如何通过份额di、ki安全地算出s, 同时不能泄露di或者ki, 就是联合计算面临的问题.该算法联合计算需求包括单个秘密的幂运算、单个秘密求逆、两个秘密的乘法和加法.由于k是随机数, 还涉及秘密分享的生成.
ECDSA 签名算法是在90 年代初期, 作为DSA 签名算法的椭圆曲线改进版被提出的.其计算中也有类似的公式:P=kG,s=k−1(m′+rd)modq.其中k和d都需要采用秘密分享的方式分享.该算法联合计算需求包括单个秘密的幂运算、单个秘密求逆、两个秘密的乘法.该算法同样也有随机数份额的安全生成问题.
EdDSA 签名算法由Bernstain 等人在2011 年提出.其计算中也有类似的公式:R=rB,S=(r+H(R,A,M)a)modL.秘密值a和秘密值r都需要采用秘密分享的方式进行保护.该算法联合计算需求包括单个秘密幂运算、两个秘密的加法.该算法同样也有随机数份额的安全生成问题.
根据上述对SM2、ECDSA 和EdDSA 算法的分析, 常用的联合计算方法包括以分享秘密为指数的幂计算、求两个分享秘密和的加法计算、求两个分享秘密乘积的乘法计算和求一个分享秘密倒数的求逆计算等.
2.4.2 联合幂计算
幂运算是公钥密码算法中的重要算法组件, 通常具有单向性, 例如RSA 中加密运算、椭圆曲线上的点乘运算等都是幂运算.幂运算的单向性指的是对给定x进行幂运算求得结果y是相对简单的, 而给定幂运算结果y求值x则是困难的, 其复杂性往往能归约到数学上的困难问题, 比如RSA 假设或离散对数问题.幂运算具有加法同态性, RSA 中memd=me+d, 椭圆曲线上aG+bG= (a+b)G, 也就是多个成员可以分别进行幂运算并公开各自的结果, 然后再进行合成求出最终结果.幂运算还满足乘法结合律, RSA中(me)d=med, 椭圆曲线上a(bG) = (ab)G, 也就是说多个成员可以按一定次序串行进行幂运算, 由最后一个成员输出总体计算结果.
在采用加性秘密分享的方案中, 从分享份额恢复秘密采用的是线性加法.根据幂运算的加法同态性,在进行分享秘密的幂运算时, 可以由每个参与方单独使用自己拥有的秘密份额进行幂运算并公开作为中间结果, 最后所有节点都可以收集并使用这些中间结果合成最终结果.例如, 考虑两个参与者的情况, 它们分别拥有秘密d的份额d1和d2, 并且d=αd1+βd2, 其中α和β是1 或者按照拉格朗日插值公式确定的常数.则在椭圆曲线上计算幂dG的时候, 可以由参与者1 计算并公开Q1=d1G, 参与者2 计算并公开Q2=d2G, 这样每个参与者都可以计算Q=αQ1+βQ2, 根据幂运算的性质, 可以看出Q=(αd1+βd2)G=dG.
在采用乘性秘密分享的方案中, 从分享份额恢复秘密采用的是简单的乘法, 根据幂运算满足乘法结合律, 在进行分享秘密的幂运算时, 可以由参与方按一定次序串行使用自己拥有的秘密份额进行幂运算并公开作为下一个参与方的输入, 最后一个计算的参与方输出最终结果.
2.4.3 联合加法计算
联合加法计算就是多个成员通过各自的分享ai和bi计算获得秘密a,b的和c的过程.
在采用加性秘密分享的方案中, 从分享份额恢复秘密采用的是线性加法, 根据加法的交换律和结合律,在计算分享秘密a和b的加法时, 可以由各个成员把自己拥有的份额ai和bi线性相加就得到了a+b的分享份额.例如, 在采用Shamir 秘密分享方法时, 考虑两个参与者的情况,a=αa1+βa2,b=αb1+βb2,其中α和β是1 或者按照拉格朗日插值公式确定的常数.则c=a+b= (αa1+βa2)+(αb1+βb2) =α(a1+b1)+β(a2+b2).可以看出只需要c1=a1+b1,c2=a2+b2, 也就是说将两个不同秘密的分享份额直接线性相加就得到两个秘密之和c的分享份额, 再根据拉格朗日插值公式计算出c.

如果要计算一个已分享秘密与一个常数(参与各方都知道的一个量) 的加法, 则计算结果是不能公开的.在采用多项式拆分的方案中, 相当于加上一个仅有常数项的多项式(次数为0), 也就是参与计算的成员简单地把各自的秘密份额都加上这个常数就可以了.而在采用简单加法拆分的方案中, 由于加法的结合律, 可以让参与计算的其中一个成员把自己的秘密份额加上这个常数就可以了.但是在乘性秘密分享的方案中, 计算一个已分享秘密与一个常数的加法仍然是一个较为复杂的问题, 一般不建议这么设计.
2.4.4 联合乘法计算
联合乘法计算就是多个成员通过各自分享的ai和bi计算获得秘密a,b的乘积c的过程.
在采用加性秘密分享的方案中, 从分享份额恢复秘密采用的是线性加法.考虑两个参与者的情况,a=αa1+βa2,b=αb1+βb2, 其中α和β是1 或者按照拉格朗日插值公式确定的常数.则c=ab=(αa1+βa2)(αb1+βb2)=α2a1b1+αβ(a1b2+a2b1)+β2a2b2.没有简单的方法在保密各自秘密份额的前提下计算c.已有的方案中, 常采用同态加密技术、不经意传输技术或Beaver 三元组乘法等完成加性秘密分享的乘法计算.两个秘密的乘积重新进行加性分享的方法被称为MtA (multiplicative-to-additive)方法.例如文献[14] 提出的MtA 方法, 为了完成乘积的秘密分享, 分享了若干个和为0 的秘密, 并在同态加密计算过程中消去, 从而得到秘密乘积的加性分享.此外, Shamir 多项式秘密分享方案作为一种特殊的加性秘密分享方案, 分享份额是分享多项式(t −1 阶) 的值, 而分享的秘密是这个多项式的常数项, 因此两个不同秘密的分享份额的乘积可以作为这两个分享秘密的乘积的分享份额, 只不过对应的分享多项式变为2t −2 阶, 需要2t −1 个成员才能通过插值公式恢复出共享的秘密, 这就需要总成员的个数n ≥2t −1.
在采用乘性秘密分享的方案中, 从分享份额恢复秘密采用的是简单的乘法,a=a1a2,b=b1b2, 因此c=ab= (a1a2)(b1b2) = (a1b1)(a2b2) =c1c2, 可以看出只需要c1=a1b1,c2=a2b2, 也就是说将两个不同秘密的分享份额直接相乘就得到两个秘密乘积的分享份额.
2.4.5 联合求逆计算
联合求逆计算也就是多个成员通过计算, 各自获得某个已分享秘密a的逆的分享份额的过程.假设成员Ui拥有秘密a的份额分别是ai, 通过联合求逆计算,Ui将获得c=a−1的分享份额ci.
在采用加性秘密分享方法的方案中, 通过如下步骤进行求逆计算: 参与计算的参与方通过秘密分享的方法分享新的随机秘密b, 参与方Ui的分享份额为bi; 每个参与方计算(ab)i=aibi并公开; 每个参与方通过秘密分享的恢复方法恢复出秘密ab, 并计算ci= (ab)−1bi得到a−1的分享份额.注意, 如果采用Shamir 秘密分享方法, 上述过程中需要至少2t −1 个成员参与计算.

2.5 门限密码方案评价指标
在实际部署中, 往往需要从不同的角度评价一个门限密码方案是否适合当前环境.本节中简单介绍一些评价的指标.
2.5.1 性能
密码学方案运算的性能是人们关注的要点之一.各类不同的密码方案需要在不同的性能与安全性之间做权衡.门限密码方案中, 主要关注以下几点:
(1) 是否需要交互.在门限密码方案中, 是否需要进行交互是一个重要的考虑因素.一般而言, 门限密码方案的执行过程中, 每个参与者需要进行运算并与其他参与者进行通信, 将自己的运算结果发送给他人, 也获取他人的运算结果.这样的交互显然会带来通信开销, 因此研究者们通过采用预处理方式, 减少交互次数, 更有学者提出了非交互式的门限密码方案[15–19].
(2) 方案执行轮次.门限密码方案需要多个参与者共同协作完成.把上面所说的所有人都进行发送-接收的过程称为“一轮”.在其他条件相近的情况下, 一个门限密码方案执行轮次越多, 那么需要的响应时间也越多, 门限密码方案也就越低效.
(3) 通信复杂度.通信复杂度与门限密码方案执行过程中, 所有参与者进行的数据交换总量有关.通信复杂度的计算包括部分解密/部分签名进行的数据交换, 以及通信中为了功能性额外附加的零知识证明等等.通信复杂度越高, 整体的门限密码方案执行效率越低.带宽指的是单位时间内传输的数据量, 研究者们也常用带宽(bindwidth) 一词来描述通信复杂度.
(4) 计算复杂度.计算复杂度关注的是各个参与者在门限密码方案中所需要进行的本地计算复杂度.计算复杂度除了考虑加密、解密或签名等操作本身的计算量外, 还可能会包括门限密码方案的零知识证明、同态加密等为了安全性、功能性进行的计算量.计算复杂度越大, 门限密码方案往往也就越低效.
2.5.2 安全性假设
不同的加解密、签名方案可能基于不同的安全性假设.例如, 基于大数分解的密码方案往往要基于RSA 问题的困难性, 而基于ECDSA 类算法的密码方案则一定会依赖于ECDLP 问题的困难性.早期的论文往往对方案安全性缺乏论证[20], 但是后来人们逐渐会对论文附上安全性的说明.为了可证安全, 很多方案引入了零知识证明或同态加密等技术, 这不但增加了计算量, 而且还引入了这些新技术的安全性假设,例如Paillier 同态加密算法基于复合剩余类的困难问题.
2.5.3 对敌手的假设
一个门限方案的敌手可能会在方案的执行过程中, 进行消息的多发、漏发、修改, 也可能会控制一个或多个门限方案的参与者, 掌握他们的秘密分享份额, 参与他们的门限方案执行过程, 并让这些被控制的参与者向其他参与者发送一些与方案正常执行时不同的消息.据此, 本文将从以下几个角度进行评判不同的门限密码方案中敌手的类型:
(1) 敌手在何时选取污染方.根据这一指标, 我们将敌手分为两类: 静态的和自适应的, 其中自适应敌
手会比静态敌手更难防御.
• 静态(static): 敌手必须在门限密码方案开始执行前就选定污染方.
• 自适应(adaptive): 敌手可以在任何时刻选定污染方, 包括门限密码方案开始执行前或执行过程中.敌手一旦选定了污染方, 就可以获得该参与者此前执行方案的所有计算过程, 并可以加以利用.
(2) 敌手是否遵循密码方案.在门限密码方案中, 不同类型的敌手在控制参与者后所采取的行动可能各不相同.基于其遵守门限密码方案规则的程度, 敌手可被划分为两类: 好奇的、恶意的, 其中恶意敌手会比好奇敌手更难防御.
• 好奇(curious)敌手: 也称为半诚实(semi-honest)敌手或被动(passive)敌手, 敌手会获取到污染方的计算过程等信息, 但不能强制被污染的参与者发送不遵循门限密码方案的消息.在这种情形下, 敌手能够读取并尝试利用污染方泄露的信息, 从而获取更多秘密信息.
• 恶意(malicious) 敌手: 也称为主动(active) 敌手, 敌手可以获取到污染方的信息, 同时也可以强制被污染的参与者发送不遵循门限密码方案的消息.在这种情形下, 敌手可以让污染方向其他门限密码方案的参与者发送任意消息, 并观察这些参与者的反应.
(3) 敌手能否控制信道.信道一般而言有两种, 即广播信道与点对点信道.当敌手控制并阻碍一些参与者之间的通信信道的时候, 可能会使得正常执行门限密码方案的参与方无法正常通信.为简化模型, 大多数论文会假设两种信道均可用且可信.
(4) 敌手是否有诚实多数假设.一些门限密码方案中会有“诚实多数” (honest majority) 的安全假设.也就是说, 这些密码系统仅考虑参与者有超过一半是诚实的情况, 即只针对满足n ≥2t −1 的(n,t) 构造门限方案.这样的假设可以简化方案的安全性证明, 然而, 实际场景很难强制敌手满足这一假设.一些门限密码方案[15,21–24]可以做到“非诚实多数” (dishonest majority), 即对任意满足n ≥t的(n,t) 都可以构造门限方案.
2.5.4 方案的特性
门限密码方案中还有一些值得探讨的特性:
(1) 是否需要可信方: 在门限密码方案中, 往往首先需要进行秘密份额分发.有的方案中, 这样的过程需要借助中心化的可信实体, 称之为可信方.一些方案为了提高效率、简化协议或完成安全性证明会引入可信方.然而, 引入可信方可能会带来单点故障的风险.
(2) 是否能够在异常情况下中止: 异常情况的处理是评估门限密码方案鲁棒性的关键部分之一.在多方参与者共同执行门限密码方案的情况下, 可能会出现部分参与者延迟响应、不响应或出现恶意行为的异常情况.诚实方如果在面对异常情况下仍无变化地继续执行原方案, 就可能会导致执行错误, 有些甚至会导致其秘密泄露[7,14,16,19,25–27].
(3) 同步或异步: 在门限密码方案中, 同步和异步描述了参与者之间的通信模式.对于一次通信而言,同步模型中存在着执行的先后顺序, 参与者需要按照指定的顺序完成计算操作, 而前面执行未完成时, 后面的必须等待.同步模型往往会让算法设计分析变得更加简单, 但是在实际应用中可能不太实用.异步模型中则不存在这样的时间限制, 参与者可以在任何时间接收或发送消息.
(4) 扩展性: 扩展性指的是随着参与者总量n的增加, 方案性能如何变化.随着参与者总量的增加,门限密码方案的通信量和计算量都可能会显著增加.扩展性良好的方案能够在大量参与者执行方案时也不会出现显著的性能下降.另一个值得注意的问题是一些方案可能仅考虑特定数量参与者设计, 如只考虑n=t=2 的协同签名情形.
3 算法与协议进展
门限密码学领域涵盖许多不同算法的门限方案研究.本节旨在介绍门限密码学在各类算法中安全性、效率等方面的研究重点和进展及在实践中的应用, 并让读者了解门限密码学研究的最新动态.
3.1 RSA 门限密码算法
RSA 算法是一种基于大数分解问题困难性构建的公钥算法, 也是目前世界上最常用的公钥加密和数字签名算法之一.研究者们对RSA 门限密码研究开展时间也相对较早, 近年来研究较少.RSA 算法密钥生成阶段需要随机产生两个大素数, 然后基于这两个大素数生成公钥和私钥.解密和签名阶段都是对私钥d进行幂运算.
RSA 签名算法相对比较简单, 研究者们对其门限计算做了许多研究.在1989 年, Frankel 提出了首个(n,n) 门限RSA 签名方案[28].该方案对私钥使用了加性秘密分享, 通过幂运算后简单相乘来计算完整的签名.1998 年, Rabin 等人提出了一个非诚实多数RSA 门限签名方案[29].该方案对私钥使用了加性秘密分享.在秘密分享阶段, 该方案同样需要可信第三方来预先确定RSA 参数, 私钥份额分享则是使用Feldman-VSS 协议[30].该方案中引入了可用的定期重新分享秘密的方法, 使该方案做到了主动安全(proactive), 增强了该方案的鲁棒性.Shoup 在2000 年提出了非交互性的非诚实多数RSA 门限签名方案[20].该方案借助可信第三方对私钥使用了多项式秘密分享, 通过扩展欧几里得算法, 可以结合各份额得到签名.该方案中, RSA 模数N=pq需要满足p、q为“强素数”, 即p= 2p′+1、q= 2q′+1 的p′、q′也需要是质数.2001 年, Damgård 等人提出了无需可信第三方进行密钥生成的RSA 门限签名方案[31].该方案对随机数模数中的p,q做了加性分享, 同时对密钥份额进行了多项式分享方法.同时该方案无需p,q为“强素数”, 只需要p −1,q −1 的最小质因子大于参与者数n即可.2006 年Almansa 等人则提出了自适应安全的RSA 门限签名方案[5].该文也假设具有可信第三方来帮助秘密份额分发, 并对私钥使用了特殊的加性秘密分享此外, 该文的私钥分享中还支持主动安全, 可以通过类似的方法[29]做到份额更新, 每次份额更新时公共私钥dpublic也会进行更新.该方案通过基于模拟的方法证明了其抗自适应攻击的安全性.2023 年, Tessaro 与Zhu 提出了一种能够满足TS-UF-1 安全性[15]的门限RSA 签名方案[8].该方案所述安全性中除了参与方数量n和需要合成完整签名所需的参与方数量t外, 还有一个参数k, 代表至多会有k个参与方会被污染.在这种安全性下, 必须要有足够多的诚实参与方参与, 才能生成一个签名.该方案设计了一个基于RSA 假设的线性哈希函数, 并用该哈希函数来代替FROST 方案[15]中的幂函数gx, 从而得到了一种依赖于RSA 假设的门限签名算法.
到Almansa 提出自适应安全的RSA 算法为止, 各类RSA 门限算法已经有了很好的表现, 如非交互性[20]、无需可信方[31]、自适应安全[5]等方面均有解决方案.在本世纪10 年代, 密码学的热点逐渐转移到了椭圆曲线等新兴算法中.此后对于RSA 门限密码算法的研究逐渐变少, 且研究范围主要集中在RSA模数的多方生成.表1 列举了若干具有代表性的RSA 门限密码方案.

表1 RSA 门限密码方案概要Table 1 Summary of threshold RSA schemes
3.2 ECDSA 门限密码算法
ECDSA 的门限密码研究可以追溯到其离散对数版本, 即DSA 签名的门限密码研究.然而早期的ECDSA (n,t) 门限签名均需要满足n ≥2t −1.也就是说, 这样的方案依赖于“诚实多数” 的假设.ECDSA 非诚实多数的门限密码方案直到2016 年才被Gennaro 等人提出[32].该方案在秘密份额分发的过程中假设有可信第三方能帮其完成秘密份额分享, 并在签名计算过程中使用了一种Paillier 同态加密算法的变种, 使其对(n,t) 的要求无需满足诚实多数.该方法对密钥和随机数使用了加性秘密分享, 通过加法同态加密方法完成了分享秘密的乘法计算和求逆计算, 为了安全性证明还使用了大量范围证明相关的零知识证明及承诺方法, 因此该门限密码方案的秘密分享算法计算量开销较大.
2018 年, Gennaro 和Goldfeder[14]对上述算法进行了优化, 引入Feldman 可验证秘密分享方法(verifiable secret sharing, VSS), 出现恶意敌手协议就会中止, 并在签名过程以轮次增加的代价大幅减少了计算量开销.同年, Lindell 也提出了类似的门限签名方案[33], 其秘密分享过程使用ElGamal 算法的指数形式代替了Paillier 算法, 减少了分布式密钥生成过程的计算量开销.2020 年, Gennaro 和Goldfeder在文献[14] 算法的基础上提出了一种ECDSA 门限签名方案[7], 改进了对协议中止情形的处理, 提供可识中止(identifiable abort), 并进一步提出了通过离线的预处理和将大部分计算交给本地计算的方法减少了交互轮次.
2019 年, Doerner 等人将其之前的协同签名方案[34]扩展为了普遍的(n,t) 门限签名方案[35].该签名方案对密钥使用了加性秘密分享, 同时对随机数k及其倒数k−1做了一种特殊的乘性秘密分享.该方法使用文献[36] 中所述的不经意传输(oblivious transfer, OT) 方法完成了分享秘密的乘法计算.由于其乘法计算是基于每两人进行一次计算这样的树状结构, 其交互轮次为对数级的.对于签名方案而言, 文中给出的结论交互轮次是为log(t)+6 轮.此外, 该文的安全性只需要依赖CDH 假设.
2020 年, Damgård 等人提出了一种使用Shamir 秘密分享的ECDSA 门限签名方案[25], 需要参与门限签名的(n,t) 保证诚实多数, 安全性仅依赖于ECDSA 的安全性假设.该门限签名方案的特殊之处在于使用了Shamir 算法代替了VSS 方案(verifiable secret sharing)进行密钥分发,使得其秘密份额分发效率得到了提高.文中还强调了之前一些基于非诚实多数的门限签名方案[14,33,34]没有做到公平性(fairness).也就是说, 敌手可以在自己生成完整的ECDSA 签名后中止协议, 这将可能导致其它诚实参与方获得不到完整的签名.该论文默认方案中也不保证公平性, 但是说明了如何在预处理阶段额外进行两轮计算来为该方案加入公平性.
2020 年, Canetti 等人提出了一种可识别中止、同时可以抗自适应攻击的ECDSA 门限签名方案[16].该方案对密钥和随机数使用了加性秘密分享, 通过MtA 的方法完成了分享秘密的乘法计算, 总体而言思路与文献[7] 类似.该方案的安全性在UC 框架(通用可组合性框架, universally composable[37]) 下进行证明, 其安全性可以归约到ECDSA 的不可伪造性、Paillier 加密和强RSA 假设的安全性上.该方案侧重关注各参与者的安全性, 组合了可识别中止以及抗自适应攻击两种特性, 使得在被污染的参与方发送恶意信息时, 该门限密码方案可识别出发送恶意信息的参与者, 并进行秘密份额的重新分配.同时, 该算法也将签名分为了未知待签名消息的预处理阶段与获取消息后的交互阶段.该方案中需要三轮预签名交互、一轮签名交互.该签名的三轮预签名方案对于可识别中止需要O(n2) 的计算才能得知发送恶意信息的是哪些参与方.该文还提出了一种需要六轮预签名加一轮签名的ECDSA 门限签名方案, 其安全性额外需要依赖于DDH 假设, 好处是识别出恶意参与方只需要O(n) 的计算量.
2020 年, Castagnos 等人在ECDSA 协同签名[38]的基础上, 提出了一种新的ECDSA 门限签名方案[39], 从而减少了计算量和带宽的开销.该方案对密钥和随机数使用了加性秘密分享, 通过MtA 的方法完成了分享秘密的乘法计算, 大体上的思路与文献[14] 类似.该方案的秘密分享阶段中, 将所使用的加法同态算法从文献[14] 中的Paillier 算法替换为了2015 年基于Castagnos 和Laguillaumie 提出的一种类群(class group) 的算法[40].使用Paillier 算法时, 消息空间依赖于大整数N, 这样会带来两个问题.一个问题是相对于较小的q, 这样的N导致消息空间过大, 因此计算量也会较多; 另一个问题是由于ECDSA的模数q往往是远小于N的(正如文献[32] 中提到N>q8), 这样一些算法中为了安全性, 需要对其中计算的值添加范围证明(range proof), 以确认计算所得值在N中较小的限定范围之内.该文指出, 与Paillier 算法不同, CL 同态加密算法的消息空间可以是Z/qZ, 当这里的q与ECDSA 签名中的大素数相同时, 该门限密码方案的消息空间使用效率变高.然而, CL 算法本身的计算需要基于类群, 当消息空间相同时, 其计算量远远超出Paillier 算法.因此, 该算法对于效率改进仍在一个数量级内.
2021 年, Kondi 等人[26]提出了一种能让(n,2) 门限方案从静态安全提升为主动安全的方法.该文所针对的方案需要使用Shamir 秘密分享或者是加性秘密分享, 且其签名方案使用随机数.文中指出, 主动安全方案大多数依赖诚实多数, 而且截至当时所有主动安全方案都需要每个参与者在预定时间在线, 这在实际应用中是难以保证的.该文提出的方法不依赖于在线的人必须诚实多数, 也不要求所有诚实方必须同时在线完成份额刷新.在性能方面, 该文在文献[14] 所提出算法的(n,2) 基础下进行了更新.在相同配置下需要14% 左右额外的性能开销将安全性提升为主动安全.
2022 年, Abram 等人[41]提出了一种具有预处理阶段, 且预处理阶段开销较低的全门限的ECDSA门限签名方案.该方案对密钥和随机数使用了加性秘密分享.在安全性上, 该方案依赖于环LPN 假设.该文假设在密钥生成中有可信第三方参与.该方案利用了2019 年Boyle 等人提出的一种利用不经意计算构造伪随机生成器的方法(PCG)[42].具体来说, 该文所述方案让门限密码计算的各个参与者可以在预处理阶段交互来获取一些相关的随机数, 也称作PCG seed.随后在参与计算的时候, 各个参与方可以利用本地的PCG seed 来产生可用于该方案的大量随机数, 从而节省了大量通信成本以及存储成本.与文献[39]类似, 该文也将大量计算放到了预签名阶段, 在预签名阶段需要两轮交互, 签名阶段只需要一轮简单交互.该方案一次签名运算时间总和比之前的工作[14,33,39]要慢一个数量级左右, 但是带宽成本则要低两到三个数量级.
2023 年,Xue 等人提出了一种新的ECDSA 门限签名方案[43].该文提出了使用JL 同态加密方案[44]来构造MtA 方案的思路, 并成功应用该思路构造了ECDSA 门限签名方案.使用JL 同态加密方案构造的MtA 方案能让消息空间比使用Paillier 的方案小,同时在承诺上的开销比基于CL 的方案小.该文构造MtA 的关键点在于对原始的JL 同态加密方案进行了修改, 使得密文与承诺之间的转换更加简单.基于强RSA 假设与k-QR 假设(JL 模数下的二次剩余假设) 证明了该MtA 方案的安全性.该文对一种ECDSA门限签名方案分别使用了基于Paillier、基于CL、基于OT, 与其提出的基于JL 方案构造的MtA 方法做了性能比较.从带宽来看, OT≫Paillier>JL>CL; 从计算量来看, CL>Paillier>JL≫OT.
ECDSA 的协同签名也是一个热门的研究方向.2016 年, Gennaro 等人提出了一个具有实际意义的ECDSA 协同签名算法[32]: 其应用场景为手机与电脑共同分享电子货币的支付密码.方案设计了手机端和电脑端的软件, 并使用二维码和TLS 进行通信, 协作完成签名算法, 进行电子货币支付.2017 年,Lindell 提出了一种快速的双方协同ECDSA 算法[45].该方案对密钥和随机数使用了乘性秘密分享, 借助具有加法同态的Paillier 方法完成了分享秘密的加法函数.该文设计了一种新的方案, 即U2具有U1私钥份额x1的Paillier 密文.该算法签名只需要四次交互, 且椭圆曲线运算也大大减少.该文指出文献[32]中每次签名每方需要计算1 次Paillier 加密、5 次Paillier 同态标量乘法、5 次Paillier 同态加法以及46次幂运算; 而该文中两方分别只需要7 次椭圆曲线乘法和1 次Paillier 解密以及5 次椭圆曲线乘法、1次Paillier 同态标量乘法和1 次Paillier 同态加法.从性能来看, 该文的实现在P-256 上平均一次秘密分享所花时间需要约2.4 秒, 而一次签名所花时间需要约36.8 毫秒.2018 年, Doerner 等人提出了一种ECDSA 协同签名方案[34].该方案对密钥使用了加性秘密分享, 对随机数使用了乘性秘密分享.该方案对不经意传输协议使用了一种新的扩展方法, 仅依赖于ECDSA 假设就实现了开销较低的协同签名.从性能来看, 该文的实现在P-256 上比文献[45] 的方案计算量要少70% 以上, 且平均一次秘密分享所花时间需要约43 毫秒, 而一次签名所花时间需要约3 毫秒, 大约都快了90% 以上.2019 年, Castagnos 等人提出了一种同样只需要四轮交互ECDSA 协同签名方案[38].该方案对密钥和随机数使用了乘性秘密分享, 借助具有全同态性质的CL 加密方法在文献[45] 的基础上进行改进, 完成了分享秘密的加法运算.同时, 该方案避免了使用Paillier-EC 这一非标准假设, 而是依赖于HSM 问题(hard subgroup membership).此外, 该方案的安全性依赖于哈希证明系统(hash proof system, HPS) 构建的零知识证明.从性能来看, 该文的实现在P-256 和P-384 上与文献[45] 方案的秘密分享、签名速率相当, 而在P-521 上则显著快(秘密分享约103 秒, 签名约1.8 秒; 而后者秘密分享约430 秒, 签名约2.4 秒).2021 年, Xue 等人提出了一种ECDSA 协同签名方案[46].该方案的核心思路是在签名的离线阶段进行一次密钥份额的“重分享”(re-sharing) 减少MtA 次数, 从而减少计算开销.在秘密分享阶段, 该方案对密钥使用了加性秘密分享.在签名的在线阶段, 该方案只需要进行一次交互即可完成签名.该文中还给出了该方案使用基于CL、基于Paillier、基于OT 几种不同的MtA 方法时的安全依赖与安全性证明.
表2 详细介绍近年来若干ECDSA 门限签名方案, 并列出其指标对比.其中安全性假设一列, 所有ECDSA 门限签名方案都自然依赖于ECDSA 签名方案的安全性, 因此不单独列出.

表2 ECDSA 门限密码方案概要Table 2 Summary of threshold ECDSA schemes
3.3 Schnorr 与EdDSA 类门限密码算法
EdDSA 签名算法[47]由Bernstein 等人在2011 年提出, 该算法是Schnorr 签名算法的变种.Schnorr 算法的安全性基于素数阶群上的离散对数问题, 而EdDSA 算法的安全性则是基于扭曲爱德华曲线Ed25519 或Ed448 上的离散对数问题.
相对于ECDSA 等算法而言, EdDSA 算法可以直接通过Shamir 等算法对私钥进行秘密分享从而实现门限算法, 其对应的门限算法实现起来较为容易.因此, EdDSA 被称为是门限友好的[48].值得注意的是, EdDSA 使用的随机数r除了通过确定性算法获取外, 也可以直接使用随机数生成器, 或是伪随机生成器进行概率性(probabilistic) 生成[48].
EdDSA 算法与Schnorr 算法的原理与计算过程相似.以下重点介绍几个常用的Schnorr 类算法.在这其中, 一些进展是针对Schnorr 算法本身性能的改进做出的; 而另一些则是对Schnorr 类算法做了安全性等方面的考量.
2021 年, Garillot 等人针对门限Schnorr 算法确定型随机数可能遭到的回滚攻击, 提出了一种无状态的随机数使用方案[49].该方案在非诚实多数的情形下可用, 对私钥和随机数使用了加性秘密分享, 主要考察的是确定性算法, 即类似EdDSA 式获取随机数的问题.具体而言, 每个参与者Ui会生成一个随机数密钥ki, 并在获取待签名消息的哈希值m后, 通过确定性算法计算随机数份额Fki(m) =ri.如文中所述, 单纯使用这样的方案而不加承诺可能会遭到文献[50] 中所提到的攻击, 即如果未事先确定这些随机数r可能值而敌手可以任取的话, 敌手可以污染一个参与方, 并请求与一诚实方对同一消息m取特定不同随机数r和r′进行门限签名, 并据此获得该诚实方私钥份额.这就需要对这些在门限方案中可能会用到的随机数进行承诺.然而这样的确定性算法往往是产生任意多随机数并用于门限签名的, 其数量并不确定,因此简单的承诺并不能直接奏效.为此, 该文提出了一种基于零知识混淆电路(ZKGC)[51]与不经意传输的承诺方案, 解决了这个问题.该方案使得对于门限Schnorr 方案而言, 参与方Ui可以在密钥生成期间对伪随机函数(PRF) 进行采样的ki进行承诺.在后续签名时其他参与方在计算Fki(x)·G=Ri时, 可以保证其使用的随机数是基于协议所述的确定性随机数方案所产生的.该文对这个方案所需要的附加计算量做了估计, 在128 bit 安全两方的条件下, 其总的带宽增加量约为每方1.01 MB.
2021 年, Komlo 与Goldberg 提出FROST 门限方案[6], 该方案对Schnorr 签名方案做了两轮交互非诚实多数门限.同时, 该方案也可以变形为带与消息无关的预处理方法的、需要可信第三方来进行签名交互的单轮交互门限签名方案.该方案的安全性均可以归约到随机预言机下的OMDL 假设[21].该方案对私钥使用了多项式秘密分享, 对随机数用了一种特殊的加性秘密分享.该方案随机数分享的特殊之处在于, 各参与者Ui将秘密份额ki分解为了ki=di+eiρi.其中参与者自行生成的随机数份额有两个, 即di和ei; 而这里的ρi为一个与i、消息m, 以及下文所提到的所有参与者随机数列表L相关.对密钥生成阶段而言, 该方案在Pedersen 的分布式密钥生成算法[52]基础上增加了对其第一轮分发时个人秘密的承诺, 用来防止非诚实多数情景下可能存在的rogue-key 攻击[53].文中同时指出秘密分享阶段可以借助Gennaro 式秘密分享方法[54]来获取鲁棒性, 但这额外需要诚实多数的条件.对一轮方案而言, 该方案的预处理方法是每个参与者Ui在每次签名前需要预先创建一个一次性的随机数列表Ui, 使得Li为对所有n ≥j ≥1 的随机数(dij,eij) 的承诺(Dij,Eij) 的集合.预处理阶段需要所有的Ui都将其随机数列表Li发给可信第三方.这里的随机数(dij,eij) 会在签名过程中用到, 由于各参与者已经预先做过承诺, 每一轮签名中所使用的随机数将无法被篡改.对两轮方案而言, 单纯将该方案预处理阶段发给可信第三方的Li广播到每一个参与者即可.
2022 年,Bellare 等人在FROST 算法[6]的基础上进行了改进,并提出了FROST2 算法[15].FROST算法与FROST2 算法均假设敌手为静态的, 且其安全性证明均归约到了随机预言机模型下的OMDL 假设, 这是比Schnorr 依赖的DL 问题要强的.该文对私钥使用了多项式秘密分享, 对随机数使用了特殊的加性秘密分享, 在方案上与文献[6] 是类似的.该方法的秘密分享过程还需要依赖代数群模型(algebraic group model, AGM) 下的DL 假设来证明Schnorr-KoE 假设, 从而做到非诚实多数情形下正常运行.在性能上, 该方案将一轮的FROST 方案中计算每个参与者Ui的哈希值ρi的方法做了改进, 降低了其门限签名中的乘方次数.此外, 该文对所有非交互门限签名方案及其安全性做出了定义, 对非交互门限签名方案提出了一类安全等级标准(TS-UF-0 到TS-UF-4), 并指出, FROST 是TS-UF-3 安全的, 而FROST2则是TS-UF-2 安全的.
2022 年, Lindell 提出了一种新型的交互门限Schnorr 算法[22].该文指出, 许多EdDSA 方法能在两轮交互中完成签名, 但是并不能在基于模拟的情境下证明安全性, 或者不能保证并发安全, 或者使用了非标准假设[6,15].该文安全性建立在随机预言机模型下的DL 假设下, 这是一种标准假设.该文对私钥和随机数使用了加性秘密分享, 在假设具有PKI 的情况下, 构造了一种能够保证并发安全的三轮协议.这里的PKI 体系保证了任何两方之间具有点对点的加密传输.文中指出, 虽然本协议需要使用零知识证明因而运行速度较慢, 但是在使用频率不高的情况下, 能够提高方案的安全性.
2022 年, Boneh 和Komlo 提出了一类新型的可追溯签名者的Schnorr 类门限签名算法[55].该文对私钥和随机数使用了加性秘密分享.该文指出, 截至当时的门限签名方案, 其匿名性要么是完全匿名无法追溯给出签名者的集合; 要么是可审计的(accountable), 即通过门限签名所有人都能够追溯到签名者的集合.该文关于Schnorr 签名提出了一种新的匿名性并进行了实现.具体来说, 该文方案只有拥有特定“追溯密钥” (tracing key) 的人才能知道签名者集合的信息.该文称这种签名为TAPS 签名(threshold,accountable, and private signature).该文通过安全性的理论分析找到了多种实现TAPS 签名的方法, 包括依赖zk-SNARK 方法[56], 或结合DDH 假设与可审计门限密码方案(ATS) 等.该文提出了两种效率较高的TAPS 实现方法, 分别是基于Σ 协议与Bullerproof 协议的.从复杂度来看, 两者验证复杂度均为O(n) 个群上的操作.方案实际性能取决于方案所用参数e: 后者形成的方案签名大小在n较大的情况下要小约e倍, 但是追溯时间则要慢约2e/2倍.
2022 年, Ruffing 等人提出了一种为Schnorr 类门限签名算法提供鲁棒性的方法[57].文中指出FROST[6]方案不具有鲁棒性, 即在诚实多数的情况下也不能保证只要存在t个诚实签名者, 就可以成功输出有效签名.一种朴素的为FROST 方案提供鲁棒性思路是对n名参与者中的每t名都执行一次FROST 方案的签名, 然而这样需要Ctn次, 开销太大.该文提出了ROAST (robust asynchronous threshold signatures) 方法, 至多只需要执行n −t+1 次FROST 方案的签名即可为其提供鲁棒性.该文将ROAST 应用到了FROST 方案中, 并提出了一种带可识别中止的Schnorr 门限签名方法, 称之为FROST3 方案.
2023 年, Tessaro 和Zhu 提出了一种通用的降低密码方案安全性依赖的方法[8].该文指出, FROST等安全性依赖于OMDL 假设的密码算法, 可以用线性哈希函数F来替代OMDL 假设中所用的指数函数x →gx, 从而将其安全性假设降低为依赖于AOMPR (algebraic one-more preimage resistance) 假设.进一步地, 该文证明了AOMPR 假设的安全性可归约到哈希函数的抗碰撞性, 从而说明了通过该文方案可对FROST 和FROST2 做修改, 使其安全性可归约到群上的线性哈希函数以及随机预言机下的离散对数假设.
2023 年, Crites 等人提出Sparkle 算法, 一种Schnorr 门限签名算法[23].该文对私钥使用了Shamir秘密分享, 对随机数使用了加性秘密分享.该文延续Lindell 的方法[22], 使用三轮交互保证了并发安全.该算法的安全性可归约到代数群模型及随机预言机模型下的AOMDL (algebraic one-more discrete logarithm assumption) 问题[58].同时, 该文在基于游戏的方法下证明了该方案的抗t个参与者污染的自适应安全.该文证明了其提出的方案在DL+ROM 下具有静态安全, 在AOMDL+ROM 下具有抗t/2 个参与者污染的自适应安全.
2023 年, Bacho 等人提出了Twinkle 算法, 一种Schnorr 门限签名算法[59].该文对私钥使用了Shamir 秘密分享, 对随机数使用了加性秘密分享.该文指出, Sparkle 算法基于OMDL 假设来应对自适应敌手带来的倒带攻击(rewinding).该文在Sparkle 算法上做出了改进, 在基于五步识别(five-move identification) 方法[60]基础上做到了抗自适应攻击, 从而减少了安全性的依赖.基于随机预言机下的DDH 假设, 用基于游戏的方法证明了其安全性.
2023 年, Garg 等人提出了一种新型的Schnorr 门限签名算法[61].该文定义了“无需设置的带权重门限签名” (weighted threshold signature without setup) 的(n,t) 方案.在这里, 无需设置指的是秘密分享阶段各参与方无需交互, 只需要独立生成密钥; 而带权重指的是各参与者Ui可以具有一定的权重wi, 使得当且仅当参与签名者的权重之和满足∑i∈Sign≥t方可完成门限签名.文中指出, 许多带权重签名的门限密码方案为了证明公钥聚合无误, 需要让各参与者发送公钥外的提示消息.该文提出了一种新型的FRI式多项式承诺方法替换了KZG 式的承诺方法, 以复杂度稍高的代价消除了对提示消息的依赖.从复杂度来看, 该方案的签名大小为O(log2n), 验证时间为O(log2n), 签名聚合时间为O(nlogn).以下表3 介绍了近年来若干具有代表性的Schnorr 和EdDSA 类门限密码方案.

表3 Schnorr 与EdDSA 类门限密码方案概要Table 3 Summary of threshold Schnorr and EdDSA schemes
3.4 SM2 门限密码算法
SM2 算法是我国自主研发的椭圆曲线公钥密码算法, 已被纳入国家密码标准GB/T 32918-2016 以及国际数字签名标准ISO/IEC 14888-3.SM2 算法包括加解密算法、签名算法等部分, 针对SM2 算法的研究主要集中在国内.
2014 年, 尚铭等人首次提出了SM2 门限解密方案与SM2 门限签名方案[2].在秘密分享方面, 该文对密钥和随机数都使用了Shamir 秘密分享方案.文中对是否存在可信第三方的情形进行了讨论.在门限签名过程要求签名参与方数量(n,t) 满足n ≥2t −1, 且需要有2t −1 个人参与签名.
2019 年, Zhang 等人提出了一种SM2 协同签名方案[62].在秘密分享方面, 该文对密钥和随机数使用了乘性秘密分享方案.该方案采用Paillier 同态加密和零知识证明技术完成了分享秘密的乘法计算.2020年, 冯琦等人提出了适用于移动互联网环境下的轻量级基于SM2 算法的协同签名算法[63].在秘密分享方面, 该文对密钥使用了乘性秘密分享方案, 随机数使用了的特殊秘密分享方案.该方案采用零知识证明完成了分享秘密的乘法计算.同在2020 年, 苏吟雪等人提出了一种适用于5G 环境下的物联网场景的基于SM2 算法的协同签名方案[13].在秘密分享方面, 该文对密钥使用了乘性秘密分享方案, 随机数使用了k=k1+d1k2的特殊秘密分享方案.从性能来看, 该方案不包含同态加密或者零知识证明的计算, 与文献[62] 相比计算复杂度小了很多.
2022 年, Han 等人提出了基于秘密共享的两方SM2 签名协议[64].该方案对密钥使用了乘性秘密分享方案, 随机数使用了特殊秘密分享方案.该方案引入了新的分享量, 利用乘法三元组(海狸乘法Beaver’s triple[65]) 高效计算秘密共享的乘法, 其计算成本较低, 且安全性能归约到标准的SM2 签名方案, 不过该方案需要7 个交互消息才能完成签名计算.
2023 年, Liang 等人提出了一种非交互式门限SM2 签名方案[19].该文对密钥和随机数使用了加性秘密分享方案.该方案在秘密分享过程中使用了Paillier 同态加密方法以及零知识证明方法确保安全, 并借助Gennaro 等人提出的MtA 方法[14]完成了秘密乘积的分享.该方案为非交互式, 只有最后一轮需要消息输入, 预签名过程需要两轮通信完成.该方案做到了非诚实多数, 允许任意n ≥t的(n,t) 方案.该方案在恶意多数下可以做到可识别的中止, 从而做到了抗自适应攻击.该文性能分析表明, 预签名过程的计算和通信成本随参与方数量线性增长, 仅为Canetti 等人门限ECDSA 方案所需成本[16]的1/3.
2023 年, 刘振亚等人对SM2 协同签名算法的计算框架做出了综述介绍[66].该综述将SM2 系统签名算法分为基于乘法密钥拆分、基于加法密钥拆分两大类进行介绍, 并就此展开了安全性和性能分析.
在产业化中, 协同签名作为门限签名的一种特殊形式, 得到了安全企业的广泛青睐, 在许多实际场景中已发挥作用.2014 年, 林璟锵等人提出适用于云计算的基于SM2 算法的签名及解密方法和系统的发明专利[12], 是最早提出的SM2 协同签名算法.该专利中对密钥使用了乘性秘密分享方案, 随机数使用了k=k1k3+k2特殊秘密分享方法.该专利主要针对通信双方分别存储部分私钥, 双方协作才能完成签名或解密操作的云计算场景, 缺少相应的安全性证明.后续又出现了很多SM2 协同签名相关的专利, 同样没有相应的安全性证明.2017 年, 袁峰等人提出了一种基于加法密钥分割的SM2 签名方法发明专利[67].该专利中对密钥和随机数都使用了加性秘密分享方案.该专利的秘密分享阶段使用了不经意传输方法, 利用双方生成的多个随机数共同生成了签名公钥.该方案虽然密钥生成阶段流程较多且需要很多随机数, 但签名阶段较为高效, 仅需要一次交互, 两个参与方都仅需要计算一次椭圆曲线点乘操作.2019 年, 韩留明等人提出了一种轻量级的基于SM2 算法的协同签名方法与装置发明专利[68].2021 年, 马昌社等人提出了一种SM2 协同签名方法发明专利[69], 这两个方案都对密钥使用了乘性秘密分享方案, 对随机数使用了特殊秘密分享方案.其中前者的拆分方式为k=d1k1+d1d2k2, 后者的拆分方式为k=k1+(1+d)k2.这两个方案密钥生成阶段、协同签名阶段两端各需要一个随机数、一次点乘, 算法计算效率较高.
3.5 双线性对门限密码算法
基于双线性对(bilinear pairings)的签名在密码学的短签名、基于身份的签名中有重要应用.2001 年,Boneh 和Franklin 首次提出了利用椭圆曲线上的双线性对构造基于身份的公钥加密算法[70](identity based encryption, IBE, 也称为标识密码).BLS 算法就是一种常见的基于双线性对的签名算法[70,71].我国自主研发的SM9 算法也是一种基于双线性对的标识密码方法.基于双线性对的签名算法具有较好的聚合性, 在许多场景能够应用.
2002 年, Boldyreva 首次提出了利用双线性对的门限签名方案[72].该方案可以构造出BLS 门限签名方案.该文对私钥使用了加性秘密分享, 并使用了Gennaro 式的密钥生成方法[54]进行秘密分享.2006年, Boneh 等人首次提出了一种双线性对门限解密方案[3].该文给出了从基于双线性对的门限IBE 方案构造门限解密方案的通用方案.该文给出的门限IBE 算法实例中对私钥使用了多项式秘密分享, 并且通过定期更新秘密分享份额实现主动安全.2014 年, Libert 等人提出了一种非交互式自适应安全的双线性对门限签名方案[17].该方案对私钥使用了多项式秘密分享, 依赖Groth-Sahai 证明系统[73]这一非交互式零知识证明工具, 证明了这种方案在标准模型下的自适应安全性.
2020 年, Tomescu 等人借助BLS 签名良好的可聚合性(使用拉格朗日插值公式计算), 构建了具有良好扩展性的BLS 门限签名方案[74].该文对私钥使用了多项式秘密分享, 并对秘密分享过程中所用KZG承诺方案[75]做了空间换时间的改变, 通过树状结构计算多个多项式的积, 并构造了AMT(authenticated multipoint evaluation tree) 证明方案, 大大减少了秘密分享所需时间.该文对承诺方案的使用方法做出了改进, 通过对多项式做承诺的方法, 能一次对多个值做承诺使得聚合的计算复杂度从O(t2) 降为O(t·log2(t)).
2020 年, Libert 与Yung 提出了一种具有鲁棒性的非交互式自适应CCA 安全门限解密通用架构[18],并在双线性群中进行了实例化.该文的双线性群签名门限方案对私钥使用了多项式秘密分享.该文在密钥生成过程中使用了CHK 范式[76]来做到非交互的CCA 安全.然而该文指出了使用CHK 范式的一个约束: 为了让各参与方确认私钥正确性, 会在密钥分发阶段根据公钥对密钥份额做承诺.这样的承诺会导致系统难以用基于模拟的方法证明抵抗自适应攻击的能力.为此, 该方案使用了哈希证明系统(hash proof system, HPS)[77]方法, 假设有一个模拟器知道所有私钥份额, 因此能够较好地进行抗自适应攻击的模拟.该方法会带来密文有效性问题, 即生成的密文并不能与明文公开可验证地进行关联.为此, 该方案在Groth-Sahai 证明系统[73]的基础上提出了一种新的哈希证明系统, 带有公开可验证的证明, 使得密文具有公开可验证有效性.
2021 年, Attema 等人提出了一种能显著降低签名大小的基于双线性对的门限签名方法[78].该文对私钥使用了多项式秘密分享, 还描述了对双线性群的非线性化部分如何使用Shamir 协议进行线性化.该文基于线性化技术, 将一种考虑线性关系的压缩Σ 协议理论[79]应用到了双线性电路中, 构造了一种能够减少通信开销的承诺方案, 比单纯使用Σ 协议零知识证明来做BLS 签名方案大约能减少三分之二的通信开销.
2022 年, Bacho 与Loss 对门限BLS 签名的自适应安全问题做了分析[80], 对私钥使用了多项式分享方法, 借助可信第三方以及随机预言机提出了一种分布式密钥生成方法.该文对BLS 的分布式密钥生成协议(DKG) 做了一种新的安全性定义, 借助AGM 模型[81]下的OMDL 假设说明了具有一致性、正确性以及预言机下的代数可模拟性(oracle-aided algebraic simulatability) 的DKG 方法可以达到自适应安全.另一方面, 该文证明了如果仅基于度为2 的OMDL 假设或者基于DL 假设是做不到自适应安全的.在这里, 一致性指的是即使有多达t个参与方被破坏, 所有诚实的参与方也会输出相同的公钥和公钥份额向量; 正确性指的是即使有多达t个参与方被破坏, 也存在一个多项式f, 使得所有参与方的私钥份额和公钥份额可以从这个多项式中计算出来, 并且公钥也可以正确计算; 预言机下的代数可模拟性指的是在OMDL 预言机的假设下存在一个模拟器Sim, 即使面对自适应的对手也能模拟诚实参与方在协议中的角色.
2023 年, Garg 等人提出了一种新的BLS 门限签名方案[82].秘密分享过程中, 该方案让各参与者Ui在本地生成公私钥份额si, 并广播公钥份额.由于秘密分享中无需通信, 该方案称这种门限签名为静默门限签名(silent threshold signatures, STS).文中指出, 静默门限签名可以在不修改公钥的前提下对不同消息m选择不同的门限值t.其要点在于该方案签名中一个n维{0,1} 向量b来标记谁参与了签名, 且bi= 1 当且仅当Ui参与该次签名.该方案对私钥使用了加性分享方法, 私钥值为私钥份额向量s与标记向量b之内积⟨s,b⟩= sk.文中指出由于各参与者的私钥份额都在本地自行计算, 为了安全性, 需要对//b//≥t以及⟨s,b⟩=sk 做承诺.该文借助了SNARK 方法, 对多项式编码的乘积做了拆分[83]从而完成了承诺.具体来说, 拆分方式是s(x)b(x)=sk+Qx(x)x+QZ(x)Z(x).从性能来看, 该BLS 门限签名算法针对参与者数目数量n= 1024, 秘密分享需要约46.3 秒; 针对门限值总量t= 1024, 签名聚合时间需要约470 毫秒.
2023 年, Das 等人利用BLS 签名构造了一种带权重的门限签名方案[84].该文指出, 传统的带权重门限签名往往需要根据各参与者需要的份额数量, 在秘密分享时分出足够多份额, 在一些场景需要较大的计算量.在秘密分享阶段, 该文借助有PKI 的假设完成了非交互的密钥生成.该方案参考了多方签名模式,即各参与者Ui在密钥生成中分别生成其私钥份额si并得到公钥份额pki=gsi, 同时各参与者具有权重wi.作为带权重的门限签名, 该方案最终形成的签名除了σ外, 还包含一个向量b来标记谁参与了签名,需要⟨w,b⟩ ≥t才能签名成功, 且签名公钥为⟨pk,b⟩= PK.该方案中, 如何对这两个内积结果做简短、计算量小的承诺是门限签名效率的关键.该文中借助代数群模型构造了一种特殊的SNARK 方法, 提升了门限签名方案的效率, 其安全性归约到代数群模型下的q-SDH (q-strong Diffie-Hellman) 假设.从性能来看, 该BLS 门限签名算法针对参与者数目数量n=4096, 秘密分享需要10.7 秒; 针对权重总量t=1024,签名聚合时间需要约22 毫秒.
3.6 格密码与门限密码
随着近年来量子计算理论与工程上的不断发展, 基于传统密码假设, 如离散对数假设及椭圆曲线离散对数假设的密码方案安全性受到了威胁.近几年研究者们致力于寻找基于其他困难问题的密码算法.格密码由于运算复杂度相对较低, 且签名大小相对较小, 被认为是一种合适的抗量子密码方案.基于格密码的公钥加解密与签名方案安全性主要基于SIS、LWE、MLWE、MSIS、NTRU 等问题的困难性.这些问题目前被认为在量子计算下仍是困难问题.
格密码的门限方案研究已经有十余年的历史.2010 年, Bendlin 和Damgård 提出了首个格密码门限解密方案[1].该文提出了Regev 解密方案[85]的门限版本, 其安全性可归约到LWE 问题.在秘密分享阶段, 对私钥向量及噪声向量的每个元素进行了Shamir 式加性秘密分享.该文中的分布式密钥生成方法思想来源于Cramer 等人提出的伪随机秘密分享方法[86], 需要对n个参与者中的t个参与者所构成的集合进行运算, 计算量较大.在安全性上, 该文指出其在多数诚实时抗好奇敌手, 并在n/3>t时抗恶意敌手.2013 年, Bendlin 等人提出了首个格密码的门限签名方案[87].该文所述方法构造了GPV 签名算法[88]的门限版本.GPV 算法基于Hash & Sign 范式[89]实现.Hash & Sign 范式指的是, 签名公钥为一个陷门函数f, 而签名私钥为其逆f−1, 对消息m签名时首先将m通过哈希方法H变换到f的值域, 然后输出签名σ=f−1(y), 验证方法为f(σ) =H(m).为确保安全性, 该文使用了强陷门函数[90].在安全性上,该方案在信息论上能做到自适应安全, 且在n/3>t时抗恶意敌手.该方案安全性依赖于GPV 方案的安全性.
2012 年, Asharov 等人[91]提出了一种新的门限解密方案构造思路.该文指出, 使用层次全同态加密(leveled FHE) 方案[92]可以有效构造(n,n) 门限全同态加密方案(threshold fully homomorphic encryption, TFHE), 从而构造(n,n) 多方安全计算方案.该文提出的门限解密方案构造方法中, 秘密分享阶段通过对门限解密算法的私钥和TFHE 使用的评估密钥进行加性秘密分享, 然后使用TFHE 方法对输入加密后进行多方安全计算.该文对BGV 同态加密方案[92]进行了门限化, 并据此构造了一种抗恶意敌手的门限解密方案, 其安全性依赖于LWE 假设与使用的零知识证明方法.
2016 年, Mukherjee 和Wichs 借助TFHE 方法与非交互零知识证明构造了一种两轮的(n,n) 门限解密方法[93].该文首先对GSW 全同态加密方案[94]进行了门限化, 使其成为使用多方全同态加密方案(multi-key FHE, MFHE).2018 年, Boneh 等人给出了(n,t) 门限全同态加密的定义, 说明了如何使用线性加分享方案和多项式秘密分享方案与全同态函数结合构造门限全同态方案, 并据此提出了用TFHE、带预处理的零知识证明系统(zero knowledge proof system with pre-processing, PZK) 将签名方案、解密方案门限化的通用解决方法(universal thresholdizer).在此基础上, 该文首次构造了格密码一轮交互的非诚实多数门限解密方案以及签名方案[24].
2019 年, Cozzo 与Smart 针对抗量子签名算法发表了一篇综述[95].文章指出, 大致可将现在较为成熟的抗量子签名算法分为四类: 基于格的、基于哈希的、基于MPC-in-the-Head 的和基于多变量的.该文对当时提交NIST 抗量子签名标准化的九种方案进行了算法分析, 总结了需要分享的秘密有哪些, 以及计算复杂度.根据该文分析, 假设不出现因敌手攻击而异常中止的情况, 基于格密码的几种方案签名所需时间较少, 且签名较小, 安全性是比较好证明的.同时, 格密码门限化时, 一些计算适合在有限域进行秘密分享, 另一些计算则更适合在二进制电路进行分享, 在二者之间进行切换的开销较大.
2021 年, Devevey 等人提出了一种两轮的非交互门限解密方案[4].文中提出的方案是对偶Regev 算法[88]的门限版本.该文在标准模型下证明其方案在诚实多数下具有鲁棒性, 且能够做到抗自适应攻击的CCA2 安全.其安全性依赖于DCR 假设(decision composite residuosity assumption)[96]与LWE 假设.在秘密分享中, 该方案的私钥为矩阵形式, 对私钥每一列和噪声各分量都使用了加性分享.该文基于游戏的方法证明了方案的安全性.
2022 年, Agrawal 等人提出了一种基于全同态加密的门限签名方案[97].该文对Boneh 的通用门限签名方案[24]做了改进, 使得需要全同态加密部分所需容纳的噪声上限大幅降低, 代价是该方案的签名大小与生成签名的个数相关.该文设计了Lyubashevsky 签名方案[98]无需中止的一个变种, 并给出了该变种的门限签名版本.该方案借助提供随机性的预处理方法, 在标准模型下实现了抗自适应攻击.
2023 年, Gur 等人提出了一种基于门限加法同态加密方案的两轮门限签名方案[99].该方案利用BGV 同态加密方案的门限版本以及零知识证明方法, 完成了非诚实多数下抗恶意敌手的门限签名方案.相较于之前使用全同态加密方案构造门限签名的方法, 该文指出可以将一些乘法步骤移出密文计算部分,从而减少同态加密所需开销.该文使用基于游戏的方法证明了方案的安全性, 对签名私钥、门限同态加密的私钥和噪声都使用了加性拆分方法.与文献[100] 不同, 该方案通过增加参数实现了两轮签名方法而无需中止, 提高了签名效率.从性能来看, 该方案的(5,3) 情形128 bit 安全时签名大小为11.5 KB, 公钥大小为13.6 KB, 参与方带宽各约为1.5 MB.
2023 年8 月, 美国国家标准技术研究院(NIST) 发布了两个有关格密码的标准草案[101,102].其中NIST FIPS 203 是格密码中的加密方案标准草案, 为KYBER 算法; NIST FIPS 204 是格密码中的签名方案标准草案, 为Dilithium 算法.目前研究者们对这些格密码方案已经有了初步的门限化研究.2020 年,Damgård 等人基于FSwA (Fiat–Shamir with aborts) 范式[100], 对Dilithium 方案的变种Dilithium-G,首次构建了DS3与DS2两种(n,n)的门限签名算法[103].这两种方案都对私钥及高斯分布生成的噪声进行了加性的秘密分享.其中前者需要经过三轮交互; 而后者只需要经过两轮交互, 是对前者的优化.两轮方案中, 为保证中止时秘密份额泄露不影响安全性, 在第一轮交互时传递的是对噪声份额的陷门承诺.2021年, Vakarjuk 等人基于FSwA 范式提出了首个(2,2) 的Dilithium 门限签名算法DiLizium[104].该方案对私钥及高斯分布生成的噪声都进行了加性的秘密分享.该算法实现了对Dilithium 提交的标准化版本的协同签名, 需要进行三轮交互.其安全性假设除依赖常见的MLWE、MSIS 假设外, 还依赖于非标准的Reject-MLWE 假设.2021 年, Laud 等人基于DiLizium 算法提出了DiLizium 2.0[105].该方案对私钥及高斯分布生成的噪声都进行了加性的秘密分享.该算法也是对Dilithium 提交的标准化版本的协同签名,同样需要三轮交互.但其安全性假设只基于MLWE 假设与MSIS 假设.以下表4 介绍了若干具有代表性的格密码门限方案.
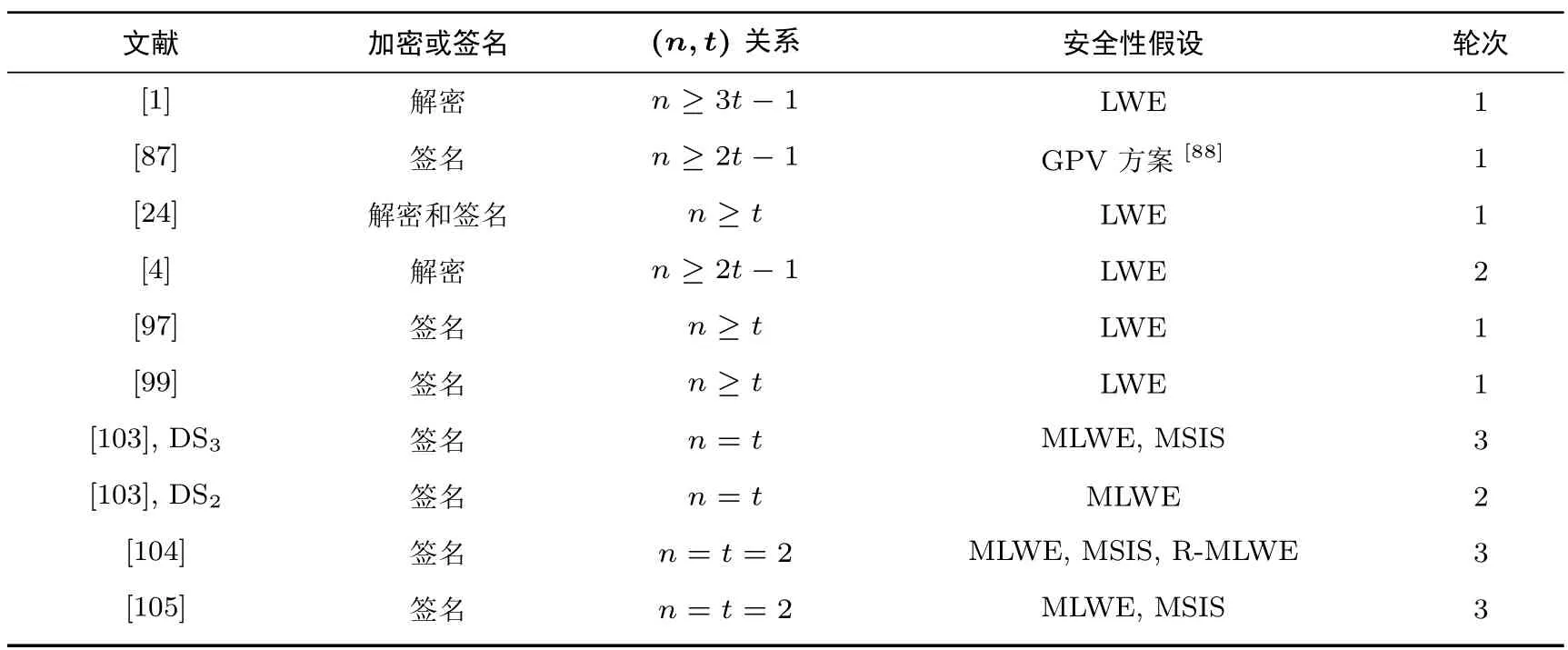
表4 格密码门限方案概要Table 4 Summary of threshold lattice-based schemes
4 应用及标准化进展
门限密码能够解决单点故障相关的漏洞.随着网络威胁变得越来越复杂, 使用门限密码是一个大的趋势, 对其标准化的研究也势在必行.在国际标准化方面, 密码领域的标准主要由国际标准化组织(ISO) 和国际电工委员会的信息技术联合技术委员会(JTC 1) 联合制定.我国各类密码标准则在国家密码管理局的领导和管理下稳步推进.目前(截至2023 年9 月) ISO 密码标准和我国密码标准体系中暂未发布对门限密码制定的标准.本文借他山之石, 向读者介绍其他两个标准化研究机构, 即NIST 与IETF 在门限密码相关领域标准化的进展.
4.1 门限密码的应用
门限密码方案, 包括门限解密和门限签名, 在各种现实场景中得到应用, 如区块链、云计算等.本节讨论门限密码可能的应用场景, 并对不同门限算法使用场景进行分析.
区块链: 门限密码方案能够做到去中心化, 因此在区块链等应用场景中能发挥很大作用.门限ECDSA 作为区块链中最早应用的密码方案之一, 是目前重点研究的密码算法之一[95].已有许多文献对门限ECDSA 在区块链中的应用进行了研究[32,106], 其应用场景主要是保护区块链交易的安全性.与ECDSA 签名不同, Schnorr 类签名如EdDSA 是门限友好的, 其门限版本所需额外开销较小, 因此许多区块链系统倾向于使用EdDSA 作为门限签名算法[50,107].基于双线性对的门限算法在运算人数较多时签名聚合效率较高, 也在区块链场景中获得了青睐[82,84,108].
云计算: 云计算中许多场景是客户端-服务器模式下运行的, 因此协同签名可以在该场景下得到充分应用[12,32,67,68,109].云计算中的边缘计算场景也可以应用门限方法, 研究者们指出可在车辆安全通信中[110]使用门限BLS 算法, 让车辆参与认证计算.研究者同时指出, 物联网中的设备在进行边缘计算时可以使用基于双线性对的门限环签名来保证匿名性[111].此外在生物认证中, 研究者指出可以在多设备间使用门限全同态方法[112]来加强安全性.
网络应用层安全: 网络应用层安全可以从应用门限 ECDSA 方案中受益, 在 DNS 运营安全(DNSSEC) 中应用门限ECDSA 方案[113]可以保护域名签名密钥的保密性, 同时保护DNS 服务器的真实性.
受信任执行环境: 受信任执行环境(TEE) 中, 可以应用门限ECDSA 方案来加强安全性[114], 其中的数据胶囊可以通过应用门限ECDSA 方案来加强访问控制.
总体而言, 门限版本的ECDSA、EdDSA 算法以及基于双线性对的算法都可以应用在区块链、物联网等场景中来加强系统安全性.目前门限格密码的研究还相对较少, 其使用所需时间空间代价都相对较高,应用场景也有待发掘.目前后量子密码算法标准化还正在进行中, 针对参选的各类密码算法已有关于门限版本可行性研究[95].相信在不久的将来, 门限格密码的应用也将成为现实.
4.2 NIST 门限密码标准化进展
截至目前, NIST 的多方门限密码工作组(multi-party threshold cryptography, MPTC) 已经组织了若干次讨论, 并发布了四份IR 文件.
2019 年, NIST 的计算机安全资源中心(CSRC) 团队发布了关于门限密码原语应当标准化的报告, 即NIST IR 8214 文件[115].该文件指出, 门限密码标准化是应当进行讨论的.这份文件主要讨论了两个话题, 一个是可以讨论标准化的思路, 如可以对门限类型、通信接口、执行环境目标计算与模型、设置与维护等方面进行标准化, 另一个则是建议讨论在何种粒度进行标准化.关于门限密码的研究目的, 该文件指出,门限密码会使用秘密分享方案来让密钥能分布在多方之间进行分享, 从而确保少部分密钥的泄露不会泄露完整密钥.门限密码中, 各方独立或者协作计算输出份额, 而不需要组合出完整的密钥.该文件指出可以考虑的点包括n个成员中最多容忍被污染(compromised) 数f和最少未被污染(uncompromised) 参与联合计算数k之间的关系, 如是否有k=f+1 或k=2f+1、是否有n>2f+1 或n>3f+1 等、是否需要可信方来进行秘密分享等操作.
从安全性方面考虑, 文中指出对门限密码而言有两类值得考虑的安全属性, 即可靠性(reliability) 和可用性(availability).在这里, 可靠性指的是安全目标不失败的概率, 而可用性指的是门限密码服务总体可用的时间或任务数比例.文件同时指出, 对门限密码安全性的证明也是很重要的.
从对门限密码方案的攻击方面考虑, 文中指出有若干类评价攻击方式的指标.第一种分类方式是根据攻击者是否只是获取协议执行相关信息, 还是会发送恶意消息或者进行其他恶意行为, 分为被动(passive)和主动(active).第二种分类方式是根据攻击者选择污染的参与方是否根据对于协议执行的观察进行, 分为不进行观察就直接选定污染方的静态(static) 以及可以根据观察协议执行情况而选择污染方的自适应(adaptive) 攻击.第三种分类方式是通过通信的接口进行攻击, 还是从执行时间、内存信息等处进行侧信道攻击.第四种分类方式是根据攻击是否能被探测(detectable) 到进行的, 不可探测的攻击可能会要求系统进行定期的备份.第五种分类方式是通过攻击者是否需要靠近门限密码系统的物理边界而分成需要接近的侵入性(invasive) 和不需要接近的非侵入性(non-invasive) 攻击.第六种分类方法是攻击针对的是门限化前的算法组件攻击(conventional) 还是对门限方案设计导致的漏洞(threshold-related).
从系统模型方面考虑, 可以有如下几个角度.第一个角度是交互(interaction).门限系统一般是n个节点之间进行交互, 同时也可能包括其他接口, 以及中继、代理等辅助组件.根据协议不同, 门限的性质可以选择是否将对外的接口公开或者进行隐藏.门限模型的交互性质还跟通信模型的定义, 如是否存在同步(synchrony)、可信信道(authentication) 以及信息传输是否进行了加密(encryption).此外可能有一些其他的可信组件, 如可信时钟会影响系统功能, 如解决异步通信的困难.第二个角度是身份信任问题.门限方案中可能有多种不同的设置, 比如由谁来决定执行多方门限方案的参与者, 各方的身份是否可以被其他各方所验证, 参与门限方案的成员是否固定或者是否允许新成员进入, 门限签名方案的实现是否要借助PKI 来进行等等.第三个角度是各客户端如何信任门限方案本身, 如客户端是否需要担心明文传输的机密性.如果需要保密的话, 客户端应该考虑是否需要使用可信代理、加密明文、进行秘密分享、使用特殊可信组件或者使用PKI 等方式进行消息传输.同时门限方案需要支持访问控制机制, 以确认哪些用户需要进行哪些加密操作请求.第四个角度是分布式协议与共识问题.文中指出有些系统具有脆弱性, 即在发生合理的环境变化情况下有灾难性故障, 比如一些从同步变成异步就会失败的系统.
从特征方面来看, 可以从门限类型, 即门限所容忍的f和k、是否同一方案在不同门限值的时候具有不同性质进行分类; 也可以从通信接口, 包括各客户端与门限方案的通信方式是通过广播还是秘密分享,各用户间的通信是否需要依靠一个中心节点还是直接可以两两通信, 信道是否有物理保护等方面进行分类.从目标执行平台来看, 有单台设备多芯片与多台设备等区分方法, 硬件执行与软件执行的区分方法.从设置与维护角度来看, 有份额生成是通过可信第三方还是安全多方计算生成的区分方法, 有参与人数固定和可增加的区分方法, 有不同访问控制的区分方法等等.
总体而言, NIST IR 8214 这份文件在较高的层面提出应当对门限密码做标准化工作.该文件指出, 可以在安全性、对密码方案的攻击、系统模型、特征、目标执行平台、设置与维护等方面进行标准化的考量.
NIST IR 8214A 文件最初是在2020 年发布了草案版本, 目前已经发布了最终版本[116].该文件对NIST IR 8214 文件中对门限密码标准化值得关心的分类进行了修改和细化说明.文件首先指出门限方案讨论的方位包括各类密码学原语(primitive), 尤其是核准算法.其中包括有数字签名(FIPS 186)、基于大整数分解(SP800- 56B) 或离散对数的密钥生成方法(SP800-56A)、随机位生成算法(SP800-90 系列) 等等.这份文件旨在为未来的标准化制定方法提供参考, 主要考虑NIST 核准算法.文件提出可以分单设备(single-device)、多方(multi-party) 两类对门限密码进行标准化工作的组织.在这两大类下, 对不同密码学原语, 如RSA 签名、RSA 解密、ECDSA 签名、EdDSA 签名等核准原语进行标准化.对每一种密码学原语, 可以分出若干不同的门限模式(threshold mode), 如通信是否进行输入、输出的秘密分享.实际的标准化过程会需要考察各类构建块元素、安全属性规范、监管需求、附加模块的可用性等等, 但是该文档认为首先需要关注原语和门限模式.密码原语层是门限方案标准化项目的重要组成部分, 原语主要包括签名、公钥解密、加解密、密钥生成、密钥协商几类.门限模式包括I/O 接口、互操作性、可审计性等方面的问题.总体而言, NIST IR 8214A 这份文件在较高的层面对NIST 门限密码标准化做出了指导, 指出标准化工作可以首先根据单设备、多设备分类, 接下来分别对不同的核准原语进行标准化, 再接下来针对不同的门限模式标准化.文件对单设备和多设备的区别、密码原语可能包括的种类以及门限模式定义做了较高层面说明.此外, 该文件还提到了安全性、监管需求等内容在标准化中也值得关注, 但并非该文件重点.
NIST IR 8214B 文件[48]为关于EdDSA/Schnorr 类签名的门限化标准建议, 该文件仍在公开草案阶段.承接NIST IR 8214 文件与NIST IR 8214A 两个文件的高层面讨论, 该文件对EdDSA/Schnorr类签名原语进行了讨论.该文件认为EdDSA 具有确定性算法, 是NIST 核准算法而且是门限友好的, 有很大的发展潜力.该文件总体上可以分为三个部分, 第一部分首先介绍了EdDSA 标准算法, 并延续NIST IR 8214A 文件介绍了与EdDSA 原始算法可互换(interchangeable) 的概念.第二部分介绍了EdDSA算法相关的门限方法, 指出密钥生成阶段可以分为中心化(有可信方) 和分布式生成两种, 在签名阶段, 该文指出可以将(n,n) 门限方案通过拉格朗日插值法转为(n,k) 门限方案.对于确定性门限Schnorr 类算法而言, 如果不能确认随机数的安全性(即确认随机数是由确定性算法产生的), 存在一种可以直接恢复密钥的攻击方法[50].这类问题可以通过混淆电路(garbled circuits) 等方法解决[117].关于概率算法的门限Schnorr 算法, 该文指出最近研究主要集中于减少交流轮次, 可以减少到一轮预计算加一轮签名, 比如文献[6] 的方案.第三部分主要在较高层面上讨论了门限方案可以关注哪些问题, 包括门限签名者、安全概念、系统模型、随机性以及模块化与可组合性.总体而言, 这是一篇分析EdDSA 签名方案与其门限方案的报告.该文件还对一些具体的门限方案进行了研究, 并分析了各类EdDSA 门限方案的特性及其优劣,如随机数生成中的确定性算法与概率算法之差别等.该文件对EdDSA 算法的研究进行了综合分析, 并针对性提出了对于现有方案可以展开的讨论, 为EdDSA 签名及其他密码学原语门限化打下了基础.
NIST IR 8214C 文件为2023 年发布的, NIST 对多方门限方案的初次征集, 截至目前(2023 年9 月)仍在公开草案阶段[118].这份文件旨在征集各类多方门限方案, 以支持NIST 制定未来的门限密码建议与指南.该文件所说的征集涵盖各类密码学原语, 包括NIST 核准原语(Cat1) 和具有良好性质的NIST 未核准原语(Cat2) 两类.从结构而言, 参与者提交的征集材料需要包含技术规范、参考实现、执行指令、实验评估和其他附加信息等五个方面的内容(M1–M5).从技术而言, 参与者提交的材料需要包含密码学原语、系统模型、安全理想化、敌手安全、门限配置文件和构建模块等六种技术内容(T1–T6), 在模块化描述中应该主要关注高级细节, 如接口和安全属性.总体而言, NIST IR 8214C 文件草案征集了包括NIST核准算法与非核准算法在内的各类门限密码方案, 并对参与征集的方案做出了理论和实现上的一些规范.NIST IR 8214C 文件预计会在2024 年发布最终版本, 并正式开始征集多方门限协议.
4.3 IETF 门限密码标准化进展
互联网工程任务组(Internet engineering task force, IETF) 是一个由全世界各地、互联网行业不同领域的参与者组成的开放社区.其声明文件[119]称, 该组织的目的在于制作高质量的技术和工程文档, 影响人们设计、使用和管理互联网的方式, 从而使互联网更好地运行.该组织撰写的文档包括互联网标准(STD)、当前最佳实践(BCP) 等, 往往通过RFC 文档(request for comments, 征求意见) 的形式发布在互联网上.
与NIST 不同, IETF 组织所写的文件可以说是自下而上, 由各个志愿者一同推动的.IETF 并没有特殊的准入门槛, 愿意为撰写文档做贡献的人都可以加入该组织.IETF 中的工作文档撰写可以由一名或多名IETF 成员创建网络草案(Internet-draft, I-D) 进行推动.网络草案被提出后, 会经过IETF 的工作组进行讨论.一个网络草案被工作组讨论同意后会移交到IRSG, 这相当于IETF 中的编辑审查委员会.当IRSG 同意之后, 这份草案就可能会变成RFC, 并保存在档案馆中.
门限密码相关的标准在IETF 中已经获得了关注, 但截至目前(2024 年1 月) 尚未出现已正式发表的RFC 文档.2021 年, Connolly 等人共同提出了一个关于FROST 构造的两轮门限签名方案标准[120], 目前已经获得IETF 密码学工作组的承认, 截至目前已经提交到了RFC Editor.该文档对Komlo 等人[6]在2020 年提出的FROST 方案两轮门限签名方案做了详细的定义.FROST 方案是一种生成Schnorr 签名的两轮门限方案.该标准对于FROST 两轮门限签名做了密码学依赖、辅助方法、方案内容、参数定义、安全考虑等方面的规范性说明.
总体而言, IETF 这份关于FROST 门限签名方案的标准化草案, 对FROST 方案进行了各层面的定义和介绍.在接口层面, 该文件对FROST 方案的签名部分进行详细的描述, 但是没有对密钥生成过程进行定义.在安全性分析方面, 该文件所述FROST 方案安全性主要依赖于已有文档的介绍(实际上, 该文件本身没有进行详述), 并做了简单的附加说明.在配置参数方面, 该文件对FROST 方案所用群与哈希方法进行了规定, 并说明了群(椭圆曲线) 参数与哈希相关内容.与NIST IR 8214C 不同, 该文件没有给出软件方面的实例, 也没有实际测试其性能.但是该文件给出了若干使用FROST 方案的KAT 集.该文件为门限密码标准化给出了一个好的开始.
4.4 标准化方向
门限密码标准化是一个漫长而严谨的过程.门限密码标准化所关注的内容范围很广, 包括了门限密码与客户端I/O 交互方式与接口、门限密码内部的系统模型(交互信道、各参与者之间的信任问题等)、门限类型(如参与者n与容忍门限t之间的关系)、方案考虑的敌手情况、安全性分析、具体实现场景是单设备还是多设备、所使用的密码学原语种类等方面.但是从实际来看, 这些值得关注的各个方面需要逐步推进.从门限密码标准化实际征集的内容来看, 门限密码标准化也很需要考察在实际应用场景中是否适用.NIST IR 8214C 征集的方案要求对具体的方案做软件实现, 并在一定的平台(benchmark) 上对其性能进行评估.同时除了有完整的理论模型安全性分析之外, 还需要分析理论模型中的一些组件替换为实际组件后是否会带来安全风险.
从门限密码的标准化原语来看, 国际上的门限密码标准关注的主要是国际最常用的算法, 如EdDSA算法等.NIST IR 8214C 所提出的是否首先要进行标准化的考量原因之一是NIST 是否核准.我国门限密码的标准化进程除了关注这些算法之外, 还同样应该关注密码标准体系中的算法, 例如SM2 数字签名算法等.推动门限密码标准化是密码学发展的必然趋势.
5 总结与展望
本节对前文所述研究现状及标准化进程进行总结, 并对未来研究可能的几个重点方向进行展望.
5.1 门限密码研究现状与展望
近年来, 门限密码学已从一个学术性的研究领域逐渐转变为实际应用的关键技术.随着分布式系统、云计算和区块链等技术的兴起, 门限密码由于具有较强的容侵能力, 其重要性正日益凸显.研究者们已经提出了许多创新的门限密码方案, 涵盖了各种密码学原语, 如RSA、SM2、格密码算法.随着安全需求的提升, 门限密码技术的标准化得到了众多发达国家的重视, 美国国家标准技术研究院(NIST) 和互联网工程任务组(IETF) 等机构在密码门限化的标准化相关工作中是非常典型的.
从算法原语上看, 随着各类算法原语向后量子方向迁移, 门限格密码必然成为门限密码中的热点.目前门限格密码的通用方案往往要依赖于全同态加密这一开销巨大的组件, 因此不能做到完全实用.从方案设计来看, 各参与方需要保证秘密不泄露的同时能够进行联合计算.为此, 研究者们使用不经意传输或各类不同的同态加密方案等方法, 其中近年来研究者们指出相较于较早常用的Paillier 方案而言, JL 同态加密方案[44]与CL 同态加密方案[40]能够在许多场景下开销更优.在安全性的归约方面, 近年来研究者们提出的AOMDL 假设与AGM 模型, 能通过代数结构为方案设计者提供新的归约思路.目前各类门限密码方案层出不穷, 已有在轮次上最优或性能上较优的算法, 少有各类场景下都表现很好的最优解, 亟待研究者们继续完善.
尽管普遍的(n,t) 门限密码学已取得显著进展, 门限密码标准工作推进也很快, 但产业跟进却非常迟缓, 复杂的协议设计和较低的计算效率仍然制约着门限密码的应用.门限密码的设计仍然存在许多待解决的挑战和问题.例如, 如何在保证安全性的同时提高效率、如何针对性构造门限密码方案满足不同场景的需求等等.特别是, 多个设备带来的高成本仍旧是当前的一个重要问题.相较之下, 较为简单的(2,2) 门限签名方案, 也就是协同签名方案, 在业界得到了较为成熟的应用, 为软件密码产品提供了可靠的安全保障.
5.2 门限密码与现实世界
随着电子信息技术不断进步, 密码技术与工业产业结合是一个大的发展趋势.目前国际上尚未有正式的门限密码标准公布, 我们可以积极参与标准化过程, 制定国内的门限密码标准, 确保我们的技术和应用得到充分的考虑.
目前协同签名已经在许多领域有了广泛的应用, 如已有利用协同签名技术部署云交易服务的平台, 保证密钥安全和信息传输安全; 电子签章系统行业市场在2022 年已达百亿规模, 已经出现利用协同签名技术开发的手机电子签名APP.信息安全行业的许多问题迫切需要新技术带来的解决方案, 而这都需要我们一步一步去实现.
