对称密码的量子分析法综述*

董晓阳

1.清华大学 网络科学与网络空间研究院, 北京 100084

2.密码科学技术国家重点实验室, 北京 100878

3.山东区块链研究院, 济南 250102

4.中关村实验室, 北京 100194

1 引言

1994 年, Shor 的开创性工作[1]表明, 规模足够大的量子计算机能够在多项式时间内对大整数进行因子分解和求解离散对数问题, 这将会破坏当今广泛使用的许多公钥方案, 如RSA 和ECC 等.为了迎接未来的挑战, 公钥密码学界和标准化组织投入了大量精力进行后量子公钥密码方案的研究.特别地, 美国国家标准与技术研究院(National Institute of Standards and Technology, NIST) 在2016 年启动了后量子标准征集竞赛(Post-Quantum Cryptography Standardization), 旨在征求、评估和标准化一个或多个抗量子公钥密码算法[2].相比之下, 关于量子计算如何改变对称密码的安全格局的研究似乎不太活跃.1996年, Grover 算法[3]的提出使得穷举搜索攻击在量子计算环境下能够获得二次加速(quadratic speedup),即在N个元素中找到某一特定元素, 经典计算环境下所需的时间复杂度平均为O(N/2), 而在量子计算环境下, Grover 算法能够在O(√N) 的时间复杂度下找到该元素.在十余年的时间里(1996–2010 年前后),密码研究者普遍认为, Grover 算法是对称密码的唯一量子计算攻击威胁, 因此密码研究者认为加倍密钥长度即可解决该问题[4].2010 年和2012 年, 随着Kuwakado 和Morii 的初步工作, 这种观点开始发生变化.他们证明了经典计算环境下可证明安全的Even-Mansour 密码和三轮Feistel 网络可以在量子计算机的帮助下在多项式时间内被破解[5,6].在2016 年美密会上, 法国密码研究者Kaplan 等人[7]利用量子计算模型进一步在多项式时间内破解了广泛使用的认证和认证加密模式, 如CBC-MAC、PMAC、GMAC、GCM 和OCB 等.这些具有指数加速(由指数级别的时间复杂度降低至多项式级别时间复杂度) 的量子计算攻击都是利用Simon 算法[8]来寻找依赖密钥的隐藏周期, 过程中需要以量子叠加态访问用量子线路实现的密码算法, 这是一个比较强的攻击条件.而以经典的方式收集明密文对, 并利用离线的量子计算机进行密码攻击成为相对实际的攻击假设.另外, 在量子计算模型中, 不同于经典随机存储, 量子随机存储被广泛认为是难以高效构造的[9,10], 因此使用更少的量子随机存储是优化量子攻击的重要方向.本文综述了分组密码和典型结构、认证和认证加密算法以及哈希函数等在不同攻击条件下的重要量子计算分析进展,部分参考了眭晗等人2020 年的综述论文[11]以及梁敏等人2021 年的综述论文[12].

2 量子计算与基本算法

2.1 量子比特和运算

值得注意的是, 如果函数f能够在经典电路模型下快速实现, 那么其对应的量子酉变换Uf亦能够在量子线路模型下快速实现.

2.2 Grover 算法

2.3 量子振幅放大算法QAA

通俗来讲, 假设要寻找集合X中被标记的元素, 这些被标记的元素构成集合M ⊂X, 且已知ϵ=|M|/|X|.显然经典搜索算法需要O(1/ϵ) 时间复杂度.确定量子Grover 算法的复杂度, 需要确定下列两个运算的复杂度, 即Setup 运算和Checking 运算:

量子振幅放大算法(quantum amplitude amplification, QAA) 是Brassard 等人[13]提出的.该算法可以被视为Grover 算法的一般化.简单来说, 假设存在量子算法A来生成集合X中“好” 的元素和“坏” 的元素的量子均匀叠加态, 同时, 令a是测量初始状态A|0产生“好” 的元素的成功率.假设B能够区分量子算法A的输出是“好” 元素还是“坏” 元素, 那么量子振幅放大算法可以以下时间复杂度找到“好” 的元素:

2.4 Simon 算法

给定一个函数f:{0,1}n{0,1}n, 它在某个n比特周期a异或下保持不变, 即存在0, 使得对任意的x ∈Fn2,f(x) =f(x ⊕a).那么问题是找到这个周期a.在经典计算环境下, 解决该问题的最优时间复杂度约为2n/2.然而, Simon 在1997 年提出量子Simon 算法[8], 能够以多项式时间量子复杂度找到该周期a.Simon 算法的步骤如下:

这是因为对任意的x ∈Fn2,f(x) =f(x ⊕a).因此当测量第二个状态的时候, 假设其坍缩到状态t, 其一定对应某个z, 使得f(z)=f(z+a)=t.因此第一个寄存器将坍缩成两个状态的叠加, 即

(4) 在上述寄存器上使用Hadamard 变换, 得到:

(5) 当y·a=1 时,|的振幅为0.因此测量上述叠加态得到的y总满足线性方程y·a=0.

重复上述步骤O(n) 次, 可获得足够多的关于a的线性方程, 求解该方程, 可获得周期a.

3 分组密码和及其工作模式的量子分析

2012 年, Zhandry[14]提出了两种量子计算模型, 分别描述了不同的量子攻击条件:

• 标准安全模型(Q1): 攻击者可以访问量子计算机来执行任何离线计算, 但只允许他们以经典方式进行在线访问密码算法.即, 敌手只能以经典方式收集明密文对等数据, 然后利用离线的量子计算机进行密码分析.

• 量子安全模型(Q2): 攻击者可以直接以输入的量子叠加态访问密码算法的量子线路实现, 并得到处于量子叠加态的输出, 同时也具备Q1 模型的攻击能力.

本文分别总结了两种攻击条件下的量子分析成果, 记为Q2 型攻击和Q1 型攻击.

3.1 Q2 型攻击

Q2 型攻击即攻击者可以直接以输入的量子叠加态访问密码算法, 并获得处于叠加态的输出.Kuwakado 和Morii 在2010 年和2012 年发现了经典计算模型中被证明安全的密码结构在量子Q2 模型下存在多项式时间的量子区分攻击[5,6], 即3 轮Feistel 结构和Even-Mansour 结构.这些攻击是利用密码结构特点构造周期函数, 而秘密信息则隐藏在秘密的周期中.利用量子Simon 算法, 这些秘密的周期能够在量子多项式时间被恢复, 从而达到攻击密码的目的.随后, 在2016 年美密会上, Kaplan 等人利用量子Simon 算法攻击攻击了一系列认证和认证加密算法[7], 包括CBC-MAC、PMAC、GMAC、GCM、OCB, 以及CAESAR 竞赛候选算法CLOC、AEZ、COPA、OTR、POET、OMD 和Minalpher.在2017 年亚密会上, Leander 和May 将Simon 算法和Grover 算法相结合(Grover-meet-Simon), 给出了FX 结构的量子密钥恢复攻击[15].

3.1.1 Feistel 等分组密码结构的量子分析

在CT-RSA 2019 上, Ito 等人[16]提出了4 轮Feistel 的量子选择密文区分攻击(quantum chosenciphertext attack, qCCA).Dong 等人研究了Feistel 和广义Feistel 的一系列量子多项时间区分攻击, 并结合Grover-meet-Simon 算法给出密钥恢复攻击[17–19].针对Feistel 的量子分析引发了学术界对多种密码结构展开分析, Cui 等人研究了MISTY L/R、CAST256-like、CLEFIA-like 等典型Feistel 结构的量子攻击[20].Cid 等人给出了7 轮SM4 的量子区分攻击以及相关密钥下的量子攻击[21].Hodz̆ić 等人研究了Type-3 型广义Feistel 和SM4 的量子攻击[22,23].邹剑等人将Simon 算法的周期性质与生日攻击思想相结合, 提出了一种新型传统密钥恢复攻击[24].罗宜元等人研究了对MISTY L/R 和Lai-Massey 的量子分析[25].Mao 等人[26]研究了Lai-Massey 结构的量子选择明文和量子选择密文区分器.Zhang 等人给出了Type-3 型广义Feistel、带膨胀论函数的非平衡Feistel、以及Lai-Massey 结构的量子攻击[27,28].Gouget 等人研究了MISTY 结构的量子分析, 并证明了3 轮MISTY R 的抗选择明文攻击(chosen-plaintext attack, CPA) 的安全性[29].在2022 年美密会上, Canale 等人提出了自动化地应用Simon 算法的工具[30], 并给出了MISTY L-FK 和Feistel-FK 分析.

3.1.2 认证和认证加密算法的量子分析方面

在学术界发现多种认证和认证加密算法存在量子攻击[7,31]之后, 密码学者开始对认证和认证加密算法的抗量子攻击能力进行了更深入的研究.在SAC 2017 上, Bonnetain 给出了CAESAR 认证加密竞赛候选算法AEZ 量子密钥恢复攻击[32].Shi 等人发现了AEZ-PRF 的碰撞攻击, 基于量子Simon 算法可以构造该算法的伪造攻击[33].在2021 年亚密会上, Bonnetain 等人提出了量子线性化攻击(quantum linearization attack)[34], 该方法可以基于Simon 算法[8]、Deutsch 算法[35,36]、Bernstein-Vazirani 算法[37]、以及Shor 算法[1]等多种量子算法构造量子攻击.基于量子线性化攻击, Bonnetain 等人给出了多种并行MAC 的量子攻击, 包括LightMac、PMAC 以及多种具备超越生日安全界的MAC (beyondbirthday-bound MAC, BBB MAC), 如LightMAC+、PMAC+, 以及ZMAC、PolyMAC 等[34].在PQCrypto 2021 上, Guo 等人针对12 种BBB MAC 的抗量子攻击安全性进行了系统性的研究[38].随后, Sun 等人给出了BBB MAC 的新型量子攻击[39].2022 年, Guo 等人针对基于公开置换的伪随机函数给出了一些列量子攻击[40].

3.1.3 经典分析方法的量子化(Q2 模型)

2016 年, Kaplan 等人[7]给出了经典滑动攻击(slide attack)[41]的量子化版本, 并取得了指数级加速.针对高级滑动攻击[42], Bonnetain 等人[43]和Dong 等人[44]分别独立地提出了量子化版本, 给出了2K-/4K-Feistel 等算法的量子攻击.针对俄罗斯标准GOST 分组密码, 董晓阳等人提出了经典的反射攻击(reflection attack) 和不动点攻击(fixed point attack) 的量子化版本[44], 给出该算法全轮的量子密钥恢复攻击.2019 年, Xie 和Yang 利用Bernstein–Vazirani 算法[37]研究了分组密码的差分分析和不可能差分分析[45].Cai 等人结合量子BHT 算法[46]和滑动攻击, 给出了1K-AES 和PRINCE 分组密码的量子密钥恢复攻击[47].Chen 等人提出了搜索不可能差分和零相关区分器的量子算法[48].David 等人提出了SKINNY 和AES-192/-256 的量子不可能差分攻击[49].Frixons 等人[50]和Zou 等人[51]研究了量子飞去来器攻击.Hosoyamada 提出了量子多维(零相关) 线性和积分攻击[52].随后, Schrottenloher 在Q1 和Q2 模型下提出了基于量子傅里叶变换的量子线性攻击[53].

3.2 Q1 型攻击

在Q1 量子安全模型下, 攻击者只需要通过经典的方式收集明密文对, 然后利用离线的量子计算机对密码进行分析.因此,相对于Q2 量子安全模型,Q1 模型对攻击前提假设比较弱,因此攻击更加实际.除了Q2 模型下的多项式时间量子攻击, Kuwakado 和Morii[6]针对Even-Mansour (EM) 密码亦提出了Q1模型下利用BHT 算法的量子攻击, 其所需的经典查询、量子计算复杂度和量子比特数量均为O(2n/3).在CT-RSA 2018 上, Hosoyamada 和Sasaki[54]将EM 结构的Q1 型攻击所需的量子比特数目降低为多项式级别, 但是所需的经典查询和量子计算复杂度升高至O(23n/7).同时, 他们给出了多种MAC 算法的Q1 型攻击, 如Chaskey、McOE-X 等.在2019 年亚密会上, Bonnetain 等人针对EM 结构、FX 结构等提出了离线的Simon 算法[55], 并在TCHES2022 上给出了具体的量子实现[56].在2022 年欧密会上,Bonnetain 等人给出第一个在仅使用经典查询的情况下, 相比于最佳经典攻击实现二次方加速的量子Q1型攻击[57].

在经典分析法的量子化方面, Kaplan 等人[58]在2016 年提出了量子差分分析和量子线性分析.2018年, Hosoyamada 给出了6 轮Feistel 结构的量子Demiric-Selçuk (DS) 中间相遇攻击[59].随后, Bonnetain 等人针对AES 提出了量子Square 攻击和DS 中间相遇攻击[60].Naya-Plasencia 等人提出Q1模型下的飞去来器攻击[50]和不可能差分攻击[49].

4 哈希函数的量子分析

密码哈希函数H可以将一个任意比特长度的消息M压缩成n比特固定长度的摘要T.给定一个初始向量IV, 一个安全的哈希函数在经典计算环境下应满足以下三个基本安全属性:

• 抗原像攻击属性(preimage resistance): 对于给定的摘要T, 寻找到消息M, 使得H(IV,M)=T,所需的时间复杂度应不低于O(2n).

• 抗碰撞攻击属性(collision resistance): 寻找两个消息(M1,M2), 使得H(IV,M1)=H(IV,M2), 所需的时间复杂度应不低于O(2n/2).

• 抗第二原像攻击属性(2nd-preimage resistance): 给定消息M, 寻找另外一个消息M′, 使得H(IV,M′)=H(IV,M), 所需的时间复杂度应不低于O(2n).

在量子计算环境下, 可以利用Grover 算法[3]寻找哈希函数的原像和第二原像, 所需的时间复杂度是O(2n/2).针对碰撞攻击, 学术界又分为以下三类:

• 标准碰撞攻击(collision attack): 找到两个消息(M1,M2), 满足H(IV,M1)=H(IV,M2).

• 半自由起始碰撞攻击(semi-free-start collision attack): 找到两个消息(M1,M2) 和IV, 满足H(u,M1)=H(u,M2).

• 自由起始碰撞攻击(free-start collision attack): 找到两个消息(M1,M2)、v和v′, 且′, 满足H(v,M1)=H(v′,M2).

针对碰撞攻击, 由于不同的攻击假设或条件下, 量子碰撞攻击所需的资源和时间复杂度不同, 需要分类讨论.

4.1 通用量子碰撞攻击

4.1.1 需要大规模量子存储的量子碰撞攻击算法

1998 年, Brassard、Høyer 和Tapp 提出了BHT 算法[46], 能够在O(2n/3) 时间复杂度和O(2n/3)规模的量子存储(quantum random access memory, qRAM) 复杂度下找到碰撞.这里量子存储qRAM是经典存储RAM 的量子形态, 其能够以量子叠加态高效地被访问.假设L= (x0,x1,···,x2m−1), 其中xi ∈Fn2(i= 0,1,···,2m −1).那么, 存储L的量子存储qRAM 进行如下酉变换操作, 定于酉变换UqRAM(L) 为:

其中i ∈Fm2为访问的地址,xi ∈Fn2为地址i上存储的数据.因此我们能够以处于量子叠加态的地址访问L, 并获得相应地址上的数据的量子叠加态:

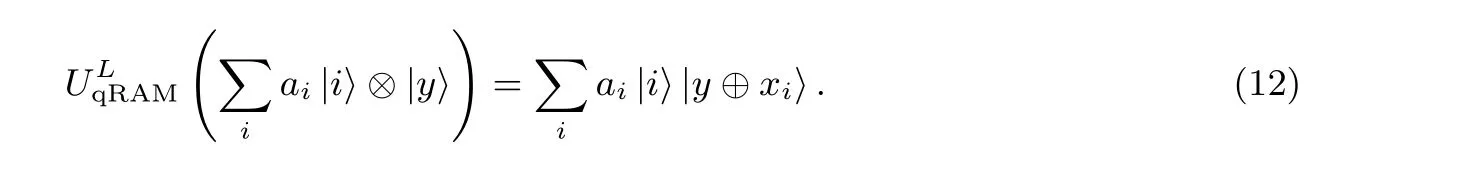
量子存储是否存在, 取决于是否存在一个量子门线路能够实现公式(11)的酉变换.在该表L的量子存储存在的前提假设下, BHT 算法寻找一个随机函数f:{0,1}n {0,1}n的碰撞一共包括两步:

(1) 任意选子集合X ⊂{0,1}n, 集合大小为|X| = 2n/3.对所有x ∈X, 计算f(x), 并将2n/3个对L={(x,f(x))}x∈X存储到量子存储qRAM 中.这一步所需时间是O(2n/3).所需的量子存储大小是O(2n/3).

总之, 在假设存在大规模量子存储qRAM 的前提假设下, 不考虑并行计算, BHT 算法能够以O(2n/3) 的时间复杂度和O(2n/3) 的量子存储找到一个碰撞.

4.1.2 仅需要大规模经典存储的量子碰撞攻击算法

BHT 算法构造碰撞攻击尽管其仅需要时间复杂度O(2n/3),但它们需要O(2n/3)规模的量子存储.目前研究人员普遍认为制造大规模量子存储的难度是巨大的[9,10].因此在没有大规模量子存储的前提下, 是否存在优于生日攻击(复杂度为O(2n/2)) 的量子碰撞攻击算法成为一个公开问题.在2017 年亚密会上,法国密码学家Chailloux 等人首次提出了不需要大规模量子存储的量子碰撞攻击算法[61], 其时间复杂度是O(22n/5), 同时需要O(2n/5) 的经典存储以及O(n) 的量子存储, 我们记该量子算法为CNS 量子碰撞攻击算法.首先, Chailloux 等人给出了一个如何检测某元素是否存在于列表L={x1,x2,···,x2k}, 该列表存储于经典内存中, 大小为2k.

定义1 给定列表L={x1,x2,···,x2k}, 定义一个经典的成员检测函数fL:fL(x) = 1 当且仅当x ∈L, 否则fL(x)=0.

设该经典的成员检测函数fL的量子实现(即量子成员检测函数) 为OL:

当L被存储在经典内存中, Chailloux 等人能够以n2k的时间复杂度和2n+1 量子比特实现OL.CNS量子碰撞攻击算法可以被划分为两部分, 即预计算阶段和匹配阶段.

当设r=2k=2n/5, 公式(15)达到最小值, 即时间复杂度最优, 为O(22n/5).所需的量子比特规模O(n),同时需要规模为2n/5经典存储来存L.

4.2 专用量子碰撞攻击

在量子计算环境中寻找哈希函数的碰撞是很重要的研究方向.最近, 包括美国NIST 后量子公钥密码标准化竞赛候选算法在内的一些公钥密码方案在量子随机预言模型(quantum random oracle model,QROM) 下被证明是安全的[2,62].量子随机预言模型允许敌手以量子叠加态查询公钥系统中的哈希函数,因此其哈希函数不应存在任何比通用量子攻击更有效的专用量子攻击, 包括专用量子碰撞攻击.

在经典计算模型下, 对n比特输出的理想哈希函数的最优通用碰撞攻击复杂度为O(2n/2).在量子计算模型下, 在不同的假设下共有三种通用碰撞攻击:

• 第一种情况中, 假设攻击者拥有指数量级的量子随机存储(qRAM), 在这种情况下的最优攻击为BHT 算法(见第4.1.1 节), 其时间复杂度为O(2n/3), 但它同时需要O(2n/3) 的qRAM.

• 第二种是在没有指数级qRAM, 但是攻击者拥有大规模经典存储的情况下, 最优攻击为Chailloux等人在2017 年亚密会上提出的方法(即第4.1.2 节的CNS 量子碰撞攻击算法), 时间复杂度为O(22n/5), 而需要O(2n/5) 的经典随机存储和O(n) 的qRAM.

在量子计算模型中的这几个不同假设下的通用碰撞攻击将作为评判专用量子碰撞攻击优劣的基准.2020 年欧密会上日本学者Hosoyamada 等人[65]在国际上首次给出了哈希函数的专用量子碰撞攻击, 其在第一种和第三种情况下针对哈希模式AES-MMO 和标准哈希函数Whirlpool 给出了优于通用攻击的量子专用碰撞攻击.他们将经典计算模型下Mendel 等人提出的反弹攻击技术[66]转化为量子的反弹攻击技术.该工作的意义在于指出了那些在经典计算模型下概率低于生日界从而无法使用的差分路线, 在量子计算模型下仍能利用攻击.在拥有大规模量子随机存储易制备的前提下(第一种情况), Hosoyamada 等人[65]针对AES-MMO 和AES-MP 给出了优于BHT 算法的7 轮量子碰撞攻击.在第三种情况下, 他们给出了优于通用攻击的7 轮AES-MMO/-MP 和6 轮Whirlpool 等哈希算法的量子碰撞攻击, 较经典攻击均提升了1 轮.但是, 在第二种情况下, 即攻击者没有大量qRAM, 但是具备大规模经典存储时,Hosoyamada 和Sasaki 未获得攻击复杂度优于CNS 量子碰撞攻击的专用攻击方法.

目前情况下, 无论是制备大规模量子比特或者qRAM 都是非常困难的, 能否制造出大的qRAM 即使在量子计算学界也是一个颇有争议的问题[10,67].因此, 如何在只使用小规模量子计算机, 且使用少量qRAM 或不使用qRAM 的情况下超越Chailloux 等人提出的方法, 便成为一个重要的且较为实际的问题.在2020 年亚密会上, Dong 等人提出了利用非饱和超级S 盒降低qRAM 使用的反弹攻击方法, 并结合量子计算, 提出了一个低qRAM 复杂的量子碰撞攻击方法[68].该工作还指出, 利用Bonnetain 等人给出的一个专用的量子电路在线计算满足一定S 盒输入输出差分的数据对[60], 可以完全避免qRAM 的使用.该工作的意义在于, 其首次给出了在不使用qRAM 的情况下, 超越Chailloux 等人方法的专用量子碰撞攻击.同时, 该工作还给出了一个基于混合整数规划(MILP) 技术, 自动化搜索用于量子碰撞攻击最优差分路线的方法.

在2021 年亚密会上,Dong 等人利用相关密钥差分路线构造基于反弹技术的经典和量子碰撞攻击[69],并构造了基于混合整数线性规划的自动化搜索模型, 搜索适用于构造经典和量子碰撞攻击的差分特征.该攻击的想法是利用密钥自由度, 提高差分路线的概率.在自动化模型建立过程中, 有效地解决了某些哈希函数存在相关密钥差分路线多轮不兼容的情形, 自动化地搜索出有效的攻击路线.基于上述想法, 他们首次给出ISO 标准哈希函数Whirlpool 的9 轮自由起始量子碰撞攻击(free-start quantum collision).

在军事题材的影视作品中，常常出现指战员们站在一个巨大的沙盘前讨论战争形势的情形。传统意义上的沙盘作为地图的补充，弥补了传统军事地图无法形象表现出战场地势地形的缺陷，为广大指战员提供了在和平时期进行战争推演的平台。而全息数字沙盘，在具备传统沙盘的功能的同时，还摒弃了传统沙盘搭建时间长、精度差、重复使用率低的缺陷。并且模块化的硬件使得沙盘可以多次使用，数字影像又实现了在使用时，可以全方位多角度地观察战场。并且其易于储存方便携带的特点，也使得随行保障更加便捷。

在2021 年美密会上, Hosoyamada 等人首次研究了针对SHA-256 和SHA-512 的专用量子碰撞攻击[70], 攻击分别达到38 步和39 步, 显著改进了31 步和27 步的经典碰撞攻击.攻击采用的框架是将许多半自由起始碰撞(semi-free-start quantum collision) 攻击转换为两消息块碰撞攻击.在第三种情况(时空权衡) 下, 能够比并行rho 算法更加高效.Hosoyamada 等人观察到在量子计算条件下, 利用Grover 算法可以显著减少所需的半自由启动碰撞次数, 这使其能够将之前经典的38 步和39 步半自由起始碰撞攻击转换为量子碰撞攻击.该攻击背后的想法很简单, 也将适用于其他密码哈希函数的量子碰撞攻击.

在2022 年美密会上, Dong 等人进一步利用哈希函数消息自由度延长反弹攻击路线[71].一般情况下,反弹攻击包括一个Inbound 阶段和两个Outbound 阶段.如何拉长反弹攻击的轮数是一个重要的密码分析难题.相关研究包括Gilbert 和Peyrin 在FSE 2010 上提出的超级S 盒技术[72], 以及Sasaki 等人在2010 年亚密会上提出的非满活跃盒的超级S 盒技术[73].然而这些技术仅能将Inbound 阶段扩展至2 轮.在上述工作基础上, 文献[71] 提出了名为对角化反弹攻击(triangulating rebound attack) 的新型方法.该方法利用压缩函数中的消息自由度链接多轮Inbound 阶段, 显著延长了反弹攻击的轮数.链接过程需要建立并求解一组关于消息的非线性方程组, 作者利用类似高斯消元(triangulation algorithm, 对角化) 方法[74], 通过合理消耗消息自由度, 高效地求解非线性方程组, 从而成功构造多Inbound 阶段的反弹攻击.该攻击仅需要少量的内存, 这使得其也能够用于构造低量子随机存储的量子碰撞攻击.同时, 作者还提出了基于可满足性问题(constrained programming)建立自动化搜索模型,高效地搜索多轮Inbound 的反弹攻击路线.基于该方法, 作者首次将AES-MMO 的碰撞攻击突破至8 轮.另外, 还给出了Saturnin-Hash、Grøstl-512、SKINNY-128-384-MMO/MP 等哈希函数的多个减轮的经典和量子碰撞攻击.

除了上述分析外, Flórez-Gutiérrez 等人[75]给出了Gimli-Hash 的自由起始量子碰撞攻击.Kumar等人研究了基于Hirose 双分组哈希模型下的AES-256 (记为HCF-AES-256, 全轮14 轮) 的量子碰撞攻击[76].Ni 等人研究了Simpira v2 置换函数在Davies-Meyer 哈希模式下的量子碰撞攻击[77].Guo 等人给出了SHA-3 哈希函数减轮的量子碰撞攻击[78].这些攻击意味着在量子计算模型下, 可以用于攻击的密码特征范围被大大扩展了.因此, 如何搜索这些特征并利用它们进行基于量子计算的密码分析会成为对称密码分析和设计领域的一个重要问题.

4.3 哈希函数的量子原象攻击

给定一个n比特摘要, 利用Grover 算法可以在2n/2的时间复杂度下搜索出原象.在专用量子原象攻击方面, Schrottenloher 和Stevens 在2022 年美密会上提出了量子中间相遇攻击(quantum Meet-inthe-Middle, quantum MitM) 求解原象[79].该算法的核心是找到两个列表中相等的元素, 被称为双列表融合量子算法(quantum two-list merging algorithm).假设在中间相遇过程中, 需要遍历一个全局猜测空间Fg2, 对于每一个猜测G ∈Fg2, 攻击者可以构造两个列表L1和L2, 并判断是否存在x ∈L1和y ∈L2,使得x=y.令Omerge是如下的酉变换:

Schrottenloher 和Stevens 给出量子中间相遇的如下引理:

引理1[79](量子中间相遇攻击) 实现Omerge的时间复杂度是

其中Lmerge是一个融合后的列表.实现Omerge所需的量子随机存储大小为min(|L1|,|L2|).因此, 量子中间相遇攻击的复杂度为:

此外, Wang 等人[80]结合旋转攻击给出了Keccak-224 的4 轮量子原像攻击.Chen 等人[81]提出了一个求解布尔方程的量子算法, 并应用到了哈希函数的原像攻击中.

4.4 哈希函数的多目标原象攻击(Multi-target preimage attack)

定义 2 (多目标原象攻击) 给定一个随机函数H:{0,1}n {0,1}n以及一个摘要集合T={y1,y2,···,y2t}, 找到一个集合T中某一个元素yi的原象, 即找到i ∈{1,2,···,l}和x ∈{0,1}n,满足H(x)=yi.

在经典计算模型中, 上述多目标原象攻击的复杂度约为O(2n−t).在SAC 2017 上, Banegas 和Bernstein 介绍了并行的量子多目标原象攻击[82].假设量子随机存储跟经典随机存储一样能够简单制备,那么将T存储于量子随机存储中, 可以利用Grover 算法搜索x, 使得H(x) 在T中.这种情况下, 量子多目标原象攻击的时间复杂度约为O(2(n−t)/2), 所需量子随机存储的大小是2t.

在CNS 量子碰撞攻击的论文中, 作者亦给出了在量子随机存储非常昂贵的情况下, 用经典随机存储构造量子多目标原象攻击的方法[61].其所需的时间复杂度是2n/2−t/6+min{2t,23n/7}, 所需的量子随机存储为O(n), 所需的经典随机存储是min{2t/3,2n/7}.当t= 23n/7时, 整体复杂度达到最优, 即时间是23n/7, 经典随机存储是2n/7.

4.5 多碰撞问题(Multi-collisions)

4.6 广义生日攻击的量子解法

广义生日攻击问题的经典模型最优解法是Wagner 提出的[87], 其所需经典时间复杂度和存储均为O(2n/(t+1)), 其中k=2t.在2018 年亚密会上, Grassi 等人[88]在攻击者具有多项式规模量子存储、指数规模量子存储两种假设下给出了多种广义生日攻击的量子解法.在2020 年欧密会上, Naya-Plasencia 等人在不需要量子存储的假设下, 给出了广义生日攻击的最优量子算法[89], 同时给出了在不需要查询量子预言机的假设下的量子求解算法.在SAC 2021 上, Schrottenloher 针对仅具有唯一解的广义生日攻击问题, 提出了一般性量子算法[90].

4.7 预言者攻击(Nostradamus attack)

在2022 年亚密会和NSS 上, Benedikt 等人[94]和Bao 等人[95]分别独立研究了量子计算模型下的预言者攻击, 其所需的量子时间复杂度是O(20.43n) 且需要O(20.43n) 规模的量子存储.在亚密会文章中作者还提出了如何在不使用量子存储的情况下设计量子攻击算法的公开问题.随后, 在ToSC 2023 上,Zhang 等人利用中间相遇攻击给出了AES 类哈希函数的专用量子和经典的预言者攻击[96].在2023 年亚密会上, Dong 等人[97]解决了2022 年亚密会上Benedikt 等人提出的公开问题, 提出了不使用量子存储的新型量子预言者攻击, 其攻击的时间复杂度相较于Benedikt 等人的攻击仅由O(20.43n) 略微上升至O(20.46n).该文章还提出了其他一些哈希结构(如, 哈希异或组合H1⊕H2、哈希级联组合H12、两次哈希、Zipper 哈希等) 的量子原像、量子碰撞、量子预言者攻击等.在ToSC 2024 上, Dong 等人[98]利用其提出的不使用量子存储的量子预言者攻击, 结合中间相遇攻击方法, 改进了AES 类哈希函数的专用量子和经典的预言者攻击.

5 总结和展望

对称密码的量子分析研究是自2010 年之后才开始蓬勃发展的研究方向, 十余年来所取得的重要进展表明量子计算模型能够显著提升对称密码的攻击效果, 甚至在某些量子攻击假设下, 某些经典密码算法可以被量子多项式时间破解.另一方面, 在密码分析过程中, 研究者设计了新的量子算法, 这些算法反过来又促进了量子计算的进步.在后续研究中, 以下几个研究方面值得进一步探索:

量子算法设计与创新: 针对RSA 公钥密码的大整数分解问题, Peter Shor 设计了Shor 算法.因此,针对密码基于的数学问题设计高效的量子求解算法是密码分析的重要研究方向.同时, 挖掘和应用已知的量子算法进行密码分析也是重要研究内容.目前密码学者已将多种量子算法应用于密码分析, 包括Grover算法、Simon 算法、Kuperberg 算法等.甚至, 密码学者可以将多种量子算法加以结合, 设计出针对具体密码算法的新型量子分析方法, 如Grover 和Simon 的结合使用、Grover 和Kuperberg 的结合使用等.

经典计算模型下的密码分析技术的量子化: 对称密码的经典分析方法已经发展了四十余年, 期间积累了众多经典分析方法,包括中间相遇攻击、差分分析、线性分析、不可能差分分析、零相关密码分析、代数攻击、反弹攻击等.如何利用量子算法将这些经典分析方法量子化,并提升分析效果,是一个重要的研究方向.