认知智能电网中基于非合作博弈的电视频谱资源共享研究

刘明轩，杨 亮，赵 越

（福州大学 电气工程与自动化学院，福建 福州 350108）

0 引言

随着通信控制技术的发展，传统电网逐渐向智能化转变。智能电网信息流交互系统从逻辑上分为3层：家域网（Home Area Networks，HAN）、邻域网（Neighborhood Area Networks，NAN）和广域网（Wide Area Networks，WAN）。认知无线电（Cognitive Radio，CR）主要应用在NAN中。文献[1]提出一个通信网络架构，可以利用电视空白（TV White Space，TVWS）频谱，以支持智能电网应用在大规模的住宅、商业和工业设施，同时根据智能电网的应用需求提供服务质量（Quality of Service，QoS）保证。在CRNAN中，每个次用户如何最大限度利用TVWS频谱是需要解决的关键问题。文献[2]研究探讨将TVWS频谱应用在NAN中，基于公平性和优先级，使用布谷鸟搜索算法提出一种联合功率和信道分配方案。文献[3]提出一种NAN场景下的动态频谱分配方法，以保证在QoS要求的约束下，频谱资源能够得到充分的分配和利用。在频谱资源的分配中，功率控制尤为重要。文献[4]提出一种基于势博弈的联合频谱和功率分配算法，该算法能够快速收敛到稳定的纳什均衡，提高了网络的整体效率。文献[5]提出一种主成分分析（Principal Component Analysis，PCA）算法来解决CR网络的功率控制问题。所提出的解决方案模型是无线系统与非合作的博弈，其中每个博弈的参与者在竞争环境中最大化发挥其效用。在CRNAN的网络模型中，文献[6]证明了需求响应管理（Demand Response Management，DRM）性能随通信中断概率提高而降低，并提出一个联合空间和时间频谱共享方案，建立一个广播模型，按照不同距离对频谱共享的模式划分成功率控制区域和自由区域，但是并没有具体研究功率控制的方法。在现有成果的基础上，建立认知智能电网中邻域网的TVWS频谱共享模型，并使用非合作博弈算法研究网络模型中的功率控制问题。

1 系统模型

CRNAN频谱共享模型如图1所示。在图1中，考虑具有位于半径R的圆形区域中的多个主用户（Primary Users，PU）和次用户（Secondary Users，SU）的网络模型。其中，PU是电视频谱的拥有者，SU是SG节点，是配备有智能仪表以将数据传输到无线接入点（Access Point，AP）的电量消费者。无线AP的任务是从每个SG节点收集电力需求信息，并从控制中心向所有连接的SG节点广播价格信息。SU与PU动态共享可用的许可频谱。主发射机（Primary Transmitter，PT）位于模型的中心，围绕主发射机的是半径为R1的独占区域，PU均匀分布在主发射机周围的独占区域内，分布密度为μ。对于SU来说，虽然无法得到PU的确切位置，但是可以检测主发射机的位置，因此SU为了满足干扰约束，便不能在独占区域内工作，避免PU处的聚合干扰达到无限大。

图1 CRNAN频谱共享模型

假设所有SU均匀分布在独占区域外，分布密度为μ，所有SU的最大发射功率为Ps。考虑无线信道的路径损耗模型，给定发射机与接收机之间的距离d，则信道增益为

式中：A为频率相关常数，α为功率路径损耗。为了便于计算，将A归一化为1，考虑α＞2。

R1是PU的频谱独占区域，在这个区域内SU不能共享频谱，以避免对PU造成干扰。R1到R2的区域称为内层区域，在该阈值距离R2内，SU只能在PU未使用频谱的情况下共享频谱。R2到R3的区域称为功率控制频谱共享区域，在这个区域内的SU可以和PU同时共享频谱，但是必须采用功率控制的方式。超过R3的区域由于距离PU过远，对其产生的干扰可以忽略，SU可以采用最大发射功率，因此R3以外为自由频谱共享区域。根据文献[6]可知，各区域的表达式为

式中：P0为PT的发射功率，σ2为噪声功率谱密度，C0为常数。

式中：Ps为最大发射功率，Ath为常数。

式中：Ith为干扰功率的阈值，β(β<1)为常数。

由此可得频谱共享区域的中断概率为

式中：D0=为次用户到AP节点之间的路径损耗，Pi为发射功率，R为整个网络的半径，Cs为数据传输的阈值速率，Pr(·)为SU的传输速率小于阈值速率的概率，即SU通信中断的概率。

2 功率控制博弈

为了解决SGNAN频谱共享过程的干扰问题，提出一个功率控制模型。考虑R2～R3的每个客户端单元（Client Unit，CU）在PU拥有的相同频带上通过发射功率Pi进行通信，基站和用户都是单天线的情况下，第i个CU的信干噪比（Signal to Interference and Noise Ratio，SINR）为

式中：hi为第i个SU到AP节点之间的路径增益，hj为除了第i个SU外其他SU与AP节点之间的路径增益，Pj为除了第i个SU外其他SU的发射功率。

为了满足认知用户自身的QoS，每个CU的接收信号与SINR应满足γi≥γi,th，其中γi,th为SU维持QoS所需的SINR。当SU的SINR值较小时，节点可以通过适当增加发射功率的方式来改善SINR，前提是不能影响PU的正常通信。为了确保PU的通信不受CU传输的影响，来自CU的最大干扰必须小于由PU定义的干扰阈值Ith，PU总接收干扰功率应满足

2.1 博弈模型

在认知无线网络中，SU会选择最佳功率实现效用函数最大化，而非合作博弈关注的正是个体的决策最优化，因此SU的功率控制适合采用非合作博弈模型来处理。非合作功率控制模型可以表示为

式中：N={1,2,…,3,N}为所有SU的集合，pi为SU策略空间的集合，即发射功率集合，p-i为不包括pi在内的策略集合，ui(pi,p-i)为每个SU的效用函数。在功率控制博弈中，每个SU都设法提高自身的效用函数，即 maxui(pi,p-i),∀i∈N。

2.2 效用函数

在所提出的博弈模型中，每个参与者的效用即既取决于自身的策略，又取决于其他参与者的策略，因此对第i个参与者，可以采用效用函数。

式中：pi∈[0,pi,max]，Ai为SINR影响因子，Bi、Ci为功率影响因子。

效用函数代表博弈中每个SU所获得的收益大小，该函数由收益函数和代价函数两部分构成。收益函数表示博弈参与者对网络及系统服务质量的满意水平，而代价函数则表示博弈参与者在获得利益的同时必须消耗的能量。当系统中用户数量较少时，此时系统干扰较小，为了充分利用资源，用户可以通过适当增加Ai的值达到提高SINR的目的。Bi和Ci为功率影响因子，当某些SU的发射功率过大，甚至超过功率阈值太多时，这些用户将受到较大的惩罚。

2.3 功率控制算法

提出一个自适应功率控制算法，保证SU的发射功率达到最优水平，使博弈收敛到纳什均衡点。纳什均衡（Nash equilibrium，NE）被定义为博弈中的一个点，在博弈中每个参与者都能获得最佳收益，并且没有一个参与者可以通过偏离自身的策略单独提高收益。

当且仅当ui(pi*,p-i)≥ui(pi,p-i),∀pi∈si时，功率向量S=p1,p2,…,pi,…,pN是博弈G∀i∈N的纳什均衡，其中pi表示第i个SU的发射功率，pi*表示NE处第i个SU的发射功率，p-i表示除第i个SU外其他用户的发射功率。

对效用函数ui(pi,p-i)求一阶导可得

这表明第i个SU受到的干扰由除第i个SU外其他所有SU引起的干扰和高斯白噪声引起。

将式（7）带入式（13）求解pi，得到第i个SU的最优发射功率为

运用牛顿迭代法得到SU发射功率的迭代公式为

每个CU使用式（15）来调整自身的发射功率，直到算法收敛到最佳发射功率。基于非合作博弈的功率控制算法的具体过程如下。

输入：PT发射功率，SINR阈值，SU最大发射功率，迭代误差值

输出：pi和γi的迭代值

步骤1：设置SGNAN中SU的数量N

步骤2：For i=1∶Ndo

步骤3：设置SU初始发射功率pi(0)

步骤4： 通过式（7）计算γi(0)

步骤5： 通过式（9）计算ui(0)

步骤6：End for

步骤7：Fori=1∶Ndo

步骤8：Sett=1

步骤9：Repeat

步骤10：Ifγi<γi,th，then

步骤11：通过式（15）更新pi(m)

步骤12：通过式（13）更新γi(m)

步骤13：通过等式（9）更新ui(m)

步骤14：end if

步骤15：t=t+1

步骤16： Until |ui(m+1)-ui(m)|<ε

步骤17：end for

2.4 NE存在性和唯一性的证明

NE存在性的效用函数必须满足以下两点：第一，效用函数的凸集必须非空、有界，即参与者的个数是可数的有限个数；第二，证明效用函数是一个连续的拟凹函数。拟凹函数是指以横坐标轴作为基准，图像的曲线都是上凹形状的函数，对定义域内任意x，y，有

一方面，对于每个次用户i的策略空间都定义在区间[pi,min,pi,max]，其个数默认是有限的，因此效用函数满足NE存在的第一个条件。另一方面，从拟凹函数的定义可知，可以采用效用函数二次求偏导的方法来证明凹凸性，若效用函数的二次导数小于0，则其为拟凹函数，反之就是凸函数。为了证明所提出的效用函数为拟凹函数，将效用函数对pi求导两次得出

γi>γi,th，Ai、Bi和Ci为恒定且非负，因此有由此可知ui(pi*,p-i)是一个连续的拟凹函数，该效用函数具有NE解。

非合作博弈算法pi,k+1=fi,k(pi,k)收敛且具有唯一NE解，必须满足以下3个条件。第一，函数的恒正性：f(pi)>0。第二，函数的单调性：如果pi>pi′，则有f(pi)>f(pi′)。第三，函数的扩展性：αf(pi)-f(αfi)>0，∀α>1。下面将根据以上条件对NE的相关性质进行证明。

首先，因为Ai和Bi都大于0，所以f(pi)>0，条件1成立。

其次，由于pi>pi′>0，则

可知条件2成立。

最后，利用式（20）分析其扩展性，即

因为α>1，所以，αf(pi)-f(αfi)>0，所以条件3成立。

由此可见，文章提出的非合作博弈算法pi,k+1=fi,k(pi,k)收敛且具有唯一NE解。

3 仿真结果与分析

对所提出的方案进行性能评估，通过MATLAB仿真实现。假设PT位于网络的中心位置，发射功率P0=10 W，PU均匀分布在PT到R1的圆形范围内，在R2到R3内随机分布。SU的最大发射功率Pmax=1 W，初始发射功率pi(0)=5×10-15W，SINR的阈值γi,th=7 dB，A=1，ε=10-15，α=4，σ2=10-6，μ=0.01，Ath=11 309.73，C0=0.1，Cs=0.1，β=0.02，Ai=1，Bi=0.5，Ci=1。根据以上参数的设置，计算得到频谱共享模型的范围，其中PU独占区域为半径R1=108 m，R2=146 m，R3=809 m，因此频谱共享模型中采用功率控制的SU主要分布于半径146～809 m的环形区域内。

采用非合作功率控制算法的情况下，SU发射功率和迭代次数之间的关系如图2所示。从图2可以看出，在主发射机PT发射功率P0保持恒定的情况下，每个SU的发射功率取决于其与AP节点之间的距离，距离较远的SU会增加发射功率以达到门限SINR值，而位于AP节点位置较近的SU则以较低的发射功率进行通信以节省能量。

图2 SU的发射功率迭代情况

文章提出的功率控制算法和文献[5]中PCA算法的SU平均发射功率的迭代情况如图3所示。由图3可知，PCA算法收敛速度较快，在迭代30次后收敛，所提出的功率控制算法在迭代50次左右时发射功率达到收敛状态，但是所提算法中SU的平均发射功率比PCA算法大约降低7%，有效降低了能耗。

图3 不同算法SU的发射功率

不同距离的SU的SINR收敛值情况如图4所示。SU随着距离的增加，功率控制算法会动态调整参数以提高其发射功率，保证SINR在阈值以上。SU的信噪比一直高于最低服务质量所对应的最低信噪比值，说明算法能够以较低的发射功率取得SU对服务质量的需求，有效降低对周围用户的影响，减轻对认知网络和PU的干扰和噪声，很好地实现了功率控制目标，提高了频谱利用率和认知网络的能效性。

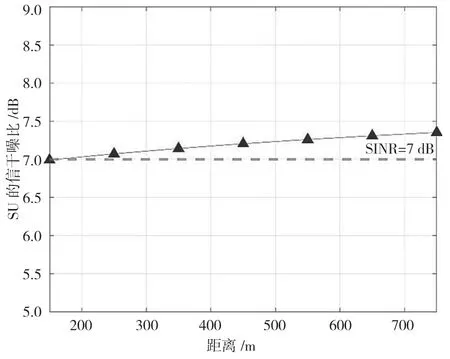
图4 距离PT不同位置SU收敛后信干噪比

距离PT不同位置SU中断概率如图5所示。当主发射机PT的发射功率P0固定时，SU的中断概率随着距离的增加而增加，距离较近的SU大部分中断概率低于0.1。小部分距离较远的SU即使其中断概率处于0.1～0.2，整个系统的平均中断概率小于0.07，说明所提出的功率控制算法能够提供良好的DRM性能。

图5 距离PT不同位置SU中断概率

4 结语

文章研究了认知智能电网中的TVWS频谱共享问题，建立一个Underlay方式下的频谱共享模型，并在共享模型上提出一个非合作功率控制博弈来解决频谱共享过程的功率分配问题。一方面在满足QoS的情况下降低SU的发射功率并保护PU免受有害干扰，另一方面提高了网络中频谱的利用率。博弈的结果通过实现NE进行分析，并从数学上证明了NE的存在性和唯一性。最后给出仿真结果，证明所提算法的有效性。在未来的工作中，对于无法在Underlay模式下进行频谱共享的SG节点可以采用Overlay模式进行频谱共享的研究。