Deep Reinforcement Learning-Based Task Offloading and Service Migrating Policies in Service Caching-Assisted Mobile Edge Computing

Ke Hongchang ,Wang Hui ,Sun Hongbin ,Halvin Yang

1 School of Computer Technology and Engineering,Changchun Institute of Technology,Changchun 130012,China

2 College of Computer Science and Engineering,Changchun University of Technology,Changchun 130012,China

3 Department of Electronic and Electrical Engineering,University College London,London,UK

Abstract: Emerging mobile edge computing(MEC)is considered a feasible solution for offloading the computation-intensive request tasks generated from mobile wireless equipment(MWE)with limited computational resources and energy.Due to the homogeneity of request tasks from one MWE during a longterm time period,it is vital to predeploy the particular service cachings required by the request tasks at the MEC server.In this paper,we model a service caching-assisted MEC framework that takes into account the constraint on the number of service cachings hosted by each edge server and the migration of request tasks from the current edge server to another edge server with service caching required by tasks.Furthermore,we propose a multiagent deep reinforcement learning-based computation offloading and task migrating decision-making scheme(MBOMS)to minimize the long-term average weighted cost.The proposed MBOMS can learn the near-optimal offloading and migrating decision-making policy by centralized training and decentralized execution.Systematic and comprehensive simulation results reveal that our proposed MBOMS can converge well after training and outperforms the other fvie baseline algorithms.

Keywords: deep reinforcement learning;mobile edge computing;service caching;service migrating

I.INTRODUCTION

In heterogeneous wireless networks,mobile wireless equipment (MWE) generates a quantity of computation-intensive tasks(such as unmanned vehicle maps,somatosensory games,virtual reality/augmented reality(VR/AR)),which cannot be processed locally by their own processor due to limited resources[1,2].Therefore,how to process and complete these request tasks within a stringent latency constraint for management of heterogeneous networks is a critical issue,such as ameliorating the quality of service(QoS),minimizing the total cost or maximizing the overall utility[3].

Emerging mobile edge computing (MEC) technology is a promising paradigm for transmitting the request tasks of MWEs to edge servers by uplink wireless channels.In addition,the rich computational resources of the MEC server can meet the computational demands of request tasks from MWEs [4,5].The proximity of the MEC server to MWEs makes the transmission tasks extremely convenient and backhaul latency low[6,7].The request tasks can be easily offloaded to the MEC server with powerful computation ability,which can not only improve QoS but also strengthen MWE’s adaptability for computationintensive or latency-sensitive applications [8].There have been many works on computational offloading or resource allocation in the MEC environment.Liuet al.formulated a method for job scheduling of MEC resources in multiuser scenes.The method could utilize the improved heuristic algorithm (binary-relaxed solution) to make the job placement decision to minimize the long-term slack time of users[9].Shenget al.presents a computation offloading decision-making policy in the MEC scenario to minimize the average latency cost of all users.The mentioned scheme considered power allocation,resource allocation and computational offloading based on optimization theory and matching theory[10].However,in[9,10],the works assume that the computational resources of the MEC server are suffciient for multiuser scenes.In fact,although the resources of MEC servers are abundant,the computation-intensive tasks of massive users will overwhelm MEC servers.

Because of the homogeneity of request tasks from one MWE during a long-term time period,it is vital to predeploy the particular cachings required by the request tasks at the MEC server.Caching can be typed as content caching and service caching.Content caching is the static content (such as video and gaming)in the content buffer of the MEC server[11,12].However,service caching can be viewed as caching of dynamic content.The dynamic content here is the executable program,which is called computation realized by the program such as required libraries,databases,or computation resources for executing the request tasks.In terms of content caching in the MEC environment,the static characteristic of that is considered,such as Sunet al.proposed a joint optimization scheme for caching and computing VR in an MEC system [13],HUYNHet al.implemented an edge caching MEC network to fnid the optimal decisionmaking policy.There are a bit existing works on service caching.Liet al.introduced a computational offloading decision-making policy in a service cachingassisted MEC network using game theory to obtain the minimum power consumption cost under the time constraint[14].Chenet al.formulated a service cachingassisted offloading optimization scheme to minimize the long-term average task fniished delay[15].However,the aforementioned works in[14,15]did not consider the time-varying channel state between mobile users and MEC servers or cloud servers and resource sharing among MEC servers.In addition,game theory and the ADMM optimization method consider individuals more than resource competition.

Since the introduction of deep reinforcement learning (DRL),signifciant results have been achieved in both theory and application in artifciial intelligence[16].There are several DRL algorithms composed of value-based methods(deep Q-Learning(DQN)[17],double DQN (DDQN)[18],and dueling DQN[19]),policy-based methods(policy gradient(PG)[20],proximal policy optimization (PPO)[21]),and combining policy and value methods (actor-critic) [22] and deep deterministic policy gradient(DDPG)[23]).There are many works on DRL-based computation offloading or task migrating in MEC frameworks,such as Liuet al.designed a multiuser system and proposed a DQNbased offloading optimization policy[24],Elgendyet al.utilized the Q-Learning and DQN algorithms to tackle the joint offloading and caching optimization problem [25].Wanget al.presented a joint computation migration and resource allocation policy based on DDQN in vehicular networks[26].However,in[24-26],the mentioned DRL-based schemes are single agent or arbitrary decentralized multiagent learning patterns that are not suited for the massive MWE and MEC server scenarios in heterogeneous MEC networks.

Deep multiagent reinforcement learning (MARL)algorithms can train neural networks in centralized or decentralized patterns,which have been applied in MEC environments in some existing works.In terms of state-of-the-art MARL-based scheme,Gonget al.designed a joint optimization scheme based on the multiagent deep deterministic policy gradient(MADDPG)for fniding near-optimal offloading,computational resources and power allocation decisionmaking policy to minimize the total overhead composed of delay cost and energy consumption cost[27].Seidet al.formulated the joint optimization for offloading,computation allocation and association problem to stochastic game (SG) and used the MADDPG algorithm with centralized training and decentralized execution characteristic to learn the nearoptimal decision-making policy for obtaining the minimum computation cost of total MEC system[28].Although the aforementioned works in [27,28] implemented the MARL-based solution for computationintensive tasks from multiple users in a multi-edge server environment,they did not take into account the interaction among different MEC servers and the timevarying achievable capacity of MEC servers.However,there were also some state-of-the-art schemes related to our work.Houet al.transited the offloading optimal problem into Partially Observable Markov Decision Process(POMDP)and constructed the deep neural network based on Double Deep Q Network(DDQN)to learn the optimal offloading decision[29].The designed MEC environment of[29]was more theoretical,without considering the randomness of request tasks generated by MWEs and the time-varying characteristic of channel state.Sunet al.formulated a multi-user and multi-cell MEC framework and proposed a multi-branch network DDQN-based computation offloading and resource allocation decisionmaking policy to obtain the minimum task delay and discard rate [30].Although the work in [30] implemented offloading decisions for multi user terminals in a multi edge server environment,it did not considered cooperative scheduling between edge servers.Once the resource of an edge server was insuffciient or did not have the required service caching for specifci tasks,it will affect effciiency of algorithm.

To address aforementioned challenges,in this paper,we design a multi-service caching-enabled MEC network and propose an MADDPG-based computation offloading and task migrating decision-making scheme(MBOMS)to fnid the optimal policy for minimizing the long-term average weighted cost,including the latency cost and energy consumption cost.To the best of our knowledge,our work is the frist to jointly consider the randomness of the request tasks generated by the MWE,the time-varying channel between the MWE and the edge server,the changing capacity and hosted service caching of the edge server,and the different priorities of request tasks.

The main contributions of our work are illustrated as follows:

• To effectively tackle the computation-intensive request tasks generated by the resource-limited MWEs,we design a service caching-assisted MEC framework that takes into account the constraint on the number of service cachings hosted by each edge server and the migration of request tasks from the current edge server to another edge server with service caching required by tasks.

• By considering a multiuser MEC network model with a time-varying channel state,the changing capacity of the edge server,and the different priorities of request tasks,we formulate the joint offloading and migrating problem as an MDP to minimize the long-term average weighted cost,including the latency cost and energy consumption cost.

• Because of noprioriknowledge of state space and state transition probabilities in each time slot,we transit the MDP-based scheme to the MADDPGbased problem.Each MWE can act as a learning agent and interact with the MEC environment.By offline training of the neural networks of the MADDPG model,the near-optimal offloading and migrating policy can be learned with centralized training and decentralized execution.

• To evaluate and verify the convergence and effectiveness of the proposed MBOMS,we perform systematic and comprehensive numerical simulations.Different parameter confgiurations for MBOMS in the simulation results reveal good convergence,and a comparison with fvie baseline algorithms indicates the robustness and superiority of MBOMS.

The rest of this paper is organized as follows.A service caching-enabled MEC network model is introduced in Section II.Section III illustrates the joint offloading and migrating scheme for minimizing the average weighted cost of the overall MEC system.In Section IV,an MADDPG-based optimization scheme for offloading and migrating decisions is proposed.Section V provides the systematic numerical simulation results.Our work is concluded in Section VI.

II.SYSTEM MODEL

To better describe the system model,in this section,we consider a service caching-assisted MEC system composed of the network model,the communication model,and the computation model.

2.1 Network Model

We designed a three-tier architecture system assisted with service caching,including the mobile user layer,the MEC layer,and the cloud layer.Figure 1 shows the edge server framework assisted by service caching.We denoteE={1,2,···,E},R={1,2,···,R},andC={1,2,···,C}as the set of MWEs,request tasks,and service cachings,respectively.Each request task from MWEs requires certain service caching for computing.We assume thatre,c,re,c ∈Ris a request task generated by MWEe,which needs service cachingc.N={1,2,···,N}stands for the set of edge servers.M={1,2,···,M}andU={1,2,···,U}are the sets of MEC servers and UAVs,respectively.We can see thatN=M ∪U,andM ∩U=∅.Furthermore,we assume that if edge servern(MEC servermor UAVu) hosts the server c achingc,taskre,ccan be executed by edge servern;otherwise,it cannot,whereis the subset ofC.

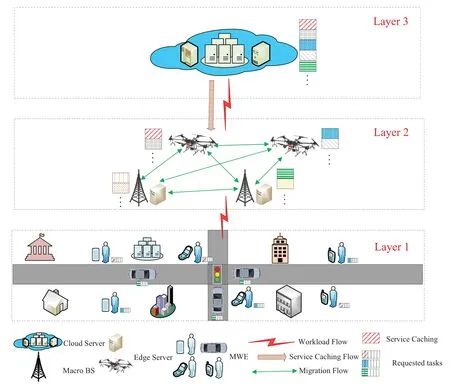
Figure 1.Service caching-assisted MEC framework.

Since each edge server cannot host all cachings,if the edge server does have the service caching required by the request task,these tasks can be migrated to the edge server with the corresponding service caching for processing.If all server edges do not host the server caching required for the request task,the task can be offloaded to the cloud server for processing.To this end,we defnieωr,ωr,nas the migrating decision and migrate to which edge server for taskre,c,meetingωr ∈[0,1],ωr,n ∈[0,1,...,N].That is,if taskre,con edge servernneeds to be migrated to another edge server or offloaded to the cloud server,ωr=1;otherwise,ωr=0.If taskre,con edge servernmigrates to edge serverand if taskre,con edge servernis offloaded to the cloud server,ωr,n=0.Table 1 lists the main parameters and descriptions in our work.

Table 1.List of main notations.

2.2 Communication Model

We consider discretizing the continuous time period to the time slot (certain time intervals),which is defnied asT={1,2,···,T}.The channels between the MWE and the edge server,the edge server and the cloud server are time-varying in different time slots,but they are the same in each time slot.We assume that an MWE can only communicate with the edge server(an MEC server or a UAV) closest to it regardless ofthe remaining computing resources and hosted service cachings of the edge server in each time slot.That is,if the MWE generates the request tasks,the tasks are frist offloaded to the edge server closest.Then,the tasks are migrated to the other edge server or offloaded to the cloud server according to the service cachings hosted by which edge server.We defnie the channel state between MWEEand the edge servernin time slottas

whereρe,npresents the path-loss coeffciient.αe,nis the constant for controlling the scale of the channel state.Schannel(t) is the channel state in current time slot.de,n(t)stands for the distance between MWEEand the edge servern.

In our paper,the channel states are time-varying in different time slots and modeled as a Markov distribution,meetingAn,c=P(Schannel(t+1)=pk|Schannel(t)=pl),whereAn,cis the channel state transition probability matrix,pk,pl ∈Schannel,andSchannelis the channel state vector.

The maximum offloading transmission rate between the MWEeand the edge servernby Shannon’s law can be computed by

whereζnis the ratio of bandwidth allocated to MWEefor offloading the request tasks andWnstands for the total bandwidth of edge servern.pe,n(t) represents the offloading transmission power for tasks from MWEeto edge servern.σn(t)denotes the variance of the additive white Gaussian noise(AWGN)with zero mean.

2.3 Computation Model

As shown in Section 2.1,a certain request task requires particular server caching,which can greatly alleviate the computational pressure on the edge server;for example,the real-time scene map for unmanned vehicles needs the particular server caching located at the edge server or cloud server.To this end,the request task can be offloaded to the edge server with server caching for computation by wireless communication.We defnie the request tasksre,c(t) in time slottas the tuple,meetingwhereis the total size of request tasksre,c(t),stands for the computation density(number of required CPU cycles) for request tasksre,c(t),andrepresents the constraint on completion time(the deadline for completing request tasksre,c(t)).is the priority of completing request taskre,c(t).Furthermore,we defniePr(t)as the arrival probability of request tasksrfrom MWEein time slottfollowing a Bernoulli distribution withνe.Thereafter,the arrival probability meets E[Pr(I(re,c(t)=1))]=νe,whereI(.) is the indicator function,which means that if MWEegenerates the request tasksre,c(t),I(re,c)=1;otherwise,I(re,c)=0.

2.3.1 Computation Offloading to Edge Server

We defnieBn,qas the task buffer queue for storing the different priority request tasks from the linked MWE.Therefore,the transmission latency for offloading the tasks from MWEeto edge serverncan be calculated by

Accordingly,the energy consumption for transmitting the offloading tasks from MWEeto edge serverncan be calculated by

If edge servernhosts service cachingcfor request taskre,coffloaded by NWEe,edge serverncan execute request taskre,cby its own allocation computation resource with service cachingc,and the execution latency of computing request taskre,cis derived by

wherefe,c(t)is the total number of allocated CPU cycles by edge servernfor computing request taskre,c.In this paper,fe,c(t) is related toand can be defnied as

To this end,the executed energy consumption of computing the request taskre,cis[33]

whereκnstands for the achievable switched parameter based on chip architecture characteristics of the edge servern.

Because one edge server needs to process multiple request tasks,we defnie the task buffer queues to relieve the computing pressure of the edge server.Therefore,request tasks are frist stored in the buffer queue,so the total latency of completing tasks includes the waiting latency,which is computed as

whereξn,qis the weighted coeffciient,which is related to the priorityof request tasks,and according to Little’s Law,waiting latency is proportional to the total length of buffer queueBn,q.

The waiting energy consumption can be defnied as

2.3.2 Migration Tasks to the Other Edge Server

Once the edge serverndoes not host the service cachingcrequired by the offloaded request tasksre,cfrom the MWEe,request tasksre,ccannot be executed by the edge servern.Therefore,the request tasks may be migrated to the other edge server if it hosts service cachingc.Under these circumstances,we should consider the migration latency,which can be written as

Accordingly,the energy consumption for task migration from edge servernto edge serveris

2.3.3 Computation Offloading to Cloud Server

If all edge servers do not host the service cachingcrequired by the offloaded request tasksre,cfrom the MWEe,the tasksre,cneed to be offloaded from the edge server to the cloud server for execution.Therefore,the transmission latency for offloading tasks from the edge servernto the cloud server can be written as

To this end,the energy consumption for transmitting the offloading tasks from edge servernto the cloud server is derived by

Compared with edge servers,cloud servers have suffciient computational resources and service cachings,and the execution latency,energy consumption,waiting latency,and energy consumption can be ignored.However,we consider the downlink transmission latency and energy consumption for the computation result from the cloud server to the edge servern,which are defnied as

III.PROBLEM FORMULATION

We can attempt to determine the migration decisionωrand migration policyωr,nto minimize the long-term weighted average cost for completing all request tasks in the proposed MEC framework during the total time periodT.First,we can compute the total latency and the total energy consumption for the request tasksre,cgenerated by the MWEein the time slott,which are derived as

whereI(·)is the indicate function meetingI(·)=1 if the condition is true;otherwise,I(·)=0.

To this end,the weighted average cost composed of the latency cost and the energy consumption cost for each request taskre,cof the MWEein time slottcan be derived by

whereη1,η2are the weight parameters for the latency cost and the energy consumption cost,respectively,meetingη1+η2=1.

Accordingly,the goal of the paper is to seek the optimal migrating and offloading decision-making policy to obtain the minimum long-term weighted average cost for all request tasks of the MWE during the whole periodT.Therefore,minimizing the long-term weighted average cost problem is defnied as follows:

where C1 stands for the migration decision-making limitation condition,which is the binary variable.In terms of C2,request tasks can be offloaded to the cloud server when all edge servers do not host the service caching required by tasks,ωr,n(t) is set as 0.Request tasks can be migrated to the edge server who hosts service caching required by tasks.The range ofωr,n(t)is[1,2,...,N].Accordingly,one edge server regardless of the MEC server or UAV can only host limited server cachings whose number is less than that of the cloud server on limitation C3.C4 indicates that in each time slot,an MWE can only generate one request task at most;that is,there is a certain probabilityPr(t) of generating a request task.According to C5,all request tasks must be completed under a predefnied deadline.The number of allocated computation densities(CPU cycles)for executing the request task is less than the maximum capacity (achievable CPU cycles)of the corresponding edge server in C6.

IV.MADRL-BASED COMPUTATIONAL OFFLOADING AND TASK MIGRATION SCHEME

Lemma 1(Optimization problemP1in (18) is NP-hard under constraints C1-C6).

Proof.We can see that problemP1in(18)is a mixedinteger programming that is diffciult to tackle which involves the select variableωr,nand 0-1 integer variableωr.Furthermore,we assumeωr,nis known,the residual sub-problem is a quadratic problem with 0-1 integer under constraints C1,C3-C6,which is a nondefniite matrix.0-1 programming problem is a typical and widely recognized NP-hard problem[34,35].It can be seen that subproblem is a NP-hard problem without considering the optimization variableωr,nunder constraints C1,C3-C6.

Therefore,P1is a NP-Hard vexed question under constraints C1-C6.

This problem commonly reformulated by specifci relaxation approach and then solved by powerful convex optimization techniques.However,P1is considered a multi-MWE cooperation and competition problem.To addressP1,we propose a MADRL-based computation offloading and task migration scheme.

4.1 MDP Model

First,we transit the computational offloading and task migration problem to the MDP,and each MWE is considered a learning agent.

4.1.1 State Space

In terms of the request tasksre,cfrom the MWEe,the state in time slottincludes the arrival probability of the request tasksre,c,the size of the request tasksre,c,the priority of the request tasksre,c,the length of buffer queue on edge servern,the channel state between MWEeand edge servern,the service caching hosted by edge servern,and the changing rate of capacity of edge serverλc.

4.1.2 Action Space

The actionae(t)∈Ais composed of the migrating decision and migrating or offloading selection,which can be written by,

The agent chooses actionae(t)for each request taskre,cfrom MWEeand transits to the next state.

4.1.3 Reward Function

From(18),we consider the optimization problemP1and the limitation conditions C1 ∽C6.We can see thatP1is the global optimization scheme for request tasks of all MWEs.However,we defnie the immediate rewardre(t) as the reward indicate functionD(-aΓe-b)for the request taskre,cof MWEe,wherea,bare the constant coeffciients for the reward function.

Γis the long-term weighted average cost for request taskre,cof MWEeduring the whole periodT.Accordingly,the maximum rewardre(t) can be considered the minimum weighted average cost for executing the request tasksre,cfrom the MWEe.

4.2 Minimizing Cost Scheme Based on MADDPG

The trouble faced by traditional single agent DRL algorithms such as DQN and DDPG is that since each agent can constantly learn and train to improve its optimal policy,from the perspective of each agent,the environment is dynamic and time-varying,and traditional DRL has diffciulty meeting convergence conditions.

MADDPG is essentially a variant of the DDPG algorithm that trains the critic network that requires global information and an actor network that requires local information for each agent and allows each agent to defnie its own reward function,so it can be used for cooperative tasks or competing tasks[36].MADDPG algorithm has three advantages: 1) Centralized training,but distributed execution;2)Improved experience replay of samples;3) Use a policy ensemble to optimize performance.

Therefore,using the advantage of centralized training and decentralized execution for MADDPG,we propose a MADDPG-based computation offloading and task migrating decision-making scheme(MBOMS) for minimizing the long-term average weighted cost in our proposed multi-MWEs MEC framework environment.

We defnie the policy parameters and the policy of the MWE agent asυ=[υ1,υ2,...,υe] andπ=[π1,π2,...,πE],respectively.The expected cumulative rewards of agentecan be derived by

Agentecan observe the joint state from environment composed of the states and the actions of all MWE agentsx=(o1,o2,...,oE),namely,the global observation isx,and the joint action is defnied asa=(a1,a2,...,aE).Because the selection of action follows the deterministic policy,the deterministic policy gradient of agenteis

whereoeis the observation of the agente.is the centralized state-action function of agente.Since each agent learns its own state-action functionindependently,the reward function of each agent is different.Merbstands for the experience replay buffer of all agents,and each sample inMerbis defnied as the tuple〈x,x′,a1,a2,...,an,r1,r2,...,rn〉.

In terms of the value-based critic,inspired by the time difference(TD)and target network of DDQN,the loss is calculated by the mean squared error(MSE)as follows:

For the critic,the gradient can be updated by

In terms of the T-network’s parameters,after certain time period,MADDPG can copy parameters from Enetwork to T-network for each agent of actor and critic as follows:

As shown in Figure 2,the proposed MADDPGbased framework includesEagents.Each agent can interact with the proposed MEC environment,which is similar to the agent of DDPG when execution.However,when training the neural networks of MBOMS,centralized learning methods are utilized to train all critic networks and actor networks.For instance,during the centralized training process,agentecan observe the joint state from environment composed of the states and the actions of all MWE agentsx=(o1,o2,...,oE).During the time slott,the observed statexis input into the actor network of agente;then,the output of the actor network is the local optimal actionaeby the local policy.To this end,the immediate rewardrecan be obtained from the environment and transits to the next observationx′based on the joint actiona.The minibatch transition samples can be stored in the experience replay buffer.Furthermore,the chosen local actiona′e=υe(oe),the global observationx,and the joint actiona={a1,a2,...,aE}are input to the critic network of the agente.In the critic network,each agent can update the state-action functionQυeby training separately.The actions of the other agents can be obtained by interacting with the stationary environment due to offline processing.We can see that the centralized training of the proposed MBOMS algorithm can be convergent and address the unstable environment caused by the different actions of decentralized multiagent algorithms.When executed,each agent can only observe the local state from the actor network and execute the local action with no information of other agents.

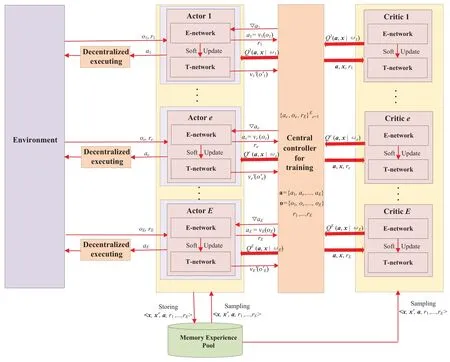
Figure 2.Structure of the proposed MBOMS.

As illustrated in Figure 2,MBOMS can be described in Algorithm 1.First,the parameters used in MBOMS are initialized.Episodes are defnied to better learn the optimal offloading and migrating policy,and one episode includes the whole time periodT.

4.3 Complexity Analysis

For MADDPG-based task offloading service migrating scheme of proposed MBOMS,in terms of each WMEe ∈Ein each group,the neural network for MADDPG is composed ofLk+1 layers: an input layer,Lk-1 fully connected layers,and an output layer.We assume thatMis the number of training samples.Pedenotes the number of Epoch for computing the loss function.nIrepresents the dimension of input layer which is related to the size of state space.From (??),the size of state space iswhere |N| is the size of MEC server,is the size of service cachings hosted by MEC servern.nlis the number of neurons in layern,wheren ∈N,n ≥2.nlis the number of neurons in layern,wheren ∈ N,n ≥2.nOrepresents the dimension of output layer which is related to the size of action space.Therefore,the computation complexity of the proposed MBOMS isO(E×M×Pe×nI×(Lk-1)nl×nO).In addition,we ignored the complexity of all activation functionO(nl),which is only related tonland far less than the complexity of input layer,hidden layer,and output layer for MBOMS.

V.NUMERICAL SIMULATION RESULTS

In this section,we describe in detail the convergence and effectiveness of the proposed MADDPG-based offloading and migrating algorithm in a multi-MWE MEC framework via extensive simulations.

5.1 Simulation Setup

The main simulation parameters are listed in Table 2.In addition,for priorities 1,2,and 3 of request tasks,the arrival probability is set as [1/3,1/3,1/3].The service cachings hosted by each edge server are round robin varying in 100 episodes;that is,during one epoch (overall episodes),service cachings hosted by each edge server will change 10 times.The channel transition probability matrixAn,cis set as the same probability.The channel state vector is set asSchannel=sc* 28* 109,wheresc=[1,2,3,4,5,6,7,8,9].The size of request tasks is set asU～[1,5] Mb.The powers for allocation,transmission for MWEe,and edge servernare all set as 30 dBm.κnis set as 2*10-28.The coeffciients for indicator functionDare set asa=1,b=0.

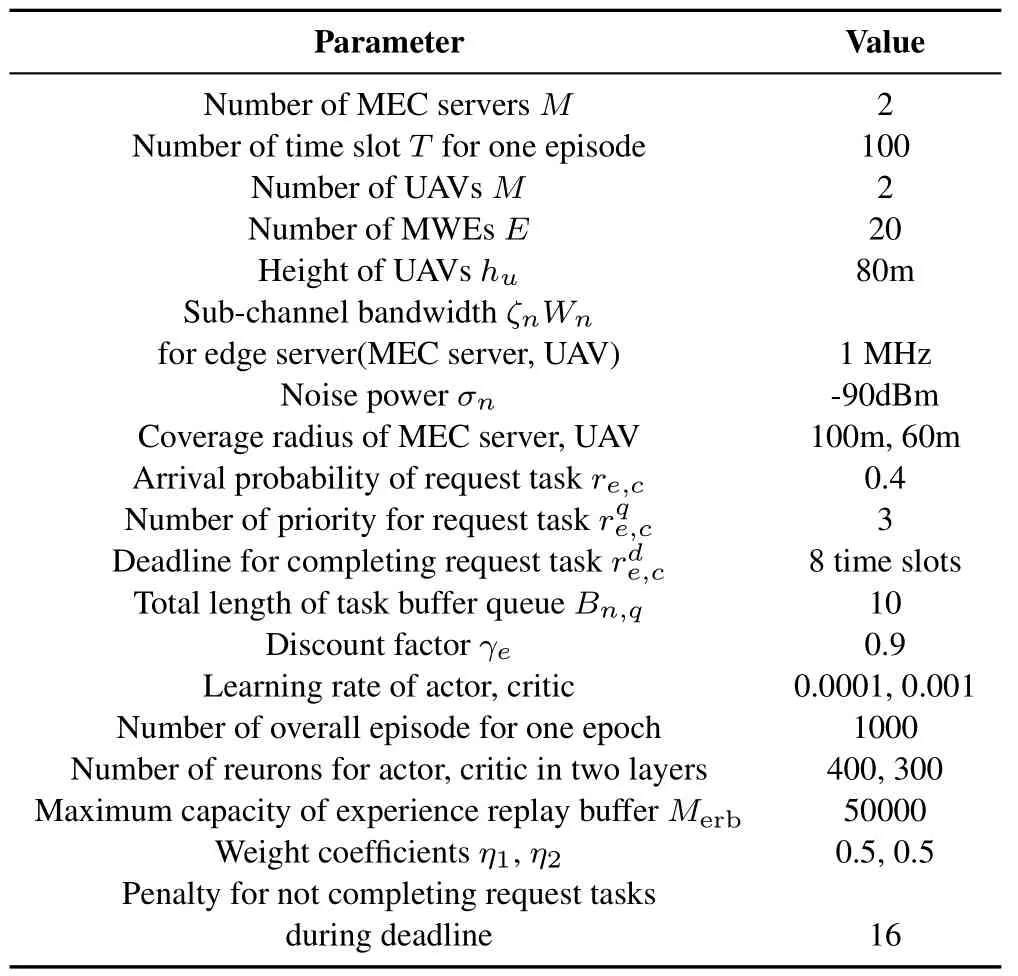
Table 2.Simulation parameter list of the proposed algorithm.

The structures of the E-network and T-network for the actor network and critic network are two layers of fully connected networks.

5.2 Performance Comparison

Five benchmarks are introduced to evaluate and verify the performance of the proposed MADDPG-based offloading and migrating algorithm,which are defnied as:1)Decentralized DDPG-based scheme(DDBS);2)MADDPG-based scheme without migration(MBSM);3) Centralized DDPG-based scheme (CDBS);4) Decentralized DDQN-based scheme (DDQN);5) Centralized scheme based on Q-Learning(Q-Learning).

5.3 Simulation Results

The goal of our work is to minimize the weighted average cost (maximize the expected cumulative reward)by fniding the optimal offloading and migrating decision-making policy.First,we evaluate the convergence of our proposed MBOMS algorithm by the average expected cumulative reward during overall time periodTper episode,which is defnied as

Figure 3 reveals the convergence of MBOMS with different learning rates of criticαcin terms of the average expected cumulative reward per episodeRAPE.Whenαc=0.1,MBOMS works poorly and cannot be convergent because the change in the learning step is too great.If the learning rate is set asαc=0.01,MBOMS can converge well according to the green curve.However,the learning curve fluctuates too much,especially after 800 episodes.Whenαc=0.001,the convergence and performance of MBOMS is better than that when the learning rate is set to other values.

Figure 3.Convergence of MBOMS with different learning rates of critic.

Figure 4 shows the performance of MBOMS in terms of the average expected cumulative reward per episodeRAPEwith different arrival probabilitiesProf request taskre,c.The average expected cumulative reward per episodeRAPEis signifciantly decreased with an increase inPr.However,the convergence of MBOMS can be guaranteed with different confgiurations for probabilityPr,which proves the robustness of our proposed MBOMS.The greatPrmakes the number of request tasks generated by MWE dramatically grow,which leads to the massive penalty during the overall time periodTin each episode.

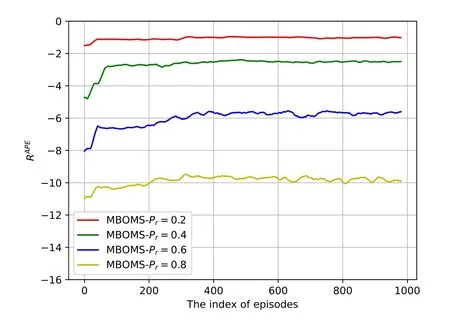
Figure 4.Convergence of MBOMS with different arrival probabilities of request tasks.

Figure 5 illustrates the performance and convergence of six algorithms considering the average expected cumulative reward per episodeRAPE.We can see that the six algorithms can be convergent after several episodes,but the performance is dramatically different.However,the performance of MBOMS is better than that of DDBS,MBSM,and CDBS.Thanks to the decentralized learning pattern,DDBS can gain a better performance,but the average expected cumulative rewardRAPEsignifciantly fluctuates and becomes unstable compared with our proposed MBOMS.Due to no migration for all request tasks,RAPEof MBSM is less than that of MBOMS and DDBS,although the migration cost of MBOMS is great.The performance of CDBS is worst because the centralized training and execution,especially the massive number of requests,works from MWEs.

Figure 5.Convergence of different algorithms.

To evaluate and verify the robust performance of MBOMS,we illustrate the different capacities of edge servers in terms of different priorities of request tasks.Figure 6(a) assumes that the capacity of edge servers(MEC servers and UAVs) is 40.5 GHz.Beneftiting from task migration among the edge server,the unfniished ratio of MBOMS is less than that of MBSM regardless of the priority of request tasks in Figure 6(b).When capacity of all edge servers is set as 30.5 GHz,the number of unfniished request tasks increases slightly.However,the performance of MBOMS is better than that of MBSM considering the unfniished tasks ratio.As shown in Figure 6(c),when the capacity of edge servers (MEC servers and UAVs) is normal but the number of MWEs is set as 30,the number of dropped request tasks will violently increase due to insuffciient CPU cycles for massive tasks of MWEs.However,in terms of all request tasks with different priorities,the unfniished ratio of MBSM is still less than that of MBSM,and task migration is more important for completion under the most stringent deadline.

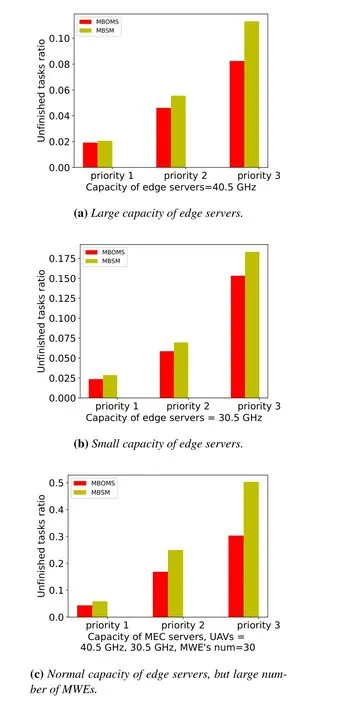
Figure 6.Average unfinished ratio of request tasks with different priorities.

Furthermore,we will compare with fvie other algorithms (DDBS,MBSM,CDBS,DDQN,and QLearning) to verify and confrim the advantages and effectiveness of our proposed MBOMS algorithm.We defnie the mean of expected cumulative rewards of all agents during overall episodes to simulate the negative weighted average cost of the MEC system,which is written as

Figure 7 depicts the mean of expected cumulative rewardsRMOEof the six algorithms with different numbers of MWEsE.WhenE ≤20,the bandwidth and computational resources are suffciient to execute the offloaded request tasks from these MWEs,and theRMOEof the six algorithms does not change signif-i cantly.However,whenE ＞20,because the massive MWEs will generate more request tasks,which increases the burden of edge servers and leads to the massive penalty for unfniished tasks,RMOEdecreases dramatically.

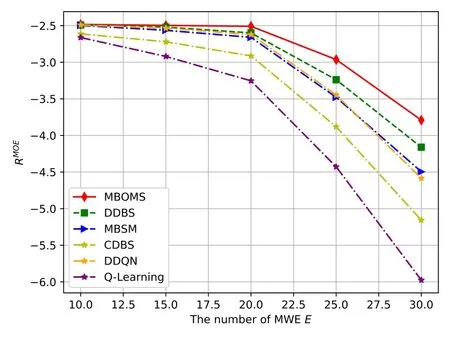
Figure 7.Comparison results with different numbers of MWEs.

Figure 8 illustrates the relationship betweenRMOEand the maximum capacity of the MEC server.According to the maximum capacity of the MEC server shown in axisx,the value of UAV corresponding to the edge server is set as [20.5,25.5,30.5,35.5,40.5]GHz.We can see from the curves in Figure 8 that as the capacity of the edge server increases,RMOEgrows gradually due to the suffciient computation ability of the edge server.In terms ofRMOE,MBOMS outperforms DDBS,MBSM,CDBS,DDQN,and QLearning.When the capacity of MEC server is less than 35.5 GHz because of the competition of computational resources from the MEC server among offloaded request tasks,the performance of DDBS,DDQN are signifciantly worse than those of MBOMS and MBSM.However,the capacity of the MEC server grows gradually,and the performance of DDBS,DDQN are close to those of MBOMS and MBSM.Nevertheless,MBOMS has the best performance.QLearning has the worst performance due to its lack of learning and great Q-Table.

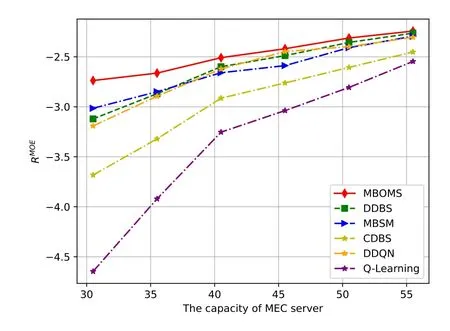
Figure 8.Comparison results with different maximum capacities of the MEC server.

The channel vector is an important factor that can influence the channel gain and uplink available transmission rate between the MWE and edge server.Figure 9 shows the effect of channel vectorSchannelbetween MWEeand edge servernfor the mean of expected cumulative rewardsRMOEof the six algorithms.The greater the channel vectorSchannelis,the greater the uplink available transmission rateWhen the index of channel vectorx ＜8,the lower transmission rate causes greater transmission latency and wait latency in the task buffer queue.Therefore,there are more unfniished request tasks under the deadline,which results in worse performance of the six algorithms.AlthoughRMOEincreases as the index of channel vectorx ＞8,our proposed MBOMS achieves the best performance because of the cooperative training pattern.

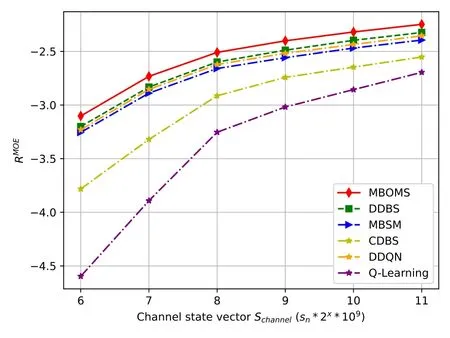
Figure 9.Comparison results with different channel vectors.

VI.CONCLUSION

In this paper,we design a three-tier architecture MEC system assisted with service caching and propose an MADDPG-based computation offloading and task migrating decision-making scheme,named MBOMS.Based on MBOMS,the long-term average weighted cost of the overall MEC system can be minimized by training the neural networks.MBOMS is a robust centralized training and decentralized executing algorithm that considers the randomness of the request tasks generated by the MWE,the time-varying channel between the MWE and the edge server,the changing capacity of the edge server,and the different priorities of request tasks.In the simulation results,the convergence and effectiveness of MBOMS are systematically and comprehensively evaluated and verifeid.

ACKNOWLEDGEMENT

This work was supported by Jilin Provincial Science and Technology Department Natural Science Foundation of China (20210101415JC) and Jilin Provincial Science and Technology Department Free exploration research project of China(YDZJ202201ZYTS642).