基于PCA-MSSA-BP神经网络的列车车轮踏面磨耗预测模型

王冬 杨钰鑫

基金项目：国能铁路装备有限责任公司包头车辆维修分公司研究项目（TZKY-21-45）

第一作者简介：王冬（1984-），男，工程师。研究方向为车辆检修运用。

*通信作者：杨钰鑫（1998-），男，硕士研究生。研究方向为机车车辆测控技术及故障诊断。

DOI：10.19981/j.CN23-1581/G3.2024.12.012

摘  要：分析列车车轮踏面磨耗，预测车轮剩余寿命，对降低车辆运营成本、提高运行安全品质具有重要意义。该文以某公司某型车为例，分析轮对历史检修数据，建立基于PCA-MSSA-BP神经网络的车轮踏面磨耗模型，与传统方法相比，预测精度更高、速度更快。该文首先用主成分分析法从众多磨耗影响因素中提取4个主成分因子，接着建立BP神经网络模型，并针对麻雀优化算法进行改进，验证改进效果，将改进后麻雀算法对网络权值和阈值进行优化，实验结果表明，轮径磨耗、轮缘厚磨耗预测的平均绝对误差分别为0.193 5、0.121 5 mm。

关键词：车轮；磨耗预测；主成分分析；麻雀算法；BP神经网络

中图分类号：U270.33      文献标志码：A          文章编号：2095-2945（2024）12-0049-06

Abstract： It is of great significance to reduce vehicle operation cost and improve operation safety quality to analyze train wheel tread wear and predict wheel residual life. Taking a certain type of car in a company as an example， the historical maintenance data of wheel sets are analyzed， and the wheel tread wear model based on PCA-MSSA-BP neural network is established. Compared with the traditional method， the prediction accuracy is higher and the speed is faster. In this paper， four principal component factors are extracted from many wear influencing factors by principal component analysis， and then the BP neural network model is established. The improved sparrow optimization algorithm is improved and the improved effect is verified. The improved sparrow algorithm is used to optimize the network weight and threshold. The experimental results show that the mean absolute errors of wheel diameter wear and flange thickness wear are 0.193 5 mm and 0.121 5 mm respectively.

Keywords： wheel; wear prediction; principal component analysis; sparrow algorithm; BP neural network

輪对是轨道列车安全运行的重要部件之一，在车辆承载、导向、牵引和制动过程中均发挥着关键作用，其状态好坏会直接影响列车的安全可靠服役。同时轮对也是列车重要的易耗品，数量多、消耗大、检修和更换频繁。列车运行时，车轮与轨道直接接触，两者相互作用产生轮轨力，造成车轮的磨耗和损伤。随着运行时间的增长，轮轨间动态作用会逐步加剧，车轮的磨耗和损伤情况会愈加严重，若没有及时发现处理容易引起尺寸超限，进而影响安全性和平稳性能[1-3]。

目前，车轮踏面磨耗预测方法主要有2种。其一是基于动力学仿真模型，研究列车动力学与相关物理量，采用仿真软件建立模型，模拟列车的真实运行状况进而得到磨耗数据，并与实际磨耗数据对比计算其准确率[4-6]。2012年，Ignesti等[7]提出一种联合模型，该模型包括仿真车辆模型和轮对磨耗模型2部分，通过2个模型交替工作，模拟轮对磨耗的演变过程。2014年，Innocenti等[8]对线路状况进行全面考虑，在FASTSIM程序和磨耗模型基础上，利用SIMPACK软件建立轮对模型，实现对复杂线路下车轮踏面的磨耗预测。2021年，王红兵等[9]利用UM和MATLAB建立了一种更为全面的车轮踏面磨耗预测模型，该模型涵盖了磨耗计算模型、轮轨局部接触模型与车-轨系统耦合动力学模型3部分。其二是基于历史检修数据，利用大数据分析磨耗规律[10-11]，随着数据挖掘、机器学习、深度学习等技术的兴起，该方法逐渐被广泛使用。2014年，邢宗义等[12]针对支持向量机参数优化问题，采用粒子群算法，构造出粒子群优化支持向量机（PSO-SVW）轮对尺寸预测模型，该模型在轮径值预测方面相关度达到0.94，其在轮对尺寸预测方面具有可行性。2020年，张佳文[13]将自适应进化差分算法与最小二乘反向传播神经网络相结合，建立了一种新的用于车轮尺寸数据的预测模型ADE-LMBP，通过与BP神经网络、LMBP神经网络等进行对比实验，验证了该模型在轮对踏面磨耗预测方面的准确性。2022年，王美琪等[14]提出一种基于恒等映射多层极限学习机（I-ML-ELM）的高速列车车轮踏面磨耗测量方法，利用I-ML-ELM模型对车轮踏面磨耗量进行学习及预测，并与真实测量进行对比验证，结果表明，基于I-ML-ELM的预测模型能很好地反映不同参数对车轮踏面磨耗值的影响规律。

受过往检修过程中轮对磨耗数据缺失、丰富程度不足等影响，现阶段基于大数据驱动方法的车轮踏面磨耗预测研究仍相对较少，还是以传统的车辆动力学理论和模型为主，且车体数据越完善，模型准确度越高，但计算量也相对较大。同时目前被广泛用于轮对踏面磨耗预测研究的神经网络模型如多层感知机、BP神经网络等，其模型本身的泛化能力差，训练速度慢，需进一步开展优化列车轮对踏面磨耗预测的神经网络算法研究，提高预测精度和效率。文章构建了基于PCA-MSSA-BP神经网络的列车车轮踏面磨耗预测模型，对轮径磨耗、轮缘厚磨耗2个参数进行拟合预测，有助于更好地监测掌握车轮状态，帮助工作人员合理制定维修计划，对提高检修效率，降低运营成本也具有重要意义。

1  传统方法

本传统方法往往根据检修时测得的轮径数据和检修经验，计算车轮轮径和轮缘厚度磨耗率[15]。车轮轮径磨耗率和车轮轮缘厚磨耗率计算公式分别为

式中：Ｄ１为车轮轮径磨耗率，mm/10 000 km；d1为上次镟后轮径值，mm；d2为下次镟前轮径值，mm；Ｄ2为车轮轮缘厚磨耗率，mm/10 000 km；r1为上次镟后轮缘厚值，mm；r2为下次镟前轮缘厚值，mm；L为运行里程，10 000 km。

根据公式（1）、（2）计算出某公司某型车车轮直径和轮缘厚磨耗速率，具体计算结果如图1、图2所示。

图1輪径磨耗速率

图2轮缘厚磨耗速率

2  基于PCA-MSSA-BP神经网络的预测模型

2.1  主成分分析及BP神经网络

主成分分析法（Principal Component Analysis，PCA）[16]是一种常用的降维方法，可将多种变量数据转化为少数几个彼此互不相关的主成分[17-18]。

PCA的计算步骤如下。

步骤一，初始样本矩阵标准化。

步骤二，计算标准化后样本相关阵。

步骤三，求取特征向量和特征值。

步骤四，计算贡献率与累积贡献率。

步骤五，选择m个主成分，综合评估。

初始样本数据在经过变换之后，新的数据样本通常与初始样本数据存在某种线性组合关系。本文在进行主成分提取时的标准为主成分因子累积贡献率大于80%。

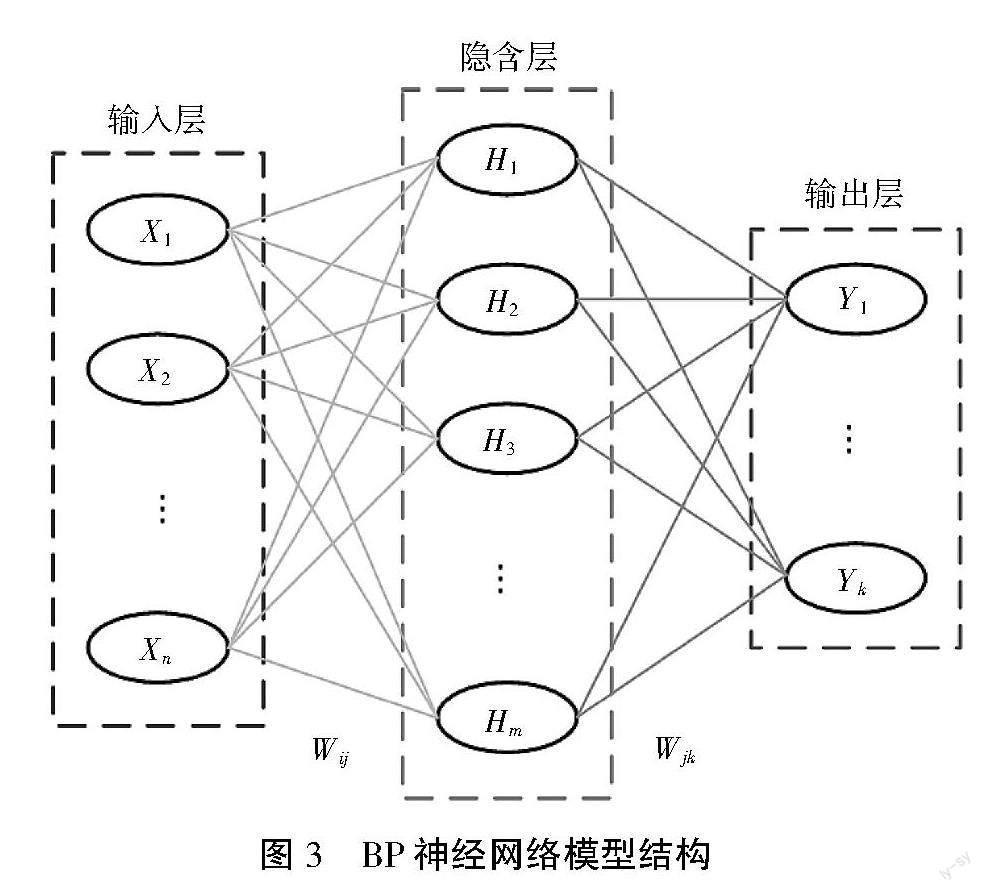
BP神经网络是一种常用神经网络模型[19-20]，其模型结构如图3所示。

BP神经网络结构主要含输入层、输出层、隐含层3部分，其中隐含层的层数可以根据模型要求而调整。

图3BP神经网络模型结构

2.2  改进麻雀搜索算法

麻雀搜索算法（Sparrow Search Algorithm，SSA）是一种模拟群体动物行为的群智能优化算法，其核心思想与人工蜂群算法、POS算法、蚁群算法等类似[21]。SSA的提出受麻雀觅食行为和反捕食行为的启发，其将麻雀的群体行为分为发现者、加入者、侦察者[22-23]，具体行为导则如下。

步骤1：在SSA中，适应度值高的麻雀是发现者，其负责更大的觅食搜索区域，在搜索时会优先获取食物，而加入者为寻找觅食方向会向发现者靠拢。

步骤2：在觅食过程中，发现者附近的加入者可能会与其争夺食物，这是加入者为提高自身捕食率而产生的行为，因此发现者和加入者的身份可能会随时转变，但是两者在种群内的比重是保持一定的。为了获得更多的能量和找到更好的发现者，部分饥饿的加入者会前往其他区域进行觅食。当预警值超过预先设定上限值时，表示麻雀种群意识到危险，此时种群中间的麻雀会随机行走，以靠近邻近麻雀，而处于边缘的麻雀会迅速移动调整以获得更安全的位置，上述过程即为麻雀种群的反捕食行为。

文章针对麻雀算法中存在的部分不足进行优化，具体改进如下。

2.2.1  改进二维Logistic混沌映射策略

麻雀搜索算法中初始参数的均匀性程度会显著影响最终结果。原始麻雀搜索算法参数初始化采用随机函数进行，初始值的均匀性和多样性无法很好地得到保证。本文提出利用改进二维Logistic混沌映射策略进行初始化[24]，其映射公式如下

式中：xn、yn为混沌序列值；sin（x）为正弦函数。当a∈[0，1]时，该系统处于混沌状态。

确定上述映射策略后，再通过下式将序列值赋给种群初始化个体

x（i）=lb+（ub-lb）×y（i） ， （5）

式中：[lb，ub]为个体搜索区间；x（i）为个体位置；y（i）为混沌序列。

此时生成的种群初始化值将具有均匀、遍历的特点。

2.2.2  多向学习策略

原麻雀搜索算法中，加入者位置更新时，每次只选择一个最佳个体进行学习，这种方式对快速搜索最佳位置有利，却在一定程度上降低搜索的多样性，使得最终结果易陷入局部最优。针对此，采用多向学习策略对加入者位置更新公式进行优化[25]，新的加入者位置更新公式如下

，    （6）

式中：pa、pb、pc分别为a、b、c三个个体权重；a为最优解；b、c分别为与a不同的随机解。

计算公式如下

（7）

式中：Fa为个体a的适应度值；Fb为个体b的适应度值；Fc为个体c的适应度值。

根据适应度值来计算权重，针对适应度值更小的个体给予更大的权重，适应度值较大的个体分配较小的权重，这样综合考虑3个麻雀个体的信息，以扩大搜索空间。

2.2.3  遗传算子变异操作

为避免算法陷入局部最优，引入遗传优化算法中的变异算子，对麻雀种群中的最优个体进行变异操作，从而提升全局搜索能力。

对最优个体xi随机产生p∈[0，1]进行变异，变异公式如下

式中：wi为区间[lb-xi，ub-xi]上的随机数，从而使得xi变异后仍在搜索区间上；pm为变异概率，变异概率计算公式如下

pm=0.03+0.51-■，（9）

式中：tmax为最大迭代次数；t为本次迭代次数。

以上为针对SSA算法的改进。验证改进后算法的寻优效果与改进前作比较，结果如图4所示，不难看出，200次的迭代次数下，改进算法展现出了优于原始算法的性能。

2.3  PCA-MSSA-BP神经网络

正BP神经网络存在初始化参数影响大、学习效率低、易过度拟合和收敛慢等问题。采用改进麻雀算法优化BP神经网络的初始权值和阈值。

整个预测模型流程如图5所示。

实验步骤如下。

步骤1，数据处理。对车组数据进行预筛选，选择有效数据作为初始样本数据，利用主成分分析法进行数据降维处理。

步骤2，建立BP神经网络初始模型。根据数据降维处理结果去确定网络的输入量和输出量，选择各网络层层数，初始化网络参数。

步骤3，种群初始化。确定网络参数个数，依次对个体编码，本文适应度函数为绝对误差，每个个体的适应度值计算如式（10）

式中：n为总预测数据；yi为实际输出；hi为预测输出；F为个体适应度。

步骤4，划分发现者、加入者并更新位置，选择侦察者并更新位置。

步骤5，参数优化。在允许迭代次数内且预测值与真实值之差满足误差阈值时，输出最优个体。

步骤6，网络优化。在进行网络训练和预测前，将麻雀算法优化后的权重与阈值重新分配给BP神经网络，进一步优化模型。

图5  PCA-MSSA-BP算法流程

3  實验与分析

本文以某公司某车型为例，整理筛选检修数据9 472组，得到上次镟后轮径值、上次镟后轮缘厚、同轴轮径差和运行里程等8个影响参数，利用PCA进行降维，得到4个主成分因子，作为网络模型输入。设置MSSA-BP神经网络的结构为4-10-2，即4个输入层、10个隐含层、2个输出层，输出层分别为轮径、轮缘厚的磨耗值。本文网络模型含12个阈值，各层连接为全连接则共有60个权值。分别选择tansig和purelin作为MSSA-BP神经网络的隐含层和输出层激励函数，选用traingd作为训练函数，最小目标误差阈值为0.1，学习率为0.01。种群数目与进化代数分别为20个、200次，发现者占比20%，加入者占比80%。

对MSSA-BP神经网络进行训练、预测，结果如图6、图7所示。

图8为PCA-MSSA-BP神经网络预测模型中麻雀算法迭代200次的适应度变化图，从图8中可以看出，该模型的误差随着算法的优化显著降低；模型的最优参数出现在适应度降至最小值时，此时模型迭代了约80次。

图6轮径磨耗预测误差

图7  轮缘厚磨耗预测误差

图8  PCA-MSSA-BP神经网络模型适应度变化曲线

为验证模型作用，选取传统方法和BP神经网络模型的预测结果与其作比较，用均方根误差（RMSE）及平均绝对误差（AE）衡量预测效果，AE公式为式（10），RMSE计算公式如下

RMSE=■，（11）

式中：n为预测数据量；hi为预测值；yi为实际值。

根据公式（10）、（11）及模型预测结果，计算结果对比见表1。

表1  不同方法的预测结果

由表1可知，相对传统算法，PCA-BP神经网络在轮径磨耗预测方面误差没有明显降低，但轮缘厚磨耗预测精度得到明显提升，RMSE下降明显、AE略低于传统方法；经过麻雀算法对模型进行优化，PCA-MSSA-BP神经网络预测模型在轮径磨耗预测和轮缘厚磨耗预测的误差均明显降低，最终2个参数预测的平均绝对误差分别为0.193 5、0.121 5 mm。

改变训练和预测数集，对最终模型进行重复训练、预测，结果见表2。

表2  PCA-MSSA-BP神经网络稳定性检验

由表1、2可知，将改进麻雀算法引入BP神经网络有明显的优化作用，且该算法自身稳定性较高。该轮对踏面磨耗预测模型能对踏面磨耗实现较准确的预测，可进一步用于车轮剩余寿命预测及镟修计划编排，具有现实意义。

4  结论

本传统车轮磨耗分析方法，只考虑了踏面参数变化，未考虑到其他因素对踏面磨耗的影响。本文利用某型车检修数据，对车轮踏面磨耗进行研究，最终建立PCA-MSSA-BP神经网络模型，实现踏面磨耗预测，对延长车轮使用寿命、进行车轮全寿命周期监控、降低轮对运维成本具有重要意义。

参考文献：

[1] 曾元辰，唐旭，张卫华，等.车轮尺寸对车轮磨耗的影响规律研究[J].铁道学报，2022，44（4）：27-35.

[2] 张卫华，李权福，宋冬利.关于铁路机车车辆健康管理与状态修的思考[J].中国机械工程，2021，32（4）：379-389.

[3] WANG X P， MA H， ZHANG J. A Prediction Method for Wheel Tread Wear[J].Industrial Lubrication and Tribology， 2019，71（6）：819-825．

[4] 顾正隆，葛亦凡.基于轮对磨耗数据数理统计的轮对镟修策略多目标优化[J].城市轨道交通研究，2021，24（S1）：21-25，30.

[5] 张渝，王松，邱春蓉.基于轮对磨耗数据的CRH2A型动车经济镟修策略研究[J].铁路计算机应用，2021，30（4）：6-10.

[6] SHI H M， YANG J S， SI J. Centralized maintenance time prediction algorithm for freight train wheels based on remaining useful life prediction[J].Mathematical Problems in Engineering， 2020（2020）：1-12.

[7] IGNESTI M， MARINI L， MELI E， et al. Development of a wear model for the prediction of wheel and rail profile evolution in railway systems[J]. Wear， 2012，284-285（1）：1-17.

[8] INNOCENTI A， MARINI L， MELI E， et al. Development of a wear model for the analysis of complex railway networks[J]. Wear， 2014，309（1-2）：174-191.

[9] 王红兵，李艺，李国芳，等.高速车辆车轮踏面磨耗预测及系统参数影响分析[J].机械科学与技术，2022，41（5）：786-794.

[10] 吴健，叶正君，邢宗义.城市轨道交通列车轮对磨耗模型研究[J].铁路计算机应用，2020，29（2）：62-67.

[11] 韩鹏，张卫华.高速列车轮对磨耗统计规律及预测模型[J].机械工程学报，2016，52（2）：144-149.

[12] 邢宗义，冒玲丽，廖贵玲，等.基于PSO-SVM模型的城轨列车轮对尺寸预测[J].沈阳工业大学学报，2014，36（4）：411-415.

[13] 张佳文.基于神经网络的高速列车轮对尺寸预测及镟修策略研究[D].成都：西南交通大学，2020.

[14] 王美琪，王艺，陈恩利，等.基于恒等映射多层极限学习机的高速列车踏面磨耗预测模型[J].力学学报，2022，54（6）：1720-1731.

[15] 田丽，刘森.基于数据拟合的地铁车辆车轮磨耗分析与寿命预测[J].铁道技术监督，2022，50（2）：65-68.

[16] JOLLIFFE I T， CADIMA J. Principal component analysis： a review and recent developments[J]. Philosophical Transactions of the Royal Society A：Mathematical， Physical and Engineering Sciences， 2016（13）：374.

[17] 乔守旭，钟文义，谭思超，等.基于PCA-GA-SVM的竖直下降两相流流型预测[J].核动力工程，2022，43（3）：85-93.

[18] 徐雄，林海军，刘悠勇，等.融合PCA与自适应K-Means聚类的水电机组故障检测在线方法[J].电子测量与仪器学报，2022，36（3）：260-267.

[19] 周永长，黄亚宇.基于BP神经网络建立二次润叶工艺参数的预测模型[J].电子科技，2022，35（9）：79-86.

[20] YAO G X， CHEN G G， PU Z W， et al. Research on vibration fatigue damage locations of offshore oil and gas pipelines based on the GA-Improved BP neural network[J]. Shock and Vibration，2023：18.

[21] 刘美辰，薛河儒，刘江平，等.牛奶蛋白质含量的SSA-SVM高光谱预测模型[J].光谱学与光谱分析，2022，42（5）：1601-1606.

[22] XUE J K， SHEN B. A novel swarm intelligence optimization approach： sparrow search algorithm[J]. Systems Science & Control Engineering， 2020，8（1）：22-34.

[23] TANG A D， HUAN Z， TONG H， et al. A chaos sparrow search algorithm with logarithmic spiral and adaptive step for engineering problems[J].Computer Modeling in Engineering & Sciences， 2022，130（1）：331-364.

[24] 方鵬飞，黄陆光，娄苗苗，等.基于二维Logistic混沌映射与DNA序列运算的图像加密算法[J].中国科技论文，2021，16（3）：247-252.

[25] 柴岩，孙笑笑，任生.融合多向学习的混沌麻雀搜索算法[J].计算机工程与应用，2023，59（6）：81-91.