冗余驱动并联机械手运动精度校准方法研究

张 凯，孙德全，刘石林

（1.郑州旅游职业学院机电工程学院，河南 郑州 451464；2.河南科技大学机电工程学院，河南 洛阳 471000）

1 引言

数控混合五轴加工是解决复杂几何曲面零件的重要途径[1]。并联机器人作为主轴头高质量加工的重要部件，是实现复杂几何零件加工精度的重要保障。与非冗余驱动形式相比，冗余驱动并联机器人（RAPM）通常具有更好的灵巧性、更高的刚度和更好的动态性能等相对优势[2]。采用三自由度RAPM作为主轴头进行高质量加工时，必须保证其运动精度。

近年来，冗余驱动并联机器人引起了学术界和工业界的高度关注。机器人运动精度的校准是实现机器人高运动精度的重要手段。文献[3]根据并联机构逆运动学误差建模理论，提出了一种基于Matlab的数值仿真方法，并采用最小二乘法识别六自由度并联机构的结构参数，通过仿真验证了该标定算法的鲁棒性和有效性。文献[4]采用迭代法对混合运动机床和3-P（Pa）S并联主轴头进行了误差识别，采用非线性最小二乘算法对机构几何参数进行了估计。文献[5]针对六关节机器人的标定方法，提出了五点优选TCP标定优化改进模型，通过该仿真和实验验证了该改进算法在标定精度的有效性。文献[6]在串联机器人单孔标定方法的基础上，通过MDH误差建模提出了多孔标定优化方法，该方法通过实验表明具有较高的定位精度。文献[7]采用粒子群算法对六自由度机械臂关节参数进行了标定，该方法具有较好的收敛性，同样通过实验表明该方法在标定精度提升方法具有一定的优势。文献[8]采用PSO算法对工业机器人的定位精度进行了优化改进，通过建立D-H参数误差模型标定位姿平台两点之间的绝对距离，有效提升了标定精度。文献[9]针对3-R2U2S并联机器人的参数标定，分析了影响机构参数变化的各种误差源，在此基础上建立了机器人运动学误差模型，提出了自动协作原理的参数标定方法，该方法通过实验得到了有效验证。

本研究在前人研究的基础上，提出了基于最小误差模型的运动精度标准方法。首先通过消除冗余几何源误差，建立包含最少几何源误差的最小误差模型，采用蒙特卡罗模拟进行几何源误差灵敏度分析，研究各几何源误差对终端精度的相对影响。在此基础上提出了粗校准和精校准相结合的分层辨识策略，以实现冗余驱动并联机械手的精度校准。最后通过校准实验来验证了所提出校准方法的有效性。

2 冗余驱动并联机械手最小误差模型

2.1 并联机械手运动学模型

本研究的冗余驱动并联机械手模型，如图1所示。其后面的拓扑结构为2UPR&2RPS的RAPM。其中，'U'、'R'、'S'、'P'分别代表万向节、转动关节、球形关节和驱动移动关节。它由一个固定底座、一个移动平台、两个相同的UPR肢腿和两个相同的RPS肢腿组成，主轴头具有三自由度。肢腿1 和肢腿3 为对称分布的UPR肢腿，肢腿2和肢腿4是两个对称分布的RPS肢腿。各肢腿分别与固定基座和移动平台在Ai点和Bi点相连。

图1 三自由度主轴头模型示意图Fig.1 Diagram of Three Degree of Freedom Main Shaft Head Model

定义全局坐标系O-xyz的原点固定在基座平面A1A2A3A4的中心，z轴垂直于该平面，x轴与的向量方向一致，y轴方向是由右手定则决定的。机架坐标系O'-uvw的原点O'固定在移动平台正方形B1B2B3B4的中心，其中w轴垂直于该平面，u轴与--------B2B4的向量方向一致，v轴方向由右手法则决定。参考坐标系O'-x'y'z'位于点O'，其轴线平行于坐标系O-xyz。根据主轴头的结构，可以将'U'或'S'关节分解为多个串行的单自由度关节。根据螺旋理论，在O'点处的扭转可以表示为：

式中：$；ta，j，i—第i肢腿的第j个单自由度关节的单位扭转，其方向与关节轴方向一致；，j，i—'R'关节轴的角速度。

对于UPR肢腿，关节扭矩可表示为：

其中，sj，i—第i肢腿第j个单自由度关节轴的单位向量；、—点Ai和Bi相对于O'-x'y'z'的位置向量。通过找到所有扭力的零内积，可以获得UPR支腿的约束扭转力：

由此可得约束扭矩和驱动扭矩为：

2.2 冗余误差的消除

为了便于误差建模，UPR和RPS肢腿中的所有机身固定关节坐标系，如图2所示。

图2 UPR和RPS肢腿的关节坐标系Fig.2 Joint Coordinate System of UPR and RPS Limbs

Oj，i-xj，iyj，izj，i定义为第i肢腿第j个单自由度关节的机身固定坐标系，其中zj，i轴与关节轴重合，xj，i轴与zj，i轴和zj+1，i轴的公法线重合，Oj，i是zj，i轴和xj，i轴的交点，yj，i轴由右手定则确定。对于每个肢腿，全局坐标系O-xyz被视为第0个关节坐标系，机身固定坐标系O'-uvw被视为最后一个关节坐标系，点Ai与O1，i重合，Bi与点O4，i（i=1，3）重合。

利用上述定义，得到了相邻关节与固定坐标系之间的几何关系，Oj，i-xj，iyj，izj，i相对于Oj-1，i-xj-1，iyj-1，izj-1，i的几何误差可表示为：

其中，［Δxj，iΔyj，iΔzj，i］T和［Δαj，iΔβj，iΔγj，i］T分别表示位置误差和方向误差。如果一个几何源误差依赖于另一个几何源误差，则可以定义为冗余几何源误差。为了简化误差模型，消除几何源误差，本研究提出了消除冗余几何源误差的一般原则［10］：

（1）若第j个单自由度关节为移动关节，则Δzj+1，i为冗余，可合并为零偏移；

（2）如果j-1≠0，则第（j-1）个关节不是移动关节，由于Δyj，i和Δβj，i没有包含在变换中，其为冗余的，Δγj，i可合并为关节运动误差；

（3）如果zj，i轴平行于zj-1，i轴，则Δxj，i，Δαj，i，Δzj+1，i和Δγj+1，i是冗余的，它们可以合并为Δxj-1，i，Δαj-1，i，Δzj，i和Δγj，i。

根据上述原理消除冗余几何源误差后，可得UPR肢腿的几何源误差为：

同样，RPS肢腿的几何源误差表示为

由于O4，i-x4，iy4，iz4，i（i=1，3），O5，i-x5，iy5，iz5，i（i=2，4）相对于O'-uvw的变换矩阵为常数，则较易求解O'-uvw中的Δ5，i（i=1，3），Δ6，i（i=2，4）。

2.3 机械手的误差模型

取式（1）中的一阶摄动，点O'处的误差扭转可以表述为：

其中，$；G，i表示点O'处几何源误差产生的误差扭曲；Δωa，j，i表示关节运动误差，与几何误差无关，表示关节坐标系Oj-1，ixj-1，iyj-1，izj-1，i相对于O'-x'y'z'的变换矩阵。

则式（15）～式（22）以组合矩阵的形式得到：

最后，得到主轴头的最小误差模型为：

式中：Δr、Δθ—2UPR&2RPS 并联主轴头的终端位置误差和方向误差；（的第i列（i=1-4）。

3 几何源误差敏感性分析

本节通过灵敏度分析，筛选出对移动平台精度影响较大的几何源误差，采用误差系数矩阵来表示灵敏度指标。对于矩阵ε的第n行几何源误差δn，终端位置方向精度的灵敏度系数表述为［11-12］：

其中，（Jεa）i，n—误差系数矩阵Jεa的第i行第n列元素，任意给定的几何源误差δn引起的体积位置和方向误差可表述为：

对于主轴头零件的批量生产，几何源误差的值是一个正态分布的随机变量，其均值为0，标准差σ为公差的1∕6。考虑到几何源误差在公差区内的分布，可以采用蒙特卡罗模拟进行灵敏度分析，通过大量的模拟次数分析每个几何源误差的灵敏度。对于单次模拟，δn是由N（0，σ2）随机生成，由此获得整个工作空间V中δrn和δθn的最大值为：

经过N次模拟，获取ηrn和ηθn的最大值，并定义为误差指标为：

根据前述研究，所有几何源误差的公差情况，如表1、表2所示。几何源误差的标准偏差是公差的1∕6。主轴头的工作空间由三个运动变量来表示，分别是绕u轴的旋进角ψ、绕y轴的旋转角θ和沿方向的位移z。主轴头的尺寸参数，如表3所示。la和lb分别为固定底座和移动平台的外径，qmin和qmax表示肢腿的最小允许长度和最大允许长度，θU1和θU2分别为围绕固定底座上U型关节的第一旋转轴和第二旋转轴的允许旋转角，θS1，θS2和θS3分别为连接在移动平台上S关节第一、第二、第三旋转轴的允许转角，θ1R和θ2R分别为与固定基座和移动平台上的R关节的允许旋转角。

表1 UPR肢腿中几何源误差的公差Tab.1 Tolerance of Geometric Source Error in UPR Legs

表2 RPS肢腿中几何源误差的公差Tab.2 Tolerance of Geometric Source Error in RPS Legs

表3 主轴头的尺寸参数Tab.3 Dimensional Parameters of Main Shaft Head

根据给定的尺寸参数，计算2UPR&2RPS并联主轴头的工作空间，如图3所示。

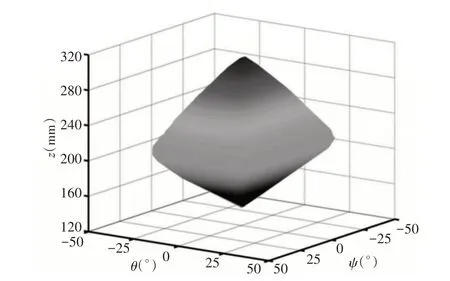
图3 并联主轴头的工作空间Fig.3 Working Space of Parallel Main Shaft Head

计算的工作空间对称于轴ψ=0°和θ=0°，与2UPR&2RPS 平行主轴头的对称结构一致。同时，计算工作空间的最大截面出现在轴ψ=0°和θ=0°，如图4所示，可以看出当ψ=0°和θ=0°时，z的最大量程可以达到（140～310）mm，当z=210mm，ψ=0°时，θ的最大量程范围为（-26～26）°；当z=240mm，θ=0°时，ψ的最大量程范围为（-34～34）°，计算工作区的体积为79.96mm·rad2。

图4 工作空间横截面的计算Fig.4 Calculation of Workspace Cross Section

由于对称分布，两个相同的UPR（RPS）肢腿的几何源误差对终端精度的影响是相同的。由于几何源误差数目较大，为了简便起见，仅选取肢腿1和肢腿2中的几何源误差来描述灵敏度指标。设N=500，通过对[ε1；ε2]中的非零项进行排序，如图5所示。

图5 几何源误差灵敏度指标Fig.5 Sensitivity Indices of Geometric Source Errors

描述了38 个源误差和相应的灵敏度指标。可以看出UPR肢腿中Δα1，i，Δβ1，i，Δγ1，i，Δα2，i，Δα3，i，Δβ4，i，Δγ4，i，Δα5，i，Δβ5，i，Δγ5，i和RPS 肢腿中Δγ1，i，Δβ3，i，Δγ3，i，Δα4，i，Δα5，i，Δγ6，i对终端位置精度和方向精度都有一定的影响，而其他参数的敏感性指数几乎是零值，表明这些参数对终端位置精度和方向精度的影响不大。

4 并联机械手的校准方法

在本研究中，采用AT960激光跟踪仪距离测量装置，如图6所示。

图6 激光反射器安装位置图Fig.6 Installation Position of Laser Reflector

激光跟踪器测量激光反射点Om的位置误差[13]，而不是移动平台的中心点O'，测量的激光反射点Om位于移动平台机身固定坐标系O'-uvw的w轴上。测点位置误差模型Om可以表述为：

式中：em—点Om的位置误差；lm—测点相对于O'-uvw的位置向量，误差系数矩阵Kε与几何源误差相关，误差系数矩阵Kω与零偏移量有关。

4.1 零偏移量的粗识别

利用线性最小二乘法来识别零偏移量，根据测量的终端位置误差，零点偏移量可表述为：

式中：emk—第k次测量的位置误差；Kωk—第k次测量点位置误差模型中与零偏移相关的误差系数矩阵。为了达到更准确的估计，在式（44）的基础上采用迭代算法：

其中，ξ是一个给定的阈值。

4.2 几何源误差的精识别

在对零偏移量进行粗识别后，对几何源误差进行精识别。为了能够便于识别，剔除终端精度影响相对较弱的几何源误差，只保留38个需要识别的几何源误差［14］。采用最小二乘法得到的辨识方程为：

其中，eck—粗校后的第k次测量位置误差；Kεk—第k次测量的点位置误差模型与几何源误差相关的误差系数矩阵。为了使ε可识别，先决条件秩（Hε）≥38必须满足，这可能导致多重共线性问题。为了解决这一问题，引入了正则化方法，即在辨识矩阵中插入正则化参数：

其中，λ是广义交叉验证（GCV）方法定义的正则化参数，ελ为正则化法得到的解，且。

利用上述分层辨识策略，首先可以通过根据辨识出的零偏移调整执行器输出来执行粗识别。然后，根据识别出的几何源误差，对数控系统中的几何参数进行修正，以实现精识别，识别程序的流程图，如图7所示。

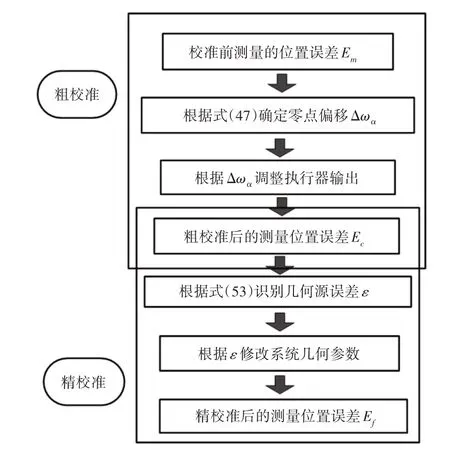
图7 两步识别方法的步骤Fig.7 Steps of Two-Step Calibration Method

5 实验验证

粗识别和精识别的实验装置，如图8所示。三自由度主轴头由四个伺服电机驱动，由数控系统控制。通过将运动数据导入数控系统，可将移动平台调整到目标姿态。在此基础上，利用AT960激光跟踪仪进行校准实验，跟踪激光反射点的位置。在测量规划过程中，测量装置应遍历主轴头的所有自由度，且测量的构型应包括易发生最大位置误差的工作空间边界。

图8 校准实验装置Fig.8 The Experimental Calibration Setup

测量的结构被规划为在三个等距平面上等间距的点，在z=200mm平面上，ψ的范围为（-25～25）°，θ的范围为（-15～15）°；在z=220mm平面上，ψ的范围为（-25～25）°，θ的范围为（-20～20）°；在z=240mm平面上，ψ的范围为（-25～25）°，θ的范围为（-20～20）°。旋转角度的增量步长设为5°。

按照平面z=200mm、z=220mm、z=240mm的先后顺序进行测量。以平面z=200mm为例，测量的顺序，如图9所示。可以看出各坐标轴的位置误差，当θ从-15°增大到15°时，ψ从-25°增大到25°。

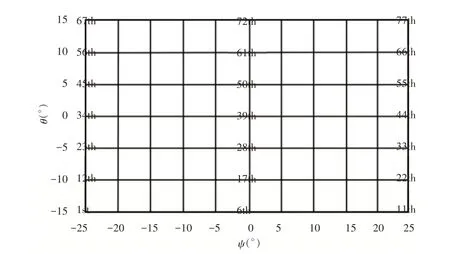
图9 粗校准位置误差的测量Fig.9 Measurement of Coarse Calibration Position Error

由此得到粗校准前后三个坐标轴的位置误差，如图10所示。其中emx，emy和emz分别表示em沿x，y和z轴的误差分量。从图中可以看出，在每个测量平面上，沿各坐标轴的终端位置误差相对于轴θ=0°是对称的。同时，在每个测量平面上，各坐标轴上的位置误差相对于轴ψ=0°是对称。这与2UPR&2RPS平行主轴头的对称结构类似。

图10 粗校准前后的位置误差Fig.10 Position Errors Before and After Coarse Calibration

在粗定标前，位置误差的绝对值是沿每个轴的相邻测量平面之间的步进增量。对于沿x轴位置误差emx，在三个测量平面的误差范围分别为（-100～100）µm、（0～200）µm、（100～300）µm。对于沿y轴位置误差emy，在三个测量平面的误差范围分别为（-25～25）µm、（50～100）µm、（100～150）µm；对于沿z轴位置误差emz，在三个测量平面的误差范围分别为（-50～50）µm、（-100～0）µm、（-150～-50）µm。三个测量平面上各轴上的位置误差分布是相似的，这表明z值的增加导致位置误差幅值的增加，但不影响θ和ψ轴向角构成的平面上的位置误差分布，这表明存在初始位置误差，即主轴头中的零偏移。

粗校准后，沿各轴消除了步进增量，即消除零偏移。沿x轴上的ecx在三个测量平面上的测量范围为（-100～100）µm，沿y轴上的ecy在三个测量平面上的测量范围为（-25～25）µm，沿着z轴上的ecz在三个测量平面上的测量范围为（-50～50）µm。这也表明该方法是有效的。精校准前后各测量平面的误差分布，如图11所示。可以看出上述定义的误差指标既与位置有关，又与方向有关。在每个测量平面上，误差指标始终同时与轴θ=0°和ψ=0°对称，与主轴头的对称结构一致。在精校准前，θ的变化对误差分布的影响比ψ的影响更大。经过精校准后，误差指数和误差波动均得到降低。精定标在θ边界处效果最佳，误差指数大幅度减小。精校准后，ψ的变化对误差分布有较大的影响。

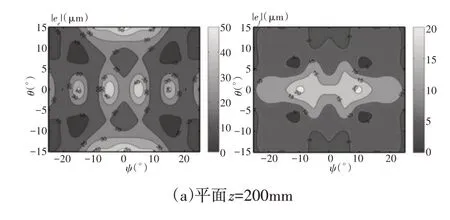
图11 精密校准前后的误差指标Fig.11 Error Indices Before and After Fine Calibration

校准前后各测量平面误差指标最大值和平均值，如表4 所示。可以看出在各测量平面，经过两步校准，误差指数最大值和平均值都得到了大幅降低，这也证明了所提出的两步校准方法的有效性。

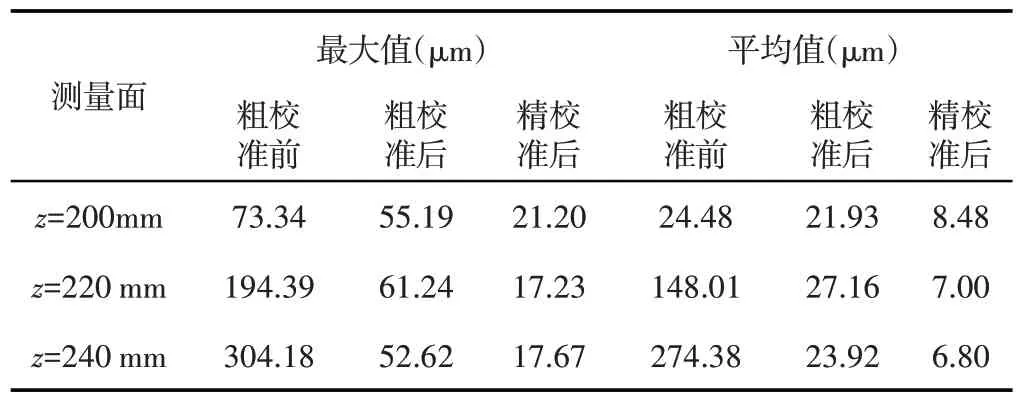
表4 校正前后误差指标的最大值和平均值Tab.4 Maximum and Average Values of Error Indicators Before and After Correction

6 结论

提出了一种基于最小误差模型的并联机械手（RAPM）运动学校准方法。首先基于并联机械手肢腿结构特性和各关节相应的坐标系，提出了一套消除RAPM 中冗余几何源误差的一般原则，推导了解析误差映射公式，将零偏移量与物理意义直观的几何源误差分离。在此基础上提出了一种由零偏移量粗识别和几何源误差精识别组成的分层识别策略，从而实现冗余驱动并联机械手的精度校准。最后通过校准实验测试表明，所提出的校准方法能够大幅降低冗余驱动并联机械手的终端误差，验证了所提校准方法的有效性。该校准方法也适用于其他类型的并联机械手的精度校准，具有一定的普适性。