永磁同步电机无模型自适应滑模补偿预测控制

刘慧博，张 翀，黄前柱

（内蒙古科技大学信息工程学院，内蒙古 包头 014010）

1 引言

由于永磁同步电机（PMSM）具有诸多优点，被应用于各种控制系统，但PMSM同时由于自身的多变量，非线性等缺点使得某些控制方法应用在PMSM控制系统上时难以达到预期效果。例如传统双闭环PI控制器的矢量控制策略，虽然能够达到稳定控制的性能，但是无法使得超调量和快速性同时满足要求[1]。所以随着控制理论的发展，如模型预测控制、自抗扰控制、滑模控制、反推控制以及其他新型控制理论也被推导应用在PMSM控制系统中[2]。其中，模型预测控制理论由于具有超前预测，反馈校正和滚动优化的特点已被广泛地应用在了永磁同步电机控制系统中，此方法使控制系统可以达到较快的动态响应和更高的精度[3]。虽然模型预测控制器能够达到良好的控制性能，但是其结构较依赖于模型参数，易在电机运行过程产生参数失配现象，降低控制性能，为了解决这个问题，文献[4]应用无模型自适应控制策略设计控制器，克服了被控对象模型控制的局限性并有效减少了工作量；文献[5]将无模型自适应控制和预测控制相结合，利用生成的动态线性化模型对系统做预测控制，获得较好的控制跟踪性能。由于无模型自适应控制方法没有反馈校正环节，易受外部扰动的影响，鲁棒性不高[6]。

有文献[7]将无模型自适应控制算法与其他鲁棒性高的控制算法结合，来提升控制的鲁棒性。文献[8]中的无模型自适应控制加入了跟踪微分器，有效抑制了干扰，使系统性能得以提升。实验结果表明，在无模型自适应控制器上加以改进可以克服原本的缺点。文献[9]在无模型自适应控制的基础上增加了滑模补偿项，增强了系统的鲁棒性，但没有克服自身抖振对控制性能的影响[10]。根据以上陈述，针对PMSM模型预测矢量控制系统控制性能受限于电机的数学模型并容易受电机参数变化扰动的问题，提出将无模型预测控制方法应用到PMSM 中，解决电机模型限制和参数失配问题。又由于无模型自适应预测控制方法没有反馈校正环节，易受外部扰动的影响，所以设计高阶滑模补偿器作为校正部分，解决控制系统鲁棒性低和抖振现象。仿真验证了该算法的可行性。

2 模型预测控制参数失配分析

由文献［11］可知，用模型预测算法设计电流环时要用到电机定子电阻和电感参数值，设计转速环时要用到电机磁链参数值，因此用模型预测算法设计永磁同步电机矢量控制系统时离不开电机电磁参数值。但在实际运行工况中，PMSM经常出现不可避免的温升，电机的电磁参数会随着温度的升高发生变化，比如电阻值变大，磁链值减小，电感也会发生变化。如果电机参数变化，控制器参数没有跟着一起改变，就会引起参数失配，参数失配会对系统控制性能造成影响，模拟了电机运行过程中电阻，磁链，电感增大或减小时，模型预测算法设计的控制器参数固定不变和控制器参数跟随改变时的d-q轴电流变化曲线，如图1～图6所示。

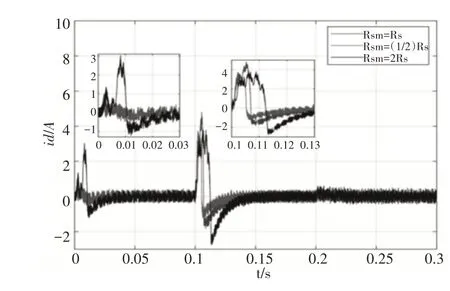
图1 控制器与电机电阻失配和匹配时d轴电流变化曲线Fig.1 The Current Change Curve of D-Axis When the Controller and the Motor Resistance Are Mismatched and Matched

图2 控制器与电机电阻失配和匹配时q轴电流变化曲线Fig.2 The Current Change Curve of Q-Axis When the Controller and the Motor Resistance Are Mismatched and Matched

图3 控制器与电机电感失配和匹配时d轴电流变化曲线Fig.3 The Current Change Curve of D-Axis When the Controller and the Motor Inductance Are Mismatched and Matched

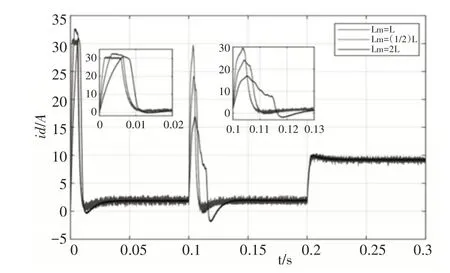
图4 控制器与电机电感失配和匹配时q轴电流变化曲线Fig.4 The Current Change Curve of Q-Axis When the Controller and the Motor Inductance are Mismatched and Matched

图5 控制器与电机磁链失配和匹配时d轴电流变化曲线Fig.5 The Current Change Curve of D-Axis When the Controller and the Motor Flux Are Mismatched and Matched

图6 控制器与电机磁链失配和匹配时q轴电流变化曲线Fig.6 The Current Change Curve of Q-Axis When the Controller and the Motor Flux are Mismatched and Matched

由图1～图6电阻，电感，磁链变化引起的d-q轴电流变化可以看出：定子电阻值增大时，d-q轴电流的峰值降低，但震荡加剧及动态调节时间变长；d-q轴电感值增大时，d-q轴电流的震荡加剧及动态调节时间变长，但d轴电流的峰值增大，而q轴的电流峰值降低；转子磁链降低时，d-q轴电流的峰值降低，动态调节时间变短，但稳态值波动较大，由于q轴电流与转子磁链有关，所以转子磁链变化时q轴电流的稳态误差较大。

因此得出结论：当永磁同步电机与控制器参数失配时，控制性能下降，无法满足精确控制的要求。因此为了提高控制系统性能选择不需要电机电磁参数参与的无模型自适应预测算法设计电机矢量控制系统的内外环控制器，因此不会有参数失配现象的发生，可以从根源上解决参数失配问题。

3 基于高阶滑模补偿的无模型自适应预测控制理论

3.1 离散时间非线性系统动态线性化

任意一个非线性的单输入单输出（SISO）系统可以描述为：

式中：y(k)、u(k)—系统k时刻的输出和输入。

式中系统在k时刻的输入变化量Δu(k)是有界的，即满足|Δu(k)| ≤Ω，其中，Δu(k)=u(k)-u(k-1)。当Δu(k) ≠0时，存在一个PPD时变有界参数φ(k) ∈R，使得式（1）系统可以转换为CFDL模型，即：

并且φ(k)对任意时刻k有界。

3.2 预测模型

（1）式所描述系统用系统增量模型（2）表示的一步向前预测方程为：

则N步向前预测方程为：

3.2.1 高阶滑模补偿器校正

通常预测值与实际输出值由于实际控制中外界干扰的影响存在偏差，因此，为避免累积偏差导致的控制失调，在当前时刻进行预测控制，而在下一时刻则通过误差实时校正预测模型。实际输出值与预测输出值的误差为：

选择滑模面s(k)=e(k)=0，设计新型高阶滑模补偿器如下：

要使≤0，并使式（7）稳定的参数条件如下（M为正常数，其他参数的具体取值第五节给出）：

高阶滑模补偿器具有较高的鲁棒性，而且可以抑制因切换函数带来的高频抖振。校正后的预测输出为：

3.2.2 滚动优化

MFAPC通过滚动优化得到优化性能指标。取二次目标函数：

式中：λ＞0 权重因子；Y*N(k+1)=[y*(k+1)，…，y*(k+N)]T，y*(k+i)—系统在k+i时刻的期望输出。

因此，当前时刻的控制输入：

式中：g=[1，0，…，0]T。

3.2.3 PPD估计算法

上一小节式（4）中A(k)包含PPD 参数φ(k)、φ(k+1)、…、φ(k+Nu-1)，可采用本节改进的投影算法来计算：

但φ(k+1)、φ(k+2)、…、φ(k+Nu-1)不能直接由k时刻的I∕O 数据计算得到，需根据(1)(2)、…(k)预测得到，预测算法如下。

3.3 系统稳定性证明

下面证明以上控制方法的稳定性及跟踪误差收敛性。

由|φ(k)|≤，可得出|φ(k-1)-φ(k)|≤2，因此上式可化为：

由于0 ＜η≤1且μ＞0则存在常数d，使得：

可以得出(k)及(k+j)是有界的。

跟踪误差的收敛性及系统的稳定性的证明如下：

定义跟踪误差为e(k+1)=y*-y(k+1)，综合式（3）、式（12）、式（13）可得：

两端取绝对值得：

其中，由于AT(k)A(k)是一个半正定矩阵，且λ＞0，因此存在P=AT(k)A(k)+λI，使得P和P-1均为正定矩阵。且P-1=P*∕det(P)，其中矩阵P*的伴随矩阵为：

因为PPD值是有界的，故上式是有界的，因此跟踪误差是收敛的。

系统的输入输出有界稳定性证明如下：

因为P正定，故det(P) ＞0，且det(P)是关于λ的首项系数为1 的Nu阶多项式，pi1为Nu-2 阶多项式，因此存在当λ＞λmin时，使得下式成立：

由式（18）和式（24）可得：

因此limk→∞|e(k+1)|=0，且由于y*(k)有界，因此系统输出y(k)也是有界的。

由式（12）和式（13）可以转化为：

因此系统输入也是有界序列。

4 基于高阶滑模补偿的PMSM无模型自适应预测控制器设计

基于高阶滑模补偿的PMSM 无模型自适应预测控制器结构，如图7所示。

图7 基于高阶滑模补偿的PMSM无模型自适应预测控制器结构图Fig.7 Structure Diagram of PMSM Model-Free Adaptive Predictive Controller Based on High-Order Sliding Mode Compensation

4.1 基于高阶滑模补偿的PMSM无模型自适应预测速度控制器设计

则校正后的预测输出为：

二次目标函数为：

采用改进的投影算法来计算φ1(k)，可得：

4.2 基于高阶滑模补偿的PMSM无模型自适应预测电流控制器设计

同样采用改进的投影算法来计算φ2(k)、φ3(k)，可得：

5 基于高阶滑模补偿的PMSM无模型自适应预测控制系统仿真与分析

采用MATLAB∕Simulink 搭建系统仿真模型，如图8 所示。电机参数，如表1所示。速度环中伪梯度向量的初值(1)=0.4、可调参数ε1=0.1、滑模增益α1=2、β1=5、γ1=5，权重因子λ1=0.0001、μ1=5，步长因子η1=1，电流环中伪梯度向量的初值(1)=(1)=0.2、可调参数ε2=ε3=0.1、滑模算法增益α2=α3=1、β2=β3=2、γ2=γ3=2，权重因子λ2=λ3=0.001、μ2=μ2=4，步长因子η2=η3=1，采样时间T=5e-5。PI控制器的参数：kωP=0.11、kωI=5，kidP=kiqP=L*2000、kidI=kiqI=R*2000。

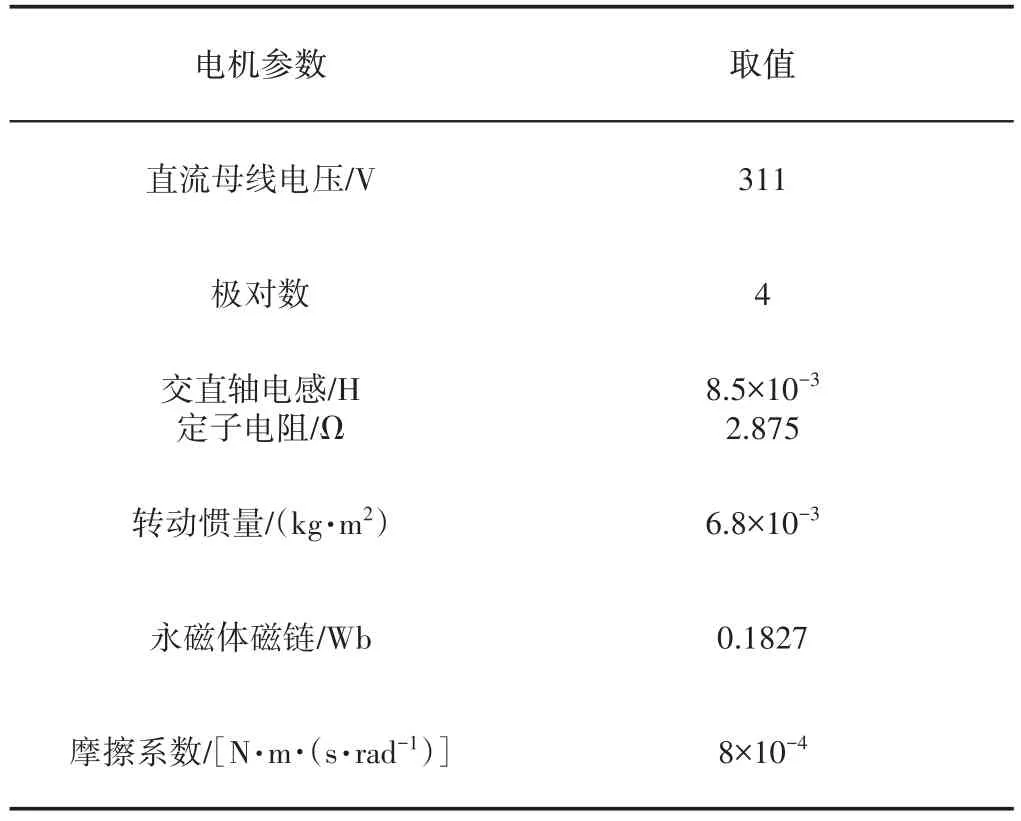
表1 永磁同步电机参数Tab.1 Permanent Magnet Synchronous Motor Parameters

图8 基于高阶滑模补偿的PMSM无模型自适应预测控制系统仿真模型Fig.8 Simulation Model of PMSM Model-Free Adaptive Predictive Control System Based on High-Order Sliding Mode Compensation

仿真中PWM开关频率为10kHz。

（1）基于高阶滑模补偿的PMSM 无模型预测控制变速变载仿真。给定初始转速是600r∕min，负载转矩为2N·m，0.1s转速变为1000r∕min，0.2s 负载转矩变为10N·m。基于高阶滑模补偿的PMSM无模型自适应预测控制系统的电机转速、转矩和d-q轴电流的变化曲线，如图9～图12所示。

图9 电机转速的变化曲线Fig.9 Change Curve of Motor Speed

图10 电机转矩的变化曲线Fig.10 Change Curve of Motor Torque

由图9可得PMSM在带载的状态下起动，PI双闭环控制系统的调节时间0.05s，其超调为21%，MFAPC 双闭环控制系统的调节时间为0.04s，超调为4.5%，而基于高阶滑模补偿的MFAPC双闭环控制系统的调节时间为0.03s，超调为2.0%。

当电机转速增加为1000r∕min时，PI双闭环控制系统的调节时间0.04s，其超调为11%，MFAPC 双闭环控制系统的调节时间为0.035s，超调为2.5%，而基于高阶滑模补偿的MFAPC双闭环控制系统的调节时间为0.02s，超调为1%。

当电机负载转矩增加为10N·m时，PI双闭环控制系统的调节时间0.05s，其超调为9%，MFAPC双闭环控制系统的调节时间为0.03s，超调为2.2%，而基于高阶滑模补偿的MFAPC双闭环控制系统的调节时间为0.015s，超调为1.2%。

由图11～图12可得PMSM在带载的状态下起动，变速，变载时PI双闭环控制系统的d-q轴电流震荡和调节时间比MFAPC双闭环控制系统的大，而基于高阶滑模补偿的MFAPC双闭环控制系统的调节时间更小。

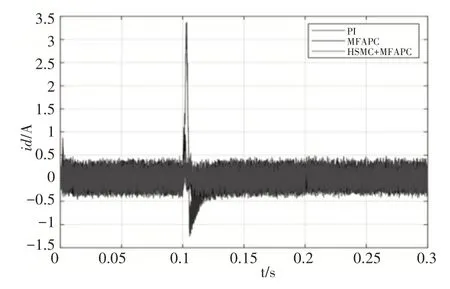
图11 d轴电流的变化曲线Fig.11 Change Curve of d-Axis Current

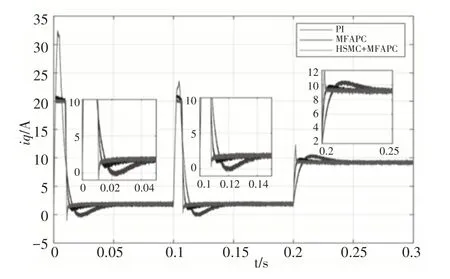
图12 q轴电流的变化曲线Fig.12 Change Curve of q-Axis Current

（2）当电机参数变化时，基于高阶滑模补偿的PMSM无模型预测控制仿真验证。为了验证无模型控制方法是否受电机参数变化的影响，将电机电阻、电感、磁链分别增大和减小，得到d-q轴电流变化仿真图，如图13～图18所示。

图13 电机电阻变化时d轴电流变化曲线Fig.13 The Current Change Curve of d-Axis When the Motor Resistance Changes

图14 电机电阻变化时q轴电流变化曲线Fig.14 The Current Change Curve of q-Axis When the Motor Resistance Changes

图15 电机电感变化时d轴电流变化曲线Fig.15 The Current Change Curve of d-Axis When the Motor Inductance Changes

图16 电机电感变化时q轴电流变化曲线Fig.16 The Current Change Curve of q-Axis When the Motor Inductance Changes

图17 电机磁链变化时d轴电流变化曲线Fig.17 The Current Change Curve of d-Axis When the Motor Flux Changes

图18 电机磁链变化时q轴电流变化曲线Fig.18 The Current Change Curve of q-Axis When the Motor Flux Changes

由图13～图18电阻、电感、磁链变化时得到的d-q轴电流变化曲线可以看出，当电机参数变化时，三条曲线几乎重合，说明基于高阶滑模补偿的PMSM无模型预测控制不受电机运行过程中参数变化的影响。

6 结论

针对在永磁同步电机矢量控制系统中应用模型预测控制方法设计控制器时，其依赖于电机数学模型使得在电机运行过程控制系统易产生参数失配现象，导致控制性能的下降，提出将无模型自适应预测控制方法运用到PMSM中，有效解决电机模型限制和参数失配问题，又由于无模型自适应预测控制方法没有反馈校正环节，易受外部扰动的影响，所以设计高阶滑模补偿器作为校正部分。

从仿真结果可以看出，无模型自适应预测控制的性能高于PI控制，而基于高阶滑模补偿的PMSM无模型自适应预测控制系统相比前两种算法控制性能更高，优势明显。它误差小，动态响应性能，控制精度和鲁棒性高。

并且在电机参数发生变化时，基于高阶滑模补偿的永磁同步电机无模型预测控制系统几乎不受电机参数变化的影响，实用性较强。