面向齿廓变位的圆柱直齿轮啮合动态特性研究
2024-04-27王万明
冯 超,王万明
(1.新乡职业技术学院数控技术学院,河南 新乡 453000;2.郑州大学机械与动力工程学院,河南 郑州 450001)
1 引言
变位直齿轮具有耐久性长、运行平稳、噪音低、振动小等优点,通过有效优化变位系数,变位直齿圆柱齿轮的性能可等效斜齿圆柱齿轮,且可显著降低机械系统的制造和维护成本。研究齿轮系统的内部激励和动态特性是对于提升变位齿轮系统的传动性能具有重要作用[1-2]。
时变啮合刚度(TVMS)是引起齿轮振动和噪声的主要内部激励源之一传输系统[3]。文献[4]提出了一种计算齿轮啮合刚度的解析有限元法,既考虑了复杂地基刚度的有限元计算精度,又考虑了齿轮齿面分析方法的计算速度。文献[5]针对直齿锥齿轮的啮合刚度,提出了将当量齿轮简化为悬臂梁的方法,通过能量法分析了单齿的啮合刚度,该方法的有效性通过有限元方法进行了验证。文献[6]针对齿轮啮合接触性的变化情况,建立了斜齿轮时变啮合刚度模型,分析了不同齿宽和扭矩作用下的齿轮传动系统振动规律。文献[7]分析了裂纹齿轮的齿面接触应力分布情况,在此基础上研究了齿根裂纹深度对直齿轮啮合刚度的影响规律。文献[8]基于Hertz理论研究了不同设计齿形参数对RV 减速器摆线针轮齿的啮合刚度的影响,并采用了有限元分析方法验证了理论模型的合理性。文献[9]基于势能法建立了齿廓修形参数对人字齿轮啮合刚度模型,分析了不同退刀槽宽度以及修形参数对啮合刚度的影响规律,该模型的有效性通过有限元仿真模型得到了验证。文献[10]针对直齿圆柱齿轮啮合刚度的计算,提出了能量法的计算思路,实现了齿轮啮合刚度的快速计算,该方法和有限元方法进行了对比,表明该方法是有效的。
上述研究主要集中在TVMS算法和齿轮传动的动态特性方面,然而在变位直齿圆柱齿轮的几何特性和动力学特性是不同的。基于此,本研究建立了变位直齿圆柱齿轮传动分析模型,研究了齿廓变位对时变啮合刚度(TVMS)和动态特性的影响。
本研究的贡献可以总结为:(1)提出并生成了一种新的变位直齿轮TVMS解析模型;(2)研究了直齿圆柱齿轮各齿廓变位对TVMS动态特性的影响;(3)探讨了直齿轮复合变位对TVMS的影响及其动态特性。
2 时变啮合刚度分析模型
时变啮合刚度(TVMS)是齿轮传动系统中比较典型的周期性激励源,直接影响传动系统的运行性能和寿命。设计参数直接影响时变啮合刚度激振源的程度和强度。因此,建立有效的时变啮合刚度模型对准确预测直齿轮传动系统的动态性能至关重要。
2.1 基于势能法的刚度计算
本研究基于势能法原理[11],将齿轮齿简化为变截面悬臂梁,总势能由Hertzian接触能、弯曲能、剪切能、轴向压缩能和圆角基础能量组成。根据弹性力学,这五种势能可以写成:
式中:F—啮合齿副接触面上齿轮啮合的合力。
单齿轮存储的总势能可以用上述分量刚度描述为:
式中:k—啮合时的总啮合刚度,下标1和2分别为驱动齿轮和从动齿轮。因此,啮合齿轮副的总TVMS可以表述为:
式中:下标i表示第i个啮合齿轮齿。考虑到齿数、模量、齿尖间隙系数等不同的设计参数,可以根据以下两种情况确定齿高:
(1)根圆小于基圆;(2)根圆大于基圆。齿高可以计算为:
式中:下标i—小齿轮和齿轮;
—齿顶系数;
pi—变位系数;
Δq—齿顶变位系数,可表示为Δq=pp+pg-q,其中,q—中心距变位系数。
2.1.1 情况1
如果根圆小于基圆,轮齿的几何形状,如图1所示。齿廓从齿顶圆开始,在齿根圆结束,齿廓是齿顶圆和基圆之间的渐开线曲线,其余的是过渡曲线。根据轮齿几何形状,用于分析刚度组件的几何参数可以表示为:

图1 变位直齿轮的轮齿几何形状(情况1)Fig.1 Tooth Geometry of Modified Spur Gear(case 1)
其中,φ3=arcsin(h1∕Rf),ax=d1∕(φ3-φ2),bx=d1φ3(φ3-φ2)
基圆与根圆过渡曲线的几何关系,如图2所示。

图2 过渡曲线的几何关系(情况1)Fig.2 Geometric Relationship of Transition Curve(case 1)
过渡曲线可以描述为参数h1的函数,参数h1可表示为:
可知,F(h1)是参数h1的非线性复杂函数,在给定F(h1)的情况下,本研究采用Newton-Raphson迭代算法进行方程的求解。
由渐开线和过渡曲线组成的轴向压缩、弯曲和剪切啮合刚度可表述为:
赫兹接触刚度可表述为:
式中:L、E、ν—齿宽、杨氏模量、泊松比。圆角基础刚度可表述为:
其中,β、uf、Sf、L*、M*、P*、Q*可参考文献[12]中的表述。
2.1.2 情况2
如果根圆大于基圆,轮齿的几何形状,如图3所示。齿廓从齿顶圆开始到根圆,其中齿廓是齿顶圆和根圆之间的渐开线曲线。

图3 变位直齿轮的轮齿几何形状(情况2)Fig.3 Tooth Geometry of Modified Spur Gear(case 2)
同理,由渐开线曲线组成的弯曲、剪切和轴向压缩啮合刚度可计算为:
其中,φ4和φ5可通过求解以下耦合方程确定:
2.2 几何关系分析
对于变位系数相等的变位齿轮和小齿轮组,节圆和基圆是不变的。各自的几何关系类似于等效标准直齿轮和小齿轮组的几何关系。然而由于这些圆的不协调变化,变位系数不等的变位齿轮的几何关系需要重新考虑。
特别是在齿轮啮合中,齿轮的节圆不再与参考圆重合,因此纯滚动的位置发生变化,与标准直齿轮的位置不同。基于变位直齿轮的基本理论[13],齿轮啮合开始时的几何关系,如图4所示。

图4 变位直齿轮和小齿轮的几何关系Fig.4 Geometric Relationship Between Modified Spur Gear and Pinion
在齿轮∕小齿轮啮合开始时,作用线和齿轮齿顶圆之间的Ap点发生接触。随着齿轮传动的进行,齿轮和小齿轮最终在作用线和小齿轮齿顶圆的交点处分离。从而小齿轮和齿轮的角度φ1可以写为:
式中:ig—传动比;上标0—角度的初值;下标p、g—小齿轮和齿轮。小齿轮和齿轮的角φ2可表述为:
其中:Np、Ng—小齿轮和齿轮的齿数;sp、sg—小齿轮和齿轮的齿厚;ep、eg—小齿轮和齿轮的节数和齿厚的差值;φ0—参考压力角;inv—渐开线函数。角度初值的数学表达式为:
式中:Rb,i—基圆半径;Ra,g—齿轮上齿顶圆半径;a'—变位后的中心距。
3 变位直齿轮的研究框架
本节根据前述建立的TVMS模型来检验变位直齿圆柱齿轮,研究框架,如图5所述。基于变位直齿圆柱齿轮的振动模态,利用集中质量模型提取其振动响应和统计特征。

图5 基于TVMS模型的变位直齿轮研究框架Fig.5 Research Framework of Modified Spur Gear Based on Tvms Model
齿轮和小齿轮系统的六自由度动力学模型,如图6所示。对于直齿轮,由于啮合刚度影响齿轮副平面而非轴向振动,因此只考虑沿作用线、垂直于作用线的运动和旋转。轴端与轴承相连,采用并联弹簧阻尼装置,动力系统的控制方程可以写成[14]:
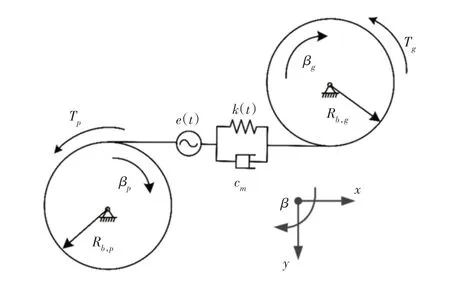
图6 齿轮和小齿轮动力学模型Fig.6 Dynamic Model of Gear and Pinion
式中:mp,g、Ip,g—小齿轮和齿轮的质量和转动惯量;cb、kb—轴承的阻尼和刚度;Tp、Tg—驱动扭矩和负载扭矩;Fm、Ff—啮合力和摩擦力,可以表述为:
式中:e(t)—静态传输误差;μ—摩擦系数。此外,采用等效质量、阻尼比和平均啮合刚度计算啮合阻尼系数cm,可表述为:
式中:ζ—阻尼比;—平均啮合刚度;m—等效质量,可用m=mpmg∕(mp+mg)来描述。因此,由于其他参数是固定的,阻尼比决定了啮合阻尼系数。
为了分析阻尼比对动力分析灵敏度的影响,分别选取ζ为0.07、0.08、0.09和0.1进行仿真分析。从而齿轮系统的动态传输误差(DTE)可以表述为成DTE=xp-xg+Rb,pβp+Rb,gβg-e(t)。啮合齿轮和小齿轮组的设计参数值,如表1所示。
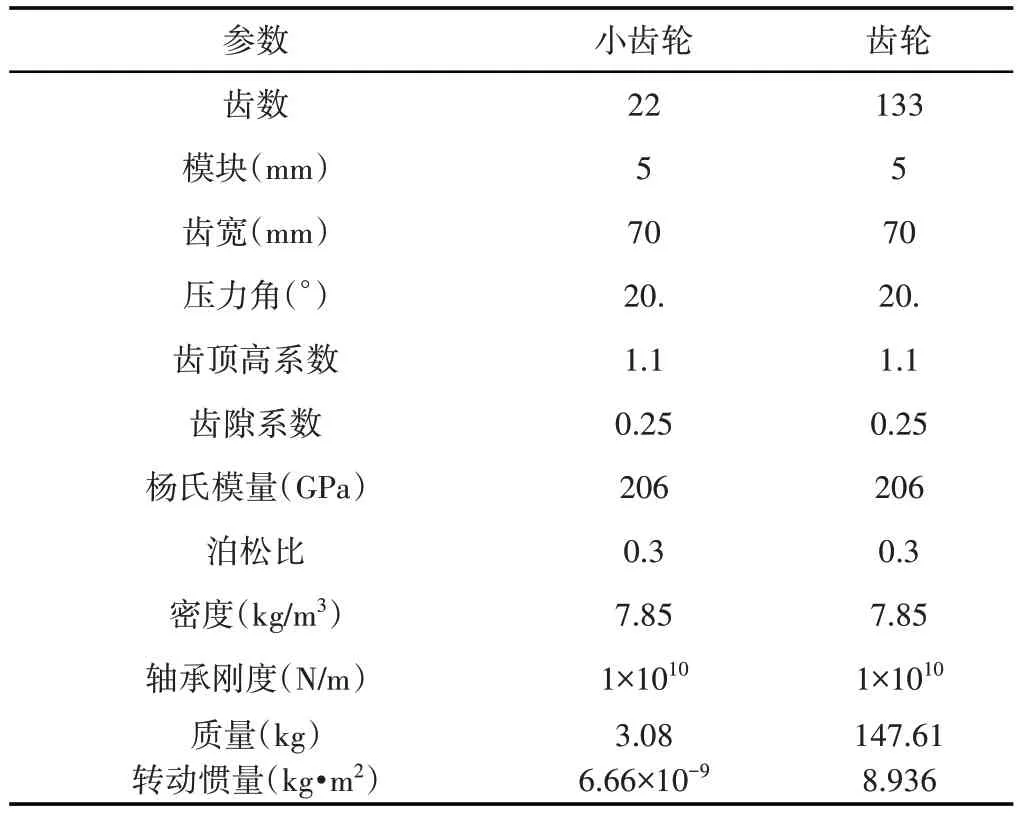
表1 变位直齿轮和小齿轮参数值Tab.1 Parameter Values of Modified Spur Gears and Pinions
为了研究齿廓变位的影响,对不同变位系数的齿轮系统进行了动态仿真[15]。齿轮传动特性反映了齿轮系统相互作用的主要特性,对啮合力和振动加速度有显著影响。本研究利用频谱和统计指标对设计参数进行分析。为了系统地评价齿廓变位对齿轮系统振动的影响,选择了四个时域指标来描述振动加速度的变化趋势,即均方根(RMS)、幅值平方根(SRA)、峰峰值(PPV)、峰度值(KV),这些指标可表述为:
4 案例研究
利用前述提出的TVMS模型和分析框架,本节对单齿变位和复合变位对直齿圆柱齿轮TVMS动态特性的影响。
4.1 单齿变位分析
4.4.1 正变位分析
在研究变位直齿圆柱齿轮的TVMS和动态特性之前,需要了解变位系数对单个齿轮轮齿刚度的影响。本研究选择小齿轮作为研究对象,研究正变位的影响。在此,我们研究了六个变位系数分别为0、0.1、0.2、0.3、0.4和0.5的小齿轮轮齿刚度。不同变位系数下的小齿轮轮齿刚度,如图7所示。总的来说,正变位系数使轮齿更能抵抗高刚度造成的变形。但在啮合开始和啮合结束时,变位系数对刚度的影响是不同的。为了更明显地描述这种影响,提出一个相对于标准直齿圆柱齿轮的比例指标:

图7 不同变位系数下的小齿轮齿轮刚度Fig.7 Single Pinion Tooth Stiffness with Different Modification Coefficients
式中:ki—第i个齿廓变位小齿轮的刚度;k0—不移位小齿轮的标准刚度,即pp=0。
不同变位系数下的单齿轮齿刚度比例,如图8所示。可以看出正变位系数越大,啮合过程中刚度曲线越陡。正变位系数越大,啮合初期的刚度越高,啮合结束阶段的刚度越低。
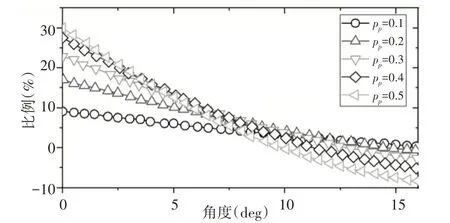
图8 单廓轮齿刚度比例的比较Fig.8 Comparison of Stiffness Ratio of Single Profile Gear Teeth
为了深入分析各参数对齿轮系统的影响,进一步分析基于正变位系数的TVMS。根据上述分析模型得出的TVMS结果,如图9所示。为了更清晰地描述齿轮啮合刚度和接触比变位系数的影响,选择从(0~25)°的旋转角小齿轮。从综合啮合刚度来看,TVMS随变位系数的增大而减小。随着变位系数的增大,TVMS的变化率也逐渐增大。这说明正变位是一种非常敏感的设计,在选择所需参数值时需要进行灵敏度分析。
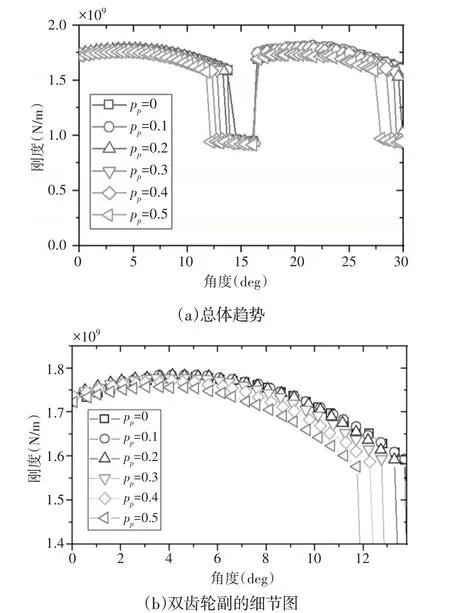
图9 不同变位系数的TVMS比较Fig.9 Comparison of TVMS with Different Modification Coefficients
正变位时TVMS的均值变化和标准差,如图10所示。均值和标准差分别可以描述TVMS的平均水平和振荡程度,这两个指标的变化与变位系数分别呈现出非线性关系。平均值随着轻微的正变位而缓慢下降,而随着大的正变位而加速下降。同时,标准差随着轻微的正变位而急剧增加,而随着较大的正变位而减缓增长。为了定量分析正变位的影响,分别提取不同阻尼比下变位系数为0、0.1、0.2、0.3、0.4和0.5的统计指标。与标准直齿轮的比例比较,如图11所示。可以看出随着变位系数的增加,除阻尼比为0.07时PPV外,其他指标均呈单调增长趋势。这表明正变位会加重齿轮副的振动,而KV在变位系数较小的范围内为负值。结果表明,轻微的变位系数会降低峰值,而较大的变位系数会增加峰值,且可以发现啮合阻尼系数对统计指标不敏感。
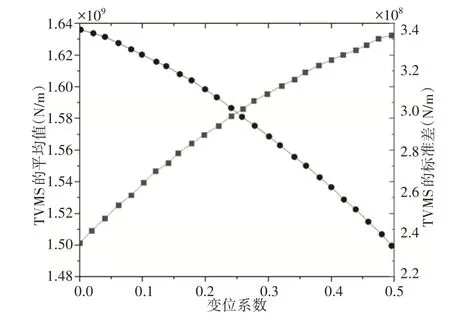
图10 正变位的TVMS的平均值和标准差Fig.10 Mean Value and Standard Deviation of TVMS for the Positive Shifts

图11 DTE正变位的统计指标Fig.11 Statistical Indicators of DTE for the Positive Shifts
4.4.2 负变位分析
为平衡齿轮和小齿轮副的疲劳寿命,工程上一般采用负变位的齿轮,以达到相同的寿命设计。本研究选择六个变位系数值分别为0,-0.1,-0.2,-0.3,-0.4和-0.5。不同变位系数值下的齿轮单齿刚度,如图12所示。

图12 单齿轮的齿刚度对齿轮具有不同的变位系数值Fig.12 Single Gear Tooth Stiffness on Gear with Different Modification Coefficient Values
变位变位系数使齿轮比标准直齿圆柱齿轮更柔软。与正变位一样,变位系数在啮合的开始阶段和结束阶段对刚度的影响是不同的。啮合开始时,刚度损失较小,随着啮合的进行,刚度损失逐渐增大。不同变位系数值下的单齿轮齿刚度变化率,如图13所示。与正变位不同,代表啮合刚度变化的曲线均在各自的抛物线曲线中,且不存在交叉。可以发现最大的刚度损失出现在啮合的中间位置。随着变位系数的减小(实数值),变化率变得更弯曲。
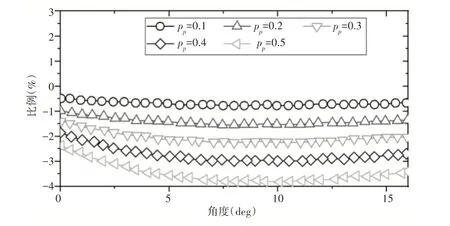
图13 单齿轮齿刚度的变化率Fig.13 Rate of Change of Single Gear Tooth Stiffness
为了深入分析各参数对齿轮系统的影响,根据上述分析模型得出的TVMS结果,如图14所示。为了更清晰地描述齿轮啮合刚度和接触比变位系数的影响,仍然选择旋转角度范围为(0~25)°小齿轮。基于负变位设计的直齿轮在啮合初始阶段的TVMS小于标准齿轮,随着啮合的进行,综合啮合刚度逐渐增大。最终变位系数较小的TVMS会超过变位系数较大的TVMS。且可以看出变位系数较小的TVM具有较高的接触比,因此负变位可以改善传动的平稳性和连续性。

图14 不同变位系数的TVMS比较Fig.14 Comparison of TVMS with Different Modification Coefficients
负变位时TVMS的平均值和标准差,如图15所示。这两个指标的变化与变位系数呈近似线性关系。随着变位系数的减小(实数值),平均值逐渐增加,而标准差则有规律地下降。
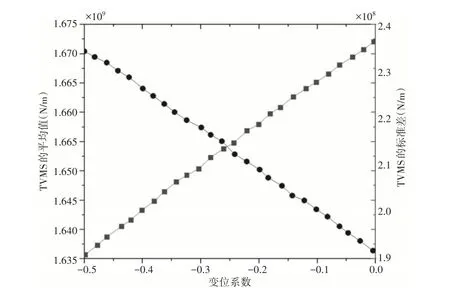
图15 负变位的TVMS的平均值和标准差Fig.15 Mean Value and Standard Deviation of TVMS for the Negative Shifts
为了定量分析负变位的影响,提取了DTE的统计指标,在不同阻尼比下,变位系数取0、-0.1、-0.2、-0.3、-0.4和-0.5。与标准直齿轮成比例的比较,如图16所示。结果表明随着变位系数的减小,各项指标均呈现单调变化。RMS和RSA呈现下降趋势,表明负变位可以抑制齿轮副的振动。此外,KV改善缓慢,但PPV变化不明显。
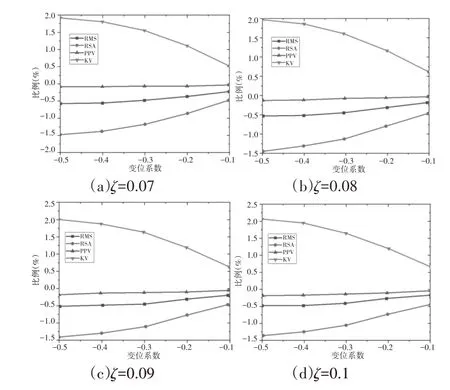
图16 DTE正变位的统计指标Fig.16 Statistical Indicators of DTE for the Negative Shifts
4.2 复合变位分析
在现实中,一般使用齿形变换来设计齿轮和小齿轮副的机械性能。s0齿轮传动和S齿轮传动是变位直齿圆柱齿轮复合修形的两种形式[16]。前者的总变位系数为0,后者的总变位系数非0。
不同复合变位设计的TVMS曲线,如图17所示。第一组和第二组是具有正总变位系数的S齿轮,第三组和第四组是具有负总变位系数的S齿轮,第五组是s0齿轮,第六组标准直齿轮。第一组中pp=0.4,pg=0.1,命名为组1;第二组中pp=0.2,pg=0.1,命名为组2;第三组中pp=0.1,pg=-0.6,命名为组3;第四组中pp=0.1,pg=-0.4,命名为组4;第五组中pp=0.1,pg=-0.1,命名为组5;第六组中pp=0,pg=0,命名为组6。从图中可以看出,负总变位系数增加了接触比和啮合刚度,而正总变位系数可以显著降低接触比和啮合刚度,可以看出s0齿轮对TVMS的影响相对较小。

图17 不同复合变位的TVMS的比较Fig.17 Comparisons of TVMS with Different Compound Shifts
不同复合变位下TVMS的均值和标准差,如图18所示。总变位系数为负时,TVMS的均值较高,而标准差则呈现相反的变化趋势。不同总变位系数对平均值的影响在小齿轮变位系数处更分散,在大齿轮变位系数处更接近。
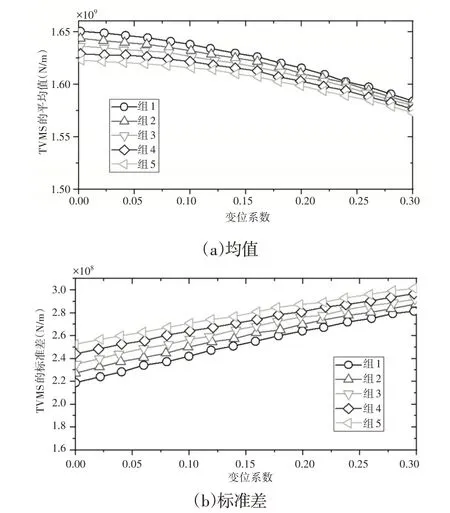
图18 复合变位的TVMS的平均值和标准差Fig.18 Mean Value and Standard Deviation of TVMS for the Compound Shifts
不同阻尼比下复合变位DTE统计指标的变化情况,如图19所示。

图19 复合变位的DTE统计指标Fig.19 Statistical Indicators of DTE for the Compound Shifts
与频谱相似,正复合变位的指标高于负复合变位的指标,RSA差甚至达到了15%左右。而KV曲线呈现折线,说明S齿轮传动使齿轮系统的时域波形变得更陡。s0齿轮的统计指标与标准直齿轮存在一定的差异,这主要是由于变位系数在数值上相等,但符号相反,导致小齿轮和齿轮变位是不同的。
5 结论
本研究建立了变位直齿圆柱齿轮传动分析模型,探讨了齿廓变位直齿轮对齿轮系统运行性能的影响。该模型可以直接得到以小齿轮转角为自变量的直齿圆柱齿轮系统动态特性的函数,考虑了两种不同的齿廓变位几何设计。
根据所建立的分析模型,在所给定的评估方法下采用数值模拟方法研究了轮廓偏移对TVMS和动态特性的影响,结果表明单个齿廓的正变位会降低轮齿的刚度和TVMS,单个齿廓的负变位可以提高轮齿的刚度和TVMS。对于复合变位,采用正复合变位的S齿轮传动可以降低TVMS,但加剧了齿轮系统的振动,采用负复合变位的S齿轮传动会导致TVMS 升高,并显著降低振动,s0齿轮变位对时变啮合刚度(TVMS)影响较小,但对动态特性影响较大。
