基于多视图几何的无人机单目视觉定位初始化*
2024-04-27鹿珂珂王雅平吴俊峰
鹿珂珂,王雅平,王 超,吴俊峰
(海军航空大学,山东 烟台 264001)
0 引言
近几年发展最快的新科技,当属无人机的强势崛起,军用无人机在监视与侦察、特定目标追踪、战斗毁伤评估、火力支援等作战任务中发挥了越来越重要的作用[1]。在民用领域,无人机也正展现出越来越丰富的可能性,航拍、植保,替代电力工人巡线等。为了达到稳定、鲁棒的飞行效果,无人机通常需要一种精确且实时的位姿状态估计方法。最常用的导航方式为卫星导航,但是只能进行大范围粗略地估计,同时卫星信号易受干扰和欺骗。此外,在室内等卫星导航信号失效的场景下,无人机无法实时定位,仅使用单目相机的方法,由于其体积小、成本低和硬件设置简单,而获得了社会的极大关注[2-6]。当利用单目视觉为无人机进行定位时,需要进行初始化,通过初始化求解得到位姿,然后作为后端优化的初始值,能够有效地使后端的非线性优化收敛,这在实际中得到了有效的验证[7-10]。而视觉里程计的实现通常有3 种方法[11-12]:使用两组二维像素坐标使用三角约束求解;利用三维点和它们在相机的投影位置时,利用多点透视成像(perspective-n-point,PnP)求解;利用两组三维点时,使用光束平差法求解。然而,上述方法不同程度存在耗时较长和位姿估计不准确的问题。因此,在上述研究基础上,提出基于多视图几何中的基本原理,组合利用滑窗方法、三角约束、PnP 和光束平差法,快速准确地实现无人机位姿估计初始化的方法,并通过数据集验证了纯视觉初始化效果。实验结果显示,本文提出的方法在运动充分的情况下,仅需2~3 s时间,即可在15帧的活动窗口内实现快速准确的位姿估计初始化,在EuRoC MAV 数据集[13]的实验结果表明,本文提出的算法在初始化时间和精度上都优于ORB-SLAM3[14]和S-MSCKF[15]算法,位姿精度在对齐后,可以有效加快后端非线性优化的收敛速度。基于该初始化算法的视觉里程计,取得了较为理想的实验效果。
1 基于多视图几何的初始化算法流程
基于多视图几何的定位初始化算法流程组合运用了滑窗方法、三角约束、PnP 和光束平差法,具体流程如图1所示。基于在利用单目视觉进行无人机位姿估计过程中,随着捕获视觉帧的增多,路标点也会增多,全局优化的计算效率会不断下降,因此,算法首先使用滑动窗口方法进行数据预处理,将优化计算的视觉帧限制在一定的数量。由于无人机载处理器性能有限,处理所有图像帧时,实时性较差,而且无人机悬停时,会产生大量信息冗余的图像帧,从而导致很多无用的优化计算,甚至使优化问题退化,因此,从一系列普通帧中选出关键帧作为局部帧的代表,记录局部信息。初始化算法在视觉前端得到的图像帧已经填满滑动窗口时启动,并且通过无人机载IMU 进行判断,保证有充分的运动激励。由于纯视觉无法得知世界坐标系的信息,算法通过检查当前帧和滑动窗口中的所有帧对应的特征点,找到具有稳定跟踪特征点和足够视差的参考帧,利用对极约束求得当前帧相对参考帧的位姿。随后,利用特征点在参考帧和当前帧上的坐标,以及相对位姿矩阵,三角化得到特征点在空间中的位置,即特征点的深度。在已知多个特征点坐标和这些点的像素坐标情况下,使用PnP 求解当前帧和参考帧之间的图像帧位姿,随后使用递推迭代上述过程,求得所有空间点位置和图像帧相对于参考帧的位姿,最后利用BA 算法将空间点位置作为优化变量,进行联合优化,得到初始化窗口中所有图像帧的对应位姿,完成初始化过程。

图1 基于多视图几何的单目视觉定位初始化流程图Fig.1 Flow chart of initialization of monocular visual positioning based on multi-view geometry
2 基于多视图几何的初始化算法实现
2.1 图像预处理
真实世界中的物体在相机坐标系中的坐标位置,投影到拍摄图像上的像素坐标可以使用针孔相机模型,这一映射关系需要使用相机内参。相机透镜的成像过程还会引入畸变,一般需要使用畸变参数进行校正。相机的内参和畸变参数可以使用张正友标定方法得到。
式中,[u,v]T为空间点在成像平面上的像素坐标;PT=[X,Y,Z]T为空间点在相机坐标系中的三维坐标,矩阵K为相机的内参矩阵。
式中,[x,y]T为空间点在归一化平面上的坐标;r为归一化平面上空间点到坐标原点的距离,k1,k2,k3,p1,p2为相机畸变参数。为了方便从图像中提取特征点,可以对图像进行直方图均衡化处理,改变图像的对比度。
2.2 特征点选取与跟踪
对每一新的图像帧使用KLT 稀疏光流算法进行特征跟踪[16],对于匹配成功的特征点,使用随机采样一致性算法(random sample consensus,RANSAC)计算基础矩阵进行误匹配的筛选[17]。误匹配筛选完成后,将特征点进行畸变矫正,并投影到单位球上。同时检测新的特征点,使每一帧图像中具有最小数目的特征点[18]。在检测新的特征点时,通过设置相邻特征之间的最小间隔像素,使特征分布符合正态分布。
选择关键帧考虑两个方面:关键帧特征点数量要充足、特征点分布要尽量均匀;关键帧之间既存在约束,又有尽量少的信息冗余。因此,在当前帧和上一关键帧跟踪特征点的平均视差超出设定的阈值时,就将当前帧设为关键帧,此外,如果当前帧跟踪到的特征点数目低于某一阈值时,为防止特征跟踪的完全丢失,将当前帧设为关键帧。需要注意的是,相机旋转和平移都会产生视差,而相机纯旋转时,特征点将无法被三角化。
从滑动窗口内的第1帧开始计算每一帧和当前帧的匹配特征点,寻找与当前帧共视点数较多、且视差量较大的作为参考帧。在滑动窗口内,记录所有能够被关键帧观测到的特征点,而对于每个特征点,同时记录能够观测到该特征点的图像帧序列,以及特征点在对应图像帧中的相关信息。
2.3 对极约束和三角化
如图2 所示,场景中空间点在不同视角下像点之间的约束关系称为对极约束,基础矩阵则是这种约束关系的代数表示。假设参考帧I与当前帧C具有N对匹配好的特征点,基础矩阵F=K-Tt∧RK-1是3×3的矩阵,而且使用的是齐次坐标系,因此,仅用8 个匹配的特征点即可求解F,这种方法称为8 点法。一般情况下,匹配特征点数N远大于8,可以采用最小二乘法求解基础矩阵F,但这要求特征点的匹配是正确的,而实际情况中,往往存在外点,采用RANSAC算法来解决。
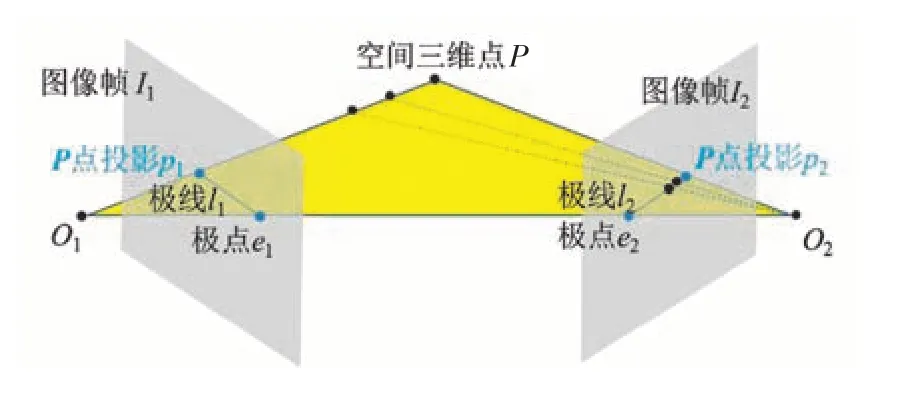
图2 对极约束示意图Fig.2 Schematic diagram of epipolar constraints
2.4 PnP(Perspective-n-Point)
已知M个特征点在参考帧I坐标系中的位置,如图3 所示,找到其中与I+1 帧的N个共视点在I+1帧上的像素坐标,可以采用PnP 算法求取I+1 帧相对I帧的位姿。以此类推,可以得到I帧到当前帧C之间所有帧的位姿估计,以及第1帧到第I-1帧的所有位姿。在此基础上,三角化得到所有共视点的空间位置。
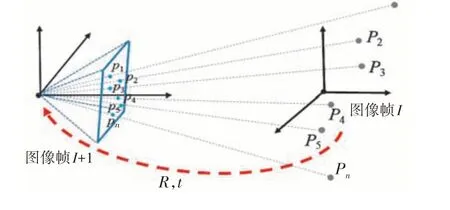
图3 三角化示意图Fig.3 Schematic diagram of triangulation
2.5 BA(bundle adjustment)光束平差法
在使用递推迭代方法求得所有空间点位置和图像帧相对于参考帧的位姿之后,固定住I帧的位置和姿态,固定住最后一帧C的位置。利用BA(bundle adjustment)光束平差法算法,将所有的相机位姿和空间点位置作为优化变量,进行联合优化。
如下页图4所示,令点Pj为位姿Ti的相机拍摄到的图像归一化坐标系上的坐标为,其重投影后的图像归一化坐标系下的坐标为,其中,是为了在计算时能不受相机内参影响,k和k'是将齐次坐标转换为非齐次坐标的常数项,可以得到该重投影误差为:eij=uij-vij。
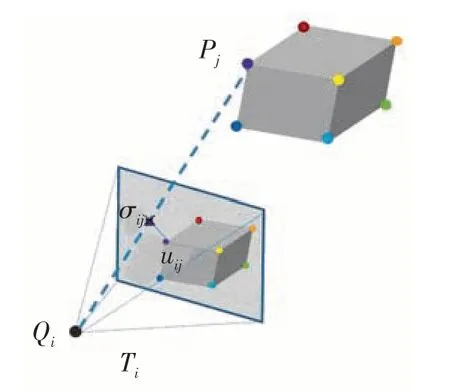
图4 重投影误差示意图Fig.4 Schematic diagram of re-projection errors
BA就是将所有的重投影误差的和最小化:
其中,当点Pj在相机Ti中有投影时σij=1,否则为σij=0。
3 实验分析
在EuRoC MAV数据集上,使用笔记本电脑进行测试,电脑型号为Lenovo Thinkpad E14,拥有Intel酷睿i7 10510U 1.8 GHz,8 G 内存。其中,滑动窗口大小选择为10 帧,对于不同数据集进行测试,关键帧的选择如图5 所示,图中标识的点对应于图像的特征点,不同颜色深度显示了特征点被跟踪的次数。由于使用IMU 对图像关键帧进行了选择,保证了关键帧图像之间具有充分的运动激励,使后续算法可以更为鲁棒。

图5 MH_05数据集上的关键帧选取Fig.5 Key frame selection on the MH_05 dataset
在EuRoC 所有数据集上进行初始化,完成的初始化首帧时间统计表格如表1 所示,表中使用Unix系统时,单位为s,从表中可以看到,本文算法完成初始化时间与ORBSLAM3 相近,在MH01、MH02、MH04、V101 和V202 这5 个数据集上完成初始化得到位姿的图像帧比数据集给出的真值时间还要早。

表1 位姿估计完成初始化首帧时间Table 1 The first frame time when the pose estimation is initialized
可以与真值进行对比的数据集初始化结果误差图如图6 所示,图示轨迹是在对齐定位结果的情况下绘制,可见初始化结果与真值基本一致。误差统计结果如表2所示,其中,同时考虑了旋转和位移得到的相对位姿误差估计结果,单位无量纲,从表中可以看到,本文设计的方法行之有效,能够为后端的非线性优化,获取较为准确的初始值。
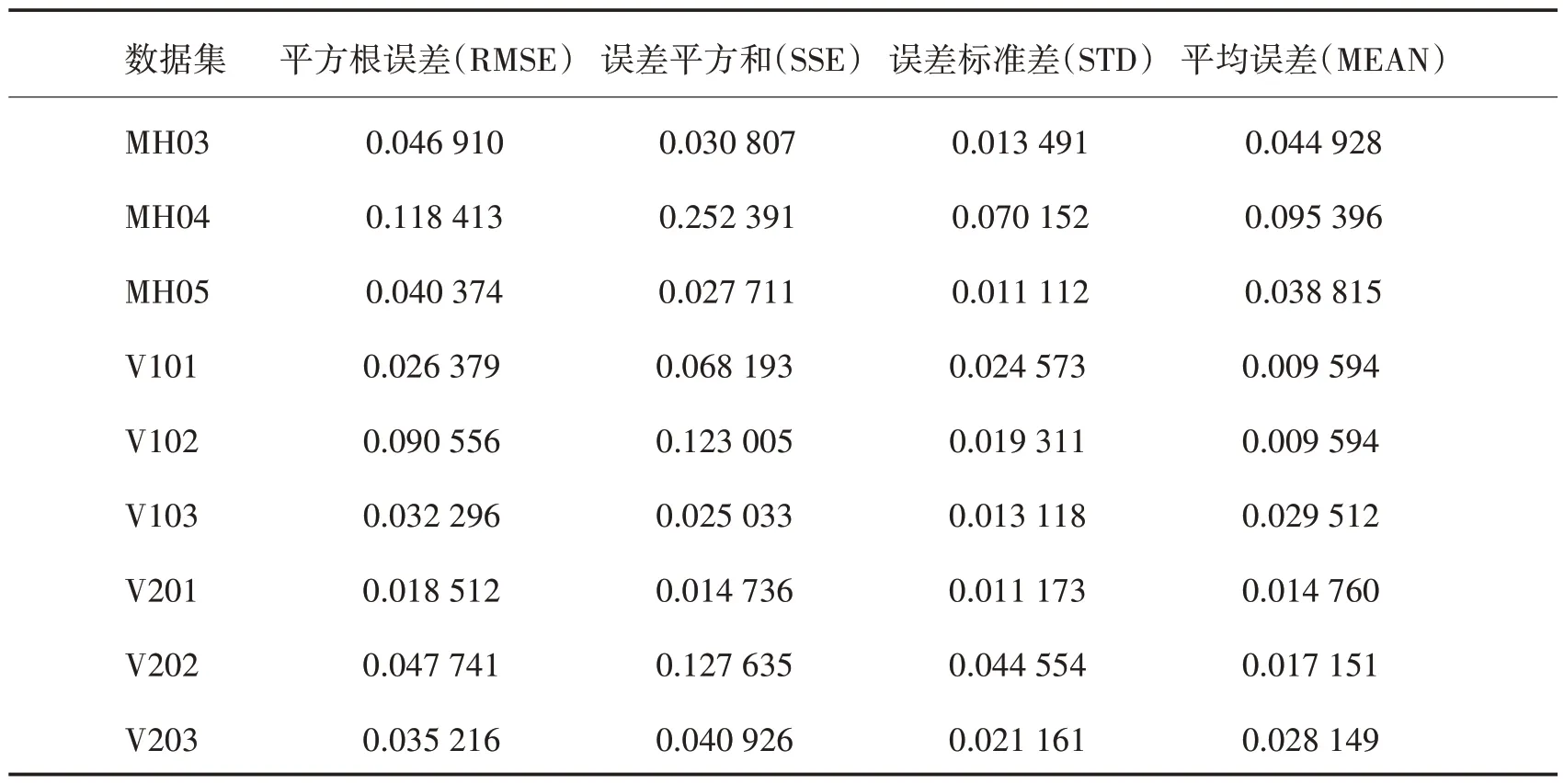
表2 位姿估计初始化误差统计Table 2 Pose estimation initialization error statistics

图6 位姿初始化轨迹误差图Fig.6 Pose initialization trajectory error diagram
作为对比,选取V102数据集,跟ORB和SMSCKF算法进行尺度对齐和修正之后的误差统计结果如表3所示,需要注意的是,对应结果是分别截取了不同算法下对应时间的结果。

表3 不同算法初始化误差对比Table 3 Comparison of initialization errors of different algorithms
绘制V102 数据集下不同算法的轨迹图,如图7和图8 所示,可见本文算法结果相比其他算法精度要更高。从图8 中可见,本文算法在敏感到有充分运动激励时才进行初始化,这样能够保证关键帧之间有足够的视差,因此,得到相对更为准确的初始化结果。

图7 V102数据集初始化定位轨迹图Fig.7 Initialization positioning trajectory diagram of V102 data set

图8 V102数据集三轴轨迹图Fig.8 Three-axis trajectory diagram of V102 dataset
图9 是在数据集基于上述初始化过程,使用纯视觉定位的结果。其中,视觉定位结果未使用回环检测,由于单目视觉轨迹的估计,无法获得尺度真值,因此,对图中的轨迹与真值进行了对齐,可以看出是在本文提出视觉初始化的基础上实现的视觉定位,能够有效跟踪真实轨迹。
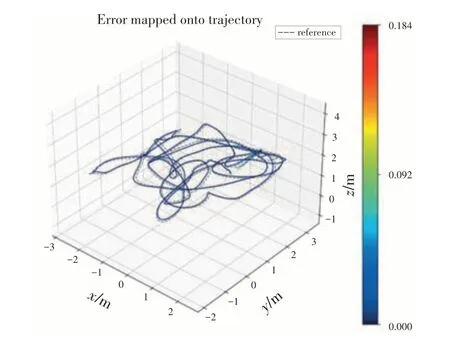
图9 V102数据集视觉定位结果Fig.9 Visual positioning results of 9V102 data set
4 结论
本文提出了一种无人机载视觉定位系统鲁棒的初始化方法,该方法基于多视图几何原理,通过滑动窗口限制实时运算量,综合运用三角化、PnP 和BA 优化,得到所有图像帧相对参考帧的相对位姿,完成单目视觉的初始化,实验结果显示,本文提出的方法快速准确,为快速启动无人机视觉或者视觉惯性组合导航提供初始值。单目视觉定位算法存在尺度的问题,后续实际应用过程中,需要进一步融合IMU 的数据,实现更为完备的初始化结果和定位效果。
