在初中课堂上发展基础数学知识的有效方法

文/中山纪念中学火炬二中 林 建

《义务教育数学课程标准（2022年版）》重申：课程目标的确立要以学生核心素养的培养为出发点，鲜明体现数学教育的育人意义。 在数学课堂中， 我们应该精心打造一个以学生为中心的教育模式， 让学生在实践中发现问题、解决问题，从而提升数学素养和核心竞争力。 《数学教育心理学》指出，数学不仅仅是人类思维的表达形式， 更代表了人们不懈追求完美的意志， 精益求精的推理，以及严谨周详的思维，它为人类提供了通过数学语言去描述宇宙和探索世界的无限可能和机会。初中生学习数学， 就是将数学基本概念、规律、事实和方法逐渐内化为具有内在逻辑联系与排列的认知结构， 这一认识模式是学生对数学新问题认识的核心， 要在数学学习中不断探究和丰富， 下面从三个角度阐述如何构筑认知结构。

一、注重培养数学思维方式教学，构建认知框架，引导会思考的能力

在数学学习的全过程中， 教师需鼓励学生积极参与数学的探究和思维的深化， 并深刻阐述数学思想方法的重要性， 指导学生更好地理解和掌握数学思想方法。 教师应该让学生围绕各种信息和观念展开深入思考和加工转换， 用新知识和旧知识进行整合和概括， 解释所关注的现象，并构建新的假设和推论。这样， 学生便可以形成自己独特的思维方式，最终实现“会用数学的思维思考现实世界”的核心素养。

例1： 讲解分式有意义及分式的值为0 的条件。

例2：在“同底数幂的乘法”教学中，我们可以分以下几步进行：

（1）观察分析：103×102=10×10×10×10×10=10523×22=2×2×2×2×2=25， 知道这是在特殊情况下得到的结论。

（2）同理a3×a2=a×a×a×a×a=a5，这是底数由特殊到一般情况下的结论。

（4）通过这些例子，我们可以得出同底数幂相乘的一般规律： 底数不变，指数相加。这个规律可以应用于任何同底数的幂运算中。

随着难度逐渐增加， 思维方式也随之转变，这反映出了数学思维方式的演变过程。 教师要抓住知识的连接点，以上两道例题在知识衔接处引入设问， 激发学生的探索欲望，从学生原有的认知结构触发新知生长点，进而组织学生对新旧知识进行比较、寻找相同点和不同点，从而剖析新旧知识的分化点，并将新知识完美地融入到原有的认知结构中，推动学生数学认知结构的扩大和发展。

二、让学生动手使用学具，发掘新知，构建认知框架，激发学生的表达技巧

《义务教育数学课程标准（2022年版）》强调通过综合运用数学知识和跨学科的知识多角度去寻求问题、解决问题，进而形成模型观念和数据观念， 提升学生的数学素养和创造力。 教师应该带领学生通过一个个实际问题的研究， 深入了解问题的本质，进而引导学生提出假设、制定并实施研究方案以记录结果，让学生不断积累数学实践经验，逐渐形成 “善于用数学语言表述现实世界”的核心素养。

例3： 采用项目式学习的方式测量树高。

根据光的反射定律， 使用一面镜子和一根皮尺，设计测量方案，具体操作如下：

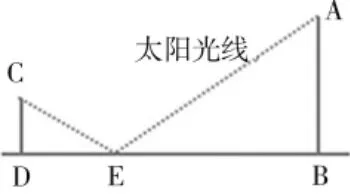
在 E点摆放一面镜子，距离树 （A 点和B 点）八米，随后站在点D 向后退， 直到观察者的视线投射到镜面中，在其中成功捕捉到树梢顶点A。接着， 用一根皮尺测量出观察者所在位置点D 与镜子的距离为三米，而观察者自身高度为两米。 通过这些数据，精准计算出整棵树（AB）的高度。

提供以下测量工具：一根皮尺，一副教学用三角板， 一根长为2.5米的标杆和一架高1.5 米的测角仪。 请你设计一份测量方案， 以测算树高。

类比：测量学校旗杆的高度。

在校园内进行旗杆高度测量时， 学生们可以运用多种方法完成任务。

如借助测倾器， 在不同的位置上测量仰角， 然后运用解直角三角形的技巧来推算旗杆的高度。 如通过比较旗杆的影长与实际高度，按比例关系求解旗杆的高度。

当你看到学生利用所学的知识解决实际问题时，自然会感到欣慰。例如， 有一组学生发现当旗杆绳子落地2 米时，他们拉出绳长6 米，运用勾股定理测出旗杆的高度， 何其简便！

在知识交接的关键时刻， 教师应巧妙提出启发性问题，引发探索，使学生将新知完美融入到原有的认知结构中。通过巧妙的操作学具，让学生手脑同时发力， 让大脑的左右半球同时得到充分开发和利用，激发学习兴趣，提高学习效果，从而更好地掌握新的知识，高效建构知识。

三、鼓励学生独立阅读学习，深入探索未知领域，搭建知识框架，引导学生以观察为先

《义务教育数学课程标准（2022年版）》提出：在教学活动中，学与教是相互交融的， 学生才是真正的主角。教师要引导学生独立思考、亲手实践、积极探究、协力合作等激发学习的热情和主动性， 让学生成为学习的主控人，从而更好地掌握知识，学会学习的方法和技能。

例4： 在学习全等三角形的判定定理一课时，设计如下问题：

已知：AD=BC，∠ABC=∠BAD（如图右）

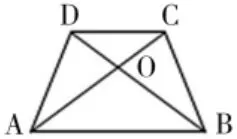
（1）哪两个三角形可以联系起来， 是通过公共边AB 以及∠ABC=∠BAD 这一已知条件来确定的？

（2）求证：ΔABD≌ΔBAC？

（3）证明：OA=OB；

（4）证明：ΔADO≌ΔBCO.

在授课新领域时， 教师应该抓住课程主旨，特别是在难点、重点和新旧知识的衔接处， 以有启迪性的问题来激发学生的好奇心， 让他们自主探究和讨论， 帮助学生逐步养成数学思维模式并观察世界， 培养学生的想象力和创新意识。

总之， 培养初中数学课堂的数学核心素养需要善于调动学生内在的学习积极性。 教师应该运用情境性、支架式和随机通达教学方法，注重数学思维方式的教学， 通过操作数学教具和自主探究来让学生有目的、 有计划、 有组织地学习数学知识，培养数学能力，提高智力水平，同时构建起良好的认知结构， 从而进一步地促进学生基础数学知识的学习。