融合空谱特征的MR?鄄KRVFL高光谱地物识别模型研究

郭国璐 范玉刚 冯晓苏

基金项目：工业控制技术国家重点实验室（浙江大学）开放课题（批准号：ICT2022B06）资助。

作者简介：郭国璐（1994-），硕士研究生，从事图像处理、模式识别的研究。

通讯作者：范玉刚（1973-），副教授，从事系统状态监测、图像处理等方向的研究，931320583@qq.com。

引用本文：郭国璐，范玉刚，冯晓苏.融合空谱特征的MR-KRVFL高光谱地物识别模型研究［J］.化工自动化及仪表，2024，51（2）：284-293.

DOI：10.20030/j.cnki.1000-3932.202402018

摘 要 针对高光谱图像复杂空谱特性影响地物识别模型分类精度的问题，提出一种融合空谱特征的流形正则化核随机向量函数连接网络（MR-KRVFL）高光谱图像地物识别方法。首先，对高光谱图像进行熵率超像素分割（ERS），获取对应的同质区域；其次，利用主元分析（PCA）对同质区域进行降维并提取其空谱联合特征；最后，基于空谱特征信息，构造核随机向量函数连接网络（KRVFL）地物识别模型，并对模型进行流形正则化约束，提高高光谱图像地物识别模型的泛化性能。将该模型应用于Indian Pines和Pavia University高光谱数据集，分类精度达到了96.84%和98.83%，证明所提模型的有效性。

关键词 熵率超像素分割 高光譜图像 核函数 流形正则化 分类精度 地物识别

中图分类号 TP751；P407.8  文献标志码 A   文章编号 1000-3932（2024）02-0284-10

高光谱图像含有数十至上百个窄波段的地物光谱信号，成为土地利用分类相当丰富完备的光谱信息来源，在地质学［1］、精细农业［2］、林业［3］等领域都具有较高的应用价值，近年来，已逐渐成为机器学习和机器视觉领域的研究热点，并取得了大量的研究成果。

在发展之初，学者们只采用光谱信息对高光谱图像进行分类，由于缺乏空间特征的有效利用，分类效果往往不理想。利用高光谱图像所蕴含的空间信息，可进一步强化每个像素点所代表目标的特征辨识度，提高分类识别精度［4］。文献［5］利用超像素提取高光谱图像空谱特征的方法，有效降低了计算量并提高了分类精度；文献［6］将熵率超像素分割（Entropy Rate Hyperpixel Segmentation，ERS）引入自适应字典中，充分利用其空谱信息，解决了高光谱图像小样本情况下分类精度低的问题；文献［7］将主元分析（Principal Component Analysis，PCA）延展到超像素分割领域，提出一种联合空谱信息的特征提取方法，极大地改善了高光谱图像的分类效果。

充分利用所提取到的空谱信息，建立稳定的地物识别模型是实现高光谱图像分类的关键。极限学习机（Extreme Learning Machine，ELM）以其良好的非线性拟合能力和高效的学习效率广泛应用于高光谱图像分类领域，但ELM网络中隐含层参数的随机输出容易导致部分神经元成为无效神经元，为此文献［8］提出了核极限学习机（Kenel Extreme Learning Machine，KELM）用于高光谱图像的分类，通过核函数代替ELM的隐含层，使其输出神经元更为稳定。随机向量函数连接网络（Random Vector Functional Link Network，RVFL）的学习行为类似于ELM，不同的是RVFL采用输入层与输出层直连的方式，有效增强了输入输出数据的关联，但RVFL具有随机参数特征，模型不稳定。文献［9］提出一种值偏差约束的RVFL模型，基于结构风险最小化理论和加权最小二乘法对权重参数进行限制，提高了模型的鲁棒性。

上述模型在训练过程中都忽略了数据样本间的结构信息。因此，笔者通过核随机向量函数连接网络（Kenel Random Vector Functional Link Network，KRVFL）与RVFL的输出层结合，提出融合空谱特征的流形正则化核随机向量函数连接网络（Manifold Multilayer Kenel Random Vector Function Link Network，MR-KRVFL）高光谱地物识别算法，以样本间的局部几何信息构造拉普拉斯特征映射，作为输出层的正则项，以提高KRVFL模型的地物识别精度。

1 研究方法

1.1 高光谱图像空谱信息特征提取

ERS算法的核心是图论思想［10］，其熵率能促进高光谱图像分割形成结构均匀、紧凑的同质区域，仅覆盖图像中的单一目标，其工作流程如图1所示。

高光谱数据集形如X∈R，M、N、D分别代表其行、列和波段数。将X转变为二维矩阵X=［x，x，…，x］∈R，元素i的波谱为x（1≤i≤m），m=M×N。首先对X进行主元分析，提取其第一主成分Υ，由Υ的像素点构造无向图G=（V，E），其中V为Υ构成的超像素点集，E为相邻超像素点的边构成的集合，即采用带权的无向图G=（V，E）代替源图像，把图像从分割问题转化为划分问题。最优化目标函数为：

c*=arg｛F（c）+θE（c）｝    （1）

其中，c*为E中的子集c所对应的最优值；F（·）为随机游动熵率；E（·）为平衡项；θ为调节权重。

求解式（1）可得高光谱图像Υ被分割为：

Υ=L，L∩L=？芰，i≠j    （2）

其中，L和L为Υ中第i和j个超像素；m为Υ中的超像素数量。

1.2 高光谱地物识别模型

1.2.1 核随机向量函数连接网络（KRVFL）

RVFL网络是一个经典的单层前馈神经网络［11］，结构如图2所示。为了进一步提高模型的识别能力，将RVFL网络与核函数相结合，用核函数代替RVFL网络中隐含层的特征映射，构建KRVFL模型，由此将数据特征升维，使高光谱图像分类更加精准。此外，输入层和输出层之间的直接连接是一种简单有效的正则化技术，可防止RVFL网络数据过度拟合。

图2 RVFL结构示意图

｛（x，y）｜x∈Rn，y∈Rm，i=1，2，…，N｝为输入样本，即拥有p个增强节点的RVFL网络为：

Hω=Y         （3）

其中，H是输入层和增强层输出的串联矩阵；ω为输出权值向量；Y是输出标签矩阵。

H和ω表达式如下：

H=［H1；H2］        （4）

H=x … x ？埙 x … x

H=G（a·x+b） … G（a·x+b）    ？埙  G（a·x+b） … G（a·x+b）

ω=［ω … ω］   （5）

其中，G（·）为激活函数；a和b（j=1，2，…，p）是输入层和增强层间的权值和偏差。

图1中，输出权值可以直接通过Moore-Penrose伪逆计算得到，即：

ω=HY       （6）

KRVFL重新构造新的映射代替HH，则核矩阵Ω的计算式为：

Ω=HH=K       （7）

其中，K为核函数K（x，x）建立的核矩阵，i和j表征矩阵的元素位置。

为了增强KRVFL网络的鲁棒性，引入参数ρ，KRVFL的输出权值为：

ω*=H（Ω+ρI）Y     （8）

结合式（8），KRVFL模型输出为：

F（x）=h（x）ω*=［K（x，x1）…K（x，xN）］（Ω+ρI）Y （9）

1.2.2 流形正则化核随机向量函数连接网络（MR-KRVFL）

流形正则化的核心是将数据做映射处理并控制部分结构不变［12］。假设有两个样本x和x，它们拥有高度相似的分布特性，则在新的投影空间中y和y的距离应十分接近。目标函数为：

L=minw‖y-y‖     （10）

其中，w为样本x和x间的相似程度。

为了计算两个样本间的相似度，通常采用k近邻的方法，构建k近邻矩阵，而后基于高斯核函数计算其相似度。即：

w=

exp-，N（x，x）=1 and C（x）=C（x）

0    ，C（x）≠C（x）？摇（11）

其中，N（x，x）=1表示x与x两者相邻；σ表示高斯分布函数的标准差；C（x）=C（x）表示x和x为同一类别。

对式（10）作进一步推导：

L=w（yy+yy-2yy）

=wyy+wyy-2wyy

=2tr［Y（D-W）YT］

=2tr［YLYT］

（12）

其中，Y=［y，y，…，y］为训练样本的预测输出向量组成的矩阵，即L=D-W，D=w，L为拉普拉斯矩阵，D为对角矩阵。

根据上述推导分析，将流形学习理论思想引入KRVFL中，构造MR-KRVFL地物识别模型的目标函数为：

min D=‖β‖+‖Ω β-Y‖+tr（βΩLΩ β） （13）

对式（13）中的β求偏导可得：

=ρβ+（ΩΩβ-ΩY）+λΩLΩβ  （14）

其中，ρ是外部正则化系数；λ是流形正则化参数；L=L。

令式（14）为0，有：

β=（ρI+ΩΩ+λΩLΩ）ΩY    （15）

MR-KRVFL识别模型的输出为：

Q（x）=h（x）（ρI+ΩΩ+λΩLΩ）ΩY   （16）

2 融合空谱特征的MR-KRVFL高光谱地物识别模型构建

本研究提出了融合空谱特征的正则化核随机向量函数连接网络的高光谱地物识别模型，其构建流程如下：

a. 获取高光谱图像X并提取其第一主成分Υ；

b. 将ERS和PCA方法作用于X，确定超像素数量m，并提取空谱联合特征样本；

c. 将所获取的特征样本划分为训练集和测试集；

d. 设定MR-KRVFL模型的核函数类型，核参数γ、外部正则化系数ρ和流形正则化系数λ的值；

e. 将训练样本映射到KRVFL特征空间中，构建拉普拉斯矩阵L，由式（15）计算输出权值矩阵β；

f. 将测试样本作为地物识别模型的输入，得到高光谱图像分类结果。

3 实验结果与分析

3.1 实验数据和评价指标

采用两组高光谱遥感数据集作为实验对象，分别为Indian Pines和Pavia University高光谱数据集，即为对应的原始图（IP）（圖3）和标签图（PU）（图4）。IP由AVIRIS拍摄于美国印第安纳州西北部的农业试验场，空间尺寸145×145，空间分辨率为20 m，拥有400～2 500 nm的200个通道波段，并去除了24个噪声波段；可分类像元10 249个，包含16种地物类别。PU在2003年由ROSIS拍摄于意大利北部的Pavia大学，空间尺寸610×340，用于标注作为高光谱图像地物识别测试用途，ROSIS的波长范围在0.43～0.86 μm，光谱仪共采集到115个波段，在实际应用中，去除带有低信噪比的12个波段，共取其他103个波段作为研究对象，空间分辨率可以达到1.3 m，包含9类地物，总样本点共记42 776个像元。

评价指标采用总体分类精度（Overall Accuracy，OA），平均分类精度（Average Accuracy，AA），第i类分类精度（Class-specific Accuracy，CA），Kappa系数［13］和混淆矩阵对分类结果进行綜合评价。

3.2 参数设定

笔者所提MR-KRVFL算法中，需要对5个参数进行设定分析，分别为超像素数量m、主成分数d、核参数γ、外部正则化系数ρ和流形正则化系数λ，其中核函数为高斯核函数。为了验证以上参数对OA值的影响，对于两个高光谱数据集，在{10-3，10-2，

10-1，1，101，102，103}上对γ、ρ和λ进行取值，设置对比实验。首先将ρ和λ在上述范围内随机选取，验证γ值变化时的影响，发现在IP和PU中，当γ为10-3时，整体分类效果最好。保持此条件，对ρ和λ对比分析，得到当ρ为10-2时，随着λ在上述区间内取值，OA值达到了最高，如图5所示，分别为IP在m取100、d取30、ρ取10-2时，λ变化对OA结果的影响，PU中m、d和ρ分别取60、30和10-2时，λ所对应的OA值。可以看出，当λ从10-3变为10-2时，其OA值增幅较大；在λ取10-1及之后，OA达到最高且趋于稳定。

图5 不同λ值对OA的影响

为了探索超像素分割算法中超像素数量m的选取对高光谱图像分类结果的影响，在IP和PU中分别对m在10～200区间内，间隔为10进行验证，在此保持其他参数不变。不同的主成分数d对高光谱图像分类精度的影响如图6所示，IP和PU分别在m取值区间为10～100和10～60之间，随着超像素数量m的增加，其空间信息逐渐丰富，OA快速提升，当其取到峰值后，随着m值进一步的增加，过多的空间信息开始对精度造成干扰，OA值开始缓慢下降。

从图6可以看出，IP在d取10～60，光谱信息逐渐丰富，OA逐渐增长，在d达到60之后，随着主成分数的进一步增加，OA的值趋于平缓且几乎无波动。PU随着d的增加，在d为30之后精度曲线的变

化缓慢增加，考虑到PU像素数目巨大，其地物分布更加密集，空间特征具有更高的利用率，综合d

图6 不同m和不同主成分数d对OA的影响

值对OA的影响，权衡之下d取30。

3.3 实验对比结果分析

本节选取了M-CNN［14］、RVFL、ELMCK［15］、CCJSR［16］和RMGE［17］5种分类模型进行对比实验，其参数设置与所提文献中一致，为了避免实验结果出现偏差，不同方法在IP和PU上分别进行10次重复实验，取其均值作为最终结果。同时，为了验证所提方法在小样本条件下的表现，统一将两个高光谱数据集的每类地物样本随机选取10%作为训练样本，其他全部作为测试样本。

表1列出了IP和PU不同方法对比实验的结果，可以看出笔者所提方法优于其他方法。在IP中，相较于RMGE方法，其分类指标OA、AA、Kappa值分别提升了0.86%、2.18%、1.34%，与CCJSR方法对比，OA、AA和Kappa值分别提升了5.65%、6.35%、6.20%，且笔者方法明显优于M-CNN、RVFL和ELMCK，印证了其高效性。同时，PU整体分类精度优于IP，这是因为IP数据样本分布不均匀，图像分辨率低，而PU样本数据量大，分布密集，空间利用率高。笔者方法对比CCJSR、RMGE和ELMCK，其分类指标OA、AA、Kappa值分别提升了2.38%、4.33%、4.96%，1.65%、3.09%、2.15%和4.29%、8.29%、6.38%，相较于其他经典算法，分类指标都得到了提升。

IP和PU不同模型所对应的识别效果分别如图7、8所示。由图中可以看出，两个高光谱数据集在笔者所提方法MR-KRVFL下，其实际效果图与真实标签图最为接近，各区域相对平滑，错分点最少。而M-CNN和RVFL方法所生成的识别图像产生了较为严重的多样本混叠现象，误分点较多，且分布杂乱无章，ELMCK、CCJSR和RMGE方法虽然相比而言得到了一定程度的改善，但在小区域内还是存在像素点误分的情况，整体表现依然欠佳。

综合上述实验结果，证实所提方法充分利用了空谱特征，获得了较优的分类结果。

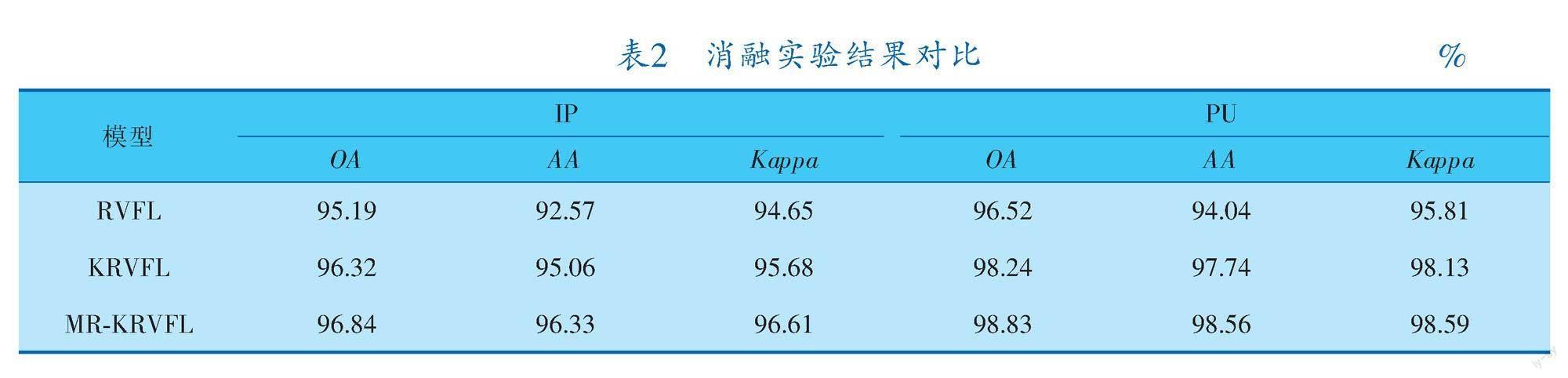
3.4 消融实验

本节设计验证MR-KRVFL地物识别模型的有效性。在ERS与PCA结合的超像素特征提取方法下，分别采用RVFL、KRVFL和MR-KRVFL地物识别模型对两个高光谱数据集IP和PU进行实验对比，其对应的分类指标见表2。在IP中，MR-KRVFL地物识别模型相比较KRVFL和RVFL模型的分类指标OA、AA和Kappa值分别提升了1.65%、3.76%、1.96%和0.52%、1.27%、0.93%，印证了引入核函数使空谱特征输出更加稳定，而流形正则化约束更加注重样本间的结构信息，提高了地物识别模型的性能，特别是在IP这种本身分辨率较低的高光谱数据集中，同样取得了较好的效果。观察PU发现，笔者所提模型相较于RVFL和KRVFL模型，其分类指标OA、AA、Kappa值分别提升了2.31%、4.52%、2.78%和0.59%、0.82%、0.46%，虽然在不添加流形正则化约束的KRVFL模型中，其分类性能已经达到较高水平，但经多次实验结果表明，流形正则化的加入依然提高了其分类精度。

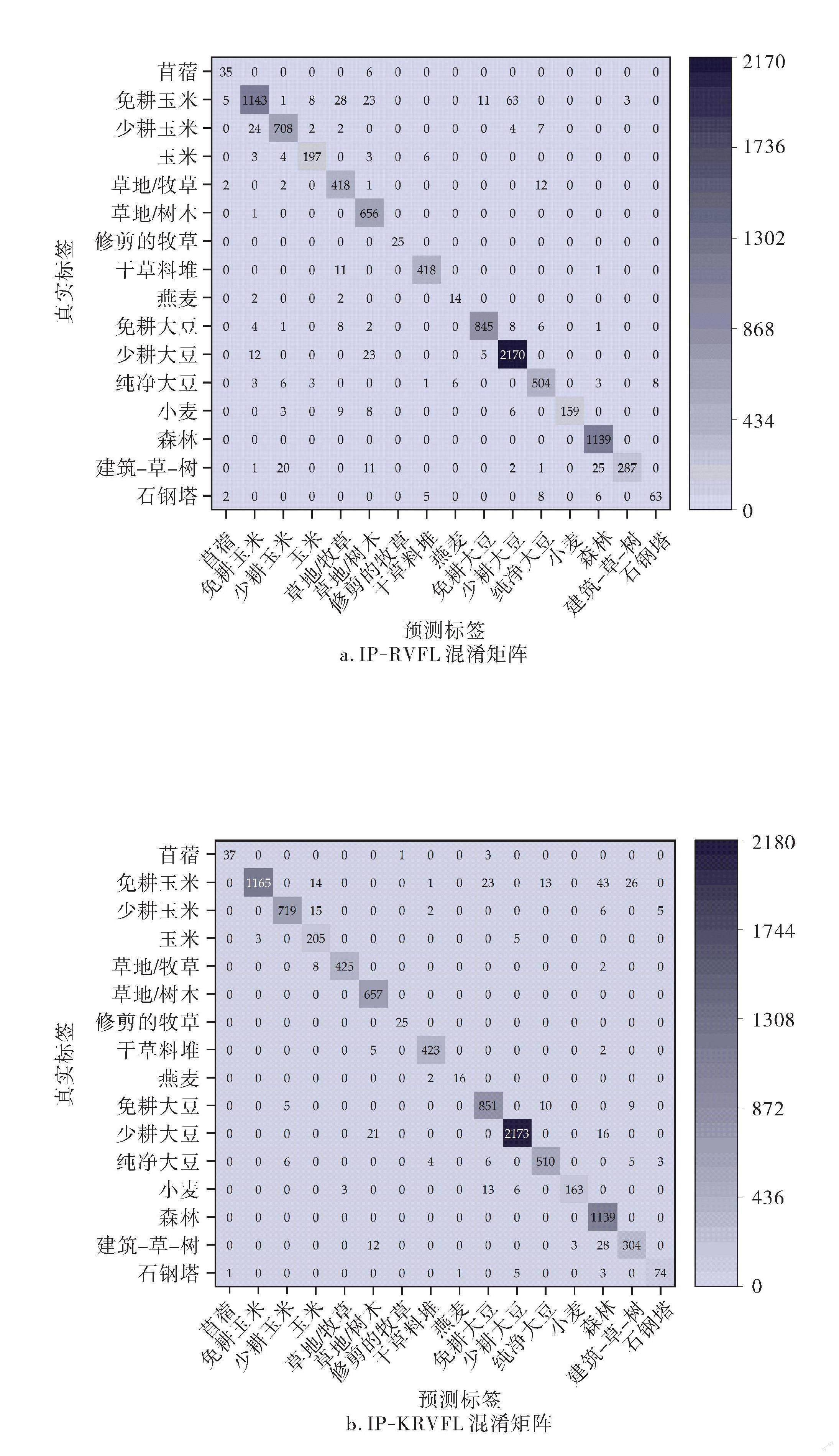
表征IP和PU对应的RVFL、KRVFL和MR-KRVFL地物识别模型分类效果的混淆矩阵可视化图如图9所示，对角线即为正确分类的样本数，其他位置为错分样本数。可以看出，笔者所提模型对于各个样本类别的识别错分数量最少，正确识别样本数量相较于RVFL和KRVFL方法进一步增多。证明笔者模型能够有效提升高光谱地物识别模型的分类性能。

4 結束语

融合空谱特征的MR-KRVFL地物识别模型充分利用空间像素的结构信息，获取了良好的地物识别效果。在MR-KRVFL模型中核函数避免了其随机参数特性，有效加强了输出神经元的稳定性，提高了分类精度，将流形正则化约束作用于KRVFL模型，进一步增强了模型的泛化性能。实验证明，MR-KRVFL地物识别模型在Indian Pines和Pavia University两个高光谱数据集上表现出优越的性能，较其他方法更为出色。该模型在高光谱图像分类问题上有良好的表现，因此可以为分析工业材料的成分、纯度、形态及缺陷等提供有益借鉴。

参 考 文 献

［1］ GORE R，MISHRA A，DESHMUKH R.Exploring the mineralogyat lonar crater with hyperspectral remote sensing［J］.Journal of the Geological Society of India，2021，97：261-266.

［2］ 冯权泷，牛博文，朱德海，等.土地利用/覆被深度学习遥感分类研究综述［J］.农业机械学报，2022，53（3）：1-17.

［3］ 赵庆展，江萍，王学文，等.基于无人机高光谱遥感影像的防护林树种分类［J］.农业机械学报，2021，52（11）：190-199.

［4］ HE N J，FANG L Y，LI S T，et al.Feature extraction with multiscale covariance maps for hyperspectral image classifition［J］.IEEE Transactions on Geoscience and Remote Sensing，2019，57（2）：755-769.

［5］ TU B，ZHOU C， LIAO X，et al.Spectral-spatial hyperspectral classification via structural-kernel collaborative representation［J］.IEEE Geoscience and Remote Sensing Letters，2021，18（5）：861-865.

［6］ 虎晓红，司海平.基于自适应字典的小样本高光谱图像分类方法［J］.农业机械学报，2021，52（1）：154-161.

［7］ JIANG J，MA J，CHEN Z，et al.SuperPCA：A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery［J］.IEEE Transactions on Geoscience and Remote Sensing，2018，56（8）：4581-4593.

［8］ YU X，FENG Y，GAO Y，et al.Dual-weighted kernel extreme learning machine for hyperspectral imagery classification［J］.Remote Sensing，2021，13（3）：508.

［9］ 张政煊，杨翊卓，代伟，等.基于整体辨识策略的非线性自适应控制方法［J］.控制理论与应用，2023（11）：2039-2048.

［10］ LIU M Y，TUZEL O，RAMALINGAM S，et al.Entropy-Rate Clustering：Cluster analysisvia maximizing a submodular function subject to a matroid constraint［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36（1）：99-112.

［11］ PRATAMA M，ANGELOV P P，LUGHOFER E，et al.Parsimonious random vector functional link network for data steams［J］. Information Sciences，2017，430-431：519-537.

［12］ ZHAO H，ZHENG J，DENG W，et al.Semi-supervised broad learning system based on manifold regularization and broad network［J］.IEEE Transactions on Circuits and Systems I-Regular Papers，2020，67（3）：983-994.

［13］ LI R，ZHENG S，DUAN C，et al.Classfication of hype- rspectral image based on double-branch dual-atttention mechanism network［J］.Remote Sensing，2020，12（3）：582-607.

［14］ HAMIDA A B，BENOIT A，LAMBERT P，et al.3-D deep learning approach for remote sensing image classification［J］.IEEE Transactions on Geoscience and Remote Sensing，2018，56（8）：4420-4434.

［15］ ZHOU Y，PENG J，CHEN C.Extreme learning machine with composite kernels for hyperspectral image classification［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2015，8（6）：2351-2360.

［16］ TU B，ZHANG X，KANG X，et al. Hyperspectral ima- ge classification via fusing correlation coefficient and joint sparse representation［J］.IEEE Geoscience and Remote Sensing Letters，2018，15（3）：340-344.

［17］ MIAO Y，CHEN M，YUAN Y，et al.Hyperspectral ima- gery classification via random multi-graphs ensemble learning［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2021，99：1-11.

（收稿日期：2023-05-08，修回日期：2023-05-20）

Research on Hyperspectral Ground Object Recognition Model of

MR-KRVFL Based on Space Spectrum Features

GUO Guo-lu1，2 ， FAN Yu-gang1，2， FENG Xiao-su1，2

（1. Faculty of Information Engineering and Automation ， Kunming University of Science and Technology；

2. Key Laboratory of Artificial Intelligence of Yunnan Province）

Abstract   Considering the fact that the complex spatial spectrum characteristics of hyperspectral images influence the classification accuracy of ground object recognition model， a manifold regularization kernel random vector function network （MR-KRVFL） method for hyperspectral image recognition based on spatial spectrum features was proposed. Firstly， having the hyperspectral image segmented by super-pixel with entropy rate（ERS） to obtain corresponding homogeneous regions; and then having the spatial spectral joint features extracted by principal component analysis （PCA） to reduce dimension of the homogeneous regions; and finally having the spatial spectrum feature information based to construct the kernel random vector function connected network（KRVFL） model and having the manifold regularization constraint applied to improve the generalization performance of the ground object recognition model. Applying this model to the hyperspectral data sets of Indian Pines and Pavia University shows that， the classification accuracy can reach 96.84% and 98.83%， which proves the validity of the model proposed.

Key words   entropy rate super-pixel segmentation， hyperspectral image， kernel function， manifold regularization， classification accuracy， ground object recognition