核心素养下初中数学教学中的德育渗透对策分析
2024-04-24刘璐
刘 璐
(淄博市张店区实验中学,山东 淄博 255000)
在素质教育的背景下,成绩已不再是衡量学生能力的唯一标准,社会各界和学校逐步开始重视学生的道德品质和价值观念的发展。随着教育体制改革和核心素养的落实,教师作为课堂组织者,也要在课前预习、新知学习、习题练习等多个教学环节,有意识地渗透德育内容,引导学生形成良好的学习习惯和严谨的思维方式。
一、初中数学教学中渗透德育的意义
在初中数学课堂教学中渗透德育,对学生学习和成长都有着重要意义。但德育落实过程中仍存在不足,有些数学教师认为德育是班主任和思想品德教师的责任,与数学教学没有直接关系,但其实数学中也蕴含着丰富的德育内涵,是培养学生良好品质的重要媒介。《义务教育数学课程标准(2022 年版)》中提出,教师在教学中要注重培养学生高尚的品德、远大的理想,助力学生正确审美和价值观念的形成。由此可见,在初中数学课堂中渗透德育,是新时代教育的基本要求,更是学生发展的真实渴望。另外,初中生处于青春期,生理和心理的成长会带动情绪方面的变化,影响其性格和道德品质的形成。若教师在教学中只注重提升学生的学习成绩,忽视对学生道德品质的培养,学生的人格塑造容易受到影响,甚至在外界的不良诱惑下走入歧途,这对学生未来的成长是非常不利的。有效的德育渗透能解决以上问题,在课程教学中潜移默化地向学生传递优秀的道德品质,提升数学教学效果的同时促进学生健康成长。
二、核心素养下初中数学教学中渗透德育的策略
(一)预习环节:导学中渗透德育,培养数学感知素养
预习是数学课堂教学的重要环节,对锻炼学生自主学习能力有着积极作用。数据分析是初中数学核心素养的重要组成部分,教师应以这一要求为导向精心设计预习导学案,利用数学问题激活学生的数学感知思维,让其在探究中初步感知新知识。这一过程中,教师可以搜集数学史、数学故事等内容,在丰富学案的同时拓宽学生的视野,有效向其传递人文精神。
以鲁教版数学八年级下册《二次根式的加减》的教学为例,教师应在确定教学目标后,为学生制定预习导学案。首先,教师结合教学经验和学生能力,将教学目标制定为:了解二次根式的加、减运算法则,能运用其进行简单的计算,且能将分母中含有二次根式的式子进行分母有理化。而后,再根据教学目标在导学案中提出问题:现有一块长为7.5 分米、宽为5 分米的木板,能否在其中分别截出8 平方分米和18 平方分米的正方形木板?这一问题是典型的二次根式加法运算问题,要求学生画出图形后并尝试解答,能充分强化其数感。随后,为了避免部分学生思路受阻,教师应在导学案末尾为其留下“线索”,如判断能否截出两块正方形木板,需要判断木板的长和宽是否大于两块正方形木板边长之和。学生根据这一提示列出,并通过化简将其整理为最简二次根式,再运用分配律尝试求出结果。由此,解决问题的过程就是学生自主探究新知的过程。最后,教师在导学案中给出关于“二次根式”的阅读材料,让学生通过阅读了解数学史,辅助深化对二次根式的理解,从而让学生在有效的预习时间内获得更多的数学知识,实现智育和德育的深度融合。
(二)课堂教学:授新中渗透德育,培养深度学习素养
1.创设德育情境,强化抽象素养
学生在学习和理解知识时,思维有一个过渡过程,教师在教学中要遵循学生的认知规律,选择恰当的方式引入新知。情境教学法常用于引入新知,其有着形式丰富、内容直观的优点,能有效丰富学生的学习体验,提高学生科学探究的积极性。对此,教师应在教学过程中渗透德育情境,再提出具体的问题,引导学生在探究和分析中提炼出数学概念,降低数学学习的难度。同时,德育内容的渗透还能助力学生对数学学习形成积极的情感态度。
以鲁教版数学八年级上册《中心对称》的教学为例,为了培养学生的抽象思维,教师可在课堂中创设德育情境。首先,教师利用多媒体展示京剧脸谱、蝴蝶标本、风车等图形,让学生在观察中了解我国优秀的传统文化,而后,教师提出问题:“京剧脸谱、蝴蝶标本、风车都有什么特征?”部分学生下意识地回答:“都是轴对称图形。”教师要求其再次仔细观察,学生发现“京剧脸谱和蝴蝶标本是轴对称图形,但风车并不是”,进而产生疑惑。由此,借助文化情境拉近学生与艺术之间的距离,并利用矛盾认知激发学生的求知欲,高效引入新知识内容。随后,教师将风车图片放大,并适时引入“中心对称”概念,让学生找出风车的对称中心,从而自行总结中心对称图形的特征。最后,教师再展示其他中心对称图形,要求学生结合情境中的感悟,找出其对称中心,如圆是中心对称图形,它的对称中心就是圆心。在此情境下,学生不仅可以了解我国源远流长的戏剧文化,还能在对比中认识到“中心对称”这一新知,文化素养和抽象思维均能得到加强。
2.开展合作讨论,培养推理素养
合作能力是当前评价人才的重要标准之一,教师在课堂中组织合作讨论活动,能在突出学生主体地位的同时锻炼其协作能力。在实践教学中,教师应结合教学主题为学生布置讨论问题或任务,让学生在探究欲望的驱动下参与到讨论之中,并在与成员交换想法、总结规律的过程中形成良好的逻辑推理素养。
以鲁教版数学八年级下册《菱形的性质与判定》的教学为例,为了强化学生的逻辑推理素养,教师应结合教学重难点开展小组合作学习活动。首先,教师在课堂中结合学生的数学能力和核心素养,进行科学、合理的分组,而后要求各小组制作一个“菱形”模型,先通过观察说出菱形有哪些特点,各小组成员积极展开讨论,有人说“菱形是特殊的平行四边形”,有人补充说“有一组邻边相等的平行四边形是菱形”等。由此,在小组互动中,所有学生都能参与到数学探究过程中,并在交流和协作中初步归纳和整理菱形的性质。随后,在合作讨论的过程中,教师利用问题引导探究方向:如果说菱形是平行四边形,那么它具有平行四边形的哪些性质呢?让各小组通过折叠、旋转等操作,对菱形的边、角、对角线、对称性等展开更深层次的探究。这一过程中,教师要给予学生充足的探索和交流时间,让学生在具体操作中获得知识,强化学习效果。最后,各小组依次上台阐述合作探究结果,再以板书的形式呈现菱形的性质。学生通过小组通力合作,主动完成了对菱形性质的分析和掌握,并在过程中形成了良好的合作意识。
(三)习题教学:分析中渗透德育,提升数学运算能力
1.利用例题培养解题能力
运算能力是学生必须掌握的一项能力。学生受思维能力、数学基础等因素影响,运算能力存在明显差异。核心素养背景下,教师传授学生解题方法和技巧后,还要注重启发学生的思维,使学生领悟解题方法中蕴含的数学思想。对此,教师应结合学生的能力设计具有代表性的习题,引导学生通过探究典型问题强化解题能力。同时,教师还可以在解题过程中抓住机会渗透德育,如学生思维受限、解题失败时,给予其鼓励和支持,助力学生核心素养成长的同时落实德育目标。
以鲁教版数学八年级下册《一元二次方程根与系数的关系》的教学为例,为了深化学生对“韦达定理”的理解,教师应在课堂中利用例题培养学生的解题能力。具体内容如下:
【例题1】已知关于x 的方程①x2-(1-2a)x+a2-3=0有两个不相等的实数根,且关于x 的方程②x2-2x+2a-1=0 没有实数根,问a 取什么整数时,方程①有整数解?
【例题2】不解方程,判断方程2x2+3x-7=0 两个根的符号。
以上是学生解一元二次方程中经常遇到的问题,具有一定的代表性。教师在指导学生解题前,要先对题目展开分析,如解决例题1 时,a 的整数值需要同时满足方程①②的条件,“一元二次方程存在实数根”是破题的关键,确定a 的取值范围后,再依靠解不等式相关知识进行推理。而解决例题2 时,需要利用韦达定理求出判别式的值,再分别确定x1·x2或x1+x2的正负情况,将“根的判别式”与“根与系数的关系”结合起来灵活运用,进而得出正确答案。随后,教师给予学生一定的解题时间,让其结合分析内容尝试独立解题,再针对解题中遇到的问题进行有效讲解。如部分学生解决例题1 时,根据韦达定理求出,因为方程②没有实数根,所以,解得,于是,同时满足方程①②条件的a 的取值范围为,又因为a 取整数值,所以a=2 或a=3。很明显,学生理解了教师讲授的解题思路,但思维不够严谨,缺少对解的验证过程。对此,教师应给予有针对性的指导,让学生将各个解代入方程①中,发现a=2 时,方程①没有整数根,当a=3 时,方程①有整数根。学生纠正错误后,教师要鼓励学生遇到问题坚持到底,不要为了简便省略步骤。通过例题的讲解,学生能对一元二次方程根与系数的关系产生更深刻的认识,促进其运算能力和逻辑思维的成长。
2.通过纠错培养抗压能力
《左传》中说:“人谁无过,过而能改,善莫大焉。”这句话同样适用于学生学习数学的过程。无论是课堂问答、完成作业还是考评测试中,错误都是难以避免的。教师不要在学生犯错时过多谴责,而是要引导学生正视错误并积极寻找改正错误的渠道,从而在识错、纠错中促进思维和能力的进步。核心素养背景下,教师应积极整理学生易犯错的知识点或题型,有针对性地展开纠错教学,让学生在总结和反思中认识到错误的原因和解决途径,实现查缺补漏。这一过程中,教师还可以引入“抗挫”案例,保护学生学习数学的自信心。
以鲁教版数学八年级下册《一元二次方程的应用》的教学为例,教师可以结合学生课后作业的完成情况,整理其易错题并开展纠错教学。具体内容如下:
【易错题】如图1 所示,某长方形硬纸片长为40cm,宽为25cm,将角上的四个小正方形裁剪掉后,折成了一个无盖纸盒,若纸盒的底面积是450cm2,则纸盒的高为多少?
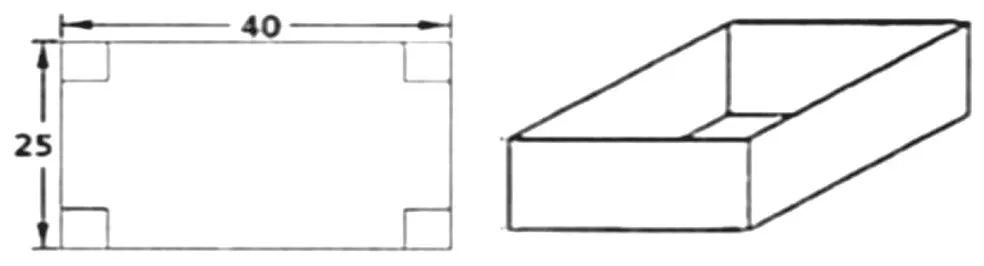
图1
教师统计学生的解题情况,发现存在“未知数x不准确”“所列方程错误”“等量关系错误”“所求答案不符合题意”等问题,如本题应将纸盒的长设为x,高设为(40-x)÷2,但某些学生的空间转换能力较差,寻找等量关系时列出高为(40-2x)的错误式子。还有部分学生将纸盒的高设为x,列方程为(40-2x)(25-2x)=450,求出x1=5 和x2=27.5,却未对两个解进行检验,导致其中一个解不符合题意。在纠错教学中,有些学生的主观态度也不积极,常常不愿意面对自己的错误。针对这一情况,教师要合理渗透德育内容,通过讲述一些数学家在研究中出现错误的案例,让学生认识到犯错是常态,在学习中努力做到不犯相同的错误即可,让学生客观看待错误,形成“失败是成功之母”的正确态度,并在纠错、改错中提高解题能力。
三、结束语
核心素养视域下,初中数学教师要加强德育,同时在课程教学中寻找落实机会,以满足学生的成长需求。课堂教学中,教师要整合数学教育资源,包括习题、数学史等内容,再运用情境教学、小组合作教学、动手实践等多种方式,潜移默化地渗透德育,助力学生形成良好的道德品质和价值观念,为其学习和成长保驾护航。
