LDA和KNN算法在随钻测井火成岩分类的应用
2024-04-24方全全曹军张国强许吉俊任宏
方全全,曹军,张国强,许吉俊,任宏
1.中海油能源发展股份有限公司工程技术分公司(天津 300451)
2.中海石油(中国)有限公司天津分公司工程技术作业中心(天津 300451)
0 引言
渤中34-9油田表现为一个复杂断块构造,位于黄河口凹陷中洼南部斜坡带上,在明化镇组、东营组和沙河街组形成了大型复杂断块圈闭群。已钻井揭示了在沙河街组与东营组存在多期火山活动,该区钻遇的火成岩分布广泛但不连续,岩石类型多样。其中又以玄武岩、安山岩、沉凝灰岩等中-基性火成岩与火山碎屑岩最为典型。此外,在油田开发过程中广泛采取随钻4 条线(自然伽马、电阻率、中子、密度)的测井方式录取测井资料[1-2],实现了全区测井数据的可对比性与标准化。常规任取2条测井曲线(如伽马、密度)进行两两交会的方式划分火成岩岩性精度较差,故有必要对该区进行多参数综合分析岩性评价。
线性判别分析(LDA)与K最近邻(KNN)方法是当前比较流行的监督式机器学习方法[3-4]。刘得芳等应用决策树方法提高了利用单一信息判别的准确性[5],张银德等结合测井资料和试采资料利用支持向量机方法准确识别了油、气、水层[6],展示了机器学习方法在油气勘探的巨大潜力。通过对目标区5口评价井的随钻测井数据进行多元线性判别分析,4条测井曲线降维至平面坐标系,建立了二维可视化岩性识别图版。另外通过与KNN 分类模型的结合,减少了欧式距离计算量并提高了分类模型的准确性,取得了良好的应用效果。
1 LDA和KNN分类方法原理
线性判别分析(LDA)是一种常用的判别、分类的多元统计方法,其基本原理是使用统计学及机器学习方法,在多维特征空间中寻找物体或事件特征的最佳线性组合,即空间投影向量[7]。该投影向量能够特征化或区分样本数据,作为一个线性分类器将待分类的对象与已知类型的对象进行对比,根据最大隶属原则划分待判对象的归属。
KNN方法的基本思路是:事先给定常数K(通常为奇数),在特征空间中如果距离待分类样本最近的K个样本中的大多数属于某一个类别,则该待分类样本也属于这个类别[8]。
1.1 数据收集与预处理
通过前期研究,收集BZ34-9区块5口评价井并统计了钻遇的厚层、典型的与火山成因相关的岩层如下:沉凝灰岩、玄武岩、安山岩、凝灰质砂岩、凝灰质泥岩、玄武质泥岩。对于后3种砂泥岩,结合常规岩屑录井与测井响应特征区分度高,能够很好识别。故筛选出沉凝灰岩、玄武岩、安山岩共计3 258个数据样本(其中1 927个沉凝灰岩样本,1 100个玄武岩样本,232 个安山岩样本),将每个样本写成向量形式x=[x1,x2,x3,x4],x1~x4分别表示样本的4个特征,(自然伽马、电阻率、中子、密度),样本数据见表1。预处理阶段对原始4 条线的测井数据做归一化处理,归一化公式见式(1)[9]。归一化前、后的样本数据统计指标见表2。
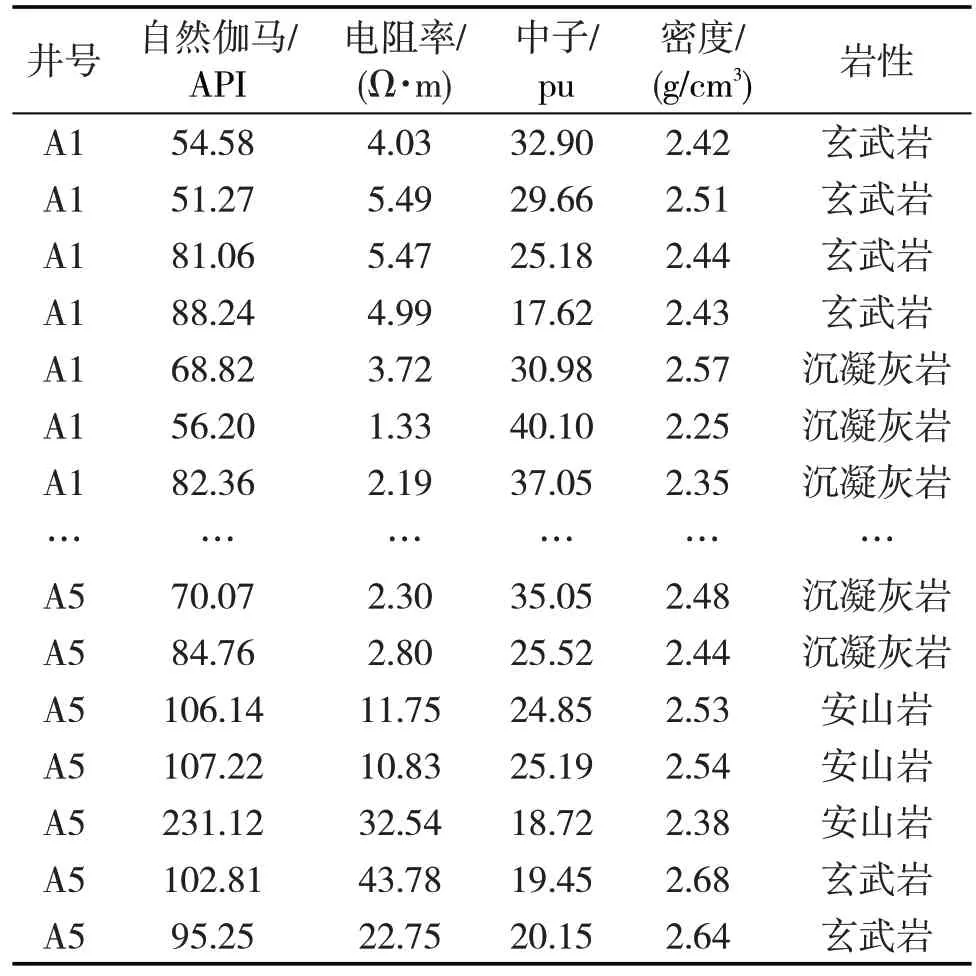
表1 基于随钻4条线测井数据构建的样本数据集
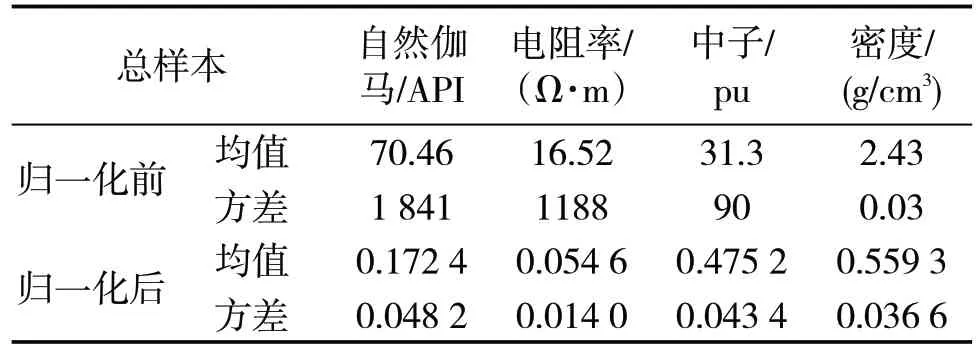
表2 样本数据基本统计指标
1.2 线性判别分析与KNN处理过程
线性判别分析的目标是在特征空间中寻找最能把各类样本区分开的投影向量,这要求投影后的同类样本簇更聚集和紧凑,且不同类别的样本簇之间尽可能远离。统计学中用类间散度(Sb)描述不同类别样本簇之间的远离或区分程度,用类内散度(Sw)描述同类别样本簇之间的聚集程度。根据样本类间散度和样本类内散度的比值(Sw-1×Sb)最大的目标选择线性变换矩阵W[10]。对目标矩阵Sw-1×Sb进行特征值分解,选取较大的特征值对应的特征向量即为做投影的线性变换矩阵W。以常见的c分类问题(c≥2)定义Sb、Si和Sw矩阵分别为:
式中:N表示总样本数;μi表示第i类样本的均值,μ为总样本均值;Ni为第i类的样本数;xik为第i类的第k个样本;c表示类别数;Si为第i类样本的类内散度。从公式上看散度的定义与协方差矩阵的效果一致:协方差越大表明样本越分散,类间或类内散度也越大。
KNN 所选择的距离最近样本是已经正确分类的对象,根据最邻近的K个样本的类别来决定待分样本所属的类别,这是一种多数表决的分类决策规则,在最优化理论中多数表决规则等价于经验风险最小化,也即模型的误分类率最小[11]。通常使用欧几里得距离作为样本之间距离的衡量指标,n维空间中样本xi到样本xj的欧式距离定义如下:
式中:xik指样本xi的第k个维度(特征)。实践中K取奇数,避免出现K个样本中恰有的样本隶属于不同类别而无法分类决策。由于KNN 方法主要依赖周围有限的K个邻近的样本,避免了依靠判别类域的方法来确定所属类别,因此对于类域的交叉或重叠较多的待分样本集,KNN方法效率更高。KNN主要步骤如下:
1)将总体样本划分为训练样本(带类标签)与测试样本(未知所属类别)。
2)对于每个待测试样本,根据式(5)计算其到每个训练样本的距离。
3)选择距离最近的K个训练样本,并分别统计K个样本中属于各类的个数。
4)K个样本中出现最多的类别决定了该测试样本所属类别。
2 应用实例
使用开源软件python的numpy库和pandas库对3 258 个样本归一化后的数据样本进行判别分析。总样本具有4 个维度(每条测井曲线看作一个维度)。由线性判别分析的基本原理可知:对于划分N类的情况,线性判别分析处理之后可将数据降至N-1维度。本文区分3类岩性,因此经线性判别分析处理后样本数据呈现2 维特征,可以利用交会图的形式呈现分类效果。
使用numpy 包的np.linalg.svd 函数对目标矩阵Sw-1×Sb做特征值分解,取非零特征值对应的特征向量组成投影向量记作B,将沉凝灰岩、玄武岩、安山岩对应的归一化后的测井数据以此投影向量做线性变换(X×B,X为3 258 行/4 列,B为2 行/4 列),原始的4维测井数据降至2维,记为B1,B2,见表3。其中GR,RT,CN,DEN 分别表示预处理后的自然伽马、电阻率、中子与密度值。
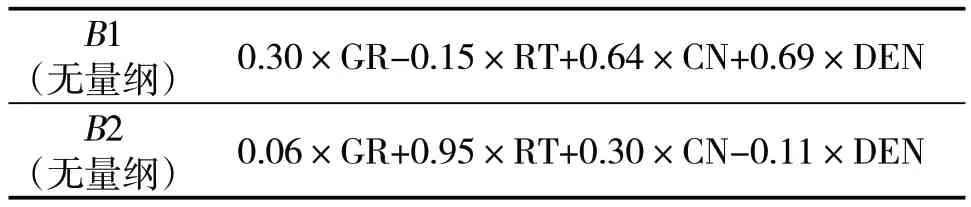
表3 线性判别降维结果
以B1,B2 分别作为横、纵坐标绘制2 维可视化解释图版(图1)。在图1 中,3 类岩性区分度很高,安山岩最易于区分开来,玄武岩与沉凝灰岩利用设定B2阈值的方式也能很好区分,但阈值两侧仍存在一些误分类点,这是由于在岩性界面测井曲线突变或剧烈波动造成的,针对这种现象,有必要通过KNN方法将分类距离定量化,消除阈值设置的主观性与不确定性。
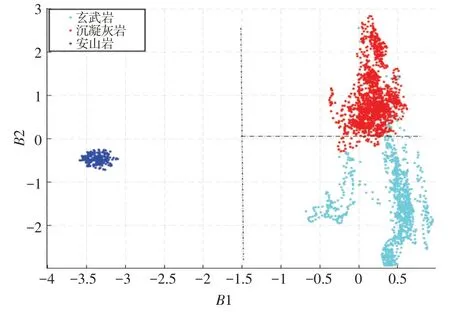
图1 线性判别二维可视化图版
K 近邻方法需要对样本数据做贴标签处理:首先将样本数据划分为训练集与测试集,见表4。在给定的训练数据集(已知类标签),对于新输入的实例(测试样本,待分类)在数据集中找到与该实例最近邻的K个实例,以K个实例中的多数类别赋予待分类实例。对于欧式距离的计算,分别在两种空间维度上进行:方式1,4 维空间上使用原始4 条线测井数据(预处理后);方式2,2 维空间上使用判别分析投影后的B1 和B2。相较于前者,后者的距离计算能节省一半的计算量,这也体现了将线性判别分析与KNN方法融合的一项优势。

表4 数据集构建方式
将两种维度空间上的距离计算分别代入KNN原理步骤1,综合考虑计算时效与精度实践,取K=5(即只观察距离待分类样本最近的5个样本),3种岩性类别分别赋予类别标签:“1=玄武岩,2=沉凝灰岩,3=安山岩”,最后画出杆状图显示分类结果,如图2所示。
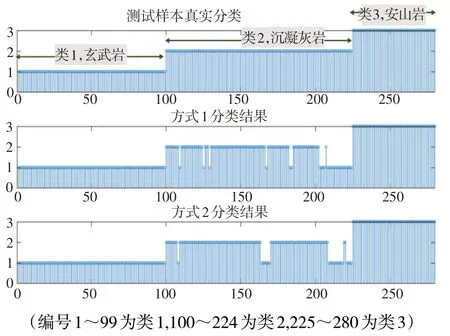
图2 两种方式KNN分类结果对比
由图2 可见,KNN 分类模型在类1、类3 识别准确率很高,即可以较好地区分玄武岩与安山岩,错误分类主要集中在类2(沉凝灰岩)的识别上,具体分类结果与分类评价指标见表5。

表5 两种方式分类效果
对比两种方式下模型分类能力的主要评价指标,结果显示,以自然伽马、电阻率、中子、密度4 条线预处理的测井数据作为KNN模型的输入(方式1)其分类正确率为90.36%;而以线性判别分析后的数据B1,B2作为KNN模型输入(方式2)其分类正确率为92.50%。综合分类正确率与召回率两个评价指标,方式2 的分类模型优于方式1,且方式2 的分类模型减少了欧式距离的计算量。
3 结论
1)多元线性判别方法克服了常规多参数火成岩岩性识别的局限性与多解性。本文建立的基于线性判断分析火成岩分类交会图版有助于现场利用随钻测井数据快速、准确识别岩性。
2)融合LDA 与KNN 技术建立了区块火成岩的分类模型,模型分类正确率达到92.50%,在降低原始KNN 模型距离计算量的同时提高了岩性分类准确率。
3)KNN模型中的K值选取则依赖经验。K值很大会增加计算量同时造成模型的欠拟合;K值太小会造成模型的过拟合。最后,不同机器学习方法的适用环境与应用目的侧重不同,需要结合问题有针对性地设计模型,通过有机地融合机器学习的不同方法建立高效、稳定、泛化能力强的模型是今后应用的一个重要方向。
