基于蒙特卡洛方法的配电网线路雷击跳闸率计算

2024-04-23陈雅芳

电力安全技术 2024年3期

陈雅芳

(广州中光电气科技有限公司，广东广州 510530)

0 引言

由于配电网线路绝缘水平低,由雷击引起的线路跳闸事故时常发生[1]。目前针对配电网线路雷击跳闸率计算的研究比较多,如文献[2]基于规程法进行雷击跳闸率的计算,但规程法是基于普遍性原则的方法,在针对具体地区线路时该方法欠缺准确性；文献[3]基于电气几何模型与雷电流幅值的概率分布推导了引雷范围的计算公式,但不同地区地闪密度的差异性给计算结果带来一定的误差。蒙特卡洛方法是用随机数或者伪随机数来解决问题,优点是符合实际雷击过程的随机性。但雷击过程中的随机因素众多,如文献[4]对雷电流幅值、落雷位置、工频电压瞬时值等因素进行了随机模拟,有些学者还考虑了波头时间的影响[5]。因此,选取哪些随机过程进行模拟以及如何建模模拟,都会影响到蒙特卡洛方法计算雷击跳闸率的确信度和速度[6],目前对于随机过程如何选取以及雷击闪络判据尚无统一标准。针对以上问题,采用蒙特卡洛方法进行雷击跳闸率计算,并考虑线路屏蔽因子,结合雷电流幅值概率密度的拟合曲线进行对比分析,以期为配网线路雷击跳闸率的计算分析提供参考。

1 蒙特卡洛计算方法

1.1 计算流程

雷击跳闸率的计算涉及到地闪密度、闪络率、建弧率三个重要参量。

式中,η为雷击跳闸率,次/(100 km·年）；Ng为雷电活动强度的地闪密度,次/(km2·年）；S为引起线路跳闸的有效受雷区域,km；ξ为闪络率；σ为建弧率。

闪络率的计算需要重复模拟雷击过程并判断是否闪络,其中单次循环过程中是否达到闪络条件是由雷电流幅值I、落雷位置A0、线路瞬时电压U0、雷击线路位置B0(实际循环过程中用g模拟)以及雷电流极性I±共同决定,计算如下。

若满足闪络条件,则y=1,否则y=0。

假设模拟总次数为m次,当m足够大时,可得到线路雷击闪络率的估计值。

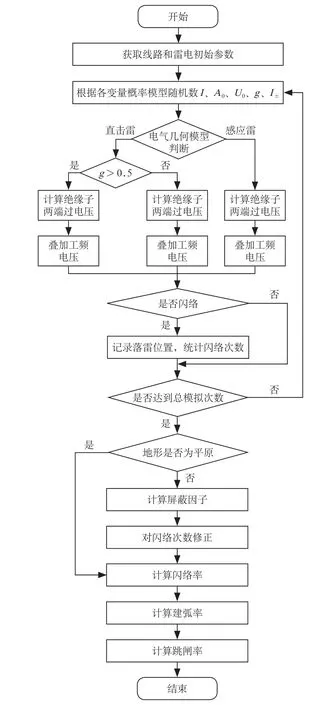
图1 蒙特卡洛方法计算雷击跳闸率的流程

1.2 随机数的生成

1) 雷电流幅值I。单次循环中,各变量的取值需要遵循一定的规则。可以由随机变量x的概率密度函数fx(x)求出分布函数Fx(x),然后求反函数,得到概率分布函数为Fx(x)的伪随机数。IEEE推荐模型的雷电流幅值概率分布函数如下。

式中,α与β为分布参数,可通过非线性最小二乘法拟合得到。

对上述概率分布函数求反函数,通过计算机产生在[0,1]上均匀分布的随机数t,获得满足概率分布的雷电流幅值。

2) 雷电流极性I±。雷电流极性I±按雷电流幅值的正负比进行取值[4]。根据地区统计,雷电流极性正负比为1∶3.87,通过计算机产生在[0,4.87]上均匀分布的随机数ω,若ω≤3.87,则取雷电流极性I±为负,否则取为正。

3) 雷电落雷位置A0。雷电落雷位置A0是随机的,单次雷击过程中,可以认为落雷位置A0在二维空间内是均匀分布的,如图2所示。lx为有效落雷区域宽度,ly为线路长度。4) 线路瞬时电压U0。线路瞬时电压U0应取与雷电极性相反的最大幅值相电压。三相工频电压瞬时值计算如下。

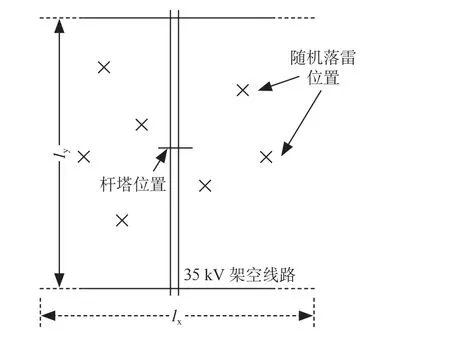
图2 随机落雷位置

式中,ψ为在[0,2π]上均匀分布的相角随机数。

5) 雷击线路位置B0。当某一落雷位置A0判定为直击雷时,又有反击和绕击两种情况,即雷击杆塔和雷击导线,因此需要对雷击线路位置B0进行模拟。计算时,通过计算机产生在[0,1]均匀分布的随机数g,当g小于某一值时,判定为雷击杆塔,否则为雷击导线。这一具体值应根据雷击中杆塔和导线的概率决定,对于配电线路,该值可取0.5。

1.3 过电压计算

由各随机变量下的过电压计算结果U决定了单次模拟过程是否达到绝缘闪络条件。

1) 直击雷情况下,雷击导线中央时,雷电经导线—杆塔—大地流向两侧,相当于并联的两条支路,过电压计算公式如下。

式中,UZ1为雷击导线过电压,kV；Zd为导线的波阻抗,工程计算中常取400 Ω。

2) 直击雷情况下,雷击杆塔时,雷电流经过杆塔和接地装置流入大地,过电压的计算如下。

式中,UZ2为雷击杆塔过电压,kV；R为接地电阻,Ω；Lt为杆塔等值电感,μH；h0为导线高度,m。

3) 感应雷情况下,过电压的大小与雷电流幅值I、落雷位置A0、导线高度h0相关,其简化计算公式如下。

式中,k为感应过电压系数,规程推荐k=25,lA为落雷点A0距线路的水平距离,m。

1.4 闪络次数的修正

若线路所处地形不是平原,还需要对得到的闪络次数进行修正,由于配电网线路耐雷水平较低,一般不架设避雷线,不架设避雷线的配电网线路电气几何模型如图3所示。rc、rt、rg分别为雷击线路、雷击树木和雷击大地的击距,b为被屏蔽弧段投影长度,h为导线平均高度,H、ltr分别为树木高度和距导线水平距离。弧CD是导线的暴露弧段。

图3 不架设避雷线的配电网线路电气几何模型

根据定义和图3中所示的几何关系,屏蔽因子Sf的计算表达式如下。

根据IEEE 1243—1997标准,击距的计算如下。

其中,Kg为地形地质综合影响系数,空旷平原地带该值取0.6[4]。

在考虑屏蔽因子的情况下,雷电直击线路次数计算如下。

式中,N为空旷地带架空线路受雷电直击次数,Ns为屏蔽作用下的直击次数,次/(100 km·年)。

考虑到由于树木吸引雷击而对线路造成感应过电压的情况,最终修正后的总闪络次数如下。

式中,N0为修正后的总闪络次数,N1为平原地形下的直击闪络次数,N2为平原地形下的感应闪络次数。Itr为树木吸引雷击引起线路感应闪络的最小雷电流幅值,kA；P(Itr)为树木吸引雷击引起线路感应闪络的概率。

2 雷电流幅值概率分布

1) 我国电力行业标准DL/T 620—1997推荐(国标推荐)的雷电流幅值概率分布函数如式(18)所示。

2) IEEE 1243—1997推荐的雷电流累积概率分布计算式如下。

式中,a的物理意义是中值电流,P(I0≥a)=0.5,b的物理意义是曲线陡度,代表了曲线下降的快慢。IEEE推荐取值为a=31、b=2.6。

3) 以IEEE 1243—1997的推荐模型为原型函数,基于广东某地市2018—2021年雷电定位系统的雷电数据,在Matlab软件中对该地市的雷电流数据进行拟合,得到的该线路的年平均雷电流累积概率如下。

上述国标推荐、IEEE推荐、该地市雷电流拟合公式的波形如图4所示,三者存在一定的差异。

图4 线路雷电流幅值概率分布

3 建弧率

绝缘闪络后要转化为稳定的工频电弧才会导致线路跳闸,国内配电网大部分采用中性点非有效接地方式,特点是一相闪络后相当于对其它相有耦合作用,因此其建弧率计算公式如下。

式中,Ue为线路额定电压,kV；lj为绝缘子爬电距离,m；lm为线路的线间距离,单位为m。

4 计算结果与分析

4.1 跳闸率计算结果

取雷击随机模拟次数为50000,可通过计算机得到雷击落点分布情况。结合电气几何模型,当雷击落点距线路的水平距离小于雷击大地的临界距离时,判断为直击雷,否则为感应雷,雷击大地的临界距离sk0的计算公式如下。

以广东省某地市山区的一条35 kV线路为例进行计算,该线路全长32 km,共98基杆塔,档距平均为200 m,孤垂平均为3.05 m,导线为LGJ 150钢芯铝绞线。该线路为无避雷线配置的单回架空线路,雷雨季节运行时曾多次出现雷击事件。根据地区监测数据拟合的雷电流幅值概率模型,经过50000次模拟后的绝缘子串闪络次数为3775,因此得出闪络率ξ=7.55 %。结合规程法计算配电线路耐雷水平[7],在不叠加工频电压、不考虑屏蔽因子的情况下,该线路的跳闸率为6.2879次/(100 km·年）。

考虑不同水平距离下、不同树木高度时击距的期望值,进而计算屏蔽因子的期望值,对雷击跳闸率进行修正,结果如图6所示。