铁路车轴微动磨损对微动裂纹扩展的影响研究
2024-04-23魏永刚
魏永刚


摘要:仿真计算了磨损/未磨损情况下不同深度微动裂纹尖端的等效应力强度因子ΔKeq,并从接触状态和应力分布两个角度阐述了影响机理。对于铁路车轴,考虑微动磨损时计算的ΔKeq更大,微动磨损促进了微动裂纹的扩展。当微动裂纹深度不大于2 mm时,磨损/未磨损情况下计算的ΔKeq相对误差大于7%。由于微动磨损,车轴轮座配合边缘及附近的区域出现了张开区,释放了过盈配合导致的压应力。此外,微动磨损在车轴轮座内部引入的应力集中增加了配合面下方的应力场。这两方面的共同作用促进了微动裂纹向车轴深度方向扩展。微动磨损对裂纹扩展的影响不能忽略,建议在车轴微动裂纹剩余寿命的评估中考虑微动磨损的影响。
关键词:铁路車轴;过盈配合;微动磨损;微动裂纹
中图分类号:TP204;U270.33 文献标志码:A doi:10.3969/j.issn.1006-0316.2024.02.005
文章编号:1006-0316 (2024) 02-0026-07
Investigation on the Effect of Fretting Wear on Fretting Crack Propagation of Railway Axles
WEI Yonggang
( College of Railway Locomotive, Jilin Railway Technology College, Jilin 132000, China )
Abstract:In this paper, the equivalent stress intensity factors ΔKeqof fretting crack tips at different crack depths in the case of worn/unworn were calculated. Thereafter, the influence mechanism was clarified from two perspectives of contact status and stress distribution. For railway axles, ΔKeqwas greater for the worn axles, which promoted the fretting crack propagation. When the crack depth was not greater than 2 mm, the relative error of ΔKeqcalculated under the worn/unworn condition was greater than 7%. Owing to fretting wear, an open zone appeared near the contact edge of the wheel seat, releasing the compressive stress induced by the interference fit. In addition, the stress concentration introduced by fretting wear increased the stress field below the contact surfaces. The combined effect of these two aspects promoted thefretting cracks propagation to the depth direction of the axle. The influence of fretting wear on crack propagation cannot be neglected, and it is recommended to take the influence of fretting wear in evaluating the remaining life of fretting cracks.
Key words:railway axle;interference fit;fretting wear;fretting crack
车轴是铁路列车的关键结构,其可靠性关系着行车安全。车轴与车轮经过盈配合方式连接,在循环旋转弯曲载荷作用下,轮轴配合边缘及附近区域会发生微动,这将导致该区域出现微动磨损损伤,并可能出现微动疲劳[1-3]。微动磨损会改变配合面的形貌,导致过盈配合部位的应力发生重分布,影响微动疲劳[4-5]。
铁路车轴的微动裂纹一般出现在距配合边缘几毫米的过盈配合内部[6]。由于结构的封闭性,小于2 mm的微动裂纹很难被准确检测[7-8]。一旦微动裂纹被错检或漏检将继续扩展,这可能导致车轴发生疲劳断裂,引发列车出轨等严重的安全事故。研究微动裂纹扩展对车轴检修间隔的制定和剩余寿命的预测非常重要。学者们针对过盈配合结构的微动裂纹扩展做了一些工作。Martínez[9]和Erena[10]等使用扩展有限元法(Extended Finite Element Method,XFEM)仿真研究了过盈配合结构的微动裂纹扩展,预测了裂纹扩展路径。Pourheidar等[11]基于Nasgro方程和循环R阻力曲线,评估了带初始缺陷的车轴过盈配合部位微动裂纹扩展寿命。然而上述研究没有考虑微动磨损的影响。微动磨损引起的配合部位应力重分布可能会影响微动裂纹扩展。Pinto等[12-13]针对圆柱-平面微动结构进行仿真,发现考虑微动磨损后预测的剩余寿命偏短。Madge等[14]指出微动磨损引起的应力变化会显著影响微动裂纹扩展。Zou等[15]测量实际车轴的微动磨损,并基于测量的轮廓进行仿真,发现微动磨损促进了车轴微动裂纹扩展,但没有详细阐明影响机理。综上,为保障铁路列车的安全运营,有必要系统研究车轴微动磨损对微动裂纹扩展的影响,并揭示影响机理。
本文基于Zou等[15]的实际车轴疲劳试验,在考虑微动磨损的情况下,仿真计算了不同长度微动裂纹对应的等效应力强度因子ΔKeq,并进行对比。之后,基于仿真结果,从接触状态和应力分布两个角度揭示了微动磨损对车轴微动裂纹扩展的影响机理。
1 车轴微动疲劳试验
1.1 试样与材料
实际车轴微动疲劳试验在Minden型轮轴疲劳试验台上进行。试验载荷F使用轮轴配合边缘的名义应力描述,为130 MPa。车轴旋转弯曲疲劳试验转速为1050 r/min。试验用车轴的形状尺寸如图1所示。车轴材料为EA4T车轴钢,车轮材料为ER8车轮钢,材料的机械性能参数如表1所示。
1.2 试验结果
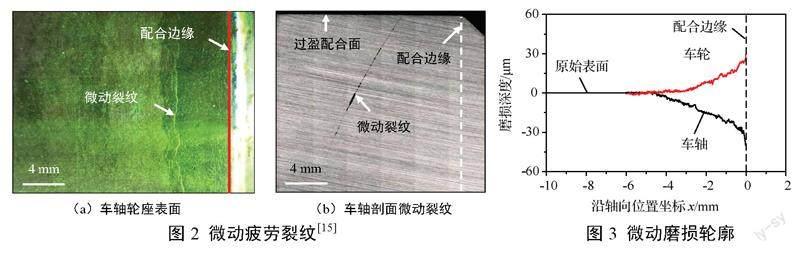
在4×107循环周次后,研究人员探测到明显的微动裂纹信号。此后停止试验,拆解车轮并对车轴轮座进行磁粉探伤。车轴轮座微动裂纹磁粉探伤结果如图2(a)所示,裂纹在车轴轮座表面沿圆周方向分布,距离车轴配合边缘约4.1 mm。微动裂纹在车轴剖面上的形貌如 图2(b)所示,裂纹与过盈配合面间存在一定角度,这说明微动裂纹受到多轴应力影响,以I-II混合型裂纹形式扩展。
研究人员还使用激光共聚焦显微镜对车轴和车轮的磨损情况进行了测量,得到了对应的磨损轮廓,如图3所示。可以看出,车轴和车轮的最大磨损深度都出现在配合边缘,分别为40 μm和29 μm。随着坐标位置向配合区内部移动,磨损深度逐渐减小。
2 有限元仿真
2.1 有限元模型
本文旨在对比研究微动磨损对车轴微动裂纹扩展的影响,因此分别建立磨损/未磨损车轴和车轮的有限元模型。具体建模过程为:首先,根据图1给出的试样形状尺寸,使用Hypermesh软件创建2D网格。由于配合边缘及附近的区域存在应力集中,对其网格进行细化,最小网格尺寸为50 μm。如图4所示,微动磨损的影响是通过在网格中引入磨损轮廓来实现。然后,通过绕对称轴旋转2D网格得到对应的3D网格。将该3D网格导入ABAQUS软件,即可得到仿真分析需要的有限元模型。
有限元模型由八节点六面体单元(C3D8)组成。车轴和车轮之间的接触面相互作用通过主从接触算法实现,其中车轮的内表面被定义为主面,车轴的轮座表面为从面。使用经典的库仑摩擦模型描述切向行为,摩擦系数设置为0.75。使用罚函数描述摩擦行为,最大弹性滑移容差设置为0.0001。根据车轴在试验台上的具体情况对有限元模型施加载荷和边界条件。如图4所示,车轮轮辋左侧表面x方向的位移被限制,车轮轮缘表面被固定。在第1个分析步中引入过盈配合,过盈量2Δ=0.243 mm。在第2个分析步时,在参考点F施加沿y轴的集中力Fy(Fy=F0,F0为施加的载荷值)。随后的分析步中,在参考点F分别施加两个随时间t变化的集中力Fy和Fz。通过这种车轴不动,载荷绕车轴旋转的方式,在轮轴配合边缘产生130 MPa的旋转弯曲应力。
2.2 微动疲劳裂纹建模
图2所示的微动裂纹在车轴轮座上沿圆周方向分布,这是过盈配合结构微动裂纹的典型特征。为便于仿真分析,以往的研究将这些裂纹简化为理想的环形裂纹[5,16]。本文使用交互积分法计算裂纹尖端的应力强度因子,微动裂纹同样被理想化为环形,如图5所示。裂纹尖端的渐近应力场存在奇异性,为准确对该奇异性进行表征,在紧邻裂纹尖端的位置创建了奇异性单元来计算应力强度因子。奇异性单元可以通过折叠常规高阶单元的单元边,并移动中间节点到单元边的1/4位置处构造得到。由于旋转弯曲应力,微动裂纹表面可能相互接触,从而产生裂纹闭合效应。为使裂纹面间的压应力得到有效传递,使用自接触算法模拟微动裂纹表面间的相互作用。摩擦系数设置为0.6[17],并使用“硬”接触来描述法向行为。裂纹前沿的积分路径数设置为15。
考虑到当前超声波探伤技术无法准确对小于2 mm的车轴微動裂纹进行探测,且不能使用应力强度因子描述短裂纹的扩展驱动力。因此,微动裂纹深度最小值设置为0.25 mm,最大为2 mm,裂纹扩展的增量设置为0.25 mm。
3 结果与讨论
3.1 应力强度因子
车轴受拉侧1 mm深度裂纹尖端的von Mises应力云图和不同积分路径上的应力强度因子如图6所示。可以看出,III型应力强度因子KIII几乎为零,这说明微动裂纹的扩展主要由I和II型应力强度因子KI和KII控制,为混合型裂纹。该仿真结果与图2(b)的试验现象吻合。此外,KI和KII在3~4个积分路径后趋于收敛。因此,本文使用积分路径编号为4~15上得到的KI和KII的均值进行计算。
式(3)的计算结果同样绘制在图7中。可以看出,相对误差随着裂纹扩展逐渐减小。这说明随着裂纹尖端远离过盈配合面,磨损对等效应力强度因子的影响逐渐减小。当裂纹深度为0.25 mm时,相对误差约40%;当裂纹深度为2 mm时,相对误差约7%。
超声波探伤技术无法准确检测到2 mm以内的微动裂纹。而仿真结果显示,当微动裂纹深度不大于2 mm时,磨损/未磨损情况下计算的等效应力强度因子的相对误差大于5%。如果在车轴微动裂纹剩余寿命的预测中忽略微动磨损的影响,将会高估车轴剩余寿命,导致危险的预测结果。为保障铁路列车的安全运营,建议在车轴微动裂纹剩余寿命的评估中,考虑微动磨损的影响。
3.2 影响机理分析
仿真结果显示,当微动裂纹深度小于2 mm时,磨损/未磨损情况下计算的等效应力强度因子存在明显区别。此外,微动裂纹深度越小,微动磨损的影响越大。本节以微动裂纹深度为0.25 mm的计算结果为例,分析微动磨损对裂纹扩展的影响机理。
3.2.1 接触状态的影响
仿真分析后车轴轮座的接触状态如图8所示。可以看出,不考虑磨损时,车轴轮座只有粘着区和滑移区。在微动磨损的作用下,配合边缘的材料被移除,形成图3所示微动磨损轮廓,车轴和车轮配合边缘过盈量减小。在旋转弯曲应力作用下,车轴和车轮发生分离,形成张开区。
仿真得到的车轴轮座受拉侧的接触压应力分布如图9所示。在不考虑微动磨损的情况下,车轴轮座配合边缘及附近区域处于滑移区,接触压应力的峰值出现在配合边缘。在微动磨损的作用下,配合边缘及附近区域的材料被移除,配合边缘附近区域出现张开区,此处的接触压应力为零。此外,由于微动磨损的作用,过盈配合内部出现磨损/未磨损边界,几何不连续导致新的接触压应力峰值出现在车轴轮座内部。
车轴轮座受拉侧的轴向应力S11分布如图10所示。由图9已知,在不考虑微动磨损的情况下,车轴轮座配合边缘及附近区域存在非常大的接触压应力,使车轮对车轴有很强的约束。即使在受拉侧,车轴轮座的轴向应力S11仍为负值。即是说,在不考虑微动磨损的情况下,车轴轮座的轴向应力始终为压应力,而在压应力作用下,裂纹闭合、不会扩展[19]。该仿真结果显然无法解释图2(b)中微动裂纹扩展的事实。当仿真考虑微动磨损影响后,车轴轮座配合边缘及附近区域出现张开区,张开区内轮轴间的压应力被释放,轴向应力S11由负变正,这促进了裂纹向车轴深度方向的扩展。
由图8~10可知,在微动磨损的作用下,车轴轮座配合边缘及附近的材料被移除,过盈量减小。在外部疲劳载荷作用下,配合边缘及附近出现张开区,车轮和车轴间的压应力被释放,导致磨损时计算的等效应力强度因子更大。
3.2.2 应力集中的影响
微动磨损会导致过盈配合内部出现磨损/未磨损边界,从而引发应力集中。配合面上的应力集中也可能影响配合面下方的应力分布。车轴轮座过盈配合面下方的von Mises应力云图如图11所示。可以看出,在不考虑微动磨损的情况下,车轴过盈配合面的应力集中出现在配合边缘,距微动裂纹位置较远,不会影响微动裂纹扩展。当考虑磨损的影响后,过盈配合面的应力集中出现在磨损/未磨损边界附近,靠近微动疲劳裂纹,此时,过盈配合面上由微动磨损引发的应力集中影响了裂纹尖端附近的应力场,这导致磨损情况下计算的等效应力强度因子更大。
综上,微动磨损从两个方面影响车轴微动裂纹扩展。一方面,微动磨损导致车轴轮座配合边缘及附近的材料被移除,过盈量减小。在旋转弯曲应力作用下,车轴和车轮配合面发生分离,出现张开区。张开区的出现释放了过盈配合的压应力,促进了微动裂纹扩展。另一方面,微动磨损在车轴轮座内部微动裂纹附近(磨损/未磨损边界)引入新的应力集中,这会增加配合面下方裂纹尖端的应力场,同样会促进微动裂纹扩展。越靠近过盈配合面,由微动磨损导致的压应力释放,以及微动磨损导致应力集中的影响越显著。随着裂纹尖端远离配合面,这些影响会逐渐变小,从而导致出现图7中随着裂纹深度增加,相对误差减小的仿真结果。
4 结论
本文基于实际车轴微动疲劳试验结果,仿真计算了磨损/未磨损情况下,不同深度微动裂纹尖端的等效应力强度因子,并进行对比。此后,基于仿真结果,从接触状态和应力分布两个角度阐述了微动磨损对微动裂纹扩展的影响机理。主要结论如下:
(1)对于铁路车轴,考虑微动磨损情况下计算的等效应力强度因子更大,这说明微动磨损会促进微动裂纹的扩展。当微动裂纹深度不大于2 mm时,磨损/未磨损情况下计算的等效应力强度因子相对误差大于7%,铁路车轴微动磨损对微动裂纹扩展的影响不能忽略。
(2)由于微動磨损,车轴轮座配合边缘及附近出现了张开区,释放了过盈配合引入的压应力。此外,微动磨损在车轴轮座内部引入的应力集中增加了过盈配合面下方的应力场。这两方面的共同作用促进了微动裂纹向铁路车轴深度方向扩展。
(3)为保障铁路列车的安全运营,建议在车轴微动裂纹剩余寿命的评估中,考虑微动磨损的影响。
参考文献:
[1]MAKINO T,SAKAI H,KOZUKA C,et al. Overview of fatigue damage evaluation rule for railway axles in Japan and fatigue property of railway axle made of medium carbon steel[J]. International Journal of Fatigue,2020(132):105361.
[2]FOLETTI S,BERETTA S,GURER G. Defect acceptability under full-scale fretting fatigue tests for railway axles[J]. International Journal of Fatigue,2016(86):34-43.
[3]王大強. DF21型米轨机车车轴轮座裂纹分析及解决措施[J]. 科技研究,2014(3):21-22
[4]LEE D-H,KWON S-J,YOU W-H,et al. Numerical analysis of the effect of contact pressure on the fretting fatigue life in a press-fitted shaft[J]. Journal of the Korean Physical Society,2009,54(3):1115-1118.
[5]ZHANG Y B,LU L T,GONG Y B,et al. Fretting wear-induced evolution of surface damage in press-fitted shaft[J]. Wear,2017(384):131-141.
[6]CERVELLO S. Fatigue properties of railway axles:New results of full-scale specimens from Euraxles project[J]. International Journal of Fatigue,2016(86):2-12.
[7]ZERBST U,KLINGER C,KLINGBEIL D. Structural assessment of railway axles A critical review[J]. Engineering Failure Analysis,2013(35):54-65.
[8]ZERBST U,BERETTA S,K?HLER G,et al. Safe life and damage tolerance aspects of railway axles A review[J]. Engineering Fracture Mechanics,2013(98):214-271.
[9]MART?NEZ J C,VANEGAS USECHEL V,WAHAB M A. Numerical prediction of fretting fatigue crack trajectory in a railway axle using XFEM[J]. International Journal of Fatigue,2017(100):32-49.
[10]ERENA D,V?ZQUEZ J,NAVARRO C,et al. Numerical study on the influence of artificial internal stress relief groove on fretting fatigue in a shrink-fitted assembly[J]. Tribology International,2020(151):106443.
[11]POURHEIDAR A,REGAZZI D,CERVELLO S,et al. Fretting fatigue analysis of full-scale railway axles in presence of artificial micro-notches[J]. Tribology International,2020(150):106383.
[12]PINTO A L,TALEMI R,ARA?JO J A. Fretting fatigue total life assessment including wear and a varying critical distance[J]. International Journal of Fatigue,2022(156):106589.
[13]PINTO A L,ARA?JO J,TALEMI R. Effects of fretting wear process on fatigue crack propagation and life assessment[J]. Tribology International,2021(156):106787.
[14]MADGE J J,LEEN S B,SHIPWAY P H. A combined wear and crack nucleation propagation methodology for fretting fatigue prediction[J]. International Journal of Fatigue,2008,30(9):1509-1528.
[15]ZOU L,ZENG D,LI Y,et al. Experimental and numerical study on fretting wear and fatigue of full-scale railway axles[J]. Railway Engineering Science,2020,28(4):365-381.
[16]G?RER G,G?R C H. Failure analysis of fretting fatigue initiation and growth on railway axle press-fits[J]. Engineering Failure Analysis,2017(84):151-166
[17]WU S C,XU Z W,LIU Y X,et al. On the residual life assessment of high-speed railway axles due to induction hardening[J]. International Journal of Rail Transportation,2018,6(4):218-232.
[18]IRWIN G R. Fracture mechanics,in the book of structural mechanics[M]. New York, USA:Pergamon Press,1958:55794.
[19]KUBOTA M,KATAOKA S, KONDO Y. Effect of stress relief groove on fretting fatigue strength and index for the selection of optimal groove shape[J]. International Journal of Fatigue,2009,31(3):439-446.
