粘弹性圆柱绕流场的稀疏化动态模态分解方法

李 璇，苏 进

(西安工程大学 理学院，陕西 西安 710048)

0 引言

粘弹性流体是一种具有粘性和弹性的特殊非时变性非牛顿流体，在生物工程等多种领域有着广泛应用。针对粘弹性圆柱绕流问题，不仅要考虑圆柱壁面(边界)的流动特点，还需考虑粘弹性圆柱绕流所具有的减阻特性。因而，分析弹性诱导的涡团结构特征对粘弹性流体的工程应用具有重要价值[1-2]。近年来，学者们对流体流动结构进行了较多研究：Thomases等[3]针对四辊轧机几何中的粘弹性流体，利用本征正交分解(proper orthogonal decomposition，POD)提取了弹性模态，并根据其能量贡献分析了流体动力学特征；Henshaw等[4]采用POD量化流体动力学系统的模型结构；Shakeri等[5]利用POD提取了聚合物的弹性湍流结构并发现反向旋转涡对流动的总动能有显著贡献。最近在流体动力学领域内，动态模态分解[6](dynamic mode decomposition，DMD)广泛用于分析非定常流场[7]的流动特征和构建低阶的流场动力学模型[8-9]。与POD形成的完全基于空间相关性和能量含量的模态层次结构相比，DMD方法分解后的每个模态由空间的相关结构组成，在时间上具有相同的线性行为[10]。DMD可以看作是将奇异值分解(singular value decomposition，SVD)在空间降维方面的优点与快速傅里叶变换(fast fourier transform，FFT)在时间频率识别方面的优点相结合。然而，在高速绕流条件下，粘弹性圆柱绕流场流体粘性减小阻力较低，随着速度的增加减阻效果逐渐减弱，这导致粘弹性圆柱绕流流场结构中有很多复杂的模态特征。DMD虽然在牛顿流体流场数据降维方面起到了一定的作用[11-12]，但是对于粘弹性圆柱绕流数据的减阻现象往往不能起到很好的降维效果。

针对粘弹性圆柱绕流问题，为实现粘弹流高效的结构分析和动态预测，引入一种基于稀疏促进优化的DMD方法(SP-DMD)，与传统的DMD相比，该方法可以剔除粘弹性流体中的非关键模态。在粘弹性流场演化中，SP-DMD使粘弹性流场中关键模态的数量和降维近似残差之间处于平衡状态，从而更利于分析和发现那些能够对粘弹性圆柱绕流场发展起关键性作用的因素。此外，当模态数量增加时，SP-DMD重构的流场可以得到更多的局部流动细节，并且与原始流场进行对比，局部较小尺度的涡团形态以及空间分布的特点都能够很好地重现出来。

1 DMD算法

从数学角度看，DMD是对Koopman算子模态的近似，从谐波的角度反映流场的特性。DMD方法的运用需要从数值模拟或物理实验中收集一系列快照x1，x2，...，xm+1，并形成一个数据矩阵：

(x1x2...xm+1)。

其中矩阵的每一列表示每一时刻的空间状态。此外，假定数据在时间上是等距采样的，时间步长为Δt。通常情况下，每一个快照xi=x(iΔt)是一个有n分量的复向量，即xi∈n。

从快照序列中构造两个快照矩阵：

其中，X∈n×m，X′∈n×m。并假设快照是由离散时间线性时变系统生成的，该系统表示如下：

xk+1=Axk，k=1，2，...，m。

线性算子A记录着快照序列的动态特性。在粘弹性流体问题中，矩阵A中包含大量数据，且一般情况下为复数。每个快照xi中分量的数量通常远大于快照的数量，即n>>m。

根据两个连续时间步长之间的线性关系xk+1=Axk，k=1，2，...，m，将数据矩阵X和X′通过线性算子A连接起来，则矩阵X′有如下表示：

因此，求出线性算子A是DMD的主要目标。

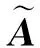
(1)对矩阵X∈n×m进行奇异值分解(SVD)：

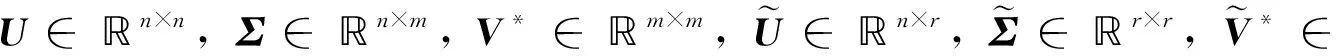
假设数据总维数是m，上述SVD通过选择适当的截断值r来减少数据矩阵的维数，被消除的冗余项就用rem(redundancy term)表示，其维数是m-r。

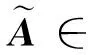
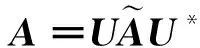
其中，矩阵Q的Frobenius范数由下式来决定：

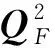
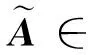
(1)

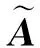
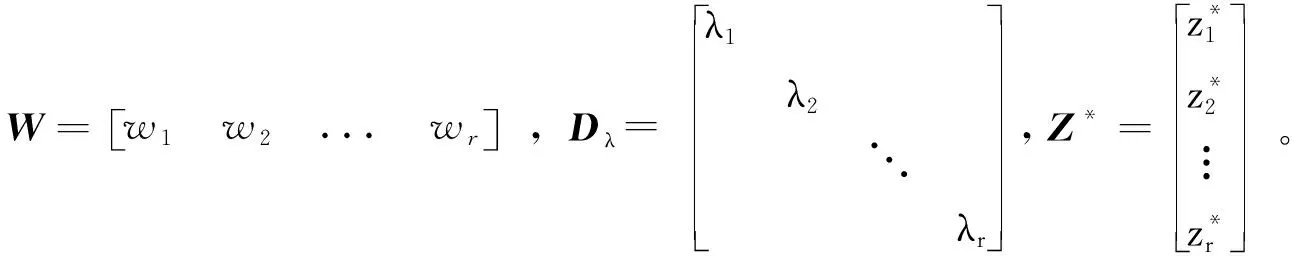
动力学方程(1)所生成的每一组数据为：

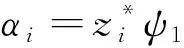
且每个αi是对应DMD模态的振幅。同样，在矩阵形式中有：

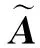
则有

X≈ΦDαVand。

(2)

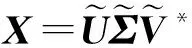
(3)

J(α)可以等价表示为：

J(α)=α*pα-q*α-α*q+s，

(4)

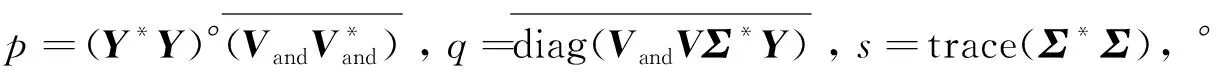
(7)通过最小化关于α的二次函数(4)可以得到该优化问题(3)的DMD振幅的最优矢量为：

2 稀疏化动态模态分解(SP-DMD)方法

DMD算法虽然能够求出振幅最优向量和提取出关键模态，但由于在维数较高的粘弹流中还存在部分非关键模态未剔除，因此引入稀疏化动态模态分解(SP-DMD)方法来剔除这些非关键模态。

2.1 SP-DMD核心思想

SP-DMD需要在所有DMD模态中提取出若干关键的具有非零幅值的模态，然后通过算法来调整其幅值，具体方法如下：

具有非零幅值的DMD模态可以通过求解如下凸优化问题而得到：

minJ(α)，
s.t.ETα=0。

(5)

式(5)中，矩阵E反映了振幅向量的稀疏结构信息。E的列均是单位向量，其非零元素对应于具有零幅值的DMD模态。获得具有非零幅值的DMD模态后，通过改变其幅值实现降维近似。

将优化问题(3)进行修改，通过给式(3)中的目标函数J(α)增加一个正则化项card(α)来解决稀疏性的问题，这就惩罚了未知振幅向量Dα中非零元素的数量：

(6)

在修改后的优化问题(6)中，γ是正则化参数，它反映了“稀疏化”振幅向量Dα的权重性。γ越大，说明越重视向量Dα中非零元素的数量。因此，鼓励用(6)这个更稀疏的解决方案。

一般来说，找到问题(6)的解决方案相当于组合搜索，对于任何问题，组合搜索会变得很棘手。为了绕过这个问题，引入问题(6)的更宽泛的表述，通过用向量Dα的L1范数来代替基函数：

(7)

SP-DMD的核心思想就是找到式(7)的解，这是一个凸优化问题，解决该问题使用了交替方向乘子法(alternating direction method of multipliers，ADMM)，在实验或数值快照降维近似质量和DMD模态数量之间达到预期的平衡后，从而确定最终优化后的稀疏化振幅向量Dα。

2.2 交替方向乘子法

交替方向乘子法(ADMM)是一种用于求解优化问题的计算框架，适用于求解分布式凸优化问题。ADMM算法将大的全局问题分解为多个较小且较容易求解的局部子问题，并通过协调子问题的解而得到大的全局问题的解。ADMM通常用于求解两个优化变量且只含等式约束条件的优化问题，其一般表示形式为：

minf(x)+g(z)，

s.t.Ax+Bz=c。

其中，x和z是优化变量，f(·)和g(·)都是凸函数。

引入增广拉格朗日函数：

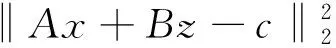
其中：λ为拉格朗日乘子；ρ为惩罚系数且ρ>0。

由于ADMM算法是基于增广拉格朗日函数最小化的迭代算法，迭代方式如下所示：

λk+1=λk+ρ(Axk+1+Bzk+1-c)。

从初始点开始进行迭代，直到满足如下优化条件和停止准则：

Axk+1+Bzk+1-c2≤εprim，

zk+1-zk+12≤εdual。

其中，εprim，εdual表示停止准则的阈值。

3 数值算例

3.1 粘弹性圆柱绕流模型参数设置

为了模拟粘弹性圆柱绕流在高Re数下的湍流减阻现象，设置流场中的平均流速为U，圆柱直径的特征长度尺寸为d，几何特征停留时间为d/U。流体弹性特征的参数为Wi=λU/d，表征流体黏性特征的参数为Re=ρUd/η。

选取如图1所示的几何示意图进行二维粘弹性圆柱绕流湍流减阻的模拟。

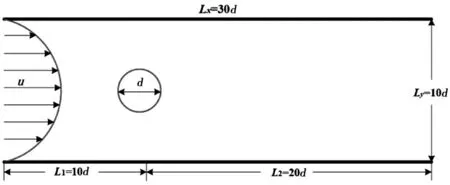
图1 粘弹性圆柱绕流的几何模型

采用双分布 LBM-IBM 耦合算法模拟粘弹圆柱绕流，设置Re=1000，粘度比β=ηs/η=0.01。数值模拟参数如表1所示。

表1 数值模拟参数

宏观方程的处理采用IBM耦合D2Q9格子模型，D2Q9格子模型中碰撞迁移过程的边界处理为非平衡外推格式，区域上下边界采用无滑移条件，即

出口处按充分发展条件处理，出口处的水平速度的法向导数为0，其中n是单位法向量，即

这里入口处的初始水平速度u设置成抛物状，初始垂直速度v=0，入口的初始速度

u(0，y)=3Umaxy(10-y)/50，

其中，Umax是通道水平中线处的最大速度且U=2Umax/3。

对于本构方程采用Oldroyd-B方程的格子Boltzmann模型，应力张量的分布函数上下壁面的边界条件应用非平衡态外推方法，计算区域的上下边界的应力分量为

τyy=0。

入口和出口边界的应力分量采用充分发展边界条件，即

3.2 粘弹性圆柱绕流数值结果

不同的Re(Reynolds)数对应的Wi(Weissenberg)不同，且Wi是Re的函数。根据3.1节所述，模拟出Re=1000时的粘弹性圆柱绕流流场的数据，并且对流体弹性特征数Wi=1的数据进行研究。每一时刻的流场数据构成一个301×601的网格。

在研究粘弹性圆柱绕流问题的过程中，首先要将二维数据转化成一维，由此可知每一时刻所对应的空间维数高达180 901维。由于各种运动形态和不同结构的尾流流态会表现出不同的能量和频率，仅通过对瞬态流场的观察，很难对粘弹性圆柱绕流流场的特性进行深入理解。因此研究过程中，选择了连续1 000个时刻的二维粘弹性流场数据进行DMD算法处理，可以得到302个模态。得到的302个DMD模态的特征值在复数坐标系内的分布情况如图2所示，这些特征值进行对数化后的分布情况如图3所示。

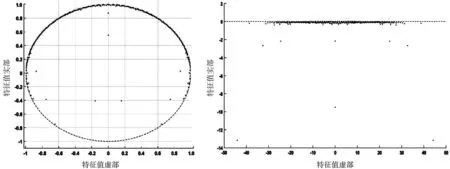
图2 DMD未对数化的特征值分布 图3 DMD对数化的特征值分布

由图2可知，大部分的DMD模态捕捉到的流场结构强度近似处于稳定的状态。此外，还可以发现有个别特征值落在单位圆内部，并且距离单位圆较远，此现象表示这部分特征值所对应的流场结构强度的衰减率比较大，流场结构的状态不稳定，将在随后的圆柱绕流流场演化过程中逐渐消散。由图3可知，每个特征值的实部(即衰减率)都基本接近于0，这更直观地表明了大部分DMD模态所对应的流场结构强度是近似稳定的。

采用SP-DMD和标准DMD算法得到的粘弹性流场非对数化特征值的对比如图4(a)所示。由于该图不能清晰地看出特征值的分布情况，将其局部放大，如图4(b)所示。

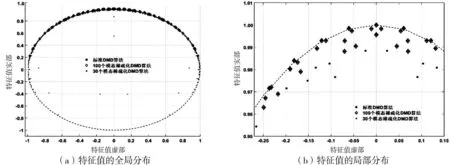
图4 DMD和SP-DMD未对数化的特征值分布

在采用SP-DMD时，分别保留了30个模态和100个模态进行对比。SP-DMD关注的是DMD模态在整个粘弹性圆柱绕流流场的演化过程中对流场的贡献，通过SP-DMD能够更加方便地识别并提取在整个流场的演化过程中起到比较重要影响作用的模态信息。由图4可知，利用标准DMD算法所得到的具有较大衰减率的模态在SP-DMD中都被有效剔除了，从而保留了有稳定状态的DMD模态。

幅值与频率之间的关系可以定义为DMD频谱，在研究粘弹性流场问题的过程中，DMD频谱能够将流场结构所包含的能量情况反映出来，因此又将其称之为能谱。采用两种方法所获得的模态幅值与特征值虚部(频率)的关系如图5所示，对其进行局部放大如图6所示。利用两种方法所得到的模态幅值与特值实部(衰减率)的关系如图7所示，其局部放大如图8所示。

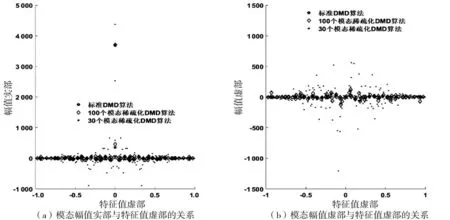
图5 采用 DMD 与 SP-DMD 得到的模态幅值与特征值虚部(频率)的关系

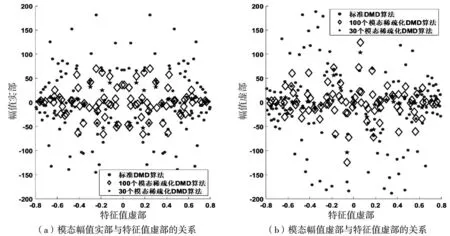
图6 采用 DMD 与 SP-DMD 得到的模态幅值与特征值虚部(频率)的关系的局部放大

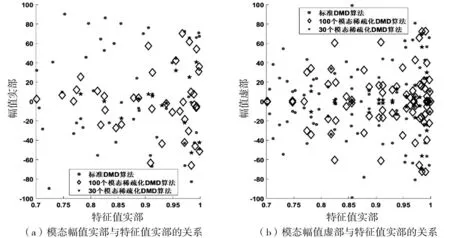
图8 采用 DMD 与 SP-DMD 得到的模态幅值与特征值实部(衰减率)的关系的局部放大

由图5、6、7、8可知，部分具有较大衰减率的非稳定的DMD模态所对应的流场结构承载着较多的能量，其对流场初期演化的影响较强，但在后期的演化过程中，影响力明显下降。SP-DMD将能够最大程度反映流场信息的稳定模态保留下来，并对保留的模态幅值进行调整，从而达到对原始粘弹性流场降维的效果。

利用SP-DMD所获得的100个模态与30个模态对流场进行重构后的粘弹性圆柱绕流流场结构的空间分布如图9(c)和图9(d)所示。为了验证SP-DMD有着较好的优化降维效果，采用标准DMD所获得的302个模态对流场进行重构后的粘弹性圆柱绕流流场结构的空间分布如图9(b)所示。为了进行比较，原始的瞬态流场如图9(a)所示。

图9 原始流场与DMD和SP-DND重构流场的对比

由图9可知，用30个模态对圆柱绕流流场进行重构就可以将原始流场的整体流动形态重现，并且能够较好地刻画出局部较大尺度的流场结构。当模态的数量增加到100时，可以看到重构流场中显示出更多的局部细节。然而，标准DMD算法由302个模态才能较好地刻画出原始流场的整体形态。由此可见，SP-DMD能够对将流场的非关键信息进行剔除，从而保留并提取具有稳定状态的关键流场结构。

4 结论

针对粘弹性圆柱绕流涡团结构的研究，引入了DMD与稀疏促进相结合的特征分析方法。该方法在提取粘弹性流场关键模态时，不只考虑幅值，而且通过计算模态对流场贡献率来剔除非关键模态，从而留下产生影响较大的关键模态，使重构后的粘弹性流场仍然可以保留原始粘弹流流场中的重要动态信息。因此，利用SP-DMD可以更好地解析粘弹性圆柱绕流流场的特性，为粘弹性圆柱绕流流场的特性分析研究提供了新的视角。在未来的发展中，能否将包含控制输入的模型预测控制与SP-DMD相结合来解决实际问题，还有待进一步测试和改进。