B样条驱动纹理生成的构造式信息隐藏

郦姝伊，韩彦芳，乐燕芬，姚恒，秦川

上海理工大学光电信息与计算机工程学院，上海 200093

0 引言

信息隐藏是信息安全的一个重要领域，包含隐蔽信道和多媒体信息隐藏两种技术，而多媒体信息隐藏技术（Johnson 和Jajodia，1998）是一种将秘密信息隐藏于公开载体中，在实现收发双方秘密通信的同时不被觉察的技术。一般来说，信息隐藏使用的载体多为有意义的数字载体，如数字图像（欧博 等，2022；武晓帅 等，2022；周航 等，2022）、文字、音频、视频和3D 模型（Wang 等，2019）等，其中数字图像在工作、学习和生活等各个领域的广泛应用催生出越来越多的基于数字图像的信息隐藏算法（Liu 等，2019；Yi 等，2018；Qin 等，2018）。传统的以最低有效位（least significant bit，LSB）（Wang和Wang，2004）和JSteg（JPEG steganography）（Fridrich 和Goljan，2002）为代表的基于修改载体的信息隐藏算法，利用载体图像的冗余隐藏信息。随后，学者们又提出了将信息隐藏与编码相结合的编码隐写算法，如湿纸码（Fridrich 等，2005）、F5 算法（Westfeld，2001）和ZZW算法（Zhang等，2008）等。

随着信息隐藏技术的不断发展，隐写分析技术也日趋完善，传统的通过改变载体的信息隐藏算法面临着检测危机。因此，有学者提出了无载体信息隐藏技术（Zhou 等，2015）。“无载体”并非无需传输媒介，而是指通过秘密信息驱动以选择或构造的方式获取含密载体（周志立 等，2016）。基于图像选择的无载体信息隐藏算法通常利用图像的亮度、颜色、纹理、边缘和轮廓等特征信息，建立特征与秘密信息之间的映射，通过秘密信息与图像特征的对应选择合适的载体图像进行传输。现有的方案基于尺度不变特征变换（scale-invariant feature transform，SIFT）（董腾林 等，2021）、DCT（discrete cosine transform）特征提取（Zhang 等，2018）和高维深度特征（Zou 等，2022）等。其中，董腾林等人（2021）利用图像SIFT特征映射为哈希值，通过对比秘密信息片段与所有的图像哈希值选择载体图像实现信息隐藏；Zhang等人（2018）用LDA（linear discriminant analysis）模型将图像库分类，根据图像DCT 变换生成特征序列并构建倒排索引，选择同一类别中秘密信息对应的索引图像作为含密载体；Zou 等人（2022）构造图像深度哈希值与秘密信息段的映射，且收发双方利用相同的无监督聚类方法构造相同无载体图像集（coverless image dataset，CID），通过传输CID 中与秘密信息对应的图像实现信息隐藏。

基于图像构造的无载体信息隐藏算法则是以秘密信息为驱动直接生成含密图像。纹理生成技术的日益成熟为研究者们提供了一个新思路。Otori 和Kuriyama（2007，2009）提出在纹理图像的生成过程中隐藏信息，这类算法利用局部二值模式（local binary pattern，LBP）建立二进制数据与颜色或纹理的映射关系，根据秘密信息从参考纹理图像中选择对应的颜色或纹理块进行拼接，从而构造出一幅较大的含密纹理图像。然而，这类基于纹理的构造式信息隐藏技术仍存在一些缺陷，如需要现存的纹理图像作参考、生成图像尺寸较大、抗JPEG 压缩能力差以及抗隐写分析能力差等。后有研究者提出利用数学方法而非模拟已有纹理图像的构造方案。Qian等人（2018b）通过建立一个与二进制数据相映射的图形库，根据秘密信息选择相应的图形并进行放缩和旋转操作，将它们不重叠地散布于简易轮廓内部，以构造含密纹理图像。Qian 等人（2018a）通过秘密信息改变初始图案角点位置，为图像填充颜色并进行模拟水影画的形变操作构造含密纹理图像。但Qian 等人（2018a，b）算法需要已有的轮廓图案作为生成图像的约束，若不人工增加轮廓图案种类则生成含密图像的样式单一。Xu 等人（2015）通过生成大理石纹理图像隐藏信息，该算法直接将秘密信息绘制于空白画布上，在不含信息的空白部分填充背景图案，利用模拟大理石花纹的形变算法生成具有复杂纹理结构的数字图像。潘琳等人（2016）结合大理石纹理生成算法，建立二进制数据与图形映射库，从图形库中选择与秘密信息对应的图形散布于空白画布中，经过填充背景和模拟大理石纹理的形变操作生成复杂的含密纹理图像。司广文等人（2020）采用空间金字塔算法提取纹理图像特征，并通过监督分类训练得到分类模型，构造图像特征与二进制数据的映射字典隐藏信息，利用形变函数生成纹理图像。但上述3 篇文献提出的纹理构造算法均为通过图像内容的坐标位置或图案等空域特征隐藏秘密信息，含密图案及坐标可通过对图像内容进行图案匹配或角点检测直接获取，故当共享图案库被破解时，秘密信息将很容易直接从图像中提取出来，导致此类传统的构造式信息隐藏算法的安全性遭到威胁。

经调研发现，B 样条曲线已在计算机辅助设计和计算机图形学中得到了广泛的应用。由于其具有空间唯一性、有界性、连续性、局部形状控制能力和仿射变换不变性等强大性能，可将其应用于信息隐藏领域。现已有研究者利用B 样条解决图像配准（Sun等，2017）和指纹认证（Gou 和Wu，2005）等技术上的问题。因此，本文利用B 样条的曲线绘制功能和其有界性、局部形状控制能力及仿射不变性等属性，提出一种新的构造式信息隐藏算法。

本文工作的主要贡献如下：1）提出一种利用B样条驱动含密纹理图像生成的构造式信息隐藏算法。以B 样条曲线的控制点作为特征，在利用控制点绘制纹理图像的过程中，将秘密信息间接地隐藏在生成图像的空域中。2）通过构建数组在颜色库中的映射规则，将用于提取图像中秘密信息的密钥以填充颜色的方式隐藏在含密图像中。3）本构造式信息隐藏算法的隐藏容量较灵活，且相较于已有的传统构造式信息隐藏算法，本文算法可抵抗的图像攻击种类更多且鲁棒性更强，并具有一定的抗隐写分析能力。

1 本文算法

本文提出的B 样条驱动纹理生成的构造式信息隐藏算法大致分为含密图像构造和秘密信息提取两个阶段，秘密信息的收发双方需共享相同颜色库，且在纹理曲线绘制过程中用于加密操作的密钥以隐蔽的方式在收发双方间传输。算法框架如图1所示。

图1 本文算法框架Fig.1 Framework of the proposed algorithm

在含密图像构造阶段，发送方首先将画布分块、编号并利用密钥置乱，然后随机选取一组图像子块，并用直线拟合它们的中点，将拟合直线与画布边缘的交点和所选子块的中点共同作为初始B 样条控制点，由此确定待生成图像中纹理曲线的形状和走向。之后将拟合直线多次等间隔平移后作为定位直线，并将初始控制点经仿射变换操作移至各定位直线位置，依次绘制B 样条曲线即获得多条未隐藏信息的参考曲线。再根据秘密信息调整各参考曲线控制点的数量及位置，生成含密纹理图像。最后利用本文提出的数组在颜色库中的映射规则，将随机选取的子块编号以填充颜色的方式隐藏在图像中，即完成了含密纹理图像的构造。

在信息提取阶段，接收方首先利用接收到的密钥对含密纹理图像进行与发送方相同的分块、编号及置乱操作，并通过数组在颜色库中的映射规则获取初始B 样条控制点。然后，提取纹理图像中的含密曲线并结合初始控制点生成参考曲线。最后，结合参考曲线求解出含密曲线的控制点，进而通过与参考曲线的控制点对比提取出秘密信息。

1.1 生成参考纹理曲线

发送方首先将空白画布分为互不重叠的子块并编号，为提高安全性，利用密钥对子块编号进行置乱加密，具体为

式中，X为原始编号，X′为置乱后编号，Q为分块总数，w是一个素数密钥且有w∈[1，Q]。随机选取2d(d∈N)个1～Q内的子块编号，并拟合这些编号的子块中点获得拟合直线l，l与画布边缘的交点分别为(ax，ay)和(bx，by)，所选图像子块中点和它们的拟合直线如图2（a）中的圆圈和斜线所示。将子块中点及点(ax，ay)和(bx，by)以从左至右方向排序，即获得一组初始控制点C=，其中c0==(bx，by)。根据初始控制点集C绘制的B样条曲线如图2（b）所示。

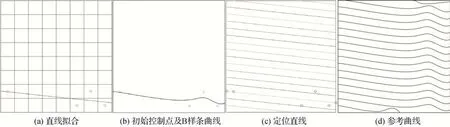
图2 生成参考条纹Fig.2 The generation of reference stripes（（a）linear fitting；（b）initial control points and initial B-spline curve；（c）position line；（d）reference curve）

B样条曲线可写为S(t)=(Sx(t)，Sy(t))，其中t为连续的非递减参数索引序列，它的B 样条逼近函数为

式中，ci=(ci，x，ci，y)(i=0，1，…，n)表示第i+1 个控制顶点，Bi，k(t)(i=0，1，…，n)称为k次B 样条的基函数。Bi，k的递归计算为

式中，Bi，k的双下标中第1下标i表示序号，第2下标k表示次数，T={t0，t1，…，tn+k+1}为节点矢量，表示B样条各段的连接点，这些节点与曲线的型值点一一对应，节点位置的改变将影响B样条曲线的形状，同时也会导致控制点位置的改变。

为生成互不重叠的纹理曲线，现将直线l在画布中沿其法线方向进行等间隔平移，记直线l经第j次平移后所获得的直线为lj，其与画布边缘的两交点分别为(aj，x，aj，y)和(bj，x，bj，y)。将直线l平移m次，即获得定位直线集L={l1，l2，…，lm}，如图2（c）中的直线所示。

最后对控制点集C进行多次仿射变换，使c0和分别移到位置lj(j=1，…，m)的(aj，x，aj，y)和(bj，x，bj，y)处，即获得控制点集Cr=，其中任一组控制点(j=1，…，m)。分别绘制B样条曲线，即获得均匀分布于画布中的不含有秘密信息的参考曲线集Sr=，将由参考曲线构成的纹理图像称为均匀纹理图像，如图2（d）所示。特别地，当随机选取子块数2d=2，即初始控制点数为4 时，生成的参考曲线为直线。

1.2 信息隐藏

由于各参考曲线的长度与它们所对应的定位直线的长度成正相关，因此将根据各定位直线的长度自适应地决定各待隐藏信息的参考曲线中的隐藏容量。预设密集参数N（N＞1），将定位直线集L中的任意定位直线lj的长度记为rj，则其中可隐藏的秘密信息比特数qj=[rj/N]，其中[·]为取整运算符。故选取参数N的值越小，该曲线的隐藏容量越小，对曲线的扰动越小，进而生成的曲线越平滑，反之则隐藏容量越大，生成的曲线越抖动。若qj≤min(k，2d)，则令qj=min(k，2d)，并将此参考曲线标记为不可隐藏曲线，否则将此参考曲线标记为待隐藏曲线。由所有构造各参考曲线的信息隐藏容量集合Q={qj}(j=1，2，…，m)。在对B 样条曲线进行信息隐藏的过程中，需通过插入节点增多用于隐藏信息的控制点数量。

对于k次B 样条曲线S[B](t)，其B 样条基由节点矢量T=[t0，t1，…，tn+k+1]完全决定。此时插入节点t∈[ti，ti+1]⊂[tk，tn+1]，得到新的节点矢量T1=[t0，t1，…，ti，t，ti+1，…，tn+k+1]，重新编号为T1=，此新的节点矢量T1决定了一组新的B样条基。原B 样条曲线即可用新的样条基及新控制顶点表示，计算为

控制顶点增加一个，但曲线形状及连续性均保持不变。插入一个非重节点时，新的控制顶点可由节点插入算法获得，计算过程为

式中，αj=，插入节点后所得的新B样条控制点与原控制点都定义同一条B 样条曲线。对各参考曲线均进行相同操作，以第i条参考曲线为例，生成含密曲线的步骤如下：

图3 信息隐藏及含密图像的生成Fig.3 Information hiding and stego image generation（（a）stego curve generation；（b）stego texture image）

2）根据秘密信息移动控制点位置，在隐藏信息的同时改变曲线的局部形状。对控制点，当隐藏信息为1时，将该点沿控制点连线的法线方向移动h距离，其中h为预设的移动距离，当隐藏信息为0 时则不改变控制点位置。为保证生成的含密曲线不相互重叠，距离h应取小于定位直线间距的一半。对于不隐藏信息的参考曲线，通过随机二进制数组随机改变控制点位置，使含密与不含密图像具有类似的平滑度。图3（a）中三角形即为隐藏信息后的控制点。

1.3 含密纹理图像生成

本文提出一种数组在颜色库中的映射规则，将用于获取初始控制点的编号以颜色填充的方式隐藏在图像中。

将空白画布均匀分割为2M×2M个互不重叠子块的空白画布，各子块编号可由2×M比特二进制数表示，故2d个块编号的二进制形式可由M×2d+1比特表示。现将此M×2d+1比特序列分为2d+1段，每段含M比特，按各段在原序列中的顺序，将它们从0～2d+1-1 进行编号，各编号可用d+1比特表示。将各M比特段与某对应的d+1 比特的段号进行组合，构建新的二进制表示。故所构造颜色库中需含有2M+d+1种颜色，每种颜色可用唯一的M+d+1 比特表示，实现2d个块编号与颜色库中颜色序号的唯一映射。

如图4 所示，令M=3，d=1，即将一幅图像划分为64 个块，随机选取2 个子块。设随机选取并排序后的块编号为［8，17］，它们的二进制表示为［001000，010001］，并以3 bits为单位进行分段，获得［001，000，010，001］，在各分段后加入它们的二进制序号可表示为［00100，00001，01010，00111］，对应编号为4、1、10、7 的颜色，颜色库中至少含有32 种颜色，从0～31 排序。同理，M=3，d=2 时，颜色库中至少含有64种颜色。

图4 图像子块编号与颜色编号的映射Fig.4 Mapping of image sub-blocks index and color index

1.4 求解含密B样条曲线控制点

本文算法以B 样条曲线的控制点作为特征隐藏秘密信息，因此需要提取含密曲线并求解其含密控制点以获得秘密信息。B 样条曲线的控制点数量比曲线上的采样点数量少得多，因此给定曲线上的一组采样点，可找到一组控制点生成B 样条曲线逼近该曲线，使其与原曲线的逼近误差最小化，可以将此过程视为一个最小二乘问题。曲线采样点的坐标可以用(m+1)×2的矩阵表示，具体为

式中，采样点个数为m+1 个。令C表示n+1 个控制点，则

然后，最小二乘的解可表示为

式中，B为n+1个控制顶点的基函数矩阵，表示矩阵的伪逆运算符号。由于在B 样条表示的x和y坐标可相互分离，故可对两坐标分别进行计算，具体为

求出B样条曲线的控制点坐标。

然而，当各采样点对应的B 样条基未知时，由曲线的同一组采样点和不同的样条基可以求出不同的控制点，且这些控制点生成的拟合B 样条曲线与原曲线近乎相同。因此，若无法实现采样点与B 样条基的正确对应，将无法求解生成该B 样条曲线的控制点。而B 样条基的值由参数决定，故此采样点与B 样条基的对应问题转化为采样点与参数的对应问题。

因此，本文算法引入参考B 样条曲线，利用参考曲线实现采样点与参数的初始对应及配准，并采用基于最近点迭代的方法（肖轶军 等，2000）优化采样点与参数的配准结果，通过最小二乘法求解出含密曲线的含密控制点坐标。

1.5 信息提取

为提取含密纹理图像中隐藏的秘密信息，接收方首先通过对图像的颜色提取和边缘检测操作获得初始控制点和含密曲线，然后对它们进行结合生成含密曲线的参考曲线，最后根据参考曲线反求出各含密曲线的控制点坐标，进而提取出秘密信息。

步骤1）获得初始控制点。将图像分块、编号并用密钥进行图像子块置乱。提取图像颜色并与颜色库进行相似度对比获得颜色索引，由本文提出的数组在颜色库中的映射规则获得子块编号，进而通过与信息隐藏操作相同的方式获得初始控制点C=。

步骤2）获得含密纹理曲线。排除颜色库中不存在的颜色所填充区域，对含密图像进行边缘检测，分别连接各曲线与图像边缘的两个交点，对任意连线长度r，若[r/N±β]≤min(k，2d)，则认为该纹理曲线中未隐藏秘密信息，并将此纹理曲线从检测获得的纹理曲线中删去，其中[·]为取整运算符，β为一个接近0 的预设参数，N为与发送方相同的预设参数。删除不含密曲线后即获得含密曲线集，记为Ss=，其中，v为含密曲线的条数，(ai，x，ai，y)和(bi，x，bi，y)分别为第i条含密曲线于图像边缘交点的位置坐标，连接各组交点获得Ss所对应的定位直线集L={l1，l2，…，lv}。对定位直线li(i=1，2，…，v)，记其长度为ri=‖li‖(i=1，2，…，v)，则含密曲线所含秘密信息的比特数qi=[ri/N]。由此可获得各含密曲线所隐藏秘密信息比特数，由Q={q1，q2，…，qv}表示。

步骤3）获得不含密参考曲线控制点。将初始控制点仿射变换至各定位直线位置，获得各参考曲线的控制点，经B 样条绘制即得到各含密曲线的参考曲线Sr=，将中间控制点数增至qi个，获得控制点集Cs=，其中。

2 实验结果及比较

本文实验均在Windows 10 操作系统下使用MATLAB2020a仿真软件完成，颜色库中颜色均取自优设网站，实验所用秘密信息为随机生成的二进制数据。本文算法适用于多种次数的B 样条曲线，由于n次B样条在节点处有n-1阶连续性，一般计算机绘图需求为连续二阶可导，且在曲线设计中，三次B样条曲线及其变形几乎可以应用到所有曲线造型场合，因此，实验选用三次B样条进行曲线绘制。

本文算法可生成多种尺寸的图像，将图像划分为2M×2M个子块且随机选取2d(d∈N)个子块时，需构建含有2M+d+1种颜色的颜色库。本实验生成512×512 像素图像，分为8×8 个图像子块，随机选择4 个子块生成初始控制点，故构造含有64 种颜色的颜色库，分别为颜色编号0～63。

2.1 本文算法结果

图5 展示了含密纹理图像的构造过程。实验首先在空白画布中构建笛卡儿坐标系，使画布的4 个顶点分别对应坐标（0，0），（0，512），（512，512），（512，0）。然后将画布均分为8×8个互不重叠的小块并顺序编号，再利用密钥将其置乱，置乱结果如图5（a）所示。d=2，即随机选取2d=4 个编号4，10，43，25，取这些编号对应图像子块的中点坐标（32，32），（160，32），（352，96），（480，32）。计算这4 个坐标点的拟合直线，且获得该直线与画布边缘的交点分别为（1，34.81）和（512，61.24），即获得6 个初始控制点（1，34.81），（32，32），（160，32），（352，96），（480，32），（512，61.24）。将拟合直线沿其法线方向等间隔地绘制出16 条平行的定位直线，如图5（b）所示，其中初始控制点在图中由圆圈标出。接着将初始控制点仿射变换至各定位直线位置，经B 样条曲线绘制后获得如图5（c）所示的参考纹理图像。

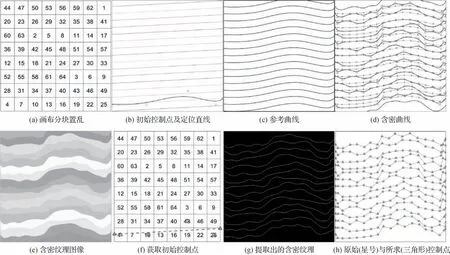
图5 本文算法各阶段实验结果Fig.5 Experimental results of the proposed algorithm with different stages（（a）block scrambling；（b）initial control points and positioning lines；（c）reference curves；（d）stego curves；（e）the stego texture image；（f）initial control points；（g）extracted stego textures；（h）original（star）and desired（triangle）control points）

实验预设密集参数N=30，信息隐藏时的控制点移动距离h=16，通过移动控制点位置进行信息隐藏操作，并对不可隐藏曲线及干扰曲线进行标记。图5（d）中的曲线即为含密曲线或经过扰动后的纹理曲线，图中三角形标记各含密曲线的控制点位置，星号标记参考曲线的控制点位置。最后从颜色库中提取图像块索引4，10，43，25 对应的编号分别为0、33、10、19、44、29、30、15 的颜色作为候选颜色，为扰动曲线对应区域填充不存在于颜色库中的颜色，为其他区域自上而下地进行候选颜色的轮流填充，最终构造出的含密纹理图像如图5（e）所示，该图中含14条含密曲线，共隐藏238 bits秘密信息。

在信息提取阶段，接收方用与发送方相同的方式将图像分块、编号和置乱，再提取图像颜色并根据数组在颜色库中的映射规则获得与发送方相同的初始控制点，如图5（f）所示，其中三角形标记初始控制点。接收方通过边缘检测和颜色对照提取出含密曲线，如图5（g）所示。根据含密曲线位置对初始控制点进行仿射变换及参考曲线绘制，进行最多30 次迭代，求解出各含密曲线的控制点。对比各含密曲线控制点及其对应参考曲线控制点的欧氏距离，距离大于8时提取秘密信息1，否则提取秘密信息0，由此即可提取含密纹理图像中隐藏的秘密信息。如图5（h）所示，星号标记了含密曲线的真实控制点，三角形标记了从含密曲线中求解的控制点，由图可知它们近乎重合，实验结果表明此实验可以完全准确地提取出含密纹理图像中隐藏的秘密信息。

2.2 隐藏容量分析及比较

本文算法的隐藏容量可根据生成图像的样式灵活调整，提高隐藏容量的方法有两个，其一为减小生成条纹间隔，通过在相同大小画布中绘制更多用于隐藏信息的条纹提高隐藏容量；其二为增多各曲线内的含密控制点数，再降低曲线平滑度的同时增加隐藏容量。

设生成含密纹理图像的密集参数为N，当生成图像中含有相同数量的可隐藏信息的曲线时，N越大生成曲线越平滑，隐藏容量越小，反之生成曲线越陡峭，隐藏容量越大。设定位直线集L中的任一长度为ri的定位直线，将满足[ri/N]＞min(k，2d)的曲线记为可隐藏秘密信息的B 样条曲线，且隐藏比特数为qi=[ri/N]，设含有v条含密曲线，由此构造集合Q=qi(i=1，2，…，v)，则一幅纹理图像中可隐藏信息比特数为。

如图6 所示，分别通过增多曲线数量和增多各曲线隐藏容量生成了隐藏容量更大的纹理图像，实验中分别将含密曲线数量增加至21 条，密集参数调整为30，生成的含密图像如图6（a）及图6（b）所示，这两幅含密图像中分别隐藏秘密信息423 bits 和850 bits。图6（c）将上述两种提高隐藏容量的条件组合起来，生成21 条含密曲线且密集参数为10，生成的纹理图像中共隐藏了1 239 bits信息。

图6 隐藏容量不同的含密图像Fig.6 Stego images with different hiding capacities（（a）v=21，N=30；（b）v=14，N=10；（c）v=21，N=10）

因此，本文算法具有灵活的隐藏容量，且生成的含密曲线越密集、各曲线的含密控制点越多，隐藏容量越大。故既可根据生成图像的复杂程度决定图像的隐藏容量，又可通过规定图像的隐藏容量生成复杂程度不同的含密纹理图像。

为进一步分析本文算法的隐藏容量，将本文算法与其他构造式信息隐藏算法相比较，实验结果如表1 所示。构造式信息隐藏算法的隐藏容量均与生成图像的尺寸有关，故对比生成图像均为800 ×800 像素时的隐藏容量。对比发现，本文所提算法的隐藏容量明显大于同为生成纹理图像的构造式信息隐藏算法（潘琳 等，2016；司广文 等，2020），当算法（Qian 等，2018b）稀疏度取0.03～0.3 时，其隐藏容量区间为800～8 000 bits，大于本文算法的隐藏容量。但本文算法与生成曲线数量及各曲线可隐藏控制点数有关，隐藏只需满足生成互不重叠的含密曲线，可通过提高曲线密集度和增多各曲线控制点数提高隐藏容量，或根据更改图像中参考条纹的形状使一条曲线中可隐藏更多信息。

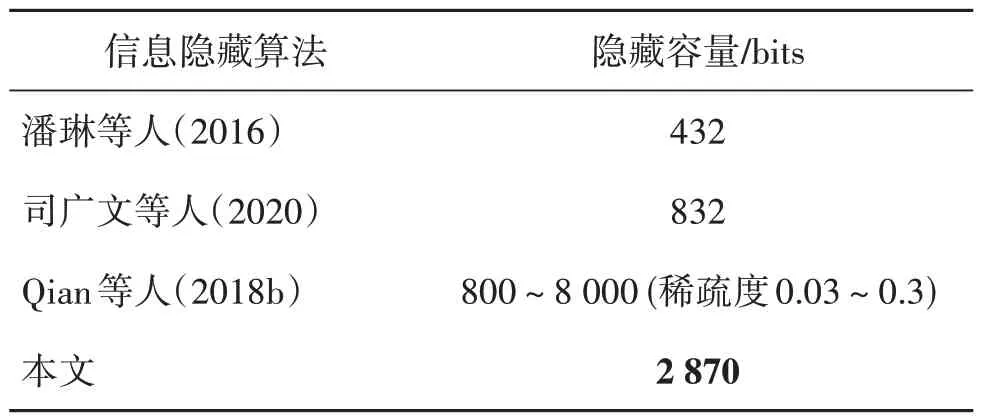
表1 不同算法构造800 × 800像素图像的隐藏容量比较Table 1 Comparison of hiding capacity of 800 × 800 pixels images constructed by different algorithms

2.3 鲁棒性分析及比较

含密图像在公共信道传输的过程中可能遭受图像攻击破坏，导致秘密信息无法准确提取。因此，抗常见图像攻击能力是衡量本构造式信息隐藏算法鲁棒性的一个重要指标。为验证本文算法生成纹理图像的鲁棒性，实验应用了一系列常见的图像攻击方法对生成的含密纹理图像进行模拟攻击。图7 为对含密图像攻击后的图像展示，其中，图7（a）为本文算法生成的未经攻击的含密纹理图像，图7（b）—（h）分别为对图7（a）进行JPEG 压缩（质量系数是50）、椒盐噪声（噪声密度是0.01）、图像缩放（比例是0.6）、均值滤波（模板大小是7×7）、中值滤波（窗口大小是7×7）、高斯滤波（窗口大小是7×7）、饱和度增强（增强比例30%）攻击后的图像。现从遭受模拟攻击的图像中提取信息，并通过计算误比特率（bit error rate，BER）来评估本文算法生成图像对各种图像攻击的鲁棒性，误比特率的计算为

图7 不同攻击下的含密纹理图像Fig.7 Attacked versions of stego texture images（（a）non-attacked image；（b）JPEG compression（50%）；（c）salt and pepper noise（0.01）；（d）image scaling（0.6）；（e）mean filtering（7×7）；（f）median filtering（7×7）；（g）Gaussian filter（7×7）；（h）saturation enhancement（30%））

式中，D为信息提取错误的比特数，L为秘密信息的总长度。

实验结果如表2 所示，在实验参数下，本文算法生成的含密纹理图像对JPEG 压缩、中值滤波、均值滤波、高斯滤波和饱和度增强均具有良好的鲁棒性，提取信息的误码率为0。且本文算法能否实现秘密信息的准确提取取决于能否准确求解含密曲线的含密控制点坐标，而准确求解含密控制点坐标的先决条件是获取准确的含密B 样条曲线。由于含密曲线为连续曲线，而构造出的图像为栅格图像，对其进行放缩比例较小的变换将导致栅格图像的分辨率过低，加剧连续曲线在栅格图像中的离散化程度，使从中获取的离散含密曲线与原始的连续曲线间存在较大偏差，致使含密控制点的错误求解，进而导致秘密信息的错误提取。而图像的放大变换则保留了含密曲线的细节特征，对曲线上各点的相对位置关系影响较小，因此能更准确地求解出含密控制点，并进行秘密信息的准确提取。故本文算法对含密图像的缩小变换具有较差的鲁棒性，而对放大变换的鲁棒性较强。

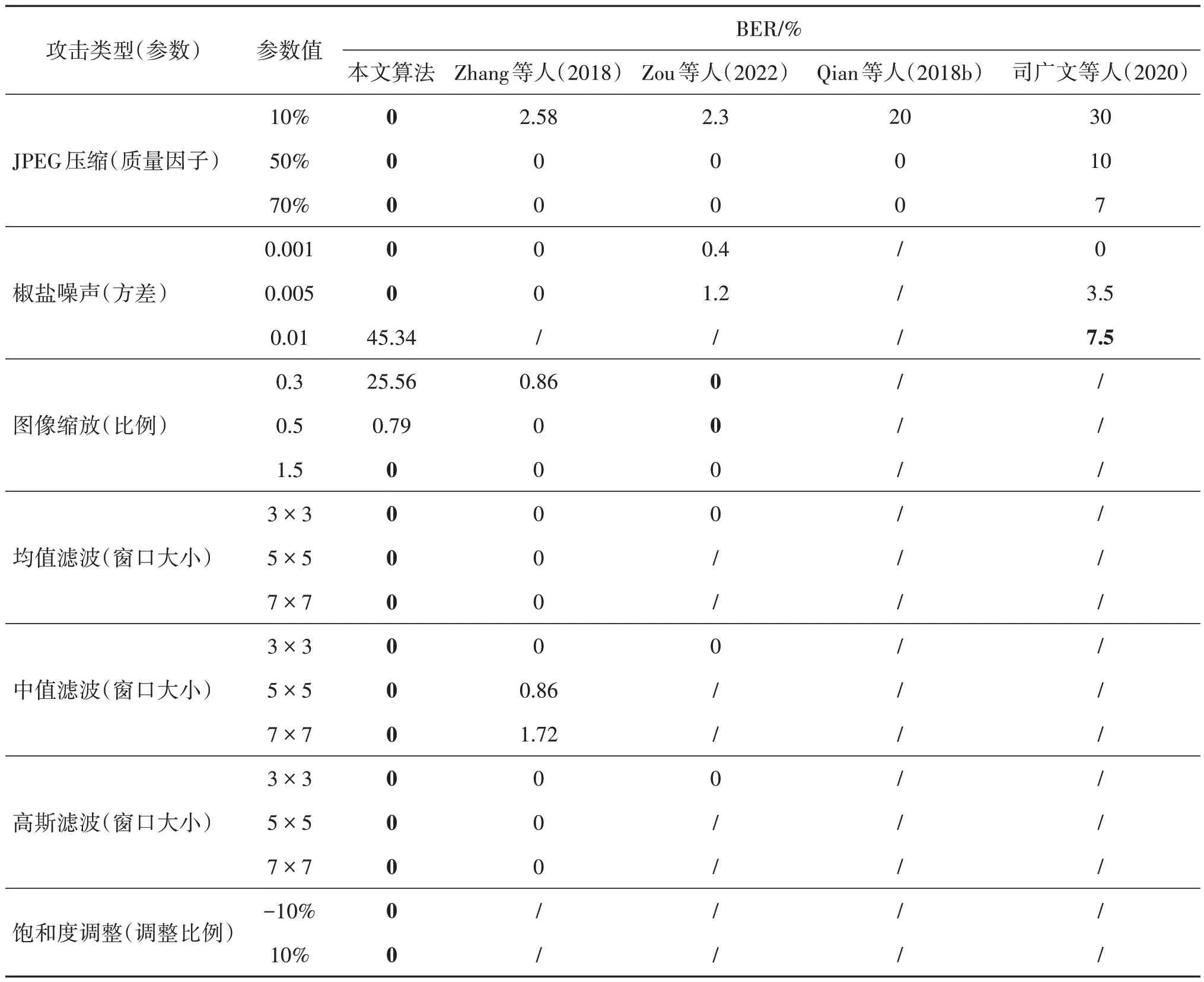
表2 本文算法与其他无载体信息隐藏算法抗常见图像攻击鲁棒性能的比较Table 2 Robustness comparison between the proposed algorithm and other coverless information hiding algorithms

此外，本文算法对椒盐噪声具有一定的鲁棒性，可以准确提取受密度在0.01 内的椒盐噪声攻击后图像中隐藏的秘密信息，但由于椒盐噪声为散点噪声，将对图像中含密曲线的准确提取造成影响，进而导致秘密信息的错误提取，故当噪声密度大于0.01时将无法从受椒盐噪声攻击的图像中提取出完全准确的信息，因此可在信息提取步骤前加入中值滤波操作滤除椒盐噪声，以提高信息提取准确性。经实验表明，在隐藏容量为100～400 bits的含密图像中，中值滤波操作可有效抵抗密度为0.02 的椒盐噪声的攻击，实现秘密信息的准确提取，故中值滤波操作可使含密图像的抗椒盐噪声攻击能力提升至中值滤波前的2倍。

为进一步检验本文算法较以往无载体信息隐藏算法抗常见图像攻击鲁棒性能的提升，将本文算法与选择式无载体信息隐藏算法（Zhang 等，2018；Zou等，2022）在Holidays数据集下的抗图像攻击鲁棒性和构造式无载体信息隐藏算法（Qian等，2018b；司广文等，2020）的抗图像攻击鲁棒性进行比较。如表2 所示。相比于对图像攻击具有较强鲁棒性的选择式信息隐藏算法，本文算法对图像空域攻击，如JPEG 压缩、中值滤波和椒盐噪声，较对比算法具有更强的鲁棒性，且本文算法具有一定抗图像饱和度调整的能力。同时，相比于两种类似的构造式信息隐藏算法，本文算法抗JPEG压缩和椒盐噪声的鲁棒性更强，且可抵抗更多种类图像攻击。

2.4 安全性分析

本文算法的安全性体现在3 个方面。首先，以B 样条曲线控制点为特征隐藏信息并绘制图像，由于B 样条曲线的控制点基本不位于生成曲线上，因此在未经过对完整曲线的相应运算时，将无法直接从图像空域中提取出秘密信息。

其次，对图像子块的置乱操作增大了攻击者求解初始B样条曲线控制点的难度。由于含密控制点的求解需结合含密曲线与参考曲线共同计算，因此，对图像子块的置乱操作将使攻击者难以获取准确的初始控制点，从而无法获得用于求解含密控制点的参考曲线，导致难以提取出准确的秘密信息。由于本文算法将图像划分为2M×2M个子块，选取其中2d(d∈N)个子块获得初始控制点，故在未获得正确密钥的情况下需穷举次才可获得与信息隐藏者相同的初始控制点，进而实现秘密信息的提取。

最后，本文所提构造式信息隐藏算法具有较好的抗隐写分析能力。由于SRNet（steganalysis residual network）算法（Boroumand 等，2019）是深度学习隐写分析中一种比较有代表性的新型隐写分析算法，且对JPEG 图像具有较好的检测能力，而本文实验生成图像为JPEG 图像，因此选用SRNet 进行本文算法的抗隐写分析检测实验。

在隐写分析实验中，以本文算法生成的含密纹理图像作为含密图像，以生成过程中未隐藏秘密信息的纹理图像作为不含密图像，利用SRNet 算法进行隐写检测，检测结果可由检测误差PE表示，其值越接近0.5 表明越难以分辨输入图像是否含密，即表明信息隐藏算法越不易被隐写分析检测。检测误差PE的计算为

式中，PFA和PMD分别为虚警率和漏检率。

实验利用本文算法生成的7组800×800像素的纹理图像建立数据集，各组均由不含密纹理图像和其对应的含密纹理图像构成，其中一组为2×1 000 幅图像构成的训练集，一组为2×100 幅图像构成的验证集，5组测试集均由2 × 100幅图像构成，其中隐藏的信息比特数分别为150、200、250和300，实验结果如表3所示。当生成的800×800像素的含密纹理图像隐藏容量小于250 bits 时，PE值均在0.5 附近，表明隐写分析模型难以对本文算法生成的含密与不含密纹理图像进行区分。因此本文所提出的构造式信息隐藏算法具有较强的抗隐写分析能力。

表3 本文算法在不同隐藏容量下的抗隐写分析能力Table 3 The ability of anti-steganalysis of the proposed algorithm under different hiding capacities

3 结论

本文算法以B 样条曲线的控制点为特征，在利用B 样条绘制纹理图像的同时，通过改变控制点位置在图像空域间接地隐藏信息，解决了传统构造式图像信息隐藏算法生成图像的空域特征与秘密信息关联性较强的问题，提高了算法的安全性。此外，本文算法的隐藏容量可随生成纹理图像的样式和复杂程度灵活调整。实验表明，本文算法相较于已有的传统构造式图像信息隐藏算法具有更强的鲁棒性，且能够抵抗更多种类型的图像攻击，同时具备较强的抗隐写分析能力。

但由于本文算法仅能生成纹理图像，因此仍存在生成图像样式单一的问题，且本文算法的隐藏容量依旧低于嵌入式信息隐藏，因此可通过增强生成图案的多样性等方法加以改进。另外，由于B 样条曲线为参数曲线，故可进一步将其拓展应用于生成含密矢量图像和含密3D图像等，以提升算法的多样性和适用性，满足当前科技发展的需求。