高层建筑施工过程中的混凝土徐变分析

2024-04-21大同市第四建筑工程有限责任公司山西大同037008

砖瓦 2024年4期

陈欣 (大同市第四建筑工程有限责任公司，山西大同 037008)

基于建筑施工技术和设计理论的发展，高层建筑在全球范围内得到大规模兴建[1]。在全球建筑高度前10 的建筑中，中国超高层建筑占6 栋，其中，中国台湾的台北101大厦位居第3，建筑高度为508m，结构高度为438m；上海环球金融中心位列第4，建筑高度达到492m，结构高度达到474m[2-3]。在城镇化的高速推进下，为缓解城市用地紧张问题，我国也修建了大量的高层、超高层建筑，结构形式也从20世纪70年代的钢筋混凝土框架结构、框架-剪力墙结构发展到20 世纪90年代以后的筒体结构、筒中筒结构、连体结构、多筒体结构、悬挑结构等众多形式。这些高层建筑在结构变得日益复杂的同时，其结构技术问题也变得更加复杂和严峻。高层建筑施工周期长、荷载大，结构的竖向刚度和竖向荷载是逐层形成的，在结构设计和分析中忽略施工过程对结构内力和变形的影响显得尤为不现实，特别是对于混凝土材料具有显著的徐变特性，合理的分析方法才能得到与实际相符的内力和变形控制效果，否则会造成结构的超限变形以及结构弯矩和剪力的突变，引起结构的损伤和破坏[4]。为此，考虑结构施工顺序和混凝土徐变对高层建筑结构变形和内力的影响成为目前的研究重点。

1 工程概况

宁夏回族自治区石嘴山市某高层建筑为单体商用办公楼，集写字楼、酒店式公寓和商业功能为一体，结构层高为95m，地上30 层，地下1 层，首层层高为5m，其余楼层层高为3m，建筑面积为40500m2，采用钢筋混凝土框架剪力墙结构，梁、板、柱和剪力墙均采用C30混凝土，混凝土弹性模量为3×104MPa，考虑混凝土龄期和徐变影响的混凝土弹性模量为2.8×104MPa，结构柱为方形柱，边长为600mm，梁尺寸为600mm×300mm，楼板厚度为150mm。结构柱的轴压比为0.7，剪力墙的配筋率为0.5%。

2 考虑施工过程的混凝土徐变分析方法

如图1（a）所示，在传统的结构工程设计及变形计算中，往往将结构作为一个整体分析对象，结构的刚度和荷载一次加载，结构建造完成后立即承受其设计荷载。在这种荷载加载模式下，结构所有的受力状态都是同时确定的，忽略了结构在施工过程中可能产生的应力积累和变形积累过程，也忽略了由于材料徐变和松弛等引起的长期效应，计算的内力和变形会产生与实际结果较大的偏差。如图1（b）所示，精确模拟施工过程的计算考虑了结构竖向刚度和竖向荷载的逐层变化，这种加载模式下特别适用于大型复杂高层结构的施工设计，在逐级加载过程中考虑了结构材料的黏性流动和滞后弹性引起的不可逆徐变，有利于对结构长期的变形进行预测和控制[5]。

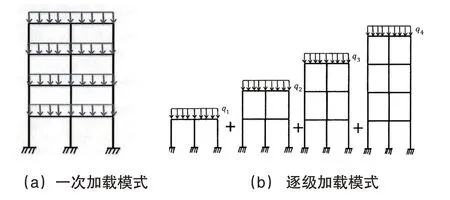
图1 结构内力和变形的不同分析模式

在逐级加载模式中，其内力和变形的技术运用了叠加原理，精确模拟施工过程为施作完成第1层，施加第1层结构外荷载{q1}，在此外荷载下作用下，结构产生内力{F1}和变形{△1}，两者的关系如公式（1）所示；继续施作完成第2 层，施加第2 层结构外荷载{q2}，在此外荷载下作用下，结构产生内力{F2}和变形{△2}，结构第2 层的内力与变形关系如公式（2）所示；结构第1层除了承担外荷载{q1}外，还需承担外荷载{q2}，因此，按照弹性叠加原理，结构第1层的内力和变形关系如公式（3）所示。

式中{F1}为结构第1 层的总内力矩阵；[K1]为结构第1层的总刚度矩阵；{△1}为结构第1 层的总位移矩阵；{F2}为结构第2 层的总内力矩阵；[K2]为结构第2 层的总刚度矩阵；{△2}为结构第2层的总位移矩阵；{F1,1}为第1层在完成第1层结构施工后的内力；{F2,2}为第2层在完成第2层结构施工后的内力；{F1,2+F2,2}为第1层完成第1层和第2层结构施工后的内力。

由此类推，可以得到第i层结构的最终内力{Fi}如公式（4）所示[6-7]。

在加载第j层荷载作用下，第i层结构的竖向变形差△di,j如公式（5）所示。

按照弹性叠加原理，可以得到结构第i层的最终竖向位移如公式（6）所示。

混凝土徐变是在持续荷载作用下结构的变形呈现非线性发展，具有早期发展速度快、持续时间长的特点，混凝土的徐变发生量主要集中在硬化后的3～6 个月，在2～3年后增长较慢，且持续时间可以达到数十年，徐变的发展过程可以大致用图2表示。混凝土的徐变过程可以用徐变函数表达，如公式（7）和公式（8）所示[8]。

图2 混凝土徐变发展过程

式中J(t,t0)为徐变函数；E(t0)为考虑徐变过程的混凝土弹性模量；φ(t,t0)为混凝土的徐变系数；εc(t,t0)为混凝土从t0时刻加载到t时刻产生的徐变应变；εe(t0)为混凝土在t0时刻的瞬时弹性应变。

3 混凝土徐变影响因素分析

3.1 轴压比对钢筋混凝土柱徐变的影响

钢筋混凝土柱的工作性能与其轴压比密切相关，结构轴力长期作用下导致了钢筋混凝土柱的持续变形[9]。为了研究轴压比对钢筋混凝土柱的徐变影响规律，运用结构计算软件SAP2000计算结构的徐变变形，设定5种不同的计算工况，分别为工况A（轴压比0.5）、工况B（轴压比0.6）、工况C（轴压比0.7）、工况D（轴压比0.8）、工况E（轴压比0.9），计算加载龄期为600d。图3为不同轴压比工况下结构柱的徐变变形量曲线。从图3可以看出，随着加载龄期的增加，结构柱的竖向变形呈现显著的分段变形规律，在20d 内，结构柱的竖向变形与加载龄期呈现显著的线性变化关系，而在20d之后，结构的竖向变形与加载龄期呈现近线性变化关系，其斜率远小于20d内的竖向变形直线斜率；结构柱的徐变变形与轴压比存在显著的关系，轴压比的不断增加，结构柱的竖向变形也不断增加，在工况A条件下，结构柱的最终竖向变形为2.34mm，而在工况E条件下，结构柱的最终竖向变形为4.24mm，增加约1倍。

图3 不同轴压比工况下结构柱的徐变变形量曲线

3.2 配筋率对剪力墙徐变的影响

钢筋混凝土配筋率可以降低混凝土的初始应力，增加结构的整体刚度，抑制剪力墙的收缩徐变变形。为了分析配筋率对剪力墙结构的徐变变形影响规律，设置4 种不同的计算工况，分别为工况I（配筋率0.25%）、工况II（配筋率0.5%）、工况III（配筋率0.75%）和工况IV（配筋率1.0%），轴压比为0.5，墙顶施加均布荷载为12MPa，竖向和水平钢筋均为HRB400 钢筋，加载时间为600d，剪力墙体厚度为300mm，长度3000mm，高度为3000mm，得到不同配筋率工况下剪力墙的徐变变形量曲线如图4所示。

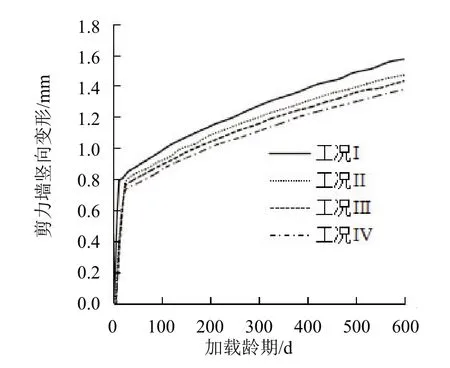
图4 不同配筋率工况下剪力墙的徐变变形量曲线

从图4可以看出，随着加载龄期的增加，剪力墙的竖向变形呈现显著的分段变形规律，在20d 内，剪力墙的竖向变形与加载龄期呈现显著的线性变化关系，而在20d之后，剪力墙的竖向变形与加载龄期呈现非线性变化关系，其增长速率逐步减缓；剪力墙的徐变变形与配筋率存在显著关系，配筋率不断增加，剪力墙的竖向变形不断减小，表明配筋率对混凝土结构徐变具有抑制作用，在工况I 条件下，剪力墙的最终竖向变形为1.57mm，而在工况IV 条件下，剪力墙的最终竖向变形为1.37mm，减少约13%。

3.3 混凝土强度对剪力墙徐变的影响

为了研究混凝土强度对剪力墙结构徐变变形的影响规律，设定了3 种不同的计算工况，分别为工况V（C30）、工况VI（C35）、工况VII（C40），计算得到混凝土强度工况下剪力墙的徐变变形量曲线，如图5所示。

图5 不同混凝土强度工况下剪力墙的徐变变形量曲线

从图5可以看出，随着加载龄期的增加，剪力墙的竖向变形呈现显著的分段变形规律，在20d 内，剪力墙的竖向变形与加载龄期呈现显著的线性变化关系，而在20d之后，剪力墙的竖向变形与加载龄期呈现非线性变化关系，其增长速率逐步减缓；提高混凝土强度对剪力墙的徐变变形有略微的降低，在工况V条件下，剪力墙的最终竖向变形为1.22mm，而在工况VII 条件下，剪力墙的最终竖向变形为1.19mm，减少约2%，这种降低可以忽略不计。