套筒灌浆连接装配式消能减震结构抗震性能研究
2024-04-21秦保静
房 良 秦保静
(青建集团股份公司,山东 青岛 266000)
在建筑产业发展经济、绿色和高效的时代背景下,预制装配式建筑通过将整体结构拆分为若干构件,并在工厂内标准化生产后运输至现场进行拼接和安装,这种生产模式与传统现浇混凝土结构最大的区别就是产品质量可控、施工效率高、施工周期短、环境污染小。因此,预制装配式建筑在我国逐步发展应用,受到国家和各地政府的大力推行,国内有关装配式建筑的研究也日益受到关注[1]。与现浇装配式建筑不同,预制装配式建筑需要在现场通过各种不同形式的节点连接方式将各个预制构件进行整体拼接,这些节点成为建筑抗震的薄弱环节,无法为建筑物提供有效的梁柱剪切刚度和水平侧向刚度[2-3]。
在装配式建筑结构中,套筒灌浆连接的结构形式应用最为广泛,为了提高这类连接方式的建筑抗震抗震性能,往往在节点中加入不同的消能减震结构,以提高结构的强度和刚度,其中,结构的层间位移角和剪应力是评价预制装配式结构最为重要的2个指标,前者为变形刚度指标,后者则为强度指标[4]。基于此,研究以山东省青岛市某装配式多层办公楼为研究对象,运用数值模拟的方法建立套筒灌浆连接装配式屈曲约束支撑计算模型,考虑了不同地震波输入的影响,分析结构的层间位移角、层间剪力等抗震性能参数,研究成果可应用于多层套筒灌浆连接装配结构的消能减震结构设计。
1 工程概况
山东省青岛市某装配式多层办公楼为钢筋混凝土框架结构,结构按8 度抗震设防标准设计,建筑结构层高均为4m,共10 层,总建筑高度为40m。建筑平面大致呈长方形,平面长度为80m,宽度为15m,建筑所在场地类别为二类场地,设计地震分组为第二组。建筑装配化率达到75%,属于高装配化建筑,设计使用年限为50年,预制构件承重形式分为预制竖向构件、预制水平向构件,预制竖向构件包括预制混凝土柱、预制混凝土墙板,预制水平向构件包括预制混凝土楼板、预制混凝土梁,所有预制构件的竖向接缝和水平接缝均采用套筒灌浆连接。为了满足建筑在多遇地震条件下,装配式混凝土框架结构的层间位移角小于1/550,罕遇地震条件下,层间位移角小于1/50,采用屈曲约束作为消能减震阻尼器,并在建筑中按照抗震不利节点(薄弱层)进行合理优化布置,以保证设置的屈曲约束支撑能够在结构损伤前发生屈曲破坏。如图1所示,消能减震器为BRB1型屈曲约束支撑,屈曲约束支撑加连接节点总长度为3.8m,芯材牌号为Q235,屈服段长度为2.4mm,屈曲承载力为400kN,设计承载力为448kN,设计位移为35mm,极限位移为42mm。

图1 屈曲约束支撑连接节点
2 套筒灌浆连接装配式消能减震结构有限元模型
为了研究套筒灌浆连接装配式建筑在安装屈曲约束支撑阻尼器条件下的减震抗震性能,以有限元分析软件ABAQUS 为研究手段,套筒灌浆连接装配式混凝土框架结构计算模型如图2所示。在建立的混凝土框架梁柱和楼板的基础上,采用杆件单元模拟屈曲约束支撑,装配式混凝土的梁柱的弹性模量为31.5GPa,泊松比为0.25,实测立方体抗压强度为43.7MPa,楼板的弹性模量为32.5GPa,泊松比为0.2,实测立方体抗压强度为38.9MPa,均采用混凝土塑性损伤模型(CDP 损伤模型)对混凝土材料性能进行模拟[5-6]。

图2 套筒灌浆连接装配式混凝土框架结构及屈曲约束支撑数值计算模型
地震波的特征表现在持续时间和最大地震动加速度上[7],仿真计算考虑了不同地震荷载作用下结构的抗震性能,选取了2 条实际地震波和1 条人工合成地震波,2 条实际地震波分别为1994 年的美国好莱坞地震波(工况A),地震动时长为34.81s,最大地震动加速度为0.17m/s2;1997 年意大利贝伐纳地震波(工况B),地震波时长为50.18s,最大地震动加速度为0.29m/s2;人工合成波(工况C)时长为32s,最大地震动加速度为0.23m/s2。3条地震波的时程曲线如图3所示。

图3 数值计算选取的3条地震波时程曲线
3 安装屈曲约束支撑的套筒灌浆连接装配式结构弹塑性时程分析
层间位移角反映了结构在地震波作用下的抗变形能力[8]。图4为安装屈曲约束支撑的套筒灌浆连接装配式结构在不同地震荷载作用下的层间位移角。从图4中可以看出,3 种不同地震波作用下,装配式结构X 向的层间位移角随着楼层高度的增加呈现一致的变化趋势,均表现为非线性单调增加后减小的规律,层间位移角峰值出现在约12m 高度处;由于工况A 的最大地震动加速度小于工况B 和工况C,工况B 和工况C 的最大地震动加速度相近,由此得到的装配式X 向的层间位移角在高度为8m 以下相近,而在高度8m 以上,工况B和工况C的层间位移角相近,但均大于工况A的层间位移角,工况A的层间位移角峰值为0.0013rad,工况B的层间位移角峰值为0.00142rad,工况C的层间位移角峰值为0.00163rad;与X 方向的层间位移角变化规律相比,装配式结构Y 方向的层间位移角随着楼层高度的变化明显不同,但地震波的形式对层间位移角的变化规律影响不明显;随着楼层高度的增加,装配式结构Y方向的层间位移角曲线 “双峰” 特征,在楼层高度约为12m和31m的位置出现极大值,而在24m的位置出现极小值;在12m 位置处,工况A 的层间位移角极大值为0.001rad,工况B的层间位移角极大值为0.00136rad,工况C的层间位移角极大值为0.00144;在31m位置处,工况A的层间位移角极大值为0.00124rad,工况B的层间位移角极大值为0.0013rad,工况C 的层间位移角极大值为0.00141rad;在24m 位置处,工况A 的层间位移角极小值为0.00089rad,工况B 的层间位移角极大值为0.00125rad,工况C的层间位移角极大值为0.00136rad;3种不同地震波作用下,装配式结构Y向的层间位移角在36m以上较为接近。

图4 不同地震荷载作用下装配式结构的层间位移角变化曲线
综合装配式结构X 方向和Y 方向的层间位移角变化曲线可知,在不同地震荷载作用下,结构层间位移角在两个方向的变化规律均不一致,结构呈现出显著的扭曲受弯趋势,这种扭曲变形差异在31m 位置处显得尤为明显。
装配式结构在地震波作用下主要通过框架柱之间的剪力提供消能[9-11]。图5为安装屈曲约束支撑的套筒灌浆连接装配式结构在不同地震荷载作用下的框架柱层间剪力变化曲线。从图5中可以看出,随着楼层高度的增加,装配式框架柱在X 向、Y 向上的剪力变化规律均呈现明显的单调非线性减小的趋势,在建筑物第一层的剪应力值最大;在相同的建筑高度位置处,框架柱层间剪力按照工况A、工况B 和工况C 的顺序逐步增加;在X方向上,工况A、工况B和工况C第一层装配式框架柱的剪力值分别为4476.7kN、5179.84kN、5906.65kN,在Y方向上,工况A、工况B和工况C第一层装配式框架柱的剪力值分别为4719.09kN、5572.79kN、5662.90kN。
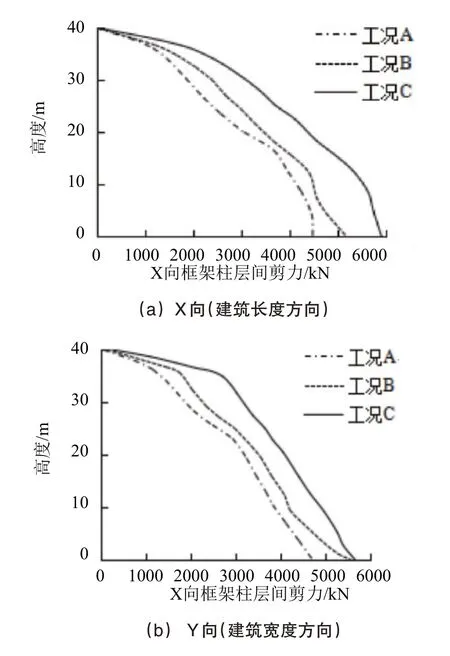
图5 不同地震荷载作用下装配式结构的框架柱层间剪力变化曲线
4 结语
以山东省青岛市某装配式多层办公楼为研究对象,运用数值模拟的方法建立了套筒灌浆连接装配式屈曲约束支撑计算模型,考虑了不同地震波输入的影响,分析结构层间位移角、层间剪力等抗震性能参数的变化规律,得到以下结论:
(1)3 种不同地震波作用下,装配式结构X 向的层间位移角随着楼层高度的增加均表现为非线性单调增加后减小的规律,层间位移角峰值出现在约12m 高度处;工况A的层间位移角峰值为0.0013rad,工况B的层间位移角峰值为0.00142rad,工况C的层间位移角峰值为0.00163rad。
(2)3 种不同地震波作用下,装配式结构Y 向的层间位移角随着楼层高度的增加均表现为 “双峰” 特征,在楼层高度约为12m和31m的位置出现极大值,而在24m的位置出现极小值;结构层间位移角在两个方向的不一致性,使得结构呈现出显著的扭曲受弯趋势。
(3)随着楼层高度的增加,装配式框架柱在X向、Y向上的剪力变化规律均呈现明显的单调非线性减小的趋势,在建筑物第一层的剪应力值最大,在相同的建筑高度位置处,框架柱层间剪力按照工况A、工况B 和工况C的顺序逐步增加。
