考虑动态需求的生鲜商品物流配送优化方法研究
2024-04-19王勇罗双苟梦圆罗思妤
王勇,罗双,苟梦圆,罗思妤
自动化与智能化技术
考虑动态需求的生鲜商品物流配送优化方法研究
王勇1,2,罗双1,苟梦圆1,2,罗思妤1
(1.重庆交通大学,重庆 400074;2.绿色物流智能技术重庆市重点实验室,重庆 400074)
针对生鲜商品配送过程中客户需求的变化,协调静态与动态客户需求之间的关系,合理规划路径,并降低物流总成本。首先考虑客户生鲜需求的多样化温控区间、随机订单请求时间及动态需求量等因素,构建物流总成本最小化的整数规划模型。然后,设计基于高斯混合聚类的改进蚁群算法求解该模型,并提出动态需求处理策略,用于路径的再优化。其次,通过与粒子群算法、遗传算法和鲸鱼优化算法进行对比分析,验证文中设计算法的有效性。最后,以重庆市某生鲜配送网络为例,对比分析优化前后的运营指标,并探讨生鲜商品价值损失水平与物流总成本之间的关系。经优化后,物流总成本下降了22.35%,其中惩罚成本、价值损失、配送成本和温控成本分别下降了39.84%、61.84%、29.80%、57.00%。文中所提的模型、算法和动态需求处理策略可以合理规划配送路径,有效降低了总成本,为考虑动态需求的生鲜配送网络优化提供了参考。
生鲜商品配送;动态需求;价值损失;高斯混合聚类;改进蚁群算法
随着经济社会的快速发展和人民生活水平的不断提高,生鲜商品的配送需求日益增加[1]。由于生鲜商品具有易腐性和时效性等特征,因此对配送过程的温度控制和即时性提出了严格要求。目前,生鲜商品的配送过程普遍存在客户需求多样化和动态变化情景(如新增客户需求,客户需求增加或减少等),而不合理的配送线路设计会导致客户需求服务延迟、配送过程温控成本增加及生鲜商品价值损失严重等问题。2021年农业农村部数据显示[2],由生鲜商品运输、存储和配送过程的不规范及保鲜措施的不足导致的生鲜商品价值损失率高达30%。可见,研究考虑动态需求的生鲜商品物流配送优化问题,并高效处理生鲜商品动态需求、合理规划生鲜商品配送车辆的路径,进而降低生鲜商品价值损失和物流配送运营成本显得尤为重要。国内外学者从生鲜商品配送路径优化问题和考虑动态需求的车辆路径问题2个方面展开了一系列研究工作。
在生鲜商品配送路径优化问题研究方面,方文婷等[3]构建了总成本最小化的冷链物流路径优化模型,设计了结合A*算法与蚁群算法的混合算法进行模型求解。李想等[4]考虑了配送距离和生鲜变质等因素,以总成本最小为优化目标,设计了模拟退火算法进行模型求解。Qi和Hu[5]从减少资源调度时间的角度,构建了价值损失最小化的数学模型,并设计了改进的蚁群算法进行模型求解。Liang等[6]构建了配送成本最小化和客户满意度最大化的双目标模型,并提出了一种基于约束的混合元启发式算法进行求解模型。由上述文献可知,大部分研究集中考虑了静态客户需求的生鲜商品配送路径优化问题,而结合客户动态需求研究生鲜商品物流配送问题还有待进一步拓展。
在考虑动态需求的车辆路径问题研究方面,林明锦等[7]针对新增的客户需求和原有客户需求变动的问题,构建了车辆使用数量和行驶距离最小化的双目标优化模型,并提出了并行算法和模拟退火算法相结合的混合算法求解模型。丁秋雷等[8]针对不确定的客户需求,构建了最小化配送成本和最大化客户满意度的数学模型,并应用包含蚁群算法和邻域交换法的混合启发式算法进行模型求解。范厚明等[9]考虑了订单释放时间的不确定性,建立了最小化配送时间和行驶距离的两阶段优化模型,并设计了一种改进的邻域搜索算法进行模型求解。Xiang等[10]以总成本最小化为目标,提出了一种改进的蚁群算法进行研究。Wang等[11]考虑了时间窗和动态需求的车辆路径问题,建立了最小化行驶距离和客户等待时间的双目标优化模型,并设计了基于集成学习的动态多目标优化算法求解模型。由上述文献可知,混合启发式算法能够克服单一启发式算法的局限性,提高求解效率,且常被用于求解考虑动态需求的车辆路径问题,为文中研究的考虑动态需求的生鲜商品物流配送优化问题提供了理论支持。
文中研究考虑动态需求的生鲜商品物流配送优化问题,首先结合价值损失、温控成本和动态需求的插入成本,构建总成本最小化的整数规划模型。其次,设计基于高斯混合聚类的改进蚁群算法(Improved ant colony algorithm based on Gaussian mixture clustering,GMC-IACO)求解上述模型,并提出动态需求处理策略,用于调整路径,以服务各类动态需求。然后,为了验证GMC-IACO算法的有效性,与粒子群算法(Particle Swarm Optimization,PSMO)、遗传算法(Genetic Algorithm,GA)和鲸鱼优化算法(Whale Optimization Algorithm,WOA)进行对比分析。最后,结合实例,对比分析优化前后的配送成本、价值损失和温控成本等指标,并进一步分析价值损失水平与总成本之间的关系,拟为考虑动态客户需求的生鲜物流车辆路径优化问题提供决策支持。
1 问题描述
考虑动态需求的生鲜商品物流配送网络包含生鲜配送中心和一系列客户,客户的生鲜商品需求可分为静态客户需求和动态客户需求2类。其中,静态客户需求在配送服务开始前出现,且其需求量不变;动态客户需求是在配送过程中出现的,可以细分为3种类型,第1类动态客户需求指需求量临时减少的客户需求;第2类动态客户需求指需求量临时增加的客户需求;第3类动态客户需求指在配送服务开始后才出现的新增客户需求。此外,结合生鲜商品类型和生鲜商品运输过程中的温控要求,这里选择3类生鲜商品进行配送服务,具体包括樱桃、葡萄和玉米等生鲜果蔬(1~5 ℃),冷冻水饺、冰激淋等生鲜商品(−10~−6 ℃),冷冻海鲜、肉禽等生鲜肉制品(−20~−15 ℃)。结合客户生鲜商品需求的动态性和配送温度要求,优化生鲜商品的配送路径。考虑了动态客户需求的生鲜商品物流配送优化前后对比如图1所示。
在优化考虑动态需求的生鲜商品物流配送网络前(图1a),不同温控区间的生鲜商品混合配送,导致价值损失增加,如路线D→9→8→7→D中,客户8、9的生鲜需求温控区间为−10~−6 ℃,而客户7的生鲜需求温控区间为−20~−15 ℃,其中D表示配送中心。配送中心派遣新的车辆服务动态客户需求,导致配送路线迂回交错、时间窗违背现象突出,增加了车辆使用数量和时间窗惩罚成本。在优化考虑动态需求的生鲜商品物流配送网络后(图1b),通过动态客户需求处理策略调整了各配送路径,消除了配送路径交叉和车辆违反客户时间窗的现象,减少了生鲜商品价值损失和车辆使用数量。
假设配送车辆的租赁成本为140元/辆,单位时间的配送成本和惩罚成本分别为40、10元,单位动态需求的插入成本为15元。温控区间分别为1~5 ℃、−10~−6 ℃、−20~−15 ℃的生鲜商品,其单位商品价格分别为18、25、30元,新鲜度系数分别为0.2、0.3、0.1,单位时间温控成本分别为5、10、15元。由于这里涉及的客户数量和需求量较少,因此结合不同温控区间的生鲜商品特征指派相应的生鲜配送车进行服务,且客户需求的增加未超过车辆装载量限制。优化前后的相关运营指标如表1所示。
由表1可知,经优化后车辆使用数量从4辆降至3辆,总成本从1 772.9元降至1 314.1元。其中,价值损失、配送成本和租赁成本分别降低了10.00%、31.82%、25.00%。
2 模型建立
2.1 模型假设
在生鲜商品配送过程中,车辆从生鲜配送中心出发依次服务客户,在满足生鲜配送线路上的静态和动态客户需求后返回配送中心。相关模型假设如下所述。
1)静态客户需求的相关信息(温控区间、服务时间窗和地理坐标等)在配送中心开始服务前已知。当配送中心开始服务后,动态客户需求在配送中心服务时间窗内出现[12],且相关信息可知。
2)动态客户需求包含3种类型的需求,第1种类型为需求量增加的客户需求;第2种类型为需求量减少的客户需求;第3种类型为新增客户需求。第1种和第2种类型的生鲜商品需求仅考虑增加同一温控区间的商品,且同一温控区间的生鲜商品无差别。
3)生鲜商品配送车是单温区冷藏车,且生鲜配送车辆在服务完最后一个客户需求后,在返回配送中心的过程中不再计算温控成本[13]。
4)生鲜商品的价值损失与配送行程时间呈正相关。
2.2 符号定义
模型构建相关变量定义如表2所示。

图1 考虑动态客户的生鲜商品物流配送网络优化前后
表1 考虑动态客户需求的生鲜物流配送网络优化前后运营指标

Tab.1 Operating indicators of fresh commodity distribution network considering dynamic customer demands before and after optimization
表2 变量定义

Tab.2 Variable definitions
2.3 模型构建
以总成本最小化为目标,构建了考虑动态客户需求的生鲜商品物流配送优化模型,具体见式(1)。

式中:1为配送成本,计算见式(2);2为价值损失,计算见式(3);3为动态客户需求的插入成本和配送车辆的租赁成本,计算见式(4);4为温控成本,计算见式(5);5为时间窗惩罚成本,计算见式(6)。

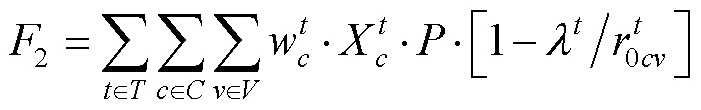



约束条件见式(7)~(25)。














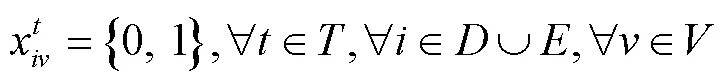

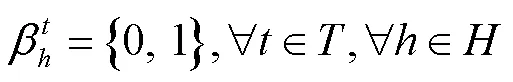

式(7)表示消除子回路,式(8)表示每个客户仅被访问1次,式(9)表示节点流量守恒,式(10)表示车辆服务的需求量不超过该车辆的最大载重量,式(11)表示所有客户的需求总量不超过配送中心的最大配送量,式(12)表示车辆使用数的计算,式(13)~(14)表示车辆到达客户的时间约束,式(15)~(16)表示车辆在配送中心时间窗内进行服务,式(17)表示动态客户需求在配送中心服务时间窗内产生,式(18)表示不用服务需求量减为0的客户,式(19)表示单个动态客户需求的需求量不超过车辆最大装载量,式(20)~(25)表示决策变量。
3 基于高斯混合聚类的改进蚁群算法
针对考虑动态客户需求的生鲜商品物流配送优化问题,这里设计了GMC-IACO算法进行求解。首先,应用高斯混合聚类(Gaussian mixture clustering,GMC)算法按照配送温度和地理位置将客户划分到不同的簇。然后,在各个簇中,结合动态客户需求处理策略,通过改进蚁群算法(Improved ant colony algorithm,IACO)规划路径。GMC-IACO算法流程如图2所示,其中,max表示最大迭代次数,max表示聚类最大迭代次数,max表示蚂蚁总数。
3.1 高斯混合聚类
GMC算法基于概率分布进行簇的划分[14],每个簇对应不同的高斯分布(即多元正态分布)。首先,假设簇的数量等于温控区间数量,通过式(26)计算高斯混合密度概率。其次,应用式(27)计算客户在各分布的条件概率,将客户分配到最大条件概率对应的分布内。然后,应用式(28)更新相关参数,并进行迭代,直至达到最大迭代次数。最后,根据式(29)将客户划分到相应的簇中。

式中:为高斯分布数量;为客户;α=1/;μ为簇的均值向量;∑为簇的协方差矩阵。

式中:z为客户所属的高斯分布。


式中:γ为客户符合分布的概率。
3.2 改进的蚁群算法

3.3 算法检验
为了验证GMC-IACO算法的有效性,将该算法与PSO[19]、GA[20]和WOA[21]算法进行比较。这里修改了Solomon数据集[22]中的20组测试数据,假设配送中心有3类生鲜商品,其温控区间分别为−20~−15 ℃、−12~−7 ℃、−3~2 ℃,对应商品的价格依次为18、15、7元/kg,算例特征如表4所示。算法参数设置如表5所示,每组算例计算15次,选择最优的结果进行比较,如表6所示。
表3 IACO算法伪代码

Tab.3 Pseudocode of IACO algorithm
表4 数据集特征

Tab.4 Characteristics of datasets
表5 参数设置

Tab.5 Parameter settings
表6 不同算法结果比较
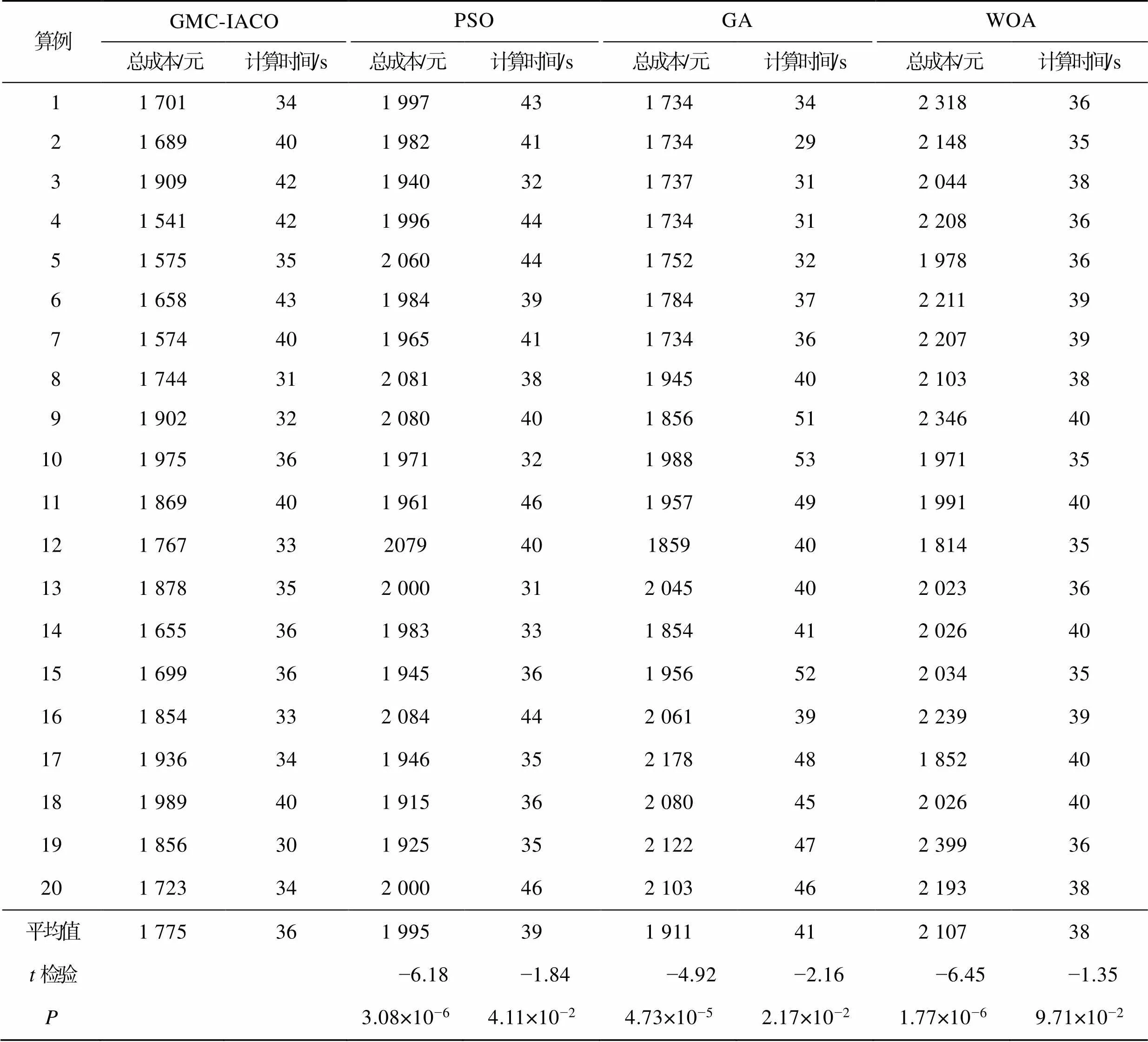
Tab.6 Comparison of different algorithm results
由表6可知,在总成本上,GMC-IACO算法结果的均值为1 775元,相较于PSO、GA、WOA算法结果的均值分别降低了11.03%、7.12%、15.76%;GMC-IACO算法的平均计算时间为36 s,PSO、GA、WOA算法的平均计算时间分别为39、41、38 s。由检验和的统计分析结果可知,GMC-IACO算法与其他3种算法的计算结果存在差异。由此可见,在求解考虑动态客户需求的生鲜商品配送优化问题方面,GMC-IACO算法具有更好的寻优能力。
4 实例分析
4.1 实例数据

表7 客户点特征

Tab.7 Characteristics of customers

图3 配送中心与客户地理位置分布
4.2 优化结果
基于上述配送中心及客户点信息,根据客户生鲜需求的配送温度和地理坐标划分客户,聚类结果如图4所示。
如图4所示,通过GMC算法聚类后,各个客户被分配到相应的温控区间,温控区间为−20~−15 ℃、−12~−7 ℃、−3~2 ℃的静态客户需求数量分别为30、30、25个,且相应动态客户需求数量分别为15、9、11个。考虑动态客户需求的生鲜商品优化后配送路线与优化前后的指标值如表8、9所示。
由表8和表9可知,经优化后总成本下降了22.35%。其中,惩罚成本、价值损失、配送成本和温控成本分别下降了39.84%、61.84%、29.80%、57.00%。由此可见,通过GMC-IACO算法进行路径规划,可有效降低成本、提高配送效率。

图4 聚类结果
表8 考虑动态客户需求的生鲜商品优化后配送路线

Tab.8 Optimized routes of fresh commodity distribution considering dynamic customer demands
注:*表示新增客户需求;^表示需求量增加的客户;#表示需求量减少的客户。
表9 考虑动态客户需求的生鲜商品配送优化前后结果对比

Tab.9 Comparison of results of fresh commodity distribution considering dynamic customer demands before and after optimization
4.3 价值损失水平的敏感度分析
这里选取温控区间为−20~−15 ℃内的客户点,分析讨论生鲜商品不同价值损失水平对总成本的影响。设置价值损失数值在150~200范围内为低水平价值损失、在201~250范围内为中等水平价值损失、在251~300范围内为高水平价值损失。总成本和价值损失水平关系如图5所示。
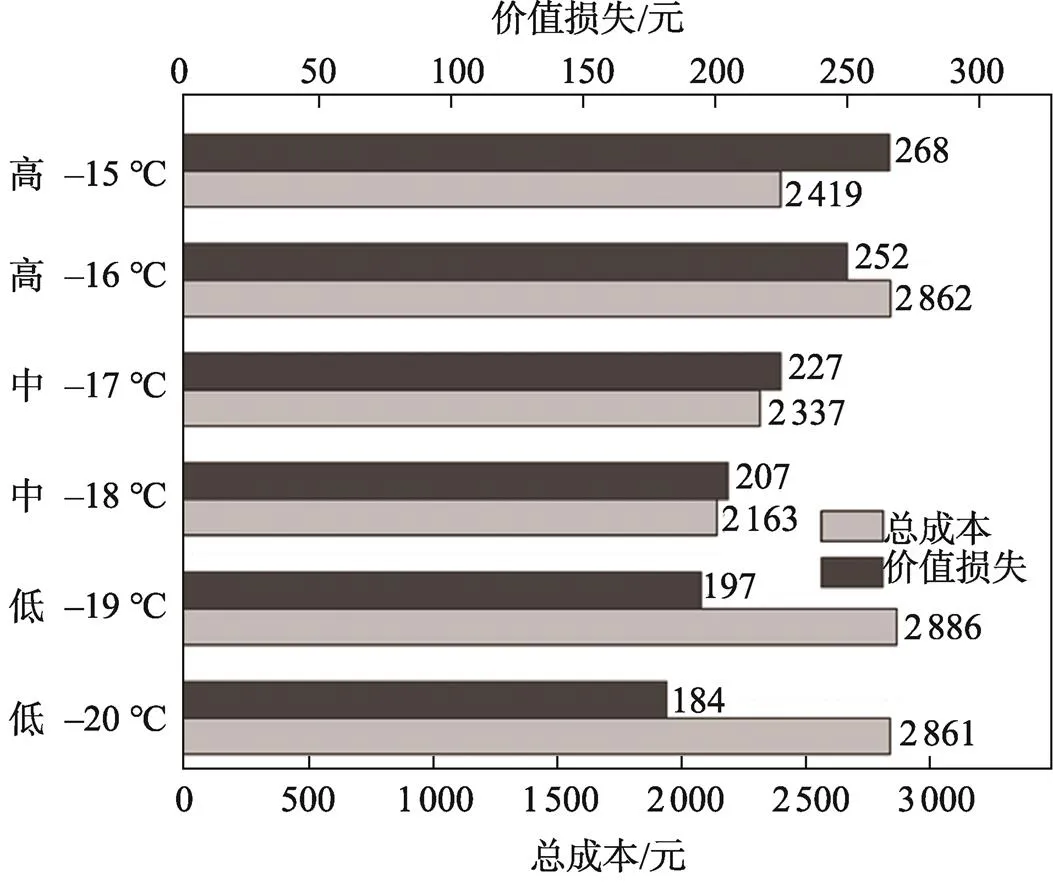
图5 总成本与价值损失的关系
由图5可知,相较于高水平价值损失和中等水平价值损失情况,低水平价值损失的总成本最高;在高水平价值损失下,其总成本高于中等水平价值损失下的总成本;在中等水平价值损失下,其总成本最低。由此可见,将价值损失设置为中等水平,能够同时保障生鲜商品的新鲜度、降低总成本。
5 结论
考虑了配送过程中需求的动态性,研究了考虑动态客户需求的生鲜商品物流配送优化问题,构建了总成本最小化的数学模型,并提出了包含动态客户需求处理策略的GMC-IACO算法求解模型。基于改进的Solomon算例,将GMC-IACO算法与PSO、GA、WOA算法进行了比较分析,验证了算法的有效性。最后,分析了重庆市某配送网络优化前后的结果,经优化后总成本下降了22.35%,价值损失和温控成本分别下降了61.84%、57.00%。同时,进一步探讨了价值损失水平对总成本的影响,结果显示,设置中等价值损失水平可以有效降低总成本。文中研究可为处理生鲜商品配送过程中的动态客户需求提供新思路和方法借鉴。
[1] ZHANG Y D, FAN X M, MA Y H, et al. Spatial Impacts of Cold Chain Logistics for Fresh Agri-Products on Carbon Emissions[J]. Transportation Research Part D: Transport and Environment, 2022, 113: 103525.
[2] 张倩, 熊英, 何明珂, 等. 不确定需求生鲜电商配送路径规划多目标模型[J]. 系统仿真学报, 2019, 31(8): 1582-1590.
ZHANG Q, XIONG Y, HE M K, et al. Multi-Objective Model of Distribution Route Problem for Fresh Electricity Commerce under Uncertain Demand[J]. Journal of System Simulation, 2019, 31(8): 1582-1590.
[3] 方文婷, 艾时钟, 王晴, 等. 基于混合蚁群算法的冷链物流配送路径优化研究[J]. 中国管理科学, 2019, 27(11): 107-115.
FANG W T, AI S Z, WANG Q, et al. Research on Cold Chain Logistics Distribution Path Optimization Based on Hybrid Ant Colony Algorithm[J]. Chinese Journal of Management Science, 2019, 27(11): 107-115.
[4] 李想, 闵德权, 张祺. 随机需求下半开放式冷链物流车辆路径优化[J]. 包装工程, 2022, 43(7): 160-169.
LI X, MIN D Q, ZHANG Q. Routing Optimization of Semi-Open Cold-Chain Logistics Vehicle under Random Demand[J]. Packaging Engineering, 2022, 43(7): 160-169.
[5] QI C M, HU L S. Optimization of Vehicle Routing Problem for Emergency Cold Chain Logistics Based on Minimum Loss[J]. Physical Communication, 2020, 40: 101085.
[6] LIANG X Y, WANG N M, ZHANG M, et al. Bi-Objective Multi-Period Vehicle Routing for Perishable Goods Delivery Considering Customer Satisfaction[J]. Expert Systems with Applications, 2023, 220: 119712.
[7] 林明锦, 王建新, 王超. 考虑动态度和时间窗的两级车辆路径问题[J]. 计算机集成制造系统, 2022, 28(6): 1870-1887.
LIN M J, WANG J X, WANG C. Two-Echelon Vehicle Routing Problem with Time Window Considering Dynamic Degree[J]. Computer Integrated Manufacturing Systems, 2022, 28(6): 1870-1887.
[8] 丁秋雷, 胡祥培, 位娟, 等. 动态需求下蓄冷式多温共配多目标优化模型及算法[J]. 运筹与管理, 2021, 30(12): 13-19.
DING Q L, HU X P, WEI J, et al. Research on Multi-Objective Optimization Model and Algorithm of Cold Storage Multi-Temperature Joint Delivery under Dynamic Demand[J]. Operations Research and Management Science, 2021, 30(12): 13-19.
[9] 范厚明, 咸富山, 王怀奇. 动态需求下考虑订单聚类的外卖配送路径优化[J]. 系统仿真学报, 2023, 35(2): 396-407.
FAN H M, XIAN F S, WANG H Q. Takeout Distribution Routes Optimization Considering Order Clustering under Dynamic Demand[J]. Journal of System Simulation, 2023, 35(2): 396-407.
[10] XIANG X S, QIU J F, XIAO J H, et al. Demand Coverage Diversity Based Ant Colony Optimization for Dynamic Vehicle Routing Problems[J]. Eng Appl Artif Intell, 2020, 91: 103582.
[11] WANG F, LIAO F S, LI Y X, et al. An Ensemble Learning Based Multi-Objective Evolutionary Algorithm for the Dynamic Vehicle Routing Problem with Time Windows[J]. Computers & Industrial Engineering, 2021, 154: 107131.
[12] WANG Y, ZHE J Y, WANG X W, et al. Collaborative Multicenter Reverse Logistics Network Design with Dynamic Customer Demands[J]. Expert Systems with Applications, 2022, 206: 117926.
[13] 王勇, 张杰, 刘永, 等. 基于资源共享和温度控制的生鲜商品多中心车辆路径优化问题[J]. 中国管理科学, 2022, 30(11): 272-285.
WANG Y, ZHANG J, LIU Y, et al. Optimization of Fresh Goods Multi-Center Vehicle Routing Problem Based on Resource Sharing and Temperature Control[J]. Chinese Journal of Management Science, 2022, 30(11): 272-285.
[14] 王宏伟, 柴秀俊. 基于高斯混合模型聚类的非均匀采样系统的多模型切换辨识[J]. 控制与决策, 2021, 36(12): 2946-2954.
WANG H W, CHAI X J. Multi-Model Switching Identification for Non-Uniformly Sampled Systems Based on Gaussian Mixture Model Clustering[J]. Control and Decision, 2021, 36(12): 2946-2954.
[15] 刘琳, 贾鹏, 高犇, 等. 新鲜度限制约束下物流配送中心选址-路径优化[J]. 包装工程, 2022, 43(5): 232-241.
LIU L, JIA P, GAO B, et al. Location Routing Optimization of Logistics Distribution Center under Freshness Limitation[J]. Packaging Engineering, 2022, 43(5): 232-241.
[16] 王书勤, 黄茜. 军事定向越野路径优化问题建模及混合蚁群算法求解[J]. 运筹与管理, 2018, 27(4): 105-111.
WANG S Q, HUANG Q. Route Optimization Model of Military Orienteering and Its Solution to a Hybrid Ant Colony Algorithm[J]. Operations Research and Management Science, 2018, 27(4): 105-111.
[17] 李阳, 范厚明, 张晓楠. 动态需求下车辆路径问题的周期性优化模型及求解[J]. 中国管理科学, 2022, 30(8): 254-266.
LI Y, FAN H M, ZHANG X N. A Periodic Optimization Model and Solution for Capacitated Vehicle Routing Problem with Dynamic Requests[J]. Chinese Journal of Management Science, 2022, 30(8): 254-266.
[18] 陈萍, 董文哲, 于信尧. 新能源移动充电车路径优化问题研究[J]. 运筹与管理, 2020, 29(2): 12-18. CHEN P, DONG W Z, YU X Y. Study on Routing Problem for New Energy Mobile Charging Vehicles[J]. Operations Research and Management Science, 2020, 29(2): 12-18.
[19] 杨健健, 唐至威, 王子瑞, 等. 基于VSPSO和A-G网络的掘进机动态路径规划[J]. 控制与决策, 2019, 34(3): 642-648.
YANG J J, TANG Z W, WANG Z R, et al. Dynamic Path Planning of Roadheader Based on VSPSO and A-G Net[J]. Control and Decision, 2019, 34(3): 642-648.
[20] 王勇, 罗思妤, 周雪, 等. 多中心共同配送开闭混合式的车辆路径优化问题[J]. 系统管理学报, 2023, 32(2): 215-232.
WANG Y, LUO S Y, ZHOU X, et al. Open-Closed Hybrid Vehicle Routing Optimization of Multi-Center Joint Distribution[J]. Journal of Systems & Management, 2023, 32(2): 215-232.
[21] 刘景森, 马义想, 李煜. 改进鲸鱼算法求解工程设计优化问题[J]. 计算机集成制造系统, 2021, 27(7): 1884-1897.
LIU J S, MA Y X, LI Y. Improved Whale Algorithm for Solving Engineering Design Optimization Problems[J]. Computer Integrated Manufacturing Systems, 2021, 27(7): 1884-1897.
[22] SOLOMON M M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints[J]. Operations Research, 1987, 35(2): 254-265.
[23] 蒋海青, 赵燕伟, 徐兆军, 等. 动态需求低碳开放式选址−路径问题[J]. 计算机集成制造系统, 2020, 26(1): 202-212.
JIANG H Q, ZHAO Y W, XU Z J, et al. Dynamic Demand Open Location-Routing Problem Considering Carbon Emissions[J]. Computer Integrated Manufacturing Systems, 2020, 26(1): 202-212.
[24] 任腾, 陈玥, 向迎春, 等. 考虑客户满意度的低碳冷链车辆路径优化[J]. 计算机集成制造系统, 2020, 26(4): 1108-1117.
REN T, CHEN Y, XIANG Y C, et al. Optimization of Low-Carbon Cold Chain Vehicle Path Considering Customer Satisfaction[J]. Computer Integrated Manufacturing Systems, 2020, 26(4): 1108-1117.
Fresh Commodity Logistics Distribution Optimization Considering Dynamic Demands
WANG Yong1, 2, LUO Shuang1, GOU Mengyuan1, 2, LUO Siyu1
(1. Chongqing Jiaotong University, Chongqing 400074, China; 2. Chongqing Key Laboratory of Green Logistics Intelligent Technology, Chongqing 400074, China)
The work aims to coordinate the relationship between static and dynamic customer demands in view of the changes in the customer demands for the fresh commodity distribution, and plan the path reasonably and reduce the total logistics cost. Firstly, an integer programming model was established for minimizing the total logistics cost in consideration of the diverse temperature control intervals, random order request time, and dynamic customer demands quantity. Then, an improved ant colony algorithm based on Gaussian mixture clustering was designed to solve this model, and a dynamic demands processing strategy was proposed to re-optimize routes. Next, the effectiveness of the proposed algorithm was verified through comparison with particle swarm optimization, genetic algorithm and whale optimization algorithm. Finally, with the fresh commodity distribution network in Chongqing as an example, the operational indicators before and after optimization were compared and analyzed. Besides, the relationship between the value loss level of fresh commodity and the total logistics cost was explored. After optimization, the total logistics cost decreased by 22.35%, in which the penalty cost, the value loss, distribution cost and temperature control cost reduced by 39.84%, 61.84%, 29.80% and 57.00%, respectively. The proposed model, algorithm and dynamic demands processing strategy can reasonably plan routes and effectively reduce the total cost, which provides a methodological reference for fresh commodity distribution network optimization with dynamic demands.
fresh commodity distribution; dynamic demands; value loss;Gaussian mixture clustering; improved ant colony algorithm
TP18;F570
A
1001-3563(2024)07-0148-11
10.19554/j.cnki.1001-3563.2024.07.019
2023-10-10
国家自然科学基金(72371044,71871035);重庆市教委科学技术研究重大项目(KJZD-M202300704);重庆市自然科学基金面上项目(CSTB2022NSCQ-MSX0535);巴渝学者青年项目(YS2021058);智能物流网络重庆市重点实验室开放基金(KLILN2023ZD003)
