基于对称性评价的曲线对称中心拟合算法
2024-04-18刘海波夏玉国
张 鑫, 刘海波,2,3, 夏玉国
(1.武汉地震计量检定与测量工程研究院,湖北 武汉 430071;2.湖北省地震局,湖北 武汉 430071;3.中国地震局地震研究所 地震大地测量重点实验室,湖北 武汉 430071)
1 引 言
在机器视觉中,目标位置的探测是核心问题之一。其中,一维图像(即灰度曲线)中的目标位置探测,是相关任务中的基础性问题[1]:一方面,很多基于线阵图像传感器的应用,仅能获取一维图像,需要获取其目标位置[2,3];另一方面,在二维图像目标位置探测中,也经常会采用在图像中作灰度剖面的方法,将二维探测问题转换为一维探测问题[4~12]。一维图像中的目标位置探测,常用的方法有边缘探测法、阈值法、极值法、曲线拟合法、灰度质心(centroid)法。边缘探测法、阈值法与极值法均利用曲线局部信息实现曲线中心探测,边缘探测法通常用于灰度曲线具有陡峭边缘的情况,极值法适用于具有局部光滑凸起顶部/凹陷底部的曲线,而阈值法更适用于曲线具有良好对称性的情况,这3种方法都容易受到局部噪声的干扰,适用范围有限[2~5,13];曲线拟合法适用于对图像形状具有某些先验信息的情形,如在高斯光束成像的位置探测中,可以假设一维图像为高斯曲线,曲线拟合所使用的算法因拟合曲线的类型而异,但都会使用曲线的大部分乃至全部信息,在曲线形状符合先验假设的情况下具有较高精度,除了曲线中心位置外,通常还需要将曲线幅度及水平尺度相关的系数作为待求参数,有时还需要引入非线性的数学模型,算法复杂,计算量相对较大[8~10,14,15];灰度质心法不需要对曲线形状进行先验假设,它无需迭代,计算速度快,在光斑测量时具有明确的物理意义—光斑能量中心,且在计算中使用了窗口范围内的全部灰度信息,理论上对于高频噪声具有很强的抗干扰能力,是目前应用最广的目标位置探测算法[1,16,17]。在缺乏曲线形状先验信息时,灰度质心法是现有算法中的最优选择,然而,在曲线背景存在干扰的情况下,尤其是干扰信号距质心较远时,计算结果容易产生较大偏差。因而通常采用窗口截取的方法来降低干扰信号的影响,但此时截取窗口的选取事实上决定了最终计算得到的质心位置,算法的稳健性严重依赖图像的预处理策略。
为解决背景干扰下曲线中心的稳健估计问题,提出了一种通用的拟合算法,采用将曲线与自身水平镜像匹配的方式,构造自变量为镜像翻转轴位置的对称性评价函数,采用最小二乘法,求取对称性评价函数极小值点,作为被测曲线的对称中心(symmetry center)。该方法无需了解被测曲线的近似数学形式,仅含有对称中心位置一个待求参数,且利用到了曲线与镜像重合部分的全部灰度信息,适用于多种形状的曲线中心拟合。
2 曲线对称中心拟合算法
2.1 算法的基本原理
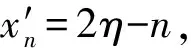
对原离散曲线进行插值,得到连续曲线:
y(x)=y⎣x」+(x-⎣x」)g⎣x」
(1)

=yn-[y⎣2η-n」+(2η-n-⎣2η-n」)g⎣2η-n」]
(2)
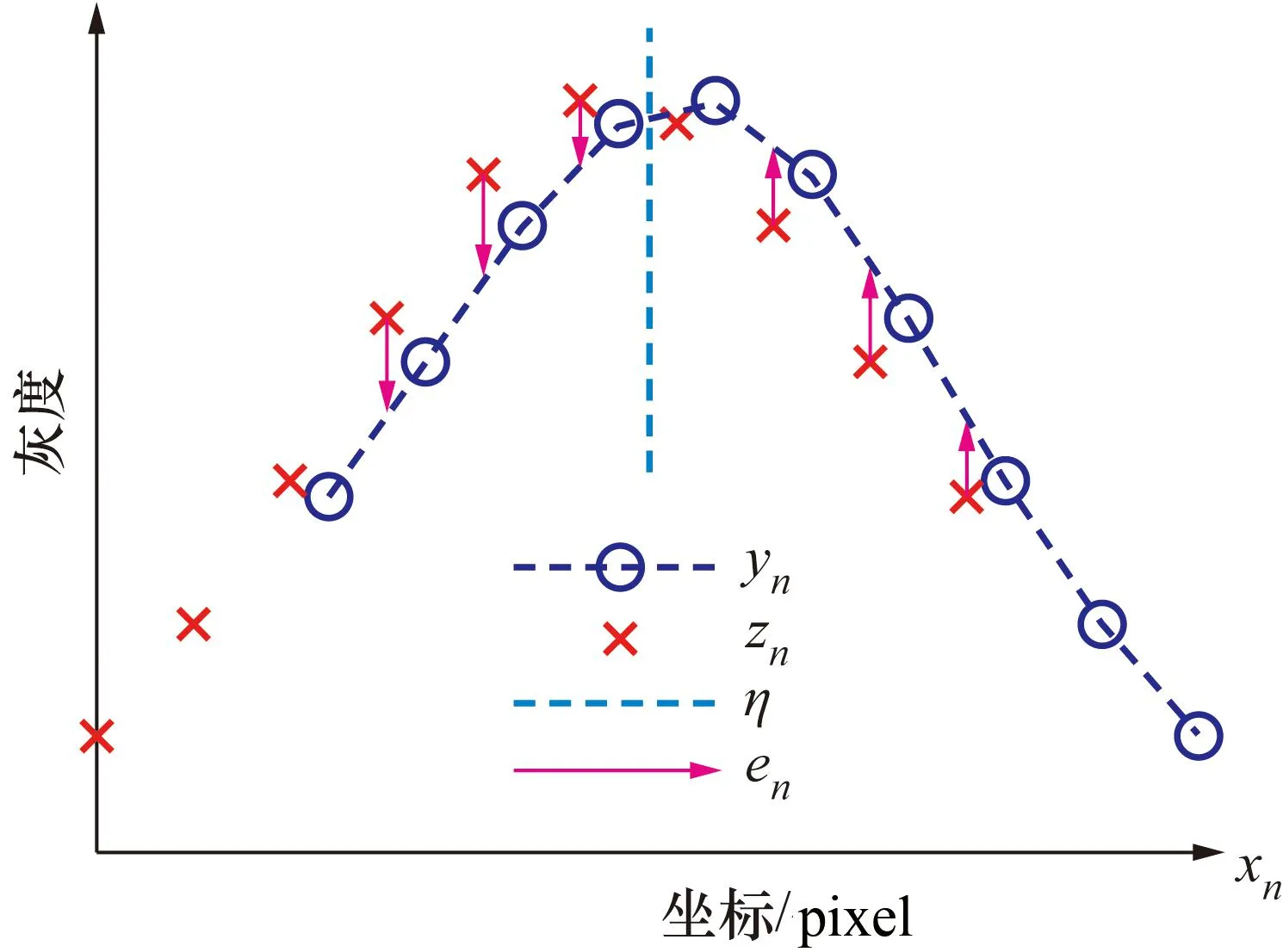
图1 曲线与其镜像进行匹配Fig.1 Match the curve to its mirror image
令η=η0+ξ,其中,η0=⎣2η」/2,显然,0≤ξ<0.5, ⎣2η-n」=⎣2η」-n=2η0-n,则有:
en=yn-{y2η0-n+[2η-n-(2η0-n)]g2η0-n}
=yn-y2η0-n-2ξ·g2η0-n
(3)
在已知η近似值的情况下,可以计算出η0。以所有点不重合误差的平方和作为对称性评价标准,可按式(4)构造对称性评价函数f(ζ)。
=∑(yn-y2η0-n-2ξ·g2η0-n)2
(4)
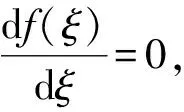
(5)
计算得到的对称中心位置即为η0+ζ。分析式(5)可知,无论是对曲线进行上下平移、垂直缩放或是上下颠倒(反色),对称中心的计算结果均不会受到影响。
2.2 迭代计算及收敛误差
在实际应用中,由于η和η0均未知,在使用式(5)计算计时,采用近似值ζ0代替η0,计算结果为:
(6)
可令ζ0=η0+k/2(其中k为未知整数),代入式(6)则有:
(7)
定义k范围内的平均梯度gn,k=(yn+k-yn)/k,有yn+k=yn+kgn,k,代入式(7),得:
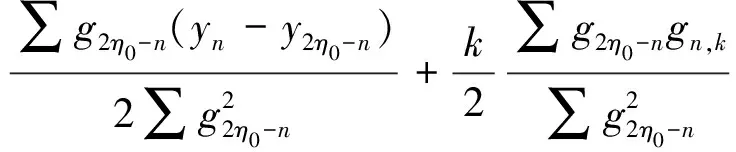
(8)

(9)
此时的对称中心计算结果为:
(10)
如采用迭代计算,将上1次计算得到的η′用于计算下1次的ζ0,则迭代结果收敛的充分必要条件为:
(11)
考虑到0≤ξ<0.5,可知:
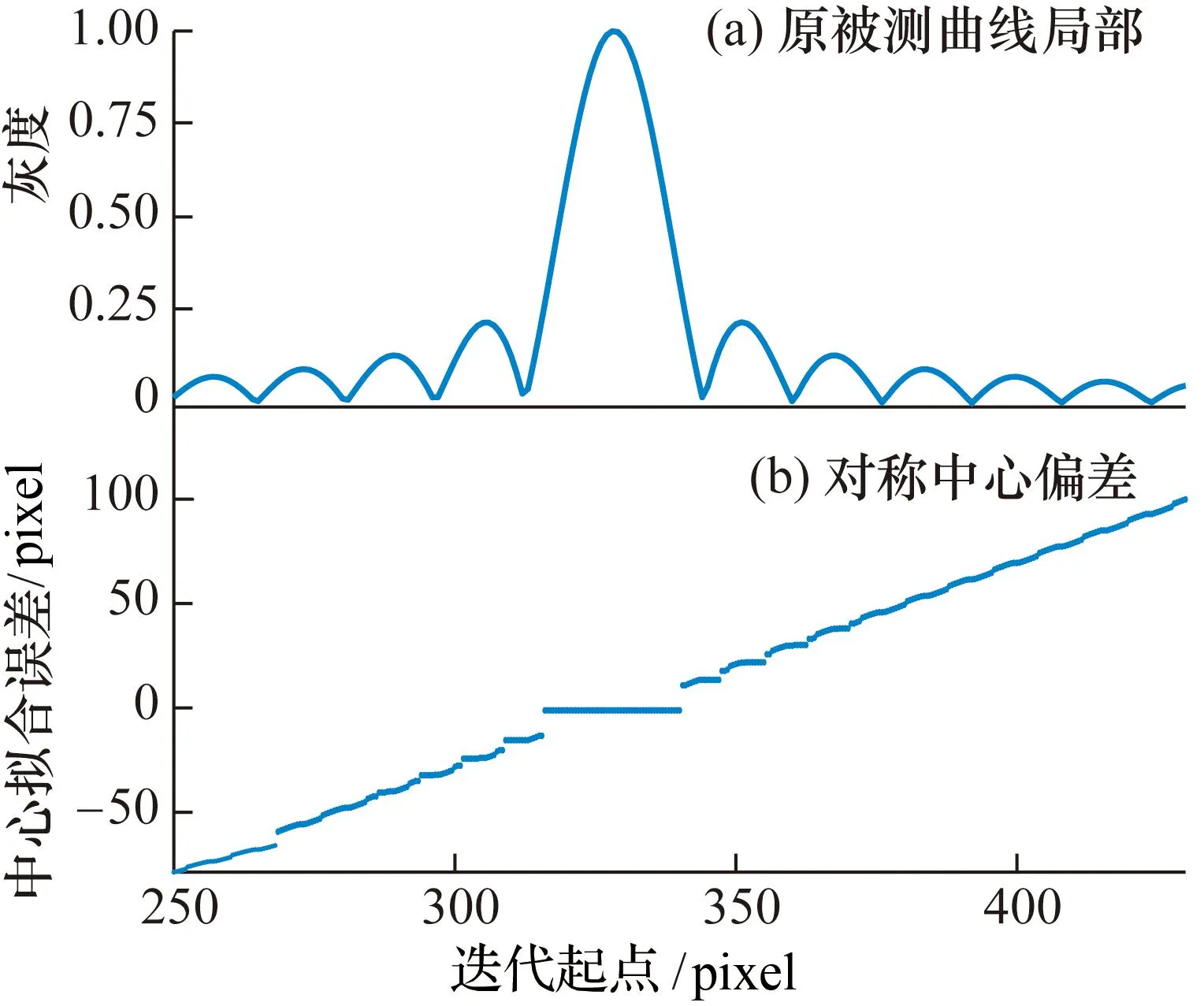
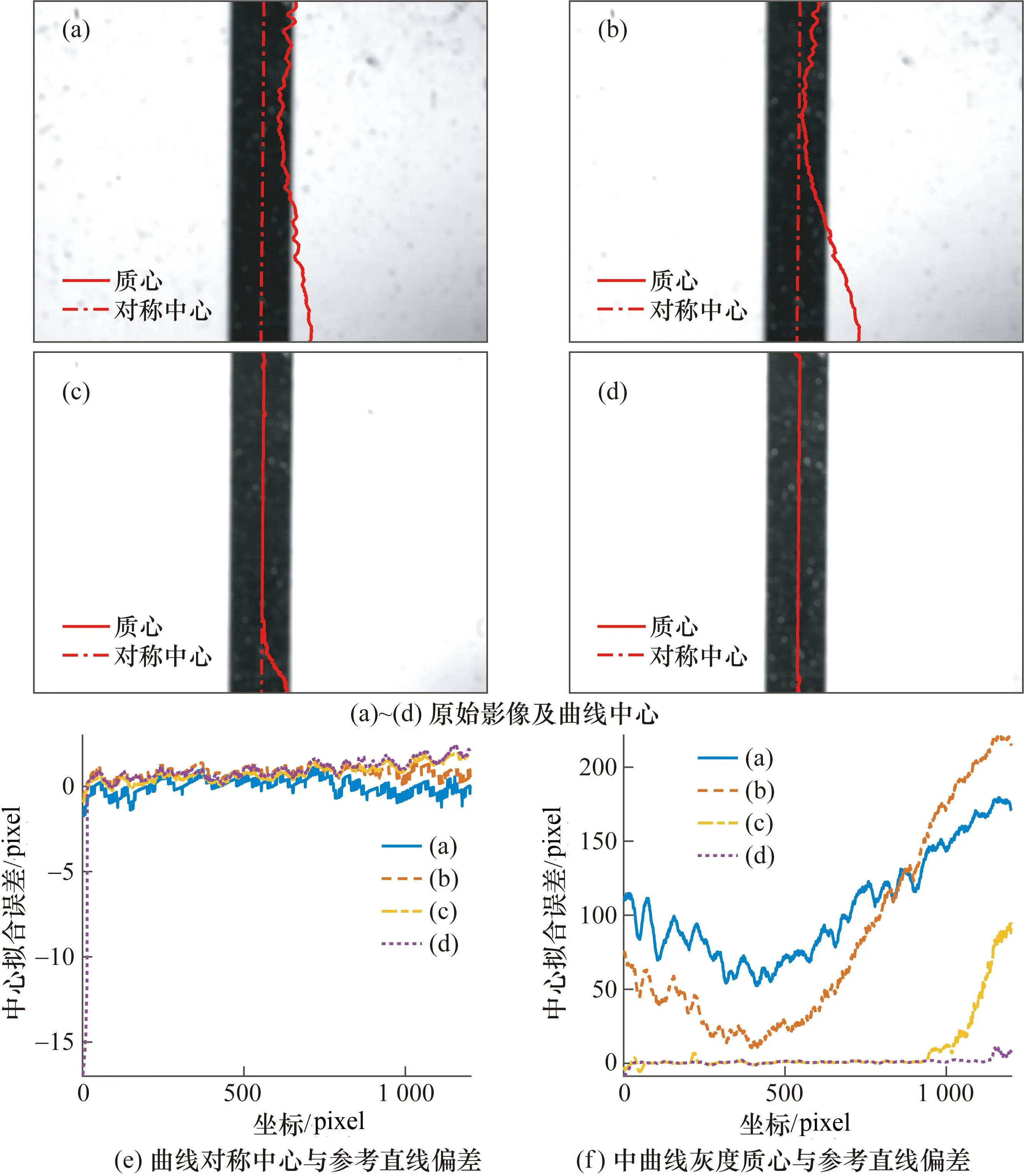
-1 (12) (13) 因此,可以认为,当迭代收敛时,k的值只有3种可能性:-1,0,1。根据式(9)及ζ、G的可能取值范围,可以得到k的取值与γ取值范围的相互关系。表1列出了k取不同值时,γ的可能取值范围,表2列出了γ在不同范围时,k可能的值。 表1 不同k值时γ的可能取值范围Tab.1 The possible interval of γ with different k value 表2 γ在不同区间时k可能的取值Tab.2 The possible k value when γ lies in different interval 可见,该算法有可能收敛至错误的对称中心,其原因在于式(3)仅在局部成线性,不能杜绝对称性评价函数出现多个局部极值的可能性。如果收敛结果出现错误(k≠0),只可能存在1种情况(见表2),以每0.5 pixel为单元格,实际的像素中心必然位于错误结果相邻的单元格内。因此,在迭代计算收敛后,仅需要在2种可能性中进行判定,即可避免收敛错误带来的影响。 (14) 迭代计算需要先预先得到对称中心的概略位置,如果算法对概略位置的精度要求过高,其适用范围将受到极大限制,在此,采用典型的多峰值曲线对算法迭代起点的收敛性能进行验证。 构造离散曲线yn=|sinc[π(n-328.33)/50]|,n=1,2,…,1000,其对称中心坐标真值为328.33,采用不同的迭代起算点计算该曲线的对称中心,结果与真值的偏差如图2所示。可见,对于对称中心拟合算法,只要迭代初始值选取在曲线主瓣范围内,即可保证收敛至正确的对称中心。 图2 迭代计算起点影响模拟实验结果Fig.2 Simulation results of different iterating start point 污点干扰是图像测量中常见的情况,通常来自杂散光斑、衍射条纹及测量光路中的灰尘等,其对曲线中心拟合结果的影响会随出现位置的不同而变化,在此对污点干扰的影响进行验证。 图3 污点干扰影响模拟结果Fig.3 Simulation results of spot interference 在理想的图像测量中,目标曲线的背景应当是均匀的,在灰度质心计算中,甚至要在整个图像中减去背景灰度值,以避免背景灰度影响。而在实际测量中,由于环境光、测量对像颜色不均匀或区域变色等因素影响,曲线可能存在不均匀背景,在此对不均匀背景的影响进行验证。 图4 不均匀背景影响模拟结果Fig.4 Simulation results of background interference 可见,不均匀背景对对称中心的影响远小于对灰度质心的影响,主要原因在于背景图像自身的灰度质心与原始图像质心不重合时,必然引起总体灰度质心朝向背景质心的偏移,而背景图像自身的对称性评价函数较为平坦,因而总体对称性评价函数极值点受其影响极为有限。 在通常的图像处理中,会设置1个截取窗口,以排除目标区域以外图像的影响,而截取窗口不同的选取方案,会造成曲线中心计算结果不同。在此分别对2种常用窗口截取方式造成的影响进行验证。 将最大灰度所在像素作为截取窗口中心,在区间[21,301]内改变窗口宽度,分别计算截取后曲线的灰度质心及对称中心,结果见图5。 图5 以最大灰度中心窗口截取影响模拟结果Fig.5 Simulation results of cut out curve with max-gray-scale-center window 设置阈值t∈[0.5, 1.5],删去被测曲线中灰度小于t的部分,并删去剩余曲线中与主峰断开部分,分别计算截取后曲线的灰度质心及对称中心,结果见图6。由图6可见,对于较为复杂的非对称曲线,对称中心受截取窗口选择的影响远小于灰度质心。 图6 阈值窗口截取影响模拟结果Fig.6 Simulation results of cut out curve by gray scale threshold 采用工业相机及1倍远心镜头,对准条码水准标尺中的1根条码(黑色),保持相机与条码固定不动,在均匀照明的基础上,在侧方设置强光源,以产生不均匀背景。使用工业相机采集图像,图像的每1行作为独立的灰度曲线,采用对称中心拟合算法直接计算对称中心,同时,对每一曲线进行反色处理(用饱和灰度值减去图像灰度值),计算每一反色曲线的灰度质心。 图7展示了其中1帧图像的各行曲线中心计算结果。灰度质心的连线由于条码内、外的污点而产生了明显的扭曲,而图像右下角的暗色区域使得灰度质心明显偏离条码中心;与之相比,曲线对称中心连线基本不受污点与背景的干扰,在条码中心附近,成一条与条码平行的近似直线。 图7 实际图像中的曲线中心拟合结果Fig.7 Curve centers in real photo 通过调节光照强度,获取不同曝光度的测量影像,采用对称中心拟合算法及灰度质心法计算图像中每行的对称中心及灰度质心,并与参考直线x=814.16-0.0089565y(由其中一帧图像对称中心拟合得到,坐标系原点在左上角,y方向朝下为正)相比较,其结果见图8,其中图8(a)~图8(d)分别是曝光度依次增大的影像,图8(d)曝光度最大,背景噪声最少。在曝光度发生巨大变化的情况下,每行灰度曲线的对称中心变化量绝大部分在像素量级(在图8(d)中,条码右上角的亮斑扩大,覆盖了右边缘,使得前14行灰度曲线中心向左移动了11~16 pixel),而灰度质心受背景图像的影响,位置变化量达到了数十甚至上百像素。 图8 不同曝光度所得图像每行曲线中心Fig.8 Curve centers obtained with different exposures 表3列出了图8(a)、图8(b)、图8(c)中每行(除去图像前14行数据)灰度曲线对称中心与图8(d)中对称中心位置之差均方根值(RMS)。 表3 对称中心位置变化量均方根值Tab.3 Table 3 RMS of symmetry center change 提出了一种通用的曲线中心拟合算法,通过曲线与其镜像匹配程度,构造对称性评价函数,定义了对称性评价函数最小值点为曲线的对称中心。通过构造对称性评价函数,实现了曲线对称中心的定义,推导出曲线对称中心的计算公式,并对迭代计算的收敛情况进行了分析,给出了收敛结果的判定方法。对称中心拟合算法经过理论分析及模拟、实际验证,不受曲线上下平移、缩放与翻转的影响,与灰度质心法相比,对污点及不均匀背景具有极强的抗干扰性,受窗口截取的影响也远小于灰度质心,是一种稳健的拟合算法,在实际使用中,对图像预处理的要求较低,具有普遍的适用性。且对称中心拟合算法不仅适用于图像处理中的曲线中心计算,也可应用于其他领域(比如时域信号分析、光谱分析等)。 在实际应用中,可以针对被测图像特点,对算法实施进一步改进,比如梯度计算中可以采用平均梯度,以减小高频噪声的影响,或者引入加权策略,增加重要特征的权重等。 目前尚未对算法所能达到的最高精度进行验证,后续将结合具体应用,对其计算精度进行进一步验证与评价,同时,还将对算法向二维图像中心拟合进行扩展,用于对称轴(轴对称)或对称中心(中心对称)的计算。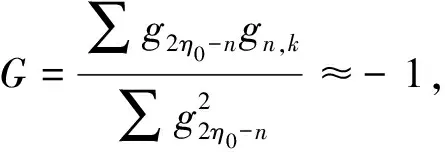


2.3 迭代计算结果的判定
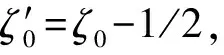
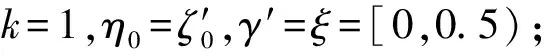

3 算法的模拟验证
3.1 迭代起点与收敛性
3.2 污点干扰的影响
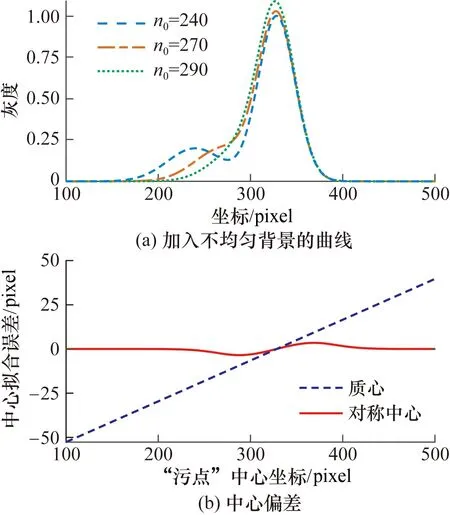
3.3 不均匀背景的影响
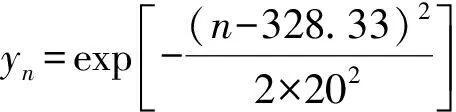

3.4 截取窗口的影响


4 算法的模拟验证


5 结 论
