基于贝叶斯动态模型的激光干涉仪漂移误差预测

刘丽颖, 程真英, 陈 旭, 李瑞君

( 合肥工业大学 仪器科学与光电工程学院 测量理论与精密仪器安徽省重点实验室，安徽 合肥 230009)

1 引 言

漂移是测量系统的重要性能指标之一,其好坏直接影响测量系统的测量精度。激光干涉仪因其具有大测量范围、高分辨力、高测量精度和直接溯源至激光波长等优点被广泛应用于高精度位移测量领域[1～3]。然而,激光干涉仪在实际测量中受到温度波动、气流扰动、振动等外界环境因素以及激光器自身因素的影响,其测量结果随测量时间会产生较大的漂移误差,从而导致系统测量精度下降[4,5]。

近年来,国内外许多学者在漂移误差抑制与补偿方面进行了相关研究: 1) 利用高精度的恒温控制箱可以降低温度波动对测量系统结构和空气折射率的影响,该方法操作简单,能够有效提高系统的测量精度,但其存在体积大、成本高、不易搬运等缺点[6～9]; 2) 采用诸如花岗岩、微晶玻璃等具有低热膨胀系数的材料搭建测量系统的基座或框架可以减小测量系统受环境温度引起的结构变形,进而降低结构变形引起的漂移误差,但材料本身造价较高,对稍微复杂一些的结构更是难以加工[10,11]; 3)通过合理的结构设计可以降低漂移误差对测量系统精度的影响,但该方法设计阶段耗时较长且随着系统结构的繁复程度有所增加[12～14]。此外,陶盼等人提出了一种利用波纹管和气泵使空气折射率均匀化的方法,使激光测量系统的光束稳定性提高50%[15]。Tao等提出了一种扫频光纤干涉仪的漂移误差补偿方法,光路长度漂移误差由共享光纤光路的光纤迈克尔逊干涉仪实时监测进而实现误差补偿[16]。Kuang等采用激光与单模光纤耦合的方式减少了激光光源引起的漂移误差[17]。以上方法从测量系统设计的角度出发,最大限度提高系统结构的稳定性,削弱系统本身对环境的敏感性,减少漂移误差的产生。然而,高精度的环境控制在实际测量中成本高昂,结构设计耗时长且不易实现。

相较于上述方法,采用软件技术进行漂移误差补偿的方法具有成本低、实时性好、通用性强的特点,并且无需额外增加测量系统的体积。常用的漂移误差补偿方法有:多项式拟合[18]、小波分析[19]、时间序列分析[20,21]、神经网络建模[22,23]、支持向量机[24]等。Plotkin等采用多项式拟合方法补偿了正交磁通门传感器的温度漂移误差,该方法易于实现、便于集成,但补偿精度较低[18]。Song等提出一种基于稀疏冗余表示的小波降噪方法,降噪后MEMS陀螺仪残余随机漂移误差的标准差为0.014 7°/s[19]。在小波降噪的基础上,李光耀等提出基于粒子群优化BP神经网络的光纤陀螺温度漂移补偿方法,补偿后光纤陀螺在不同温度下输出标准差降低了60.19%[22]。小波分析方法中选择合适的小波基函数和阈值十分困难;而神经网络需要大量的数据样本进行模型训练,且容易产生过拟合、局部极小等问题。Narasimhappa等采用基于时间序列模型的自适应无迹衰退卡尔曼滤波方法减少了光纤陀螺漂移,建立时间序列模型需要对数据进行平稳化处理[21]。杨遂军等提出了一种基于最小二乘支持向量机的硅压阻式传感器温度补偿模型,在0～400 ℃温度范围内综合精度由3.2%提高到0.25%,该方法需要人为选择惩罚系数和核函数[24]。

在实际测量中,激光干涉仪系统所处的测量环境复杂多变,一方面使得高精度的环境控制难以保证,另一方面使得硬件结构设计所能达到的漂移抑制效果有限。因此,如何依据系统的测量过程实现系统的实时漂移补偿显得尤为重要。此外,激光干涉仪输出的位移信号中既包含真实测量数据又包含漂移误差,且漂移误差的初始状态一般无法预知。因此,如何充分利用非测量阶段采集得到的漂移数据建立相应的跟踪预测模型,是实时补偿激光干涉仪漂移误差的关键。

本文引入基于无信息先验分布的贝叶斯动态模型来建立激光干涉仪的跟踪预测模型。分析了迈克尔逊激光干涉仪漂移误差特点;基于贝叶斯动态模型建立了合理的预测模型结构;利用无信息先验分布法得到了漂移误差的初始信息,而后基于贝叶斯递推算法估计了模型状态参数;根据预测模型实现了干涉仪漂移误差的预测;通过实验验证了该方法的正确性和有效性。

2 基于无信息先验分布的贝叶斯动态模型及其预测原理

2.1 贝叶斯动态模型及其预测原理

建立动态模型是贝叶斯预测的基础。激光干涉仪的漂移误差序列在大多数情况下是随时间变化的非平稳随机序列,其特征主要表现为线性、周期性和随机性,因此可以采用具有多种模型结构的贝叶斯动态线性模型进行描述。模型中状态方程与观测方程分别为:

Xk=AkXk-1+Wk

(1)

yk=CkXk+Vk

(2)

式中:k为离散时间;Xk为k时刻的状态向量;Wk为状态噪声;yk为k时刻的漂移误差信号;Vk为一维的观测噪声,且Wk与Vk相互独立;Ak为状态转移矩阵;Ck为观测矩阵。若Xk和Wk为s维矩阵,则Ak和Ck的矩阵大小分别为s×s和1×s。

设D0为k=0时初始信息的集合,Dk表示k时刻及其以前时刻所有有效信息的集合。假设状态向量、状态噪声和观测噪声的初始先验分布均服从正态分布,即(X0|D0)～N(m0,c0),Wk～N(0,wk),Vk～N(0,v),由式(1)可以得到k(k≥1)时刻状态向量Xk的先验分布密度函数:

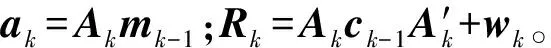
(3)

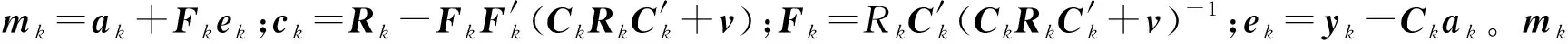
2.2 无信息先验分布法

在实际测量中,由于激光干涉仪的漂移误差具有随机性,使得递推所需的状态初始分布和噪声先验分布不易获得。因此,引入无信息先验法以获得递推所需初始信息。

上述模型中有s+1个参数(包括v),需要至少观测s+1次来得到合适的后验分布。在确定初始信息阶段采用的观测数据较少,无法估计出参数的任何变化,因此可设wk=0(k=1,2,…,s+1)。假设初始先验分布密度p(X1,v|D0)∝v-1。经推导可得Xk和v(k=1,2,…,s+1)的联合先验和后验分布密度函数[25]:

对联合后验分布密度函数进行整理可得:

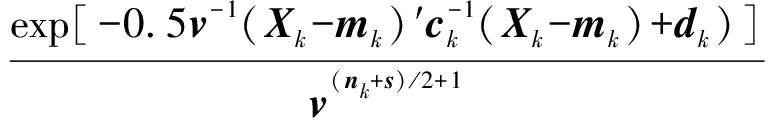
(4)

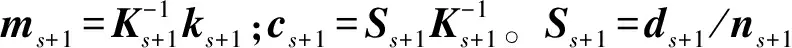
当k>s+1时,将式(4)对v进行积分可以得到k时刻Xk的后验分布密度函数:

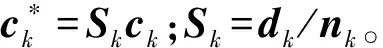
p(Xk-1|Dk-1)∝

p(Xk|Dk-1)∝

p(yk|Dk-1)∝

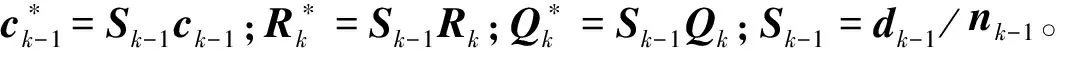
(5)

综上,可以得到基于无信息先验分布的贝叶斯递推算法如下所示。

初始化

H1=Os×s,h1=Os×1,λ1=0,r0=0

fork=1:s+1

end

fork>s+1

end

3 激光干涉仪的漂移误差预测

FAN K C等研制了基于迈克尔逊干涉原理的激光干涉仪,可用于微/纳米测量探头和微纳米三坐标测量机上[26]。在此基础上,采用对称式结构设计减小了结构热变形并采用优化设计电路减小了干涉仪的非线性误差,但其在实际测量中仍存在较大的漂移误差[27]。为进一步提高该干涉仪的测量精度,减小其漂移误差是亟需解决的问题。

3.1 迈克尔逊激光干涉仪原理及装置

迈克尔逊激光干涉仪的工作原理如图1所示。激光光源LC发出的部分偏振光经过偏振分光棱镜PBS1分为透射光P光和反射光S光,两束光分别经过1/4波片QWP1、QWP2而后被测量镜MM和参考镜RM反射。两束反射光再次经过QWP1、QWP2,使得原来的P光转化为S光、原来的S光转化为P光。由于光线的透射和反射状态发生变化,两束光经反射不会原路返回激光器,而是进入QWP3。QWP3使重合后的两束光产生干涉,消偏振分光棱镜NPBS、PBS2和PBS3构成鉴相模块用于获取4路相位差为90°的光强信号,并由光电探测器PD1-PD4检测。

实验装置如图2所示。光源为532 nm波长的固体激光器(长春新产业有限公司,型号:MSL-III-532 nm)。配套光学器件由厂家根据波长定制,底板及支座均采用因瓦合金(线膨胀系数α:1.5×10-6/℃)加工而成。干涉仪的输出位移信号由16位的数据采集卡(美国NI,型号:NI-6259)采集。

图2 实验装置图Fig.2 Experimental setup

3.2 漂移误差分析与建模

为实现激光干涉仪的漂移误差建模预测,首先要了解分析漂移误差的特征和变化规律,建立符合其变化规律的模型。将第3.1节描述的激光干涉仪置于恒温计量实验室中(温度:20 ℃±0.5 ℃,相对湿度:50%±5%),调整参考反射镜RM使干涉仪的输出信号为零。测量反射镜MM支座在光轴方向上的长度为7 mm,由热变形伸长量计算公式ΔL=αL(T2-T1)可知,其在光轴方向上总体伸长量为±5.25 nm。由于支座受热变形向两个方向伸长,输入量的实际变化量为±2.625 nm,与漂移误差相比可以忽略不计。

为了降低激光器预热和人为调整干预的影响,实验前激光器开启1 h,并保持周围安静。而后利用数据采集卡记录非测量阶段输出位移的漂移误差数据。考虑到大多数位移测量实验可以在1 h内结束,以及预测模型建立需要一段漂移误差数据,因此采集2 h的漂移误差数据用于建模预测。在相同实验条件下,连续6次记录的漂移误差曲线如图3所示。采样频率设置为1 Hz。

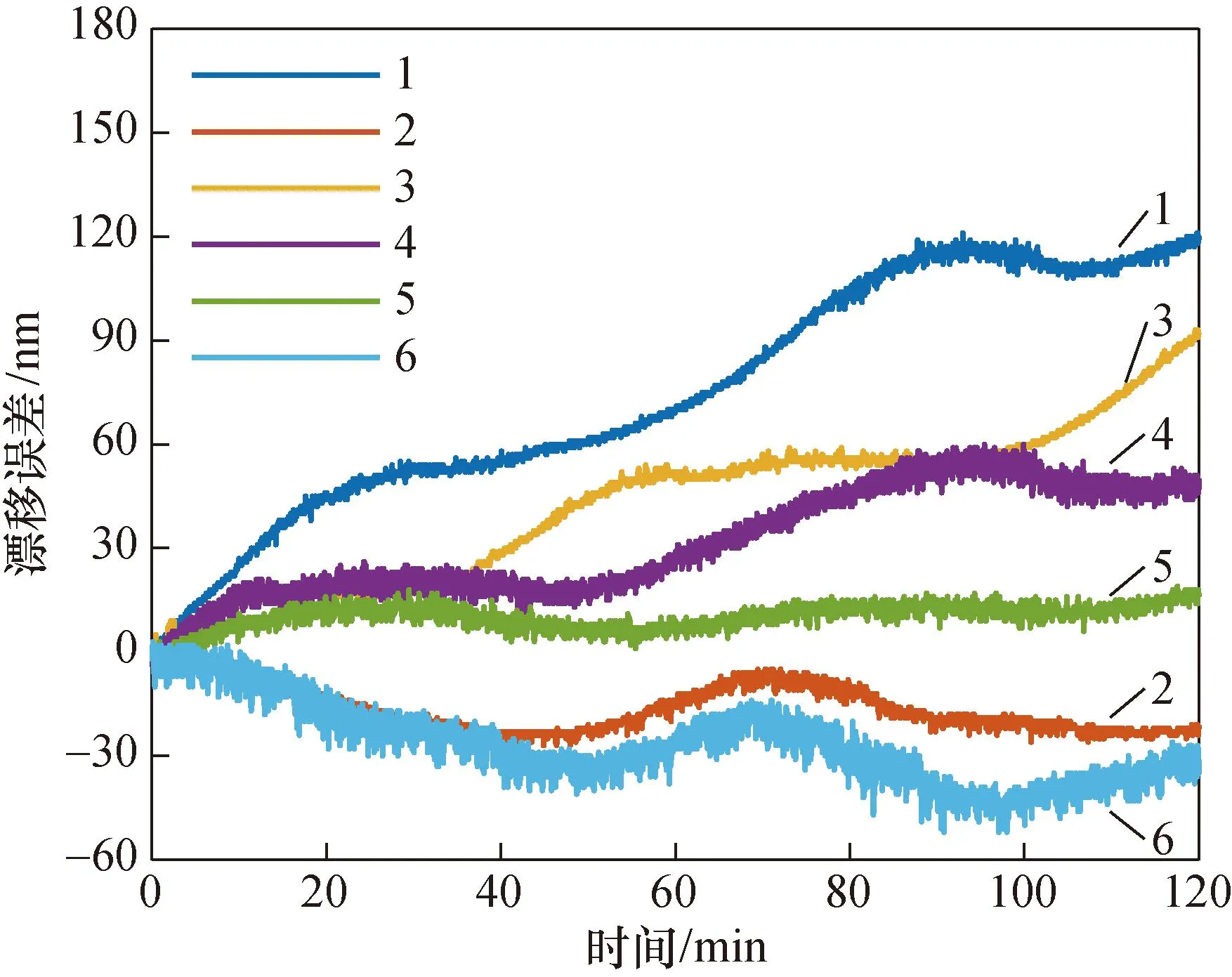
图3 迈克尔逊干涉仪的漂移误差数据Fig.3 Drift error data of Michelson interferometer

从图3可以看出:激光干涉仪在持续工作2 h内,漂移误差序列的变化规律主要表现为线性和周期性。此外,还具有一定的随机性。在长时间工作过程中,外界控温环境的温度波动以及激光器自身产热使得系统内部温度变化,而温度变化引起的机械变形、光路干扰等因素会使得漂移误差序列呈现线性增长和周期性波动。从图3还可以看出:虽然6次重复漂移实验结果的总体规律特性是一致的,但漂移实验的重复性并不好。说明漂移误差具有较大的随机性。因此,在综合考虑漂移误差规律的同时,还需要对其进行实时监测,从而才能建立激光干涉仪精确的漂移误差预测模型。

贝叶斯动态模型具有多种模型结构,如周期模型、回归模型、多项式模型、噪声模型等,这些模型还可以依照叠加原理进行叠加,故而非常适合建立包含线性成分、周期成分及随机成分的误差精确预测模型。根据激光干涉仪漂移误差的特点,采用贝叶斯线性回归分量模型和周期分量模型组合构建预测模型。

贝叶斯线性回归模型可以表示为:

式中:[akbk]′为状态变量;ak和bk分别表示线性规律的斜率和截距。相应的矩阵参数为:

(11)

周期模型可以表示为:

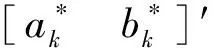
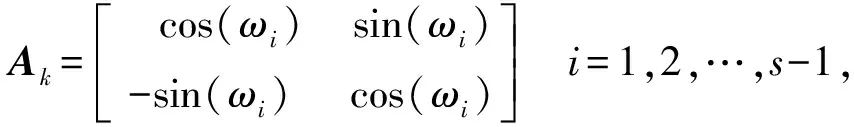
(12)

式中:ω=2π/T,T为误差序列周期分量中每个周期的采样点数。当T为奇数时,认为误差序列由s=(T+1)/2个调和分量和水平分量组成,当T为偶数时,认为误差序列由s=T/2个调和分量和水平分量组成。周期模型分量的个数i需要根据实际测得漂移信号的频谱分析结果进行确定。

由于线性模型叠加后仍是线性模型,叠加原理也适用于贝叶斯动态线性模型。激光干涉仪的漂移误差序列主要呈现线性和周期性,因此采用1个线性回归分量模型和i个周期分量模型叠加对其进行描述。叠加得到的组合模型为:

状态转移矩阵:Ak=diag[A1k,A2k,…,Ajk]

观测矩阵:Ck=[C1k,C2k,…,Cjk]

其中:diag(·)为对角矩阵,j=1,2,…,i+1。

3.3 漂移误差预测补偿流程

基于上述构建的预测模型,利用无信息先验分布的贝叶斯递推算法对模型参数进行递推估计,而后将预测模型计算的结果作为补偿量,对激光干涉仪输出位移信号进行漂移误差补偿(在激光干涉仪原始输出的漂移信号上减去模型的预测值)。漂移误差预测补偿的流程图如图4所示。

图4 漂移误差预测补偿流程图Fig.4 Flowchart of the drift error prediction and compensation

4 实验与分析

4.1 漂移误差数据特性分析及预测

开机预热1 h后,非测量阶段采集的漂移误差曲线如图3所示。因为大多数位移测量实验可以在1 h内结束,所以将图3中60～120 min的漂移误差数据作为预测集,用于验证预测效果。同时,将0～60 min漂移误差数据作为训练集,用于估计预测模型中状态参数。针对第1次激光干涉仪漂移误差数据,对训练集数据序列去除线性趋势后,采用非线性最小二乘拟合得到了残余误差的角频率(R2=0.981),ω1=0.002 153,ω2=0.002 172。因此,采用一个回归分量模型和两个周期分量模型来构建预测模型。依据叠加原理,预测模型结构如下所示:

(13)

Yk=[k1 1 0]Xk+Vk

(14)

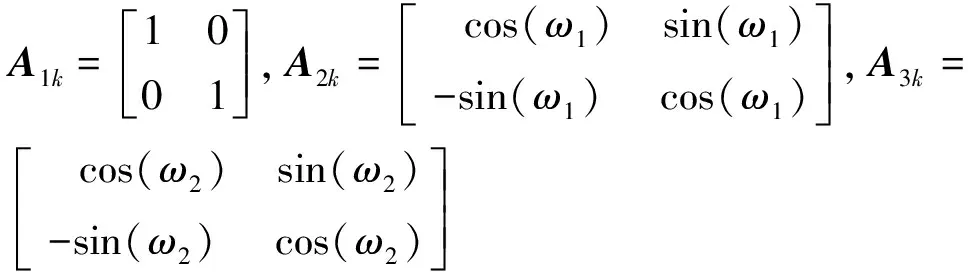
基于上述预测模型结构和训练集数据,利用第2.2节基于无信息先验分布的贝叶斯递推算法估计了模型状态参数:

利用最终的预测模型迭代递推得到的漂移误差的预测曲线如图5所示。

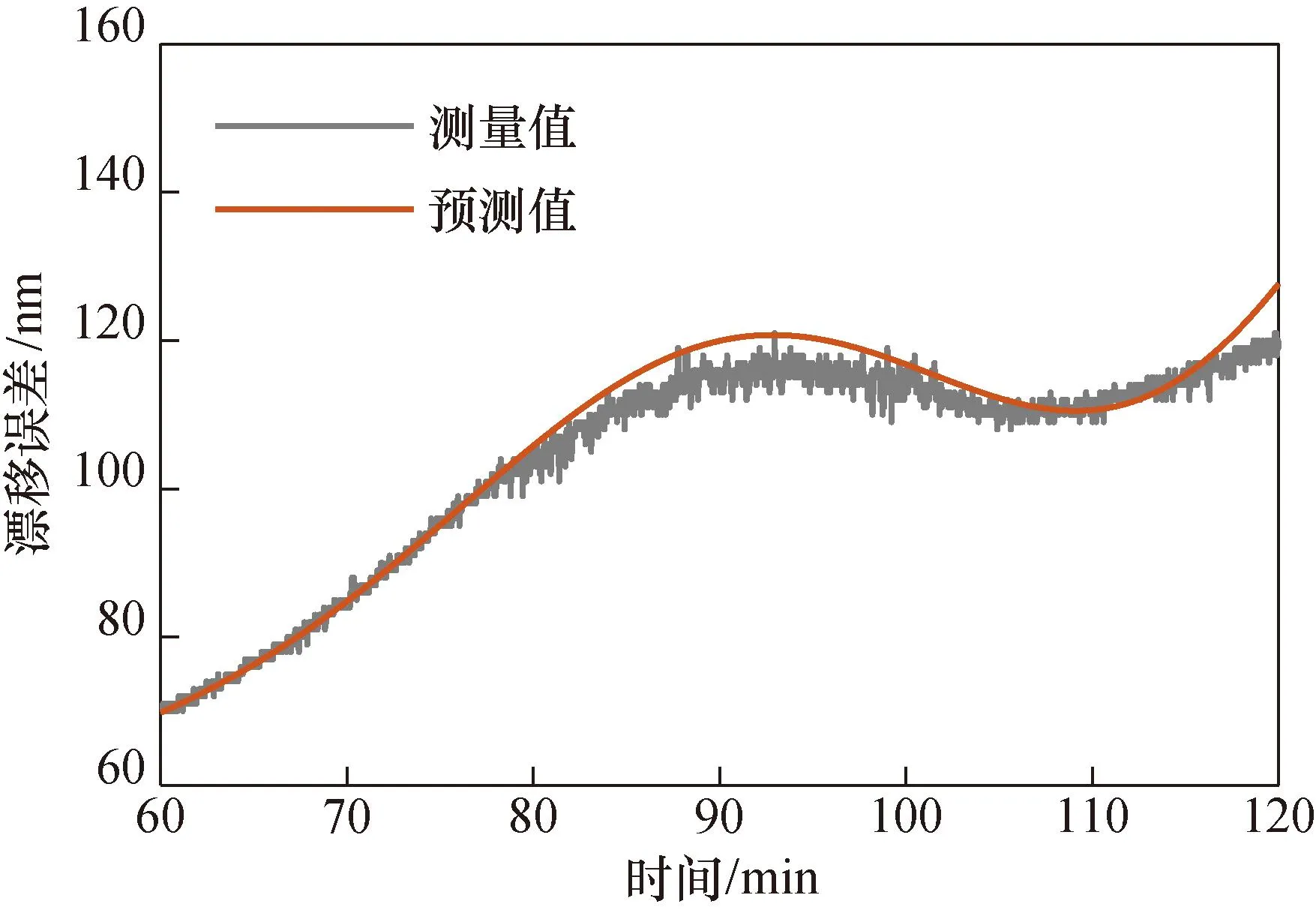
图5 贝叶斯动态模型的预测结果Fig.5 Prediction of Bayesian dynamic model

从图5可以看出:在整个预测集数据段内,预测漂移误差曲线与实际漂移误差曲线趋势相近,漂移误差的均方差(mean square error,MSE)减小了99.93%(由1.10×104nm2减小到8.25 nm2)。此外,漂移误差的变化量减小了75.98%(由51 nm减小到12.25 nm),说明文中提出的方法能够实现漂移误差的预测补偿。

4.2 分析与讨论

4.2.1 与常用建模方法预测效果的比较

为验证文中方法对漂移误差预测补偿的有效性,将其与最小二乘拟合建模预测方法和神经网络建模预测方法进行了比较。最小二乘拟合模型和神经网络模型利用MATLAB拟合工具箱和神经网络拟合工具箱训练获得。采用3种方法预测得到的漂移误差曲线如图6所示。

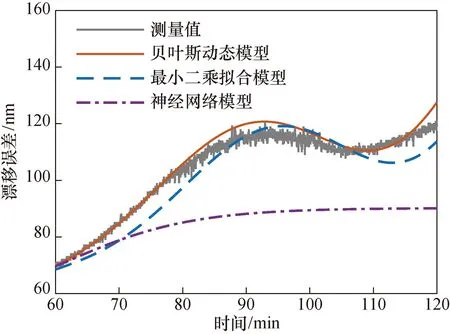
图6 3种模型的预测结果Fig.6 Prediction results of three models

从图6可以看出:采用神经网络模型预测的漂移误差不能很好地反映实际漂移误差的周期性规律。在整个预测集数据段内,通过拟合模型预测补偿后的MSE为26.66 nm2,通过神经网络模型预测补偿后的MSE为429.78 nm2。与上述两种方法相比,采用文中方法预测补偿后的MSE分别减小了67.85%和99.08%,说明基于贝叶斯动态模型的漂移误差预测补偿方法比其他两种预测补偿方法更有效。

4.2.2 训练集长度对预测效果的影响

训练集长度不同会对预测补偿效果产生影响。针对第1次漂移实验数据,分别采用4种不同长度的数据作为训练集,即50、60、70、80 min,而后采用文中方法预测漂移误差,漂移预测曲线如图7所示,80～120 min残余误差的MSE如表1所示。

表1 残余误差MSE比较Tab.1 Comparison of residual error’s MSE nm2

图7 预测结果比较Fig.7 Comparison of prediction result

从图7和表1可以看出:采用50 min训练集预测的趋势与实际漂移趋势有偏差,其余3种长度训练集的预测曲线基本重合,且在80～120 min内残余误差的MSE相差不大。考虑到训练集长度不宜过长,因而选取60 min长度的训练集对漂移误差数据进行预测。

4.2.3 稳健性验证

对图3中漂移误差序列进行预测补偿,补偿前后残余误差的MSE如表2所示。

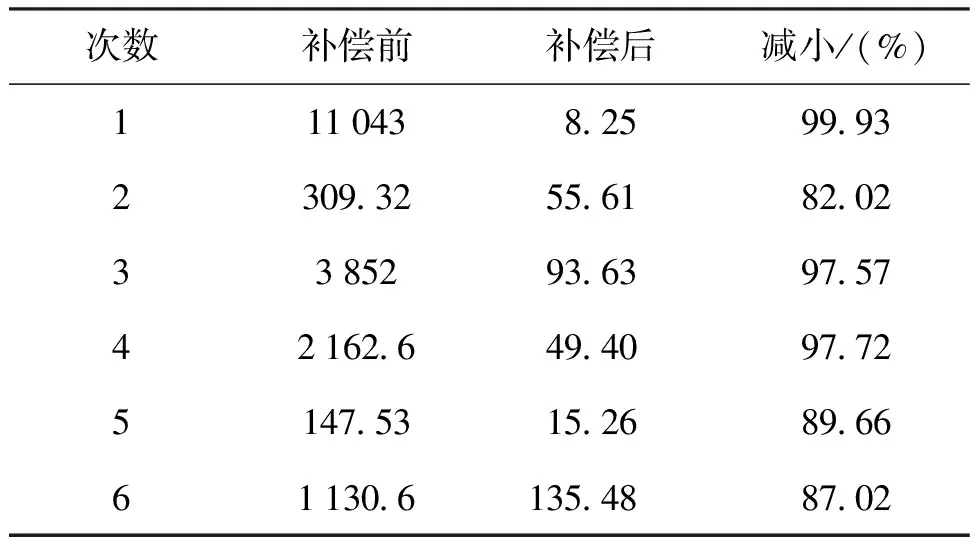
表2 补偿后的残余误差Tab.2 Residual error after compensation nm2

从表2可以看出:6次重复性实验漂移误差预测补偿后的MSE均减小了82%以上,验证了文中方法的稳健性。

5 结 论

提出了一种用于激光干涉仪漂移误差预测补偿的方法,建立了基于贝叶斯动态模型的预测模型框架,利用基于无信息先验分布的贝叶斯递推算法估计了模型状态参数,实现了激光干涉仪漂移误差预测补偿。实验结果表明:1) 与拟合预测方法和神经网络建模预测方法相比,采用文中方法预测补偿后的MSE分别减小了67.85%和99.08%,且文中提出的方法能更好地预测漂移趋势;2) 针对自制激光干涉仪的漂移误差数据,采用60 min及以上的数据进行训练,均可达到较好的补偿效果;3) 6次重复性实验中漂移误差预测补偿后的MSE均减小了82%以上,验证了文中方法的稳健性。本文提出的漂移误差预测补偿方法不局限于激光干涉仪,亦可用于其他高精度的测量仪器。