声源定位算法反馈机制的引入

周龙杰， 赵思屹， 马洪宇

（武汉大学物理科学与技术学院，武汉 430072）

0 引 言

声源定位是指通过探测器探测声源发出的声波反向追溯声源的位置。声源定位系统不同于雷达等主动声呐系统，其不主动发出声波，属于一种被动声呐系统。随着科技的发展，越来越多的领域需要用到声源定位：军事［1-2］、视频会议［3］、机器人搜救［4］和故障排除［5］等。

通常有两种方法实现声源定位：可控功率响应法［6］（Steered response power，SRP）、基于时延估计定位法［7］（Time delay of arrival，TDOA）。这两者均需要用到不同几何形状的麦克风阵列（线阵、面阵，体阵），对录制到的音频使用不同的算法估计时延。不同的是，前者属于直接定位方法，需要对待测空间的功率响应进行全局搜索，峰值位置即为估计出的声源位置。后者属于两步间接定位法，在估计出时延后，结合麦克风阵列的几何分布求解非线性双曲方程组或者求解四维空间中的超锥拟合问题［8］来估计声源位置。

在间接定位中时延估计的准确性将直接影响声源定位的结果，如何准确估计时延是该类定位问题的重中之重。通常在其他条件不变的情况下，麦克风数量越多［9］、用于计算的音频越长［10］得到的估计结果越准确。在实时定位系统中，不可能一味地增加麦克风数量和增长单次录制的音频长度，需要在有限的麦克风数和音频长度中得到准确的估计结果。现有的研究大多数都集中在提出更有效的定位方法，使定位系统具有较高的抗噪、抗混响以及准确定位的性能。改进定位方法费时费力且针对性过强不具有普适性。如能在时延估计算法中提出一种普适的反馈机制，使得系统在估计出时延之后自动评估结果的合理性，则可更简单地提高定位方法的抗噪性、抗混响性和稳定性。本文结合麦克风阵列的几何分布，在时延估计过程中提出简单普适的反馈机制，并将其运用在二维平面内的五元十字麦克风阵列定位的情形下。在Matlab 编译环境下进行实验仿真，搭建一套线下定位系统付诸实践。

1 时延估计算法及反馈机制

1.1 基于广义互相关函数的时延估计

以距离为d的一对麦克风为例（见图1（a）），其中一个麦克风接收到的声音信号

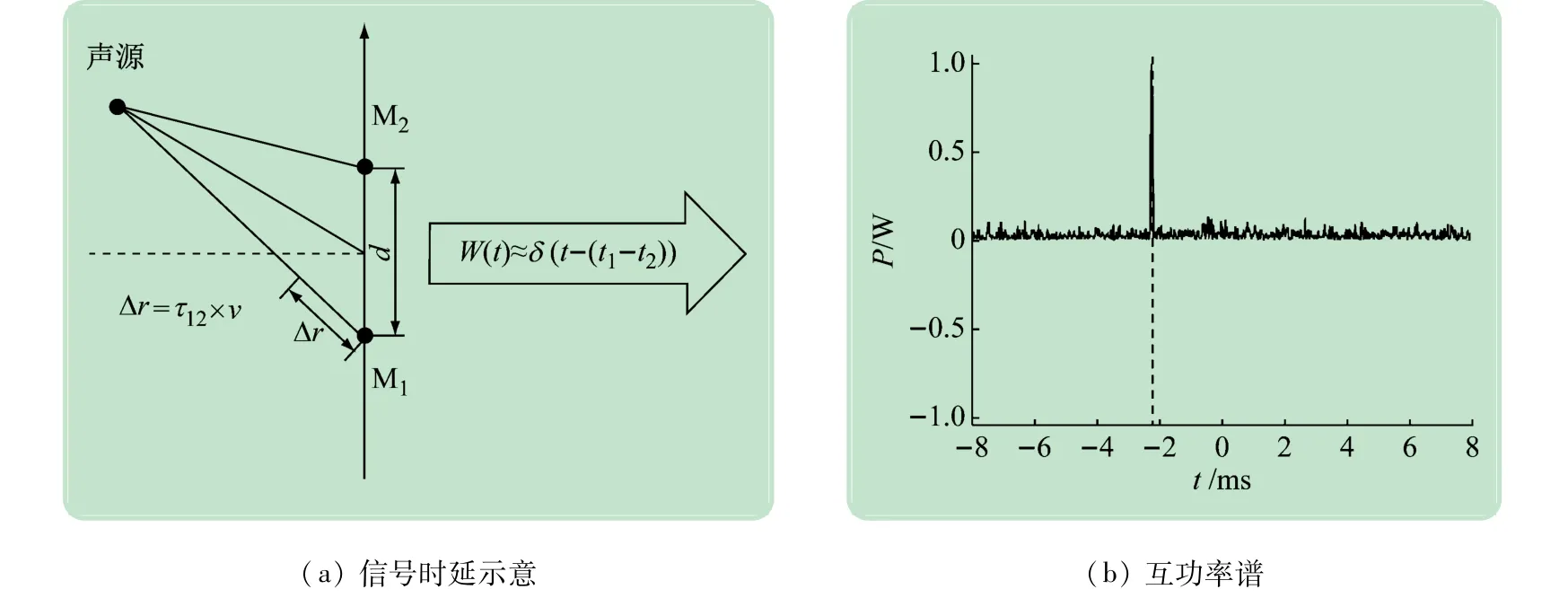
图1 基于广义互相函数的时延估计

式中：αn为衰减系数；Nn为线性无关的高斯白噪声；tn为声音信号传到n号麦克风所需时间（n＝1，2）；S（t）为声源信号。所以到达两麦克风的时延τ12＝t1－t2。对信号进行傅里叶变换

定义广义互相关函数

式中：G＝X1（ω）X*2（ω）；φ为加权函数，最常用的是phat加权函数，能够起到锐化峰值的作用［11］。

在弱混响的情况下，式（3）可以近似为：

W（t）可近似地看成δ 函数，且当t＝τ12时，W（t）取最大值。因此，可通过计算两段音频的互相关函数求得互功率谱，互功率谱峰值对应的值即为时延的估计值（见图1（b））。

1.2 反馈机制

传统时延估计方法通常只是对信号的互功率谱寻峰估计，并不能立即判断估计值的正确性。现实生活中声音信号复杂多变，可能在某一次估计的时候噪声过大，导致传统定位算法难以得到准确结果。如能引入一个反馈机制，使得定位系统能在估计出时延后及时判断并跳过噪声过大导致定位不准确的片段，则可大大提高定位结果的准确率。

对于拥有n个麦克风的阵列，具有一定的几何分布，估计来的Num ＝个时延之间存在确定的内在联系。因此可基于这一内在联系，设计一个反馈机制检验该次时延估计的合理性，提高时延估计的准确性。

通常时延分布有以下特性：

（1）时延存在最值。对于任意2 个相距d的麦克风M1、M2，如果已知声音信号到达2 麦克风的时延为τ12，则可计算声源到2 个麦克风的距离差Δr（见图1（a））。对于同一组麦克风（M1，M2），时延相等的声源位置是双曲线的一支（见图2），其中时延在2 麦克风连线的外侧上取到最大值τmax＝d／v（v为声速）、在2麦克风的垂直平分线上时延为0 s。由于麦克风选取的任意性，一个拥有n个麦克风的阵列对应的Num ＝个时延均满足上述性质。

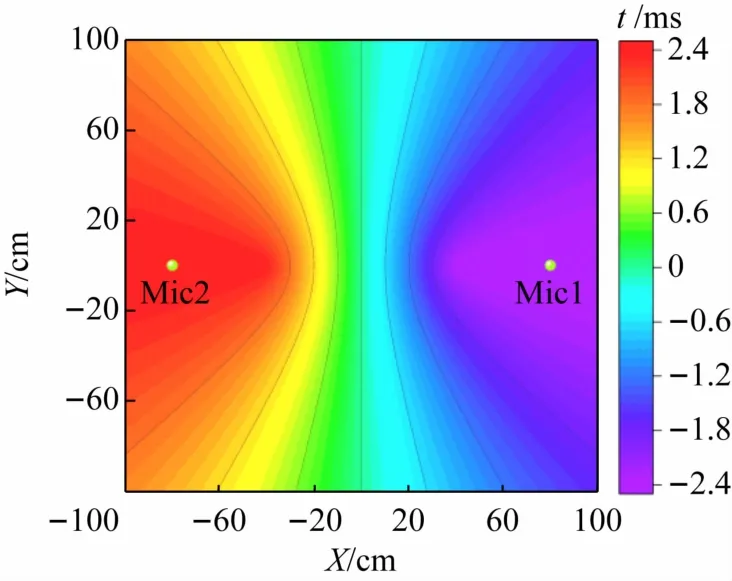
图2 时延分布图（d ＝80 cm）

（2）零时延值分布在垂直平分面上。当声源位于2 个麦克风的垂直平分面时，其对应的实际理想时延为0 s。如果考虑拥有n个麦克风的阵列，则其Num个时延估计结果中零时延的数量并非是0－Num之间连续取值的。以五元十字麦克风阵列为例，在单次估计的10 个时延中，为零值的数量只可能为0、1、2、4、6个（如图3 所示，其中6 个零时延对应的声源位置在中心麦克风处）。

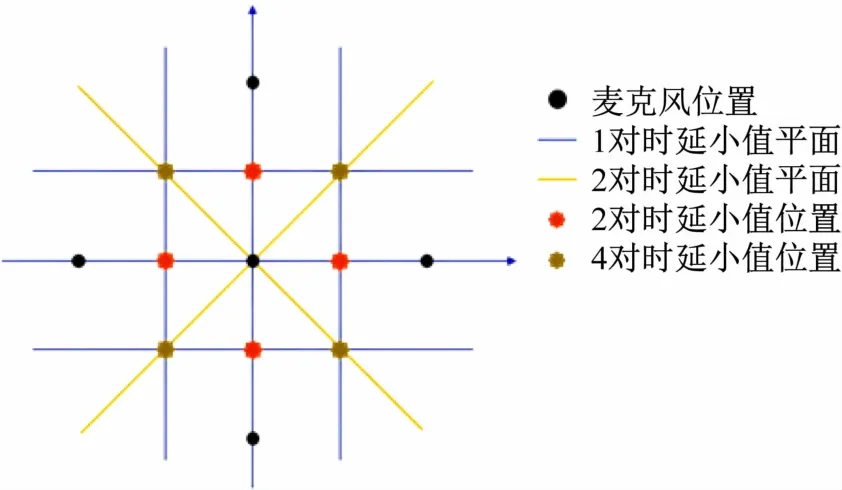
图3 五元十字麦克风阵列的小时延位置分布

在实际情况中，由于噪声等环境因素的影响和时间分辨率的限制，估计的时延值不可能刚好是0 s，而是接近于0 s的小值（时延估计值小于某一指标h，这里h取1 个时间分辨率）。这些小值的分布情况与零时延值的分布类似，对于单次估计的Num 个估计值，其为小值的数量只可取0、1、2、4、6。出现小值的声源位置相对来说定位更加困难，故称这些位置为定位盲区。需要对于较小的估计值单独进行考虑。如果小值总数不满足上述的规律，则该组时延估计结果一定不准确。

（3）时延之间具有线性相关性。对于任意3 个麦克风m、p、q，其到声源的距离Rm、Rp、Rq有如下关系：

两侧同时除以声速v可得

式中，τmp、τmq、τpq为指声源信号到达不同麦克风的理论时延值。

在实际情况中，时延的估计值总会存在误差。在误差允许范围的情况下，式（6）应该增加一个误差修正项：

式中：τ＾为时延估计值；Δ 为人为给定的时延估计的误差指标。

在实际测试中，为准确对声源进行定位往往需要用到多个麦克风，如果使用了n个麦克风，则有Num ＝个时延。这些时延并非完全独立，或者说它们是线性相关的（即满足式（7））。事实上，在传统方法中只是代入对应2 个麦克风接收到的音频进行估计，并没考虑同一次测量的不同时延之间内在联系，这会造成定位不准确。

综上所述，对于拥有n个麦克风的阵列而言，一次合理的时延估计应该同时满足：

（1）存在最大值τmax＝d／v。

（2）对于时延的估计值，小值的总数应该满足确定的分布。

（3）在误差允许的情况下，各时延之间应该满足式（7）的线性关系。

在实时的定位过程中，可在录制极短的音频后就开始时延估计，经过反馈机制的判断，再确认是输出合理的结果还是录制下一段音频（见图4）。

图4 引入反馈机制后的时延估计流程

为验证反馈机制的引入是有效的，在Matlab 仿真程序中进行预实验。预实验使用的是五元十字麦克风阵列，通过改变声源的位置来改变时延的真实值τ，估计值与真实值τ的偏小于1 倍分辨率（本实验为1／48 000 s）时，则认为估计值是准确的。在不同R0（声源到2 麦克风连线的中点的距离）处设置一系列信噪比（SNR），同一SNR 下进行104次实验，比较改进前（有反馈）、后（无反馈）时延估计值的准确率。其中改进前是指采集0.1 s音频直接代入定位算法；改进后是指采集0.4 s音频，然后将音频平均分为4 段，按照图4 的流程代入定位算法。

如图5 所示，在信噪比相同的情况下，随着距离R0的增加时延估计的准确率在下降。在R0相同的情况下，时延估计的准确率随着SNR 的增大而增大，并且改进后的准确率均要高于改进前。这说明引入反馈机制后能提升时延估计的准确率，时延估计算法的抗噪性得到了提高，改进是有效的。

图5 算法改进前、后时延估计准确率对比

2 定位算法

定位问题可总结为在最小误差的情况下，求得声源坐标。上述问题是非线性的，难以直接解决，可利用球形插值法（Spherical-Interpolation Method）将问题转化为线性最小二乘问题［12-13］。该最小二乘问题的解：

其投影矩阵：

式中，I为指单位矩阵。

利用时延估计算法得到的时延计算距离差的估计值δr＾后，代入式（11）可解得声源坐标估计值。

本实验使用五元十字麦克风阵列在二维平面上进行声源定位。麦克风M1～M4到中心麦克风M0的距离相等（见图6（a）），记麦克风阵列孔无特别申明后文实验中的d＝80 cm。以M0为原点建立如图6 所示的坐标系后，即可使用式（11）求解声源位置。

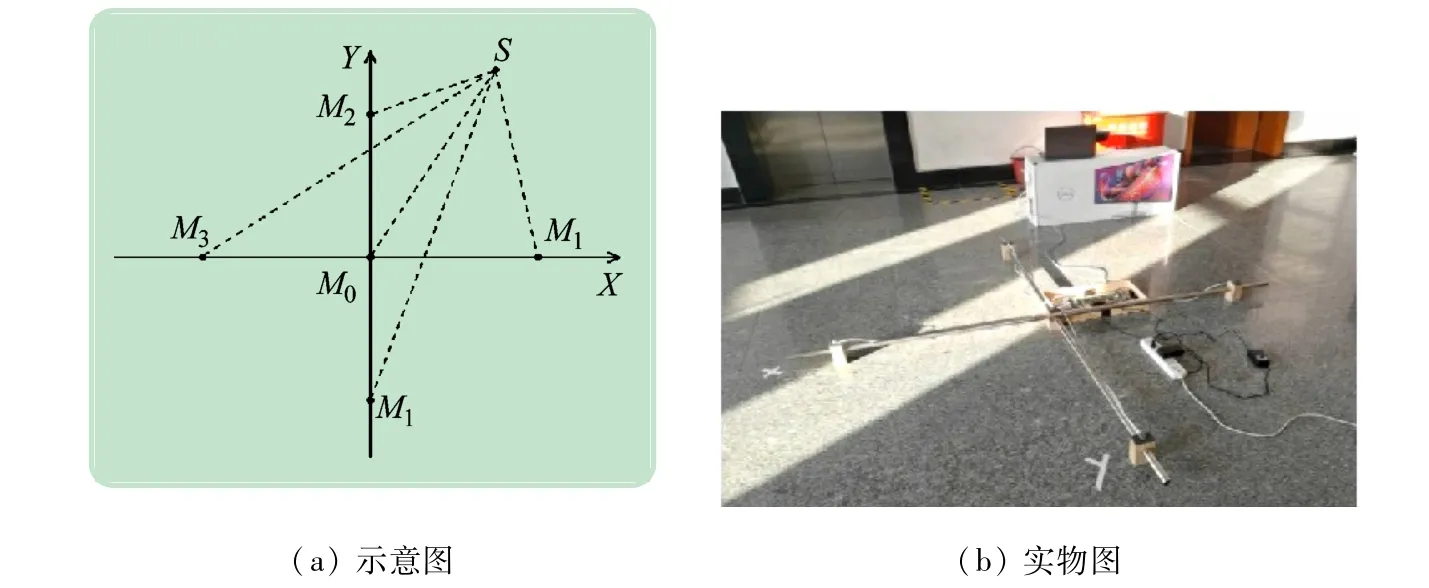
图6 五元十字麦克风阵列

3 实验结果

在Matlab 仿真程序中使用五元十字麦克风阵列进行定位实验，比较声源坐标的估计值X＾、Y＾和声源坐标的实际值X、Y，如果定位结果满足，则认为该次定位准确。本实验利用image方法［14-15］在5 m×5 m×5 m房间内产生声音信号，声源位于距离坐标原点不同R0的多个环形区域，在不同SNR和混响时间的情况下进行多次仿真，比较改进前、后定位准确率。在混响时间为0.25 s且SNR为－10 ～0 dB 的情况下进行多次实验。如图7（a）所示，在不同的距离R0处定位准确率均随着SNR 的增加而增加，且改进后定位准确率均要高于改进前。如图7（b）所示定位准确率的增幅在0 ～0.25 之间不等。在SNR为0 dB且混响时间为0.15 ～0.40 s的情况下进行多次仿真实验。如图8（a）所示，在不同的距离R0处定位准确率均随着信混响时间的增加而增加，且改进后定位准确率均要高于改进前。如图8（b）所示，定位准确率的增幅在0 ～0.20 之间不等。由此可见，改进后的算法的抗混响性得到了较好的提高。

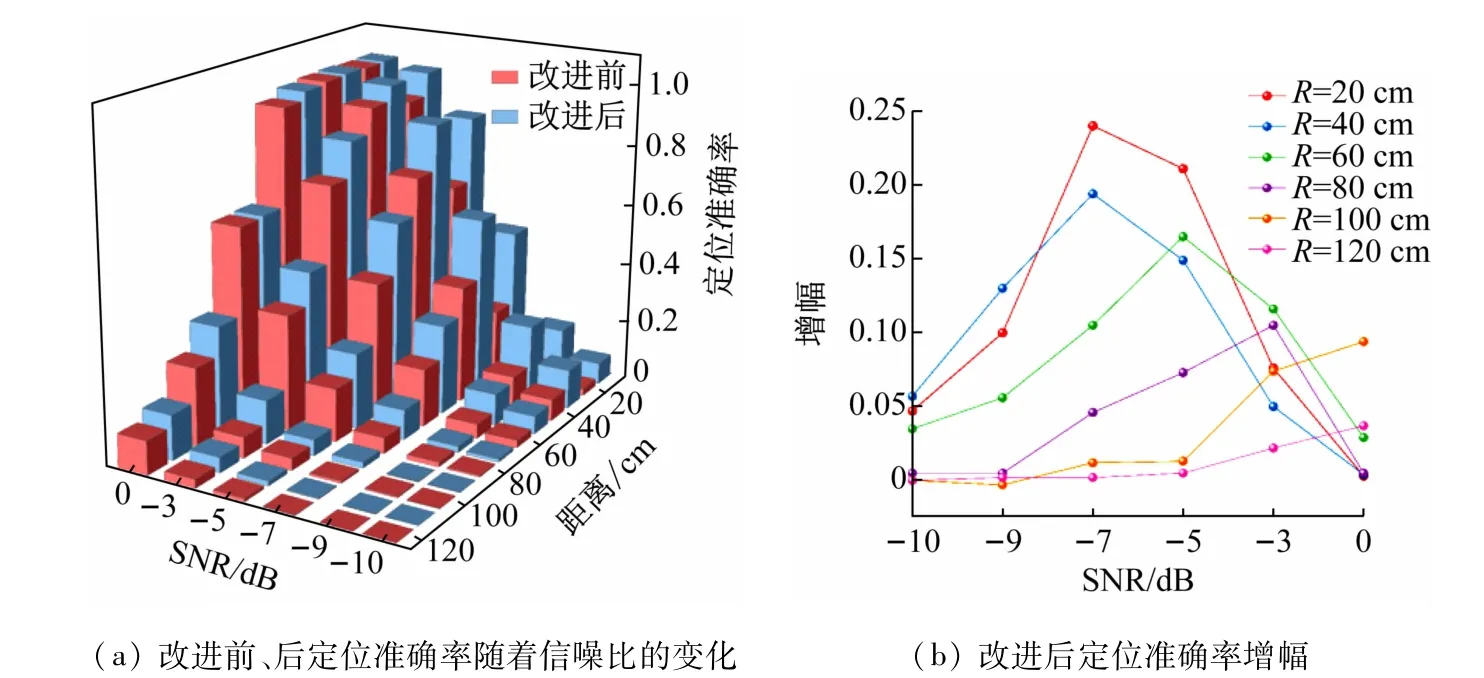
图7 不同信噪比下实验结果

图8 不同混响时间下的实验结果

在以坐标原点为圆心，半径为120 cm的圆形区域对定位准确率进行仿真（SNR ＝0 dB，混响时间t＝0.25 s）。同样的，如果定位结果满足，就认为本次定位是准确的。

如图9（a）、（b）所示，在某一个方向上，随着声源到原点的距离R0增大，准确率下降。当R0增大到1.5d＝120 cm时，已经难以得到较为准确的结果。而在距离R0一定情况下，靠近轴的部分定位准确率不佳（如图9（c）、（d）所示）。该结果有很强的中心对称性，这与麦克风阵列中心对称有关。相比较而言，改进后的定位结果要明显的优于改进前，并且原来盲区的定位准确度有着大幅度的提升。

图9 时延准确率分布图

图9 显示的定位准确度是关于原点中心对称，只需研究第1 象限中的定位结果。在第1 象限内控制声源到原点的连线与X轴的夹角φ ＝45°，改变声源到原点的距离R0进行定位仿真。同一个位置在SNR ＝0 dB、混响时间t＝0.25 s的情况下重复103次，计算出定位结果的均值和标准差（结果见表1、2）。为直观看到仿真定位结果，将定位结果表示为估计值-实际值图。如图10 所示，在R0＝0 ～80 cm 的范围内改进后的估计值要更加接近实际值，此外改进后标准差要明显小于改进前，并且随着R0的增大标准差的差异更明显。这说明在R0＝0 ～80 cm时，引入反馈机制后声源定位算法的精确性和稳定性均得到了提高。

表1 改进前仿真定位实验结果

表2 改进后仿真定位结果

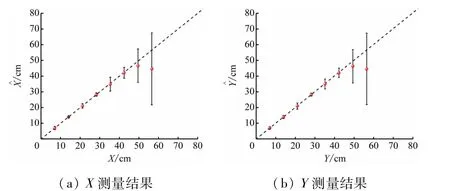
图10 改进前仿真定位实验结果

图11 改进后仿真定位实验结果

为验证定位仿真的结果，本实验搭建了一套五元十字麦克风阵列（见图6（b）），并在室内走廊进行了定位实验。定位结果见表3，坐标估计值保留到整数位，大多数估计值与实际值的偏差在1 cm以内，这一实验结果与仿真定位实验相符。这说明该设备能够实现厘米级精度的定位。

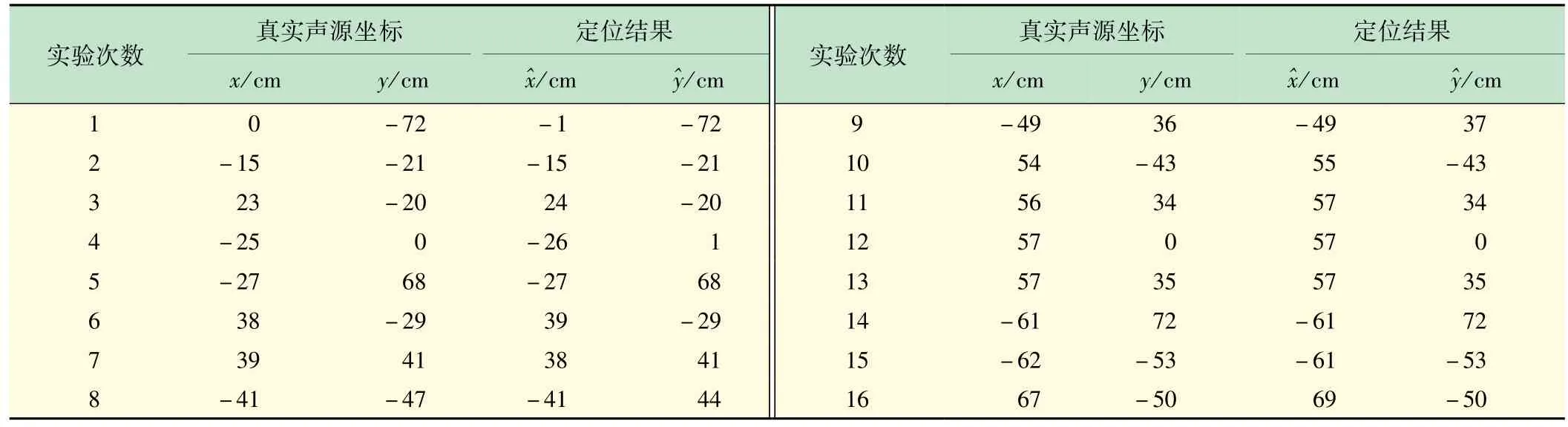
表3 定位结果（保留到整数位）

4 结 语

本文通过在时延估计算法中引入一种普适的反馈机制，提高了时延估计的准确率，实现更高精度的声源定位，在实验仿真的支持下最终搭建了一台cm 级的声源定位设备。实验仿真发现，引入反馈机制后该声源定位算法的抗噪性、抗混响性均有了不同程度的提升，定位的准确率的增幅最大可达20%，并且改进后对同一位置多次测量结果的标准差也要小于改进前，这说明引入反馈机制后，定位的稳定性更高。此外实验仿真表明，在SNR ＝0 dB、混响时间为0.25 s的情况下，对于孔径d＝80 cm 的五元十字麦克风阵列来说，其最大定位极限在120 cm 处。实际搭建的设备对虚拟仿真结果进行实际验证，发现可以实现cm 级的定位，与仿真定位实验的结果相符。该反馈机制只是根据麦克风阵列的几何形状引入的，不依赖于时延估计方法的选取。通过引入这一普适的反馈机制，使得声源定位算法的抗噪性、抗混响性和稳定性均有提高。该反馈机制对于噪声较大、混响较强环境下的声源定位具有一定的应用价值。