基于凝聚层次聚类算法的ATT&CK 模型改进∗

徐明迪 崔 峰

（武汉数字工程研究所 武汉 430205）

1 引言

随着网络空间中攻防博弈日趋激烈，攻击者渗透目标系统的路径变得更加复杂和隐蔽［1］，仅依靠人工进行分析和识别将难以应对。ATT&CK模型［2］作为网络攻防知识的一种“固化”，将其与网络安全工具结合，例如蜜罐系统、态势感知系统，能够提高网络安全威胁分析的自动化程度［3］，提高安全威胁捕获的效率。

ATT&CK 模型由MITRE 组织发布，在网络安全防御方面有诸多应用。国内外对与ATT&CK 模型也开展了许多研究，其中杨萍等［4］通过对大量恶意代码的详细分析，总结恶意代码各种行为事件实现的模式特征，基于ATT&CK 模型提出m-ATT&CK 模 型；潘 亚 峰 等［5］设 计 并 实 现 了 基 于ATT&CK的APT攻击语义规则模型，用于识别和标记攻击行为；文献［6］中对ATT&CK 模型中攻击技术之间的关联关系进行研究。

上述研究都是围绕ATT&CK模型展开，但没有对模型应用中的复杂性进行考虑。本文针对ATT&CK 模型的应用问题，提出一种基于凝聚层次的改进聚类算法，对ATT&CK 技术集进行聚类简化，提出一种将ATT&CK 技术集合量化的方法，并考虑到如何确定最佳聚类数据量的问题，将统计假设检验与聚类算法结合，由统计假设确定最佳聚类数量。

2 问题描述

应用ATT&CK 模型进行攻击行为识别和标记时，从战术层面和攻击手法层面都不适合直接应用。首先，ATT&CK 模型中战术的抽象层次较高，在ATT&CK的企业版中包括的战术有访问初始化、执行、常驻、提权、防御规避、访问凭证、发现、横向移动、收集、数据获取、命令和控制，可以看出上述的战术作为网络攻击阶段性的抽象描述，仅以战术阶段作为攻击行为的标签不利于对攻击行为的具体分析；其次ATT&CK 模型提供了一个包含440 项技术的集合，这个集合是作为不同类型攻击所涉及技术的超集，但MITRE 仅为模型中部分技术提供了检测规则描述，如果应用ATT&CK模型进行攻击行为识别将无法做到全部覆盖。因此本文在ATT&CK 模型的战术和技术层之间增加一层划分，解决战术层过于抽象和技术层无法全覆盖的问题。

在对ATT&CK 模型的技术集合应用聚类算法进行划分前，需要研究解决三个问题。首先，如何将ATT&CK 技术集合量化为特征向量；其次，聚类数量如何确定，如何为ATT&CK的技术集合找到最佳的聚类数量；最后，在聚类算法将样本聚类成k个簇后，如何确定得到的聚类结果具有意义。

3 方法概述

针对上述的问题，本文提出一种基于凝聚层次聚类算法的改进，用于对ATT&CK模型的技术集合进行聚类。算法改进部分是，在聚类流程中加入统计假设检验步骤，借助统计假设检验结果完成对聚类结果的有效性检验，同时确定最佳聚类数量。本节中对ATT&CK 模型技术集合的聚类研究按照图1所示的流程进行。

图1 模型改进流程

3.1 ATT&CK技术集量化

首先对聚类对象ATT&CK技术集合进行量化，为聚类算法提供数据基础。ATT&CK 模型中的技术均为文本数据，需要将其转化为向量数据集后才能应用于聚类算法，MITRE 对于技术按照表1 中提供相关字段的组织技术的文本介绍（表中仅列出部分字段），虽然技术的介绍在整体上看是具有结构的，但在不同字段内文本内容是非结构，受作者的写作风格等因素影响。

表1 ATT&CK模型中技术介绍

参考表1，可以看出与技术相关的数据大部分由文本组成。因此在考虑量化方法时，首先考虑直接对于文本数据的量化，采用自然语言处理领域中常用的处理步骤，对文本数据进行分词、量化等处理［7］，采用上述方法进行量化存在两方面的不足，首先不同技术描述文本受其作者的主观因素影响较大；其次直接进行分词量化，因不同文本长度不同得到的特征向量维度也不同，如果在实现过程中对不同向量维度进行截断或填充，可能会丢失部分信息。考虑到上述不足，直接采用自然语言处理领域中的文本量化方式是不合适的。通过查阅文献，在本文中使用同样由MITRE 提供Groups 知识库，完成对技术数据集的量化。

Groups 是一个用于整理网上公开入侵情报的知识库，其作用和贡献主要是，在安全社区中确定一个通用、统一的名称进行入侵活动的跟踪，分析人员使用各种分析方法和术语跟踪活动集群，例如威胁组、威胁参与者、入侵集和活动。

在量化过程中，本文主要使用表2中的技术/子技术字段，在Groups 知识库中，每个APT 记录视被为攻击实例，并将每种技术均作为攻击实例的组成属性，其形式化表达如式（1）所示，式中tn代表ATT&CK模型中的技术，T代表技术集合。

表2 Groups中攻击实例描述

本文采用特征工程中的二值编码方法。二值编码是常用且易操作的量化方式，它只依据某个特征决定是否存在，来决定特征向量中对应位置是1或0，而不是量化出现次数。借助Groups 知识库，将ATT&CK 模型中的技术统一映射为81 维向量，映射策略为向量中每个维度代表一个Groups 中的攻击实例，如果该技术在攻击实例中被使用，则该维度的值为1，反之则为0。经过上述的映射方法处理后，数据集由离散的高维向量组成，特征的结果为0 或1，分别表示攻击实例中某个技术的负面或正面发生。

在利用Groups知识库量化的过程中，为了避免并产生误导性的技术关联，本文中使用至少包含五种不同技术的攻击实例进行量化，在本节接下来的部分中对于ATT&CK 技术集合量化得到的向量数据集，均简称为ATT&CK数据集。

3.2 聚类趋势评估

对ATT&CK数据集进行聚类趋势评估，判断其是否具备聚类的基础，保证聚类结果的合理性。聚类趋势评估用于检验样本分布的空间随机性，从而判断数据是否可以聚类，进行聚类趋势评估的必要性是因为即使在数据集中没有显著的组时，聚类方法也经常可以返回聚类结果，无论类别下的样本是否相关［8］。

在聚类趋势评估中使用霍普金斯统计（Hopkins statistic）［9］方法，Hopkins 统计由Brian Hopkins和John Gordon Skellam 提出，是一种空间统计量，检验空间分布的变量的空间随机性，可以看作是对于给定的数据集D，它由随机分布生成的概率。具体操作是将数据集D中的点之间的距离与从随机模拟的数据集DR中得出的点之间的距离进行比较。具体计算步骤如下所示，

1）随机从D中抽取n个点p1,p2,…,pn，对每个点pi(1 ≤i≤n)，找出pi在D中的最近邻样本点，并令xi为pi与它在D中的最近邻之间的距离。

2）随机从DR中抽取n个点q1,q2,…,qn，对每个点qi(1 ≤i≤n)，找出qi在DR中的最近邻样本点，并令yi为qi与它在DR中的最近邻之间的距离。

3）根据步骤1）、2）得到的结果，计算霍普金斯统计量。

在上述步骤中，D表示对ATT&CK 模型技术集合量化后得到的数据集，dist()为计算样本间距离的函数，函数中分别使用Jaccard 距离［10］和Phi系数［11］进行计算得到不同距离，关于距离度量的选取说明在3.3 节中进一步进行分析。在步骤1）、2）中，随机数据集使用伯努利分布生成，结合数据集的性质能保证是在样本空间中均匀取点。对于式（4）的计算结果H，假设D是均匀分布的，缺乏聚类趋势那么，H将约等于0.5。因此，如果H为0.5可以得出数据是均匀分布的、没有任何有意义的聚类；假设D不是随机分布且具有聚类趋势，那么H将约等于1；对于H约等于0 的情况，此时D可以被认为既不是随机也没有聚类趋势。

对ATT&CK 数据集使用Jaccard 距离和Phi 系数计算霍普金斯统计量，Jaccard 距离得到的HJ为0.59 和Phi 系数得到的HΦ为0.63。HΦ值高于HJ表明使用Phi 系数可以使ATT&CK 数据集具有更好的聚类趋势。

3.3 基于凝聚层次聚类的改进算法

凝聚分层聚类算法适用于查找具有最大相似性的集合，因为本质上该算法是贪心策略的一种实现，在聚类决策过程中，每一次聚类都是将目前最相似的两个簇合并，直至聚类结束，从而保证得到聚类结果是最相似的。凝聚层次聚类算法首先得到样本数据的多级分层，然后通过指定聚类数量k或截断高度得到最终聚类结果。

在获得ATT&CK数据集之后，可以使用层次聚类算法获得最终树状图，但仍然不能推断出技术之间关联，因为需要确定树的截断高度（即最后的聚类数量）。因此本文提出一种基于凝聚层次聚类算法的改进，在聚类流程中加入统计假设检验步骤，借助统计假设检验结果进行聚类数量的选择。

在统计假设检验步骤中采用的零假设验证，通常是数据分析实验的一部分，指进行统计检验时预先建立假设，零假设成立时有关统计量应服从已知的某种概率分布，当统计量的计算值落入否定域时，可知发生了小概率事件，应否定原假设［12］。

将统计假设检验与聚类算法进行结合，将ATT&CK 数据集产生的树状结构与零分布产生的树进行比较来分析聚类的有效性，并允许在所需的置信度水平上推断出统计上显著的结果，统计假设检验所用的数据集由随机伯努利分布生成，产生的数据与ATT&CK数据集具有相同方差，随机数据集上产生的空树表示为T0。如果在指定的阶段高度TD中的簇数与T0的簇数明显不同，则聚类产生的结果将具有统计意义。具有统计意义的层次结构树的结果可以得出这样的结论，即所产生的关联不同于随机产生的结果，从而为技术关联提供了有效性基础。基于凝聚层次聚类的改进算法流程如下。

应用聚类分析ATT&CK 数据集的过程是根据每个数据之间的相异度进行划分，因此选择相异度的度量标准对于聚类结果有较大影响。在应用中，聚类算法多使用特征空间中的欧式距离作为度量标准计算不同样本之间的相异度［13］。当使用欧式距离作为相异度测量时，样本之间的距离越小，则说明两者之间越相似，越有可能被划分到同一个簇。聚类使用的相似性度量（或称为距离度量）是在样本数据上执行，因此相似性度量方法随样本集性质的不同而不同。因此必须对本文中使用的数据集中的变量使用合适的距离度量。欧式距离度量标准通常应用于连续变量，而本文中的ATT&CK数据集具有离散性，因此需要考虑欧式距离以外的度量方法。

对于ATT&CK数据集的数据由二元变量组成，通过查阅文献［6］确定Jaccard距离和Phi系数相关距离是最合适的。Jaccard 距离是用来衡量两个集合差异性的一种指标，Jaccard 距离是Jaccard 相似系数的补集，被定义为1减去Jaccard相似系数，Jaccard 相似系数是用来衡量两个集合相似度的一种指标。在用于本文中计算任何两个技术Ti和Tj之间的Jaccard相似系数时，定义如式（5）所示。

其中，需要n的下标为两个数字，从左至右分别代表Ti和Tj是否出现，n11代表Ti和Tj出现在同一个APT 攻击实例中的频次，n01代表Ti不出现在某个APT 攻击实例而Tj出现的频次，n10与n01定义相反，在式（5）中Jaccard相似系数的计算不考虑n00的值。Jaccard距离度量技术Ti和Tj之间的不相似度，并定义为Jaccard 相似系统的补码，即1-Js(Ti,Tj)。Jaccard 距离可以解释为，Ti和Tj涉及的攻击实例的交集除以它们的并集之比。

Phi 系数是一个经验的非参数相关度量，专门用于二进制数据。在使用Phi 系数度量不同技术时，首先将待度量的技术排成2×2 表，具体排列情况见表4。Phi系数的基本概念是，两个二元变量的观察值若大多落在2×2 列联表的主对角线字段，则这两个技术呈正相关。反之，若两个二元变量的观察值大多落在非对角线字段，则这两个变量呈负相关。任意两种技术之间Phi 系数与计算方如式（6）所示。

式（5）、式（6）中出现n的定义见表3。

表3 Jaccard距离和Phi系数中n值定义

在确定样本间的距离度量方式基础上，在本文中使用Ward链接［14］作为簇间距计算方式。因为相比于Ward链接，单链接方法会创建松散的簇；全链接方法会创建紧密的簇，但异常点对聚类结果影响较大。

4 实验结果分析

在本节实验部分通过数据预处理、选取评价指标、算法实现和设计对比验证凝聚分层的改进聚类算法的效果。

4.1 聚类结果对比

在实验对比中，本文对ATT&CK数据集采用模糊聚类算法［15］中的PAM 算法进行［16］聚类，将模糊聚类得到结果与凝聚层次聚类算法得到的结果进行比较。

图2 每种划分的聚类方法的聚类图和相应的数据集用不同的颜色表示，其中横纵坐标轴为ATT&CK 数据集的维度1 和维度2，图像中的轮廓为数据集在维度1和维度2组成平面上的投影。模糊聚类算法对ATT&CK 数据集的结果如图2 所示，从指定维度上的投影可以看出，得到的技术聚类之间相互重叠和包含，难以区分任何潜在的技术关联。

图2 模糊聚类结果

对于ATRT&CK 数据集，学习到的层次聚类树的结果如图3 所示，通过基于凝聚层次的改进聚类算法最终得到54 个簇，每个簇在树中以不同的颜色表示。由于层次聚类算法的特点，聚类结果不会出现簇间的交集，因此需要对改进聚类算法的结果进一步分析，验证得到聚类结果是有效的。

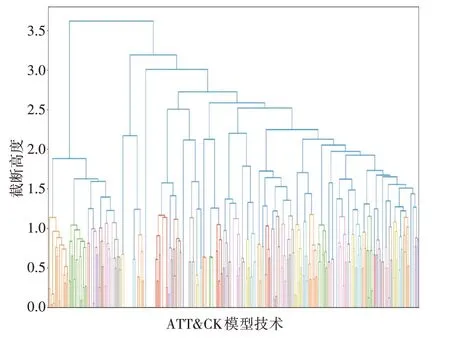
图3 基于凝聚层次改进的聚类算法结果

4.2 结果分析

通过选取部分聚类结果进行原理分析说明聚类结果的合理性，对聚类得到的子集合{T1494，T1115，T1485，T1486，T1487}进行分析，集合中的元素按照顺序分别代表端口监控、运行数据操纵、发送数据操纵、剪贴板数据获取、数据破坏、破坏性数据加密、磁盘数据结构擦除。由包含的攻击技术可以看出，该子集代表了一种窃取或破坏数据的攻击模式。该模式下，攻击者可以通过运行数据操纵、发送数据操纵来间接影响目标进程的正常运行，或者进行数据收集、窃取信息，然后在下一步中可以选择数据破坏也可以进行加密勒索。上述的顺序关系只是举例说明，实际环境下可能是窃取、加密勒索等同时出现。

攻击技术的子集对于ATT&CK 模型的改进主要体现在两方面，首先，提高蜜罐监控的针对性，可针对ATT&CK模型的技术子集进行数据监控；其次提高关联分析的能力，当捕获到子集中一个攻击技术时，应该关联考虑子集中其他攻击技术，这些攻击技术出现的可能性较高。

针对网络攻击模型应用于蜜罐系统，分析应用过程存在的问题，并提出一种基于凝聚层次聚类的改进算法，用于对ATT&CK模型的技术集合进行聚类。改进算法在聚类流程中加入统计假设检验步骤，借助统计假设检验结果对聚类结果的有效性检验，同时确定最佳聚类数量k。对比不同聚类算法分析和分析聚类结果，验证改进聚类算法能够对ATT&CK模型的技术集合产生有效聚类结果。

5 结语

本文针对ATT&CK模型的应用的复杂性问题，提出了一种基于聚类算法的ATT&CK 模型改进方法，首先使用Groups 知识库对ATT&CK 技术集合进行量化，在量化得到的特征向量数据集上使用Jaccard 距离和Phi 系数相关距离进行聚类趋势度量，验证量化后的数据集具有聚类趋势，最后在凝聚层次聚类算法中加入统计假设验证用于确定最佳聚类数量，并通过实验和分析验证聚类结果的有效性。