基于A*和动态窗口法的移动机器人路径规划∗

王佳军 孟令军 薛志凌 李晓宇

（中北大学仪器与电子学院 太原 030000）

1 引言

随着科技水平的快速提高，机器人由最初的结构简单、功能单一发展为能够适应多样化环境、执行复杂任务的智能化机器人，广泛应用于物流业、制造业、服务业等领域，极大地提高了社会的生产力水平。而路径规划是实现自主导航的关键一步，也是机器人智能化的关键技术之一，是机器人以及自动驾驶领域的研究热点。目前，机器人路径规划主要集中在三类算法：1）基于图的算法，如：Dijkstra、A*算法［1］，D*算法［2］，D*Lite算法［3］等；2）随机采样类算法，如：快速随即搜索树法（RRT）［4］、概率路图法（PRM）等；3）智能优化算法：如蚁群算法、遗传算法、神经网络等，此外，还有人工势场法［5］，动态窗口法［6］等。

Dijkstra 算法基于广度优先遍历，向四周盲目拓展，搜索节点过多。A*算法在Dijkstra 算法的基础上引入启发式函数，增强了搜索的目的性，在机器人全局路径规划中使用广泛。但是该算法存在节点过于密集、轨迹不平滑等问题。文献［7］利用跳点搜索理论，大大减小了搜索过程中节点的数量；文献［8］引入电动车的能耗约束建立综合估价函数，同时考虑中途充电站，规划出能耗最优的行车路径；文献［9］将传统A*算法八角度拓展节点优化为任意角度路线，减小了路径长度，与蚁群算法进行融合实现多目标点路径规划。

动 态 窗 口 法（Dynamic Window Approach，DWA）对复杂环境具有很强的适应能力，实时结合机器人自身传感器进行局部路径规划，能够有效躲避障碍物且路径为平滑曲线，但是该方法容易陷入局部最优解，无法抵达目标点。文献［10］结合与全局路径距离信息定义新的评价函数，能够提前规避“C”型障碍物；文献［11］结合自适应思想使得机器人在通过不同密度障碍物区域时，运动参数能够自主变化，机器人的速度与路径更加合理；文献［12］利用动态窗口法对可选避障速度进行速度约束，同时，增大了移动机器人可选避障速度区域。

本文将A*算法与动态窗口法结合，首先对A*算法产生的路径节点进行预处理，剔除冗余节点，得到路径坐标点作为动态窗口算法的局部目标点，直至最终目标点，有效解决了单一算法在路径规划中存在的问题。

2 A*算法

2.1 环境构建

在机器人工作过程中，需要通过自身传感器感知环境，构建一个机器人可以理解地表示所在环境的地图模型。栅格法是经典的环境建模方法，简单高效，将机器人构建的地图划分为大小相同、彼此相连的栅格，栅格带有环境信息及机器人位置信息，机器人以栅格为基本单元进行移动和搜索，完成路径规划任务。如图1所示，深色栅格表示环境中存在障碍物，机器人无法通过，浅色栅格表示允许搜索区域。

图1 栅格地图

2.2 A*算法基本原理

A*算法在搜索过程中假设环境不再改变，是求解最短路径的有效方法。Dijkstra 盲目向四周搜索，而A*算法的改进在于结合当前位置与目标点的距离建立具有启发性的搜索函数：

式中：g(n)为起始节点至当前节点的实际距离代价；ℎ(n)为当前节点至目标点的估计距离代价。

代价函数f(n)来进行节点的扩展和搜索，g(n)代表搜索的完整性，g(n)越大越趋向于搜索的广度，但会降低搜索的效率，h（n）具有启发性，h（n）越大，搜索的效率高，但通常难以规划到最优路径。

A*算法沿着栅格地图搜索的过程中，更新维护open list和close list两个列表。Open存储拓展点周围节点，用于计算选择最小代价节点作为下一个拓展点，close 存储经过的节点以及障碍物。A*算法具体流程如下：

1）初始化环境信息，包括障碍物、起始点、目标点，以及open和close列表；

2）判断open 列表是否为空或只有目标点，若为真，结束搜索；

3）选取open 列表中评价函数最小的节点作为父节点，调用拓展函数，计算g（n），h（n），将此节点放入close列表；

4）将拓展出来的节点放入open 列表中，保存父节点；

5）跳至步骤2），直至找到终点；

6）保存的父节点信息，即为路径关键节点。

3 动态窗口法

动态窗口法由机器人运动学方程推导而来，在预测时间dt内，对机器人线速度和角速度采样，形成速度空间(v,ω)，描绘出所有可能的运动轨迹，构建评价函数对轨迹进行评价，从中选择最合理的路径。

首先，我们建立机器人的运动模型，机器人的运动轨迹由一系列的圆弧组成，在dt时间内由速度对(v,ω)决定，运动模型为

依据上述机器人运动模型，在机器人的实际工作中，具有无穷多(v,ω)，需要根据环境和工作状态添加约束，选择出朝向目标、躲避障碍物的(v,ω)。

出于安全考虑，对机器人行驶的速度范围进行约束，定义Vs为机器人最大线速度和角速度，所以动态窗口所能搜索的最大范围为

由于机器人电机所提供转矩的限制，机器人在dt时间内所能达到的实际速度受到一定的约束，即：

为了保证机器人在行驶过程中避免与障碍物发生碰撞，当机器人检测到环境中障碍物时，能够以最大减速度停下来，即：

最终，由以上三个速度构成动态窗口速度集合Vr：

经过速度采样后得到速度空间，如何在该空间内选择一条最优的轨迹，需要我们设计适宜的评价函数，使得机器人朝向目标快速前进，局部避开障碍物。评价函数设计为

式中：σ为平滑系数，α,β,γ为各子函数加权系数；heading（v，ω）表示当前位置与全局之间的角度偏差，使机器人朝向目标点方向；dist（v，ω）表示生成的速度轨迹至障碍物的最近距离，防止机器人发生碰撞；vel（v，ω）表示采样轨迹中的速度大小，尽快抵达。

4 优化与改进

A*算法根据评价函数，遍历整个栅格地图，得到一系列路径点，导致路径点过于密集，曲率不连续，关键拐点选取策略，剔除不相关的冗余节点，提升路径的平滑度。设A→B→C 为路径中三个节点的行驶路线，若A 与B 共线，B 与C 共线，则认为B节点为冗余节点，删去该结点。

传统评价函数从方向性、安全性、效率性方面充分评价速度空间内最合理的速度。向方向子函数加入全局路径信息约束：全局路径距离当前位置最近的节点之间的角度，新的方向函数保证机器人不断跟随新的目标点前进。该改进方法有效地解决了动态窗口法中单一目标点容易陷入局部最优的缺陷，规划出的路径即为全局最佳路径，改进后算法具体执行步骤如下：

1）根据机器人传感器构建栅格地图；

2）初始化A*及DWA参数；

3）A*算法进行搜索，获取关键全局路径点信息；

4）根据机器人运动模型，计算当前动态窗口Vr；

5）根据机器人运动模型，计算预测时间dt内运动轨迹点，同时根据评价函数对各轨迹点打分，分数最高者为下一个dt时间机器人的运动速度；

6）判断机器人是否到达目标点，若抵达，寻路成功，否则，返回第4）步，继续搜索。

5 仿真与分析

为了验证本文算法的有效性，在Win10 系统Matlab R2016a 环境下构建栅格地图进行仿真实验。根据文献［13］，机器人运动参数设置为Vmax=1.0m/s，ωmax=20°/s，V.max=0.2m/s2，ω̇max=50°/s，速度分辨率和角速度分辨率分别为0.01m/s，1°/s。各评价子函数系数分别为0.05，0.4，0.1。起始点、目标点分别为（1.5，2.5），（10.5，9.5）。

传统A*算法规划路径如图2所示，当搜索邻域由4邻域变为8邻域时，路径节点数、路径长度和转弯角度有了明显改善。实验数据如表1所示。可见，随着搜索邻域的增加，比如：24 邻域［14］，48 邻域［15］，运行时间没有明显增加，转弯角度降低，路径更加平滑。同时，坐标（3，3），（6，5），（8，9）处距离障碍物距离过近，导致路径的安全性降低。

表1 仿真实验数据

图2 全局最优路径及节点

图3 全局最优路径及关键节点

由图4 可以看出，传统DWA 算法规划路径时会陷入局部最优，寻路失败；由图5可知，与A*算法融合改进后得到新的路径为平滑曲线，距离障碍物距离更加合理，提高机器人行驶的安全性。本文得到运动学参数结果图6所示，速度和角速度连续变化，整体符合要求。在迭代次数为300 次通过稠密障碍物时，机器人方向出现小幅度震荡，在今后的研究中还需要改进。

图4 DWA路径

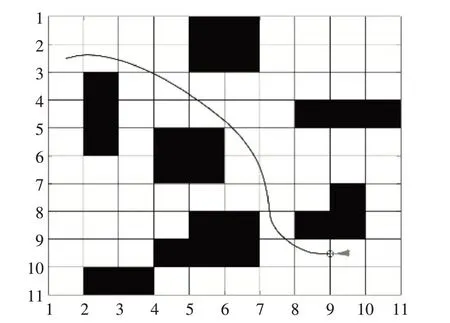
图5 改进型DWA路径

图6 速度曲线

6 结语

为了提高机器人在复杂动态环境下的表现，结合A*算法全局路径最优的特点和动态窗口法局部最优特点，提出一种新的算法。仿真结果表明，相较于单一算法，混合算法克服了局部最优问题，平滑度上有了巨大改进。但是在经过稠密障碍物时，还需进一步改进。本文仅仅做了初步的研究和实验，在今后还将在多目标、实时性方面做更多的探索。