基于改进遗传算法和Apriori 算法的气旋强度预测方法∗

刘 健 江天乐

（1.南方海洋科学与工程广东省实验室（珠海） 珠海 519080）

（2.复旦大学 上海 200433）

1 引言

在气象学中，气旋是指围绕着低气压的中心旋转的大型气团，通常所说的台风或者飓风都属于气旋。以我国为例，平均每年有约7 个气旋登录，带来严重的财产损失［1］。气旋预报对于灾害预报十分重要，气旋路径的预报准确率已经有了大幅度提高，但气旋强度预测准确性并不如对气旋轨迹预测的准确度高［2］。导致轨迹与强度预测之间的这种差异的主要原因是影响气旋强度变化的因素有很多，目前科学家还没有完全掌握气旋强度变化的机理，这使得能够预测未来气旋强度变化较为困难［3～4］。

迄今为止，所使用的最稳定的气旋强度预测模型是基于数值模拟或回归模型［5］，计算过程较为复杂，初始状态干扰相对较大，需要设计大量特征［6］。Jarvinen 等［7］早在1979 年建立了SHIFOR 强度预测模型，可以预测72h 内的强度变化。后来，Pike［8］、Merrill［9］等在此模型基础上，将气候影响因子导入模型，预测效果有所进步。DeMaria 等［10］在1994 年利用多元线性回归方法建立了SHIPS模型，导入如海表温度等更多影响因子，预测效果有了较大提高。Drton M 等［11］提出的基于马尔科夫链来实现气旋强度预测，其准确度由聚类的准确度决定，用于气旋预测的实用性不足，如果将输出结果仅作为未来6 小时候的气旋强度预测结果，该模型的预测准确度将会非常低。

通常将神经网络模型认为是一种黑盒模型，即它可以直接输出所解决问题的结果，Baik J J 等［12］利用神经网络对气旋强度进行了预测且获得较好的预测结果，但是对于结果无法做出合理解释。黄小刚等［13］应用神经网络模型建立了西北太平洋热带气旋强度预测模型，预报结果评测优于线性回归方法结果，但预报稳定性随着时效的增长在减小。

已有的关联分析预测模型也存在一定的缺陷，例如，挖掘关联规则的过程中很容易忽视一些极端的现象，这些现象出现频率较低，尤其是气象环境监测领域，极端气象现象总是对周围环境造成较大的影响［14］，而Yang R 等［15］提出的基于关联分析对气旋强度进行预测时，对所有预测因子的最小支持度阈值均为同一个值；另外，已有的气旋强度关联分析预测算法中，没有考虑到所有预测变量的变化情况，最终所获得的规则只能反映出，当某些预测变量的实际值处于某个范围时，可能会导致气旋强度发生变化。虽然关联分析可以发现现象的变化规律，但是由于先天缺陷，并不适用于预测领域，使用规则预测无法达到较高的准确度，利用关联分析对气旋强度进行预测仍有很大的改进空间。

2 数据处理

2.1 数据来源

本文中的研究数据来自SHIPS 目前已公布的全球气旋监测数据，数据按分布区域划分：大西洋（1982-2016）、东北太平洋（1982-2016）、太平洋中部（1982-2016）、西北太平洋（2000-2012）、北印度洋（1998-2012），1982 年-2016 年间出现的1902 个气旋，共计45385条记录。

如表1 所示，列举了气旋监测的部分参数，其中VMAX 用于衡量气旋强度。目前，SHIPS 提供的气旋监测数据中，同一个气旋每条气旋监测记录的时间间隔为6 个小时，每条记录都记录了那一时刻的气旋各个预测因子的实际值。

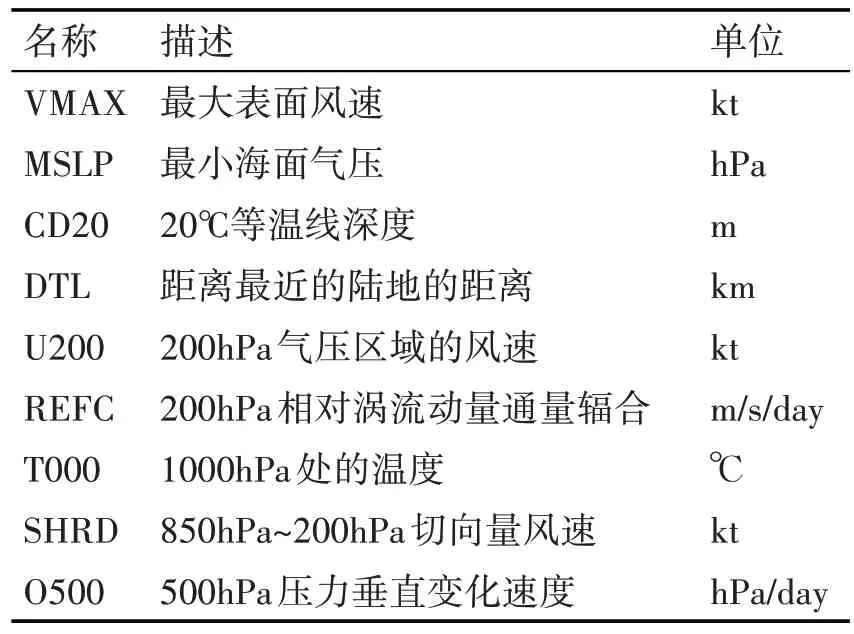
表1 气旋监测的主要参数

2.2 数据预处理

原始的气旋记录，不能直观地反映气旋的强度的变化，以及气旋的每个参数的变化趋势。气旋是一个极其复杂的系统，监测要素之间的相互影响共同决定气旋强度未来的变化，而要素之间的相互影响不仅仅是要素值的高低造成的，要素值的变化趋势也是不可忽视的。本文主要目的是实现预测气旋的强度变化，即VMAX在未来会有怎样的变化趋势，为了预测变化趋势，必定需要携带有变化信息的输入变量来进行预测，这类信息只有通过对比两条相邻的记录才能获得，由此引入了滑动窗口。

为了描述气旋的当前状态，引入了一个时间跨度为12 小时滑动窗口，由于气旋每条记录之间的时间为6 小时，即一个窗口内仅包含了三条记录，如图1 所示，通过滑动窗口将三个时刻的数据整合成了一条数据，这条数据由三部分组成，以图中的窗口为例，滑动窗口W1内包含了T1、T2 和T3 时刻的气旋数据，首先计算时刻T2 和T1 相同预测要素监测值的差，将差值根据所制定的范围进行离散化，输出该要素在T1 到T2 时刻之间发生变化，然后再根据T2 时刻要素值所处的范围进行离散化，可表示当前时刻（T2 时刻）各要素值所处的等级，最后计算T3 时刻和T2 时刻气旋强度的差值，得到气旋强度的变化值，根据制定的范围，得到气旋强度的变化情况，即未来的时刻（T3 时刻）气旋强度发生的变化。处理后的数据相较于处理前包含了更多信息，即要素的变化趋势信息，用这样的数据预测未来气旋强度变化也更加合理，有助于提高气旋强度预测模型的预测准确度。

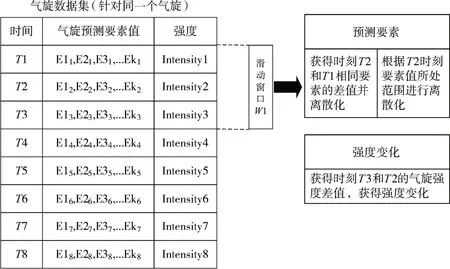
图1 滑动窗口处理数据

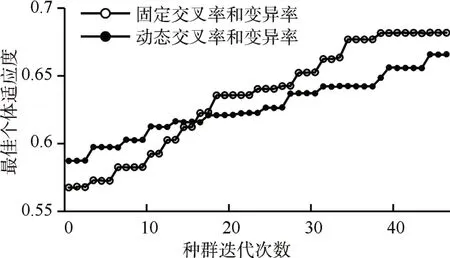
图2 最佳个体适应度对比

因为气旋的状态是一个不断变化的过程，当某一个要素数值处于某个范围内时会对其造成一定的影响，而且当某个要素的值在短期内发生了急剧的变化，或者在短期内没有发生剧烈变化，这也会对未来的气旋强度产生一定影响，目前已有的气旋强度预测模型均没有考虑要素的变化，这使得最终的预测结果准确率不理想。最终，每个要素均会得到两个量来进行描述，分别表示数值变化程度和数值当前所处范围。

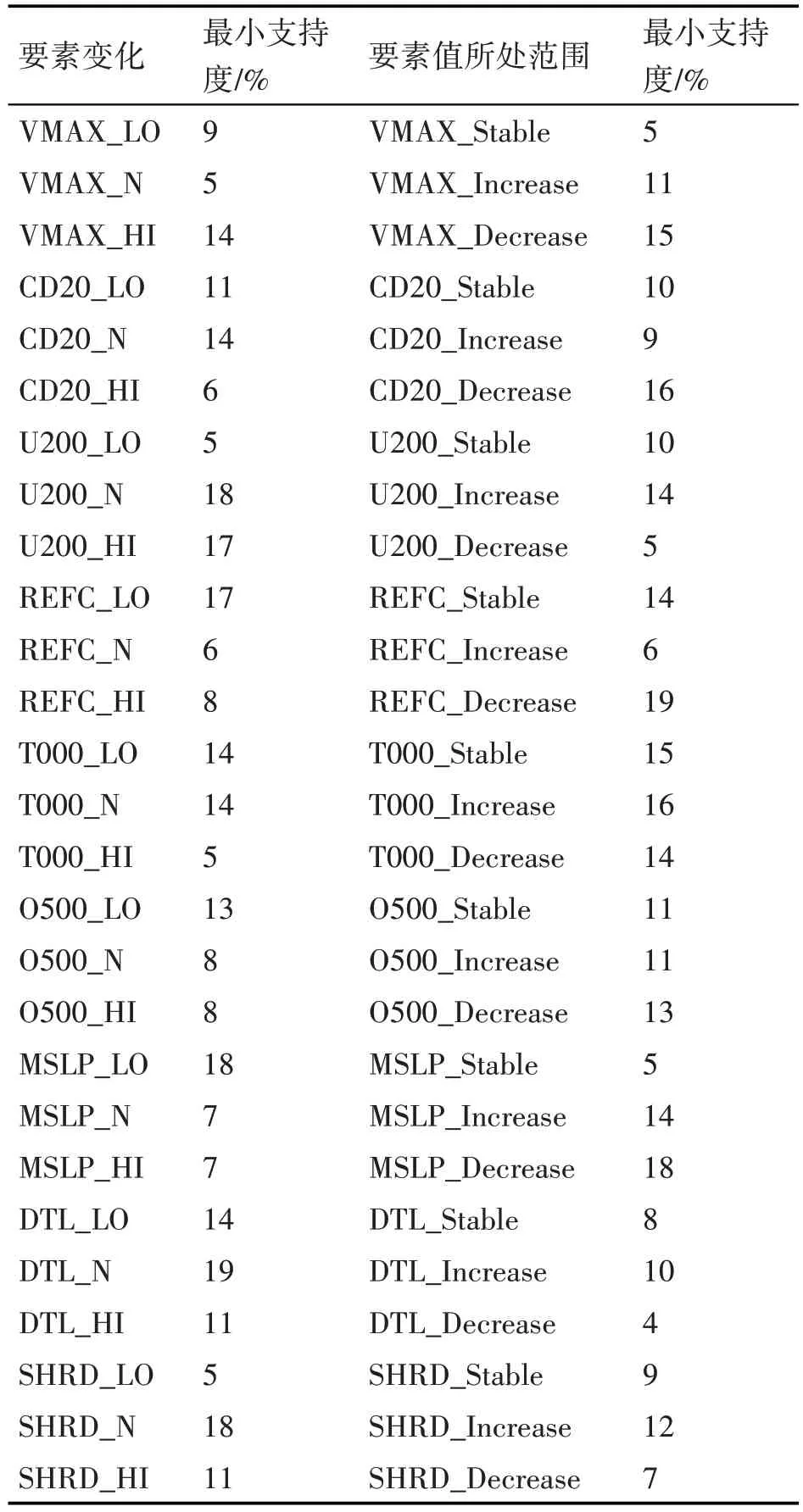
基于上述思想将其转化为用于Apriori 算法发现规则的事务型数据。分别将各个气旋强度预测变量的值划分为三个范围，分别用低（LO）、中（M）、高（HI）来表示，从而实现离散化，假设某个要素的值为X，m表示该因子的平均值，s表示其标准差，当X ≥m+s/2 时，用HI 来表示，当m-s/2 ≤X

3 GA-MSApriori预测算法

GA-MSApriori 算法将遗传算法和Apriori 算法相结合，遗传算法通常用于找到给定问题的最佳适应性的个体，作为该问题的解决方案，借助群体中的个体经历进化过程，通过模拟物种在自然选择过程中的物种选择和遗传机制，通过多次迭代过程筛选候选物种，并对保留下来的物种进行组合，从而产生下一代的候选物种，重复迭代直到满足某一个收敛条件，以此来解决最优化问题。本文中需要解决的是如何确定各个要素的最小支持度，以获得预测准确度最高的规则。

所有项的最小支持度均被转换为二进制，连接成一串二进制序列，作为遗传算法中的染色体，如果选取了m个要素作为模型预测的输入，经过滑动窗口处理之后会产生6m 个项，如果每个项的最小支持度用n 位二进制数表示，则每条染色体的二进制串长度为6mn，求最优解的搜索空间大小为2^6mn，本模型中每个项的最小值支持度限制在5%～20%之间，所以采用4 位二进制来对支持度进行编码，选取的参数有9 个，所以整个搜索空间的大小为2^216。GA-MSApriori中通过选择、交叉、突变实现物种的迭代进化，虽然突变的概率通常很低，当时它是物种进化的重要动力之一，并且这种突变不是仅仅只有一个突变点，而是有多个突变点出现在后代染色体中，当然这也是随机的，初始种群通过随机产生，对于每个个体的适应度的计算，实际上是对个体染色体编码（二进制编码）进行解码，每个基因解码后的值对应了每个项的最小支持度。根据多个基因设置各项最小支持度，之后利用修改的多最小支持度算法获得一系列为气旋强度变化项的强关联规则，利用这些规则对测试数据集进行预测，并获得预测准确度，以预测准确度作为个体的适应程度的衡量标准，计算所有个体的适应度之后，再利用遗传算子生成下一代个体，GA-MSApriori 伪代码如下所示，其中D_Train 为用于训练的事务数据集、D_Test 为用于测试的事务数据集、gene为染色体基因长度、num 为染色体基因个数、mm_sup 为各项最小支持度的最小值、min_conf 为最小置信度。

GA-MSApriori伪代码如下。

遗传算法的性能受其本身的一些参数影响，例如种群大小、如何编码、编码长度以及遗传算子中的概率等因素，GA-MSApriori 由于基于遗传算法实现，所以其性能同样也受这些因素影响，考虑到实际利用关联算法挖掘气旋关联规则时的最小支持度范围，GA-MSApriori 采用二进制对最小支持度进行编码，且编码规则如下公式：

其中init为各项最小支持度的最小阈值，bin为染色体中对应的二进制编码，将该二进制数转换为十进制数，再加上init值得到对应项的最小支持度，完成解码。

GA-MSApriori 算法中遗传算法采用最优保留策略，如式（2）所示，P为保留的最优个体，其中pk为第k 代群体的最优解f(pk)为对应的适应度，如果f(pk)>f(pk+1) ，则第k+1 代的最优个体pk+1为上一代的最优个体pk，即f(pk+1) =f(pk)，如果上一代的最优个体并不优于最新一代的最优个体，则不保留上一代最优个体，可以看出如果在某一代群体中发现了该问题的最优解，则这个解将会一直保留下去。并且规定，如果第k 代最优个体的适应度大于第k+1代的最优个体，会将第k代个体保留，并且它将同k+1 代的其它个体一起产生第k+2 代个体，相当于k+1 代在原有的基础上新增了一个个体，参与后续的种群遗传。

对每个个体的适应度计算均是要利用多关联度的Apriori算法进行关联规则挖掘，利用规则进行预测得到对应的预测准确度，该准确度即为个体的适应度。Apriori算法中有一个重要的先验性质，即频繁项集的所有子集也是频繁的，如果每个项的最小支持度是不同的，假设有A、B、C 三个项，其中最小支持度有MIS(A)>MIS(B)>MIS(C) ，2-项集{A,B}，假设有sup{A,B}min{MIS(A),MIS(B),MIS(C)}的可能，因为C 的支持度阈值最小，即Apriori 的先验性质失效，所以多支持度Apriori 首先将每个事务中的项按照最小支持度进行升序排序，即保证所有的多项集中的单个项是按照其支持度阈值大小进行排序的，并且其子集必须包含第一项，即三项集只有{C,B,A}这一种表示，且它的所有二项子集为{C,A}、{C,B}，也就是说{A，B}并不是{C,B,A}的子集，自然也就满足了Apriori 的先验性质，且{C,B,A}只能由｛C，B｝和｛C，A｝连接而成，一种特殊的情况是，如果MIS(B)=MIS(C) ，{C,B,A}与{B,C,A}相同，判断{C,B,A} 子集是否为频繁时，{B,A} 也是{C,B,A}的子集，也需要判断其是否为频繁的。

GA-MSApriori 算法运算复杂度取决于每次产生的新一代种群个数S以及种群的迭代次数G，每个个体的适应度计算时间复杂度取决于训练集的大小T，即本算法的时间复杂度为Ο(SGT)。

4 实验

实验中选取了9 个与气旋强度变化有关的监测要素，分别是VMAX，CD20，U200，REFC，T000，O500，MSLP，DTL，SHRD。在经过滑动窗口处理之后得到的记录中，每个监测要素均被离散化为6 个布尔值，表示在6h 内的变化，以及当前值所处的范围，气旋强度用当前最大海表面风（VMAX）的值来表示，本文仅考虑VMAX 在6h 后的变化情况而非它的数值，根据在6h 后，风速提高、降低5kt来反映气旋强度是加强还是减弱，如果风速没有变化则为稳定状态。当相邻两条记录的时间间隔远远超过6h，滑动窗口将直接滑过当前记录，然后再对一个窗口中的数据进行离散化，经过滑动窗口处理后新的记录条数为39332 条，其中强度变强的记录占28.9%，强度减弱的记录占25.8%，强度不变的记录占45.3%。用于预测的要素用于离散化的相关值如表2所示。

表2 要素值划分阈值

由于本文中所设计的模型仅为预测气旋强度，所以通过关联分析算法仅获得后继为气旋强度项的规则，通过对Apriori 算法加以改进，使得其支持对每个项单独设置最小支持度，且获得关联规则时，仅考虑后继为气旋强度项。本实验利用遗传算法来获得规则预测准确度最高时各个项的最小支持度。最小置信度为60%，每个项的最小支持度设置范围在4%～19%之间，所以利用4 位二进制对每一项的支持度编码，由于共有9 个预测要素，共产生54个项，所以遗传算法个体染色体为长度216的二进制数，共54个基因，设置种群规模为100，第一代个体的编码随机生成，最大种群迭代次数为50次。遗传算子包括选择，交叉和变异，其中选择算子采用轮盘法，利用规则的实际预测准确度来衡量每个个体的适应度，即当在Apriori算法中将各项的最小支持度设置为当前个体的每个基因所对应的值，从而获得规则，用这些规则进行预测得到对应的预测准确度。采用的历史数据为1982年至2016年的已经处理为事务型数据的气旋监测数据，数据共39332 条，其中1982 年至2009 年间的数据作为训练集，共29180 条数据，剩下的2010 年至2016 年间的10152条数据作为测试集。

规则获取到之后，根据每条规则的置信度进行排序，测试数据优先与置信度高的规则进行匹配，如果记录中包含了该规则先导条件中的所有项，则验证其真实的气旋强度变化与规则中的结果是否一致，若不一致则该条规则预测不准确，对比了基于动态的交叉率和变异率的GA-MSApriori 和固定动态交叉率变异率的GA-MSApriori，动态的交叉率最大值为0.9，初始交叉率为0.75，高变异率为0.003，正常变异率为0.001；固定交叉概率为0.85，固定变异概率为0.001。种群迭代过程中，每代的最优个体适应度对比如图（3）所示，其中GAMSApriori 采用最优保留策略，可以从图中明显地看出基于动态的交叉率和变异的率的GA-MSApriori 收敛速度更快，而且在迭代50 次后得到较优的结果，只考虑所有匹配规则的数据，其预测准确度为71.8%，而由于部分数据无法与所获得的规则匹配，实际准确度为66.5%。

实验中，对比了基于统一设置各项最小支持度时预测准确度和基于GA优化后的多最小支持度的预测准确度，分别对比了支持度为9%和10%时，2010至2016年的预测准确度，如图3，显然GA优化后可以明显地提升规则的预测准确度。

表3是迭代50次得到的最优解，获得规则总数为119 条，其中置信度超过65%的规则有75 条，部分规则如附录中所示，可以从规则中发现气旋强度变化的规律，例如规则：“SHRD_LO；MSLP_Decreasing；REFC_M；REFC_Stable；VMAX_Increasing；->I”，该条规则反映了若当前气旋切向量风速（SHRD）很低，海面气压（MSLP）有降低趋势，200hPa相对涡流动量通量辐合（REFC）过去变化稳定且值处于低和高之间，且气旋风速有增大趋势，则在6h 以后气旋强度增大的可能性比较大，该条规则的支持度为5.5%，置信度为73.8%，对比传统的基于关联分析的气旋强度预测模型，其输出的规律中并不包含要素的变化，例如“SHRD_LO；REFC_M；REFC_Stable；->I”，传统的预测规则中包含的信息相对较少。

表3 各项最小支持度

5 结语

气旋强度预测的重要程度不言而喻，本文提出模型首先利用滑动窗口对历史数据进行处理，尽可能发现数据中隐藏的信息，使得处理后的每条数据中不仅包含了预测变量值所处的范围，还包括了预测变量在近期的变化趋势，这意味着如果采用相同的预测变量，经过滑动窗口处理后的数据将蕴含更多的信息，这些数据有助于提高气旋强度预测的准确性。GA-MSApriori 算法获得了预测准确度最高的一系列规则，这些规则揭示了预测变量过去的变化对未来气旋强度的影响，但是在对数据进行预处理时，如何划分预测变量的变化范围仍需要进一步的深入研究，需要结合气象学的相关专业知识，使得算法的输入数据更加合理，对提高气旋强度的预测准确度有重要意义。