多要素多目标武器装备协同规划系统∗

史继筠 张 驰 连贺扬 陈杰浩 张美慧

（1.北京理工大学计算机学院 北京 100081）（2.中国工业互联网研究院 北京 100016）

1 引言

随着信息化技术的快速发展，未来战争的作战形式将会发生巨大变革。单一作战已经无法适用复杂多变战场态势，多军兵种联合作战将成为未来战场的主要作战形式［1］。为了达成联合作战目标，需要根据战场态势对武器装备进行实时协同规划。武器装备协同规划是指根据战场环境、武器及作战平台状态等多种限制元素，将指挥系统下达的作战任务通过智能决策分解至各个可调配的任务执行单元，依据火力卡片为各发射平台及保障资源制定任务准备-机动-待机隐蔽-发射-波次转换等全流程的行动规划，缩短作战单元暴露时间，降低敌方探测和打击风险。当前如遗传算法［2］、蚁群算法［3］、整数规划［4］等传统算法已经广泛应用于武器装备协同规划任务中，但是存在一定缺陷和不足。例如，遗传算法运行时间过长、容易陷入局部最优解；整数规划只能处理小规模问题；传统神经网络算法依赖于训练数据，容易受到噪声和干扰的影响，导致预测结果不准确。

随着强化学习［5］的飞速发展与应用，为武器装备的协同规划问题提出了新的解决方案。强化学习相比于传统算法更具有自主学习能力和适应性，通过选择动作与环境进行交互获得反馈，以最小化误差和代价函数为目标从而实现更加高效的决策制定。综上所述，针对当前武器装备领域协同规划问题现存缺陷，提出了一套基于强化学习的多要素多目标武器装备协同规划方案，通过基于深度强化学习的武器装备调度算法和基于注意力机制的多车辆全局路径规划算法，实现导弹发射场景下的武器装备协同控制。

2 问题描述

以导弹装备的部署发射作为主要的实验场景，导弹装备在进行发射任务之前，都会在各自的战略隐蔽点进行待命准备，当指挥系统收到导弹发射的任务和指令之后，指挥系统会根据任务需要的导弹种类、导弹数量、任务优先级等要素信息，对整个战区的战备导弹进行全局调度，赶往任务地点进行导弹发射。在这个过程中我们需要尽可能地缩短暴露时间，减少路径冲突，因此要对作战单元进行全方位的协同规划。因为整个作战场景过于复杂，优化目标多样，直接对整个问题进行建模和最优方案求解，往往使得算法无法很好收敛。因此我们对整个场景进行两阶段求解，先根据预储的导弹资源，战备位置，任务需求等要素，对战备导弹资源和导弹发射任务进行全局分配调度，再根据整体的分配情况，对所有车辆进行一个全局路径规划减少路径冲突，进而形成一整套的协同规划方案。

3 基于SAC的武器装备调度算法

本章将重点介绍武器装备调度分配阶段的算法内容。详细介绍了强化学习中状态空间、动作空间、奖励函数、决策网络模型以及算法训练过程等重要内容。

3.1 马尔可夫决策建模

3.1.1 状态空间

在基于SAC（Soft Actor Critic）［9］的集中式武器装备调度算法中，由于将整个中央决策中心当作一个智能体进行训练，因此观测到的状态空间应该是包括全局所有武器装备状态以及目标任务等状态的空间。那么通过上文问题定义可以确定，整个状态空间由三部分组成其中，Otc表示所有武器装备的相关状态信息，Otr表示所有目标任务的相关状态信息，Ot d表示所以资源补给点的相关状态信息。对于单个武器装备所具有的属性包括：经度属性，维度属性，携带资源分布属性，发射成功率属性，剩余油储量；对于单个目标任务所具有的属性包括：经度属性，维度属性，需求资源分布属性，任务的重要程度；最后是资源补给点的相关属性主要包括经度属性和维度属性。

3.1.2 动作空间

首先，对于一个武器装备执行单元来说，能够进行方案选择有：任务出派、隐蔽待敌、资源补给。而任务出派的目标则有m个任务目标可以选择，资源补给也有k个资源补给点可以选择，再加上原地隐蔽待敌，因此总共有m+k+1 中选择，因此对于一个武器装备来说其动作空间是一个大小为m+k+1 的离散动作空间。其次，由于本算法是将整个中央决策系统当作一整个智能体，其输出应该是全局武器装备的整体决策方案，因此对于N个武器装备来说，中央决策中心智能体的动作选择空间应该是一个多维离散动作空间，其表示如式（1）所示：

3.1.3 奖励函数

最后一部分是方案分配的最大距离惩罚q如式（4）所示，表示的是方案分配中最远的武器装备到目标地点的距离，这个指标影响着整个方案的最终响应时间。

因此，最终的一个单步奖励rt如式（5）所示，其中α,ω为超参数，用于平衡各个奖励目标和惩罚目标之间的权重。

3.2 Actor-Critic模型设计

该算法的神经网络结构主要有两个分别是Q-Critic网络和Actor策略网络。在该网络结构中，Actor 网络和Q-Critic 网路共用一个状态特征提取层。特征提取层操作很简单，将执行单元和任务单元分别进行一个线性变化获得基础编码，再将整个状态编码展开为一个一维向量，在多要素多目标武器装备调度问题中，其输出是一个15360 维的一维向量。整体结构如下图1所示。

图1 网络结构图

3.3 SAC算法训练

SAC 算法训练过程中，首先初始化并设置策略网络、Q 网络和目标函数网络参数。为了增强训练效果，引入熵［10］正则化项鼓励策略保持多样性，避免局部最优问题，同时使用自适应温度参数平衡探索和利用。在收集样本阶段，使用当前策略从环境中收集经验样本，并存储到回放缓冲器中。在训练过程中，随机抽取并重要性采样样本来更新策略网络和Q网络，并可以动态调整学习率。策略迁移可在学习到的策略网络上探索新状态并继续训练。训练会在达到预设的停止条件时停止。

4 基于注意力机制的全局路径规划算法

本章介绍了基于注意力机制［6］的全局路径规划算法的设计过程，包括奖励函数、多头注意力模型、贪婪滚动基线训练等各个强化学习训练模块。

4.1 马尔可夫决策建模

4.1.1 状态空间

在这个全局路径规划问题中，状态空间由三部分组成：全局节点集合状态、多车辆初始节点状态、当前所在节点状态、目标节点状态。具体表现如式（6）所示，其中vN={v1,v2,v3…,vN}表示整个战场道路网络分布及路口车流量特征，vM={v1,v2,v3…,vM}表示所以执行单元初始位置分布特征，vi表示当前规划路径的车辆起始节点i，vj表示当前规划路径的车辆目标地节点j。

4.1.2 动作空间

在路径规划问题中常用地图节点集合当作动作空间，这种方式被称为节点选择问题。这种节点选择问题的动作空间，因为节点的数量很大，在进行动作选择时，通过还需要屏蔽机制（Mask），限制节点的数量，以确保智能体只能选择与当前节点存在地图道路的下一个节点。通过不断地选择下一个节点，最终就能形成由一组地图节点所组成的行驶路径。

4.1.3 奖励函数

奖励函数用于评估代理执行一个动作的好坏。在路径规划问题中，为了找到最短路径，可以定义奖励函数为选择的节点到当前节点路径长度的相反数。同时通过设置一个惩罚因子，对智能体选择过于拥挤的节点进行惩罚，来指导智能体做出更好的决策。具体的奖励函数表示如式（8）所示：

rt=-path_length-penalty*invalid_action（8）

其中，patℎ_lengtℎ 表示路径长度，penalty是一个惩罚因子，用于惩罚智能体选择拥挤的节点，惩罚因子的大小随着拥挤程度的提升而提升，而invalid_action是一个指示函数，如果智能体选择的节点不符合要求，则为1，否则为0。

4.2 注意力模型设计

本章方法的模型结构源于传统的Encoder-Decoder 结构。在这个路劲规划问题中，每一个输入Xi都是一个维度为2 的向量。编码器首先会通过一个线性变化将每个xi编码为维度是128 的特征向量（node embeding），表示为ℎ0i。接着会经过一个循环N层的网络结构，每一层里面都由一个多头注意力机制层（multi-head attention）和一个前馈反馈层（feed forward）两个子层组成，每一个子层会经过一个残差网络［7］进行传播，其结构如图2所示。

图2 编码器结构

解码器结构主要由两个部分组成，一部分同样是一个多头注意力机制，用于将解码器输出的图特征编码以及其他特征进行融合，变成一个整体上下文特征编码。接着是另一部分，是一个基于单注意力机制的概率计算层，通过计算每个节点对上一层输出的上下文特征编码的重要程度，再将其转化为概率值。根据概率值，就可以根据不同的策略来选取下一个节点，重复多次这个过程，就可以得到智能体的路径规划。具体的解码器结构如图3所示。

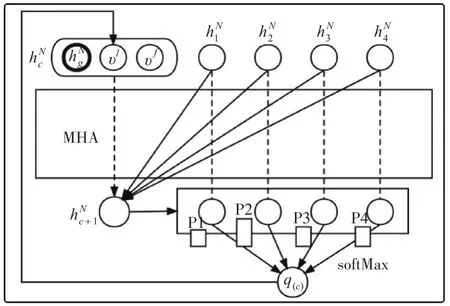
图3 解码器结构

4.3 REINFORCE算法训练

模型采用REINFORCE［8］算法训练，同时采用贪恋基线进行更新。该思想参考了DQN 算法中Target 网络的思想。创建两个结构完全一样的网络，一套拥有最新的参数，一套则固定为老的参数。在每个epoch 结束后，对比两个当前策略和基线策略的结果，如果当前策略的累计奖励期望比基线策略有显著的提升时，将当前策略参数复制给基线策略，以此不断提升当前策略网络的效果。

5 实验

5.1 实验设计

为了验证算法的有效性和先进性，我们进行了以下三个方面的实验设置：环境设置、武器装备调度实验、全局路径规划实验。

5.1.1 实验环境

本课题采用PyCharm 作为开发工具，使用的语言为python3.9，采用了pytorch 深度学习框架构建深度强化学习网络。实验的运行环境及软硬件配置如表1所示。

表1 实验运行环境及软硬件设置

5.1.2 仿真环境

本节针对武器装备调度问题和多车辆路径规划问题，构建战场仿真环境以便训练DRL 算法。整个仿真环境是城市地理环境，以广州大学为中心，作战区域为8000km2，其中北纬23.0985 以北为备战区域，北纬22.0575 以南为发射区域。本实验包含三个不同规模的仿真环境：env20、env50、env100。env20 为20 个执行单元和4 个任务单元，env50为50个执行单元和10个任务单元，env100为100 个执行单元和20 个任务单元。其他仿真环境的参数如表2所示。

表2 仿真环境参数设置

5.2 武器装备调度实验

5.2.1 评价指标

本小节重点介绍在多要素多目标武器装备调度实验中用到的性能评价指标如表3 所示。这些指标由合作单位某航天研究院提供，通过任务完成度表示战备资源分配效果；最大行驶距离和平均行驶距离表示部队响应速度；算法时间复杂度表示部队调度的实时性和敏捷性。

表3 武器装备调度实验评价指标

5.2.2 收敛性实验

本节所有的实验结果是基于上一小节中env100的环境进行训练，具体的累计奖励曲线和损失曲线如图4 所示。从累计奖励曲线可以看出算法在60000 步的时候开始进入稳定期，算法开始收敛，最终每轮训练的平均累计奖励稳定在80 上下（理论累计奖励最大值为200）。这些实验结果说明该算法最终都能够成功收敛。

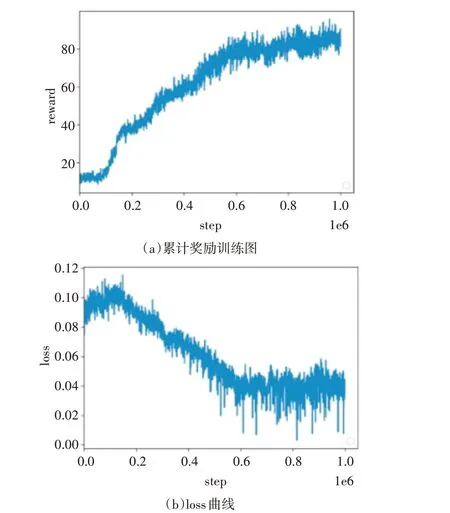
图4 基于SAC的武器装备调度算法结果图

5.2.3 对比试验

对于多要素多目标武器装备调度问题，其主要的评价指标有四个，分别是：任务完成度、最大行驶距离、平均行驶距离和以及算法时间复杂度。进行对比的算法有四种：随机选择、贪心算法、最优强化学习算法、遗传算法。其中随机选择算法通过完全随机的方式生成决策方案，这个算法作为基础参照指标。贪心算法则是对任务进行重要程度排序，优先完成重要程度高的任务，同时对执行单元的距离进行排序，优先调度最近的执行单元前去完成任务。最优强化学习算法，则是调度算法经过调参训练后的最优模型。遗传算法则是根据遗传规律，以启发式搜索的形式在解空间中搜索出一个相对最优解。最终这四种算法关于四个指标在不同规模数据集上的表现如图5 所示。从结果可以看出，随着问题规模的增加，该调度算法在任务完成度、算法时间复杂度上的优势越来越明显。同时在最长行驶距离和平均行驶距离与贪心算法的差距也在不断变小。

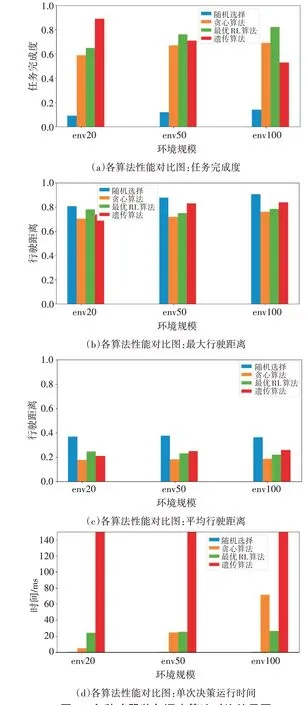
图5 多种武器装备调度算法对比结果图

在任务完成度方面，因为在问题规模较小的时候，遗传搜索算法能够在较小的解空间中找出优秀的解，但随着问题规模增大，在有限时间内搜索出一个优秀解就越来越困难，而强化学习基于概率的特性在数据规模大的时候就逐渐显现出优势。在路径长度方面，贪心算法以最短路径为贪心目标，所以在路径方面具备优势，强化学习算法则更具综合优势。在算法时间复杂度，其他算法随着问题规模的增长而增长，但强化学习则基本稳定不变。

5.3 全局路径规划实验

5.3.1 评价指标

本节重点介绍在多车辆全局路径规划实验中用到的性能评价指标。路径冲突次数、最大行驶时间、平均行驶时间、算法时间复杂度指标将在对比试验作为主要的对比指标，证明所提出算法的先进性。这些指标同样由合作单位给出，路径冲突次数表示全局规划的平衡性；最大行驶时间和平均行驶时间表示路径规划的先进性；算法时间复杂度表示规划的实时性和敏捷性。具体介绍如表4所示。

表4 全局路径规划实验评价指标

5.3.2 收敛性实验

本节所有的实验结果是基于上一小节中env100的环境进行训练，具体的累计奖励曲线和损失曲线如图6 所示。因为路径规划中奖励函数都是惩罚机制，最终的结果是最小化惩罚，所以平均累计奖励为负值。从实验结果可以看到最终在500000 步的时候，累计奖励稳定到了-60 的位置，证明了该算法最终可以成功收敛。

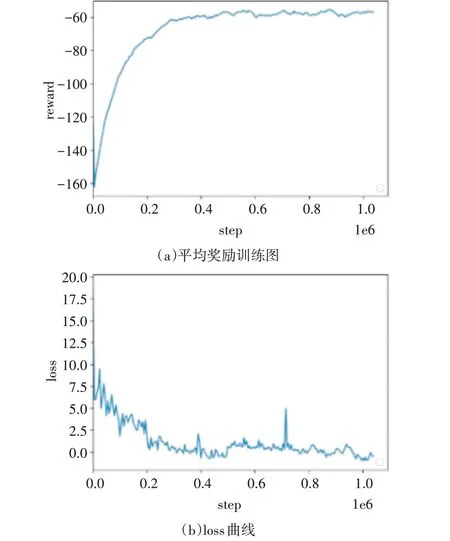
图6 基于注意力机制的全局路径规划算法结果图

5.3.3 对比试验

对于全局多车辆路径规划问题，其主要的评价指标有四个，分别是：平均行驶时间、最长行驶时间按、路径冲突次数、算法时间复杂度。进行对比的算法有两种：注意力模型、Dijkstra。其中注意力模型算法是基于注意力模型的路径规划算法；Dijkstra 是单源最短路径算法。最终这两种算法关于四个指标在不同规模数据集上的表现如图7 所示。整体来看，随着问题规模的增加，Dijkstra 算法的路径冲突次数急剧上升，导致，进而导致行驶时间急剧上升，表现越来越差。而基于注意力机制的路径规划算法则表现越来越好，且在算法时间复杂度上，也优于传统算法。

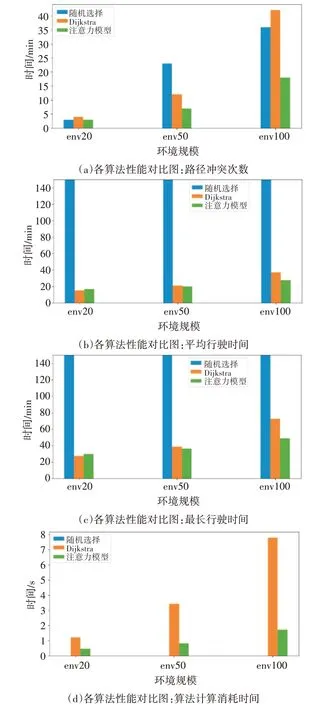
图7 多种全局路径规划算法对比结果图

6 结语

该研究通过强化学习的方法设计了一套多要素多目标武器装备协同规划算法。希望通过协同规划算法能够辅助我军指挥官更好的进行科学有效的规划决策，适应信息化联合作战趋势。研究将该问题分解为了两个子问题：多要素多目标武器装备调度问题和多车辆全局路径规划问题。并针对两个阶段的问题分别提出了基于SAC 的武器装备调度算法和基于注意力机制的全局路径规划算法。最后通过和传统算法的对比试验，证明了提出方法的有效性和先进性。这项研究为武器装备协同规划问题提供了新的思路和解决方案，也为算法的优化和改进提供了有益的参考。相信这些算法的思路有很大的潜力在未来的应用中会继续得到完善和发展。