研高考真题 思教材习题 提核心素养——以2023年新课标Ⅱ卷第21题为例

张小美

(山东省威海市文登区南海高级中学)

解析几何是高中数学的重要内容,而直线与圆锥曲线的位置关系是解析几何的核心,也是高考大题必考的内容之一.《普通高中数学课程标准(2017年版)》对解析几何的要求:根据几何问题和图形的特点,用代数语言把几何问题转化成为代数问题;根据对几何问题的分析,探索解决问题的思路;运用代数方法得到结论;给出代数结论合理的几何解释,解决几何问题.代数的方法即方程的思想——联立、求根的判别式、再利用韦达定理求解,在运用代数方法解决问题的同时,提升学生直观想象、数学运算、数学建模、逻辑推理和数学抽象的核心素养.

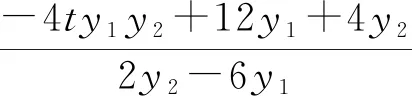
(1)求C的方程;

(2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于点P.证明:点P在定直线上.

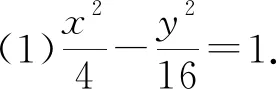
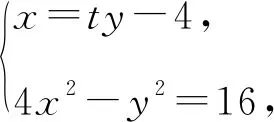
【方法一】将y1y2转化成y1+y2

观察韦达定理,我们不难发现

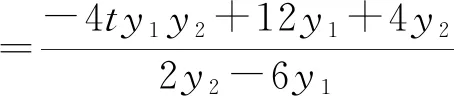
所以交点P在定直线x=-1上.

【注】该方法的难点在于寻找y1y2与y1+y2的关系.

【方法二】y1,y2只保留一个

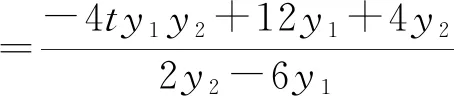
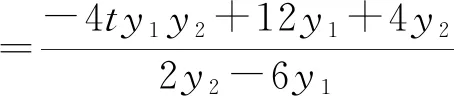
【注】该方法分子与分母保留的变量必须一致,否则达不到化简的目的.

【方法三】试探出定值

【注】利用“对称型韦达定理”待定出参数λ的值之后,勿忘检验.

【方法四】暴力求根

所以x0=-1.

【注】该方法易想,但计算量相对较大.

纵观“非对称韦达定理”的四种处理方法:方法一与二是我们最常用的方法;方法三先猜出定值然后再验证也是不错的选择;方法四是初学者遇到这类问题首想的方法,但是缺点显而易见.不论哪一种方法,其实对学生的数学运算能力都有很高的要求.如何避开这种算法,寻找一种相对简便的算法?我们先来看一道教材习题.

(人教B版选择性必修第一册P149习题2-6C)

1.如果过点(6,0)的直线与过点(-6,0)的直线相交于点M,而且两直线斜率的乘积为a,其中a≠0.

(1)求点M的轨迹方程;

(2)讨论M的轨迹是何种曲线.

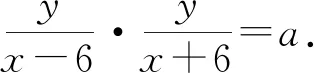
(2)当a>0时,轨迹为除去(6,0),(-6,0)两点的双曲线;

当a<0且a≠-1时,轨迹为除去(6,0),(-6,0)两点的椭圆;

当a=-1时,轨迹为除去(6,0),(-6,0)两点的圆.

将定点(±6,0)一般化,就得到了椭圆、双曲线的第三定义:如果过点A1(-a,0),a>0的直线与过点A2(a,0)的直线相交于点M,而且两直线斜率的乘积为n,其中n≠0,则M的轨迹为:

当n>0时,轨迹为除去A1,A2两点的双曲线;

当n<0且n≠-1时,轨迹为除去A1,A2两点的椭圆;

当n=-1时,轨迹为除去A1,A2两点的圆.

我们不妨大胆设想一下,既然斜率之积为定值的点的轨迹可求,那么斜率之比为定值的点的轨迹又是什么呢?

问题：如果过点A1(-a,0),a>0的直线与过点A2(a,0)的直线相交于点M,而且过A1的直线斜率与过A2的直线斜率之比为n,其中n≠0,求M点轨迹.

因此,我们可以得到一个更为一般的结论.

结论：如果过点A1(-a,0),a>0的直线与过点A2(a,0)的直线相交于点M,而且过A1的直线斜率与过A2的直线斜率之比为n,其中n≠0,则M点轨迹是垂直于x轴的两条射线.

由上述结论,回归真题,除了常规解法,还可以另辟蹊径:因为直线MN过定点,由轴点弦定理知直线A1M与直线A1N的斜率之积为定值.而由双曲线第三定义知,直线A1N与直线A2N的斜率之积亦为定值,所以直线A1M与直线A2N的斜率之比为定值,所以P点在垂直x轴的直线上.

第一步:齐次化方法证明kA1M·kA1N为定值.

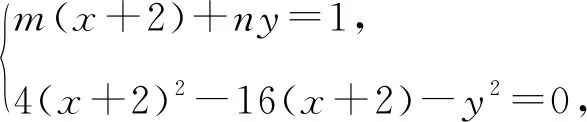
第二步:证明kA1N·kA2N为定值.

整理可得:x=-1.

第二种算法避开了烦琐的“非对称韦达定理”,计算相对简捷.但需要学生先分析题目的几何特征,搞清多条直线间的斜率关系,才能快速找到本题的入手点.这个过程提升了学生的数学抽象、逻辑推理以及数学运算等核心素养.

绝大多数学生、家长包括老师对数学核心素养之一的数学运算的理解仅限于算.其实,数学运算包含很多方面:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等.对同一个运算对象,如何快速地选择较为便捷的算法,教师在平时的复习备考中可以从以下两点入手.

1.教师示范算.尤其是高三一轮复习时,教师一定要重视板书.讲解运算时,一定先引导着学生观察运算对象的结构特点来理解运算.比如教材在推导椭圆的标准方程时,学生想到的方法就是移项平方,计算量不小.我们可以引导学生思考:遇到两个根号相加的结构,可以联想到哪种方法来处理?学生很容易就想到了有理化的方法,但是学生在处理的过程中会忽视分母为零的情况.此时,教师的示范算就显得尤为重要,通过板书找到学生思维的漏洞.这时有些学生会想到补救措施:既然分子有理化时有分母不等于零的限制,那在有理化的时候通过等式两边同时乘两个根号相减就没有分母不等于零的限制了.通过示范算,强化学生的结构意识,同时引发学生的思考,提高学生的数学运算、逻辑推理等核心素养.

2.学生展示算.当一轮复习帮助学生养成了良好的运算习惯,二轮复习就开始展示学生的步骤.通过展示优秀算,让其他同学发现自己的不足;通过展示问题算,让其他同学发现运算中的不规范之处,加深学生对数学运算的理解.

“题在书外,根在书中”.近几年的高考试题虽然千变万化,但是每套都能找到教材习题的影子.我们在教学时一定立足教材,深挖教材的内涵与外延.只有这样,才能决胜高考.